Шпора по линалу и ангему. Семестр 1. Матрицы действия с матрицами
 Скачать 249.59 Kb. Скачать 249.59 Kb.
|
|
МАТРИЦЫ Действия с матрицами Умножение на число, сложение, вычитание, транспонирование, умножение 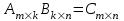 Свойства 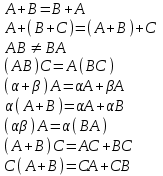 2. ОПРЕДЕЛИТЕЛИ Алгебраические дополнения и миноры Минор  квадратной матрицы А – определитель матрицы, полученной из матрицы А вычёркиванием i-й строки и j-го столбца. квадратной матрицы А – определитель матрицы, полученной из матрицы А вычёркиванием i-й строки и j-го столбца.Алгебраическое дополнение 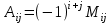 Свойства определителей ∆ транспонированной матрицы = ∆ исходной матрицы Если поменять местами 2 строки/столбца, ∆ изменит знак Если ∆ содержит 2 одинаковые строки/столбца, то ∆=0 Если ∆ содержит нулевую строку/столбец, то ∆=0 Общий множитель в строке/столбце можно выносить за знак определителя ∆ не изменится, если к любой строке/столбцу прибавить (вычесть) любую другую строку/столбец, умноженную на любое число ОБРАТНАЯ МАТРИЦА ∆≠0→матрица невырожденная Для всякой невырожденной матрицы существует обратная матрица Свойства  СЛАУ Система Совместная – имеет хотя бы 1 решение Несовметная – не имеет решений Определённая – имеет единственное решение Однородная – все свободные члены = 0 Неоднородная – есть свободные члены ≠ 0 Метод Крамера Число уравнений = числу переменных 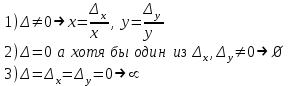 Ранг матрицы – наибольший из порядков миноров данной матрицы, отличный от нуля. Теорема о базисном миноре: базисные строки/столбцы линейно независимы; любая строка/столбец матрицы А является линейной комбинацией базисных строк/столбцов. Условия совместности СЛАУ: Ранг основной матрицы < числа неизвестных: r < n ∆ = 0 СИСТЕМЫ КООРДИНАТ Декартовы Полярные 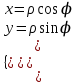 Цилиндрические  Сферические  ПОЛЯРНЫЕ КООРДИНАТЫ  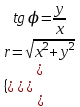 ПЛОЩАДЬ ТРЕУГОЛЬНИКА  6. ВЕКТОРЫ НА ПЛОСКОСТИ Линейная комбинация векторов  - вектор - вектор 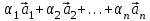 , где , где  - числа - числаЛинейно зависимые  , не все , не все  =0 =0Линейно независимые  , все , все  =0 =0Базис в пространстве – любая упорядоченная тройка некомпланарных векторов. Направляющие косинусы   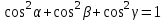 Критерий коллинеарности векторов 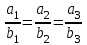 Деление отрезка в данном соотношении λ  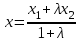 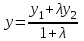 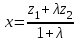 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 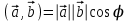 Свойства 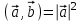   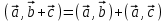 Угол между векторами 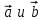 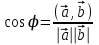 Проекция вектора на ось 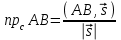  Условие ортогональности векторов  ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ  Свойства  Вычисление векторного произведения  Условие коллинеарности векторов 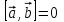 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ  = =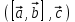 Свойства  = =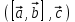 = =  = =  = =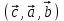 = = = =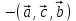 = =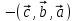  Правая тройка→  > 0 > 0Левая тройка→  < 0 < 0Вычисление смешанного произведения  Условие компланарности векторов  =0 =0ДВОЙНОЕ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ  КОМПЛЕКСНЫЕ ЧИСЛА Алгебраическая форма комплексных чисел 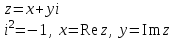 Тригонометрическая форма комплексных чисел 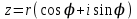 Показательная форма комплексных чисел 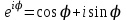 → →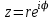 Степень комплексного числа 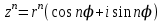 Корень n-ной степени из комплексного числа 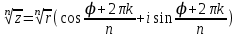 11. ПЛОСКОСТЬ Общее уравнение плоскости   - нормаль - нормаль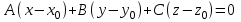 Уравнение плоскости в отрезках  Нормальное уравнение плоскости  Нормирующий множитель 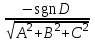 Расстояние от точки до плоскости 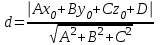 Уравнение плоскости, проходящей через 3 точки 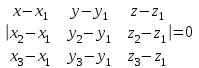 Взаимное расположение плоскостей Совпадают: 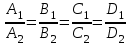 Параллельны:  Перпендикулярны:  Угол между 2 плоскостями 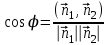 12. ПРЯМАЯ В ПРОСТРАНСТВЕ Канонические уравнения прямой   - направляющий - направляющийПараметрические уравнения прямой  Прямая как линия пересечения 2-х плоскостей 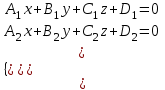 Взаимное расположение прямой и плоскости Подставим в уравнение плоскости  значения x, y, z из уравнения прямой значения x, y, z из уравнения прямой 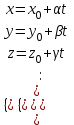  Угол между прямой и плоскостью 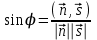 где где  - нормаль плоскости, - нормаль плоскости,  - направляющий вектор прямой - направляющий вектор прямойРасстояние от точки до прямой 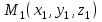   Взаимное расположение прямых :  Точка пересечения двух прямых: Точка пересечения двух прямых: Или   Угол между 2 прямыми  13. ПРЯМАЯ НА ПЛОСКОСТИ Виды уравнений прямой на плоскости Общее  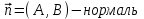 Каноническое 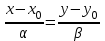 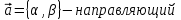 Параметрическое 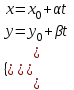 С угловым коэффициентом 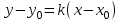   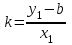 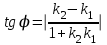 - угол между прямыми - угол между прямымиВ отрезках  Нормальное  Нормирующий множитель  В полярной системе координат 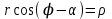 Взаимное расположение прямых на плоскости 1)совпадают:  2)параллельны:  3)перпендикулярны:  4)пересекаются: 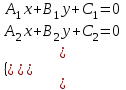 Уравнение прямой проходящей через 2 данные точки 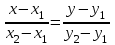 Расстояние от точки до прямой 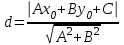 Угол между 2 прямыми на плоскости 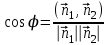 14. Кривые второго порядка 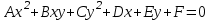 Вырожденные кривые: пустое множество, точка, прямая, пара прямых. Невырожденные кривые: эллипс, гипербола, парабола. Эллипс – ГМТ точек М на плоскости, сумма расстояний от которых до двух фиксированных точек  и и 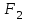 есть постоянная величина 2а, превышающая расстояние между фокусами 2с: есть постоянная величина 2а, превышающая расстояние между фокусами 2с: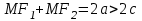  Эксцентриситет  величина, характеризующая меру сжатия эллипса, величина, характеризующая меру сжатия эллипса, 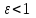 Директрисы 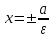 Отношение расстояния r от точки эллипса до фокуса к расстоянию d до ближайшей к этому фокусу директрисы равно эксцентриситету:  Оптическое свойство: лучи света, вышедшие из одного фокуса эллипса, после отражения от эллипса соберутся в другом фокусе. Гипербола – ГМТ М на плоскости, модуль расстояний от которых до двух фиксированных точек  и и 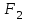 есть постоянная величина 2а, меньшая расстояния между фокусами 2с: есть постоянная величина 2а, меньшая расстояния между фокусами 2с: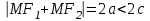  Эксцентриситет  для гиперболы для гиперболы  Директрисы 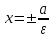 Прямая называется асимптотой гиперболы, если расстояние от точки М(х,у) гиперболы до этой прямой стремится к 0 при х → ± бесконечность. Асимптоты гиперболы  Отношение расстояния r от точки гиперболы до фокуса к расстоянию d до ближайшей к этому фокусу директрисы равно эксцентриситету:  Оптическое свойство: лучи света, вышедшие из одного фокуса гиперболы, после отражения от ближайшей ветви гиперболы распространяются так, будто вышли из другого фокуса. Парабола – ГМТ плоскости, равноудалённых от фиксированной точки плоскости (фокуса) и фиксированной прямой плоскости (директрисы). 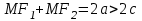 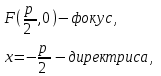  p-параметр параболы p-параметр параболыОптическое свойство: лучи света, вышедшие из фокуса параболы, после отражения от параболыпараллельны оси параболы. 15. ПРЕОБРАЗОВАНИЯ КООРДИНАТ Параллельный перенос   Поворот осей координат 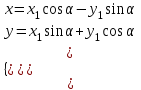  17. ИНВАРИАНТЫ КРИВЫХ ВТОРОГО ПОРЯДКА     , , 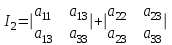 Если 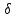 > 0, > 0,  < 0 → эллипс < 0 → эллипсЕсли 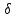 > 0, > 0,  > 0 → мнимый эллипс > 0 → мнимый эллипсЕсли 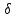 > 0, ∆ = 0 → пара мнимых пересекающихся прямых > 0, ∆ = 0 → пара мнимых пересекающихся прямыхЕсли 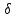 < 0, ∆ ≠ 0 → гипербола < 0, ∆ ≠ 0 → гиперболаЕсли 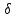 < 0, ∆ = 0 → пара пересекающихся прямых < 0, ∆ = 0 → пара пересекающихся прямыхЕсли 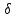 = 0, ∆ ≠ 0 → парабола = 0, ∆ ≠ 0 → параболаЕсли 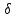 = ∆ = 0, = ∆ = 0,  < 0 → пара параллельных прямых < 0 → пара параллельных прямыхЕсли 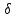 = ∆ = 0, = ∆ = 0,  > 0 → пара мнимых параллельных прямых > 0 → пара мнимых параллельных прямыхЕсли 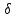 = ∆ = = ∆ =  = 0 → пара совпавших прямых = 0 → пара совпавших прямых18. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 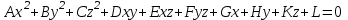 Вырожденные поверхности: пустое множество, точка, прямая, плоскость, пара плоскостей Невырожденные поверхности: Сфера   Эллипсоид 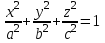 Однополостный гиперболоид  Двуполостный гиперболоид  Конус второго порядка  Эллиптический параболоид 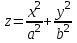 Гиперболический параболоид 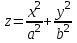 Эллиптический цилиндр  Гиперболический цилиндр  Параболический цилиндр  Метод сечений z=h, x/y=h
19. ЛИНЕЙНЫЕ ПРОСТРАНСТВА Множество R элементов x, y, z … любой природы называется линейным (аффинным) пространством, если выполнены следующие три требования: 1.Имеется правило, посредством которого любым двум элементам этого пространства х и у ставится в соответствие третий элемент, называемый суммой этих элементов. 2.Имеется правило, посредством которого любому элементу х множества R и любому вещественному числу λ cтавится в соответствие элемент u этого множества, называемый произведением элемента х на число λ. 3.Указанные правила подчинены восьми аксиомам:  Свойства 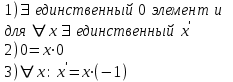 ЕВКЛИДОВЫ ПРОСТРАНСТВА Вещественное линейное пространство R называется вещественным евклидовым пространством, если выполнены следующие два требования: Имеется правило, посредством которого любым двум элементам этого пространства х и у ставится в соответствие вещественное число, называемое скалярным произведением этих элементов. Указанные правила подчинены четырём аксиомам: 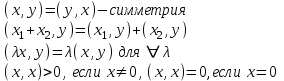 Свойства:  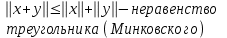 |
