физон. Истоком и стоком тока соответственно. Такая двухполюсная система в проводящей среде, состоящая из истока и стока тока, называется
 Скачать 0.83 Mb.
|
|
1  2 Любой источник тока обладает своим сопротивлением  , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.Пусть источник тока с ЭДС, равной  , и внутренним сопротивлением подключён к резистору  (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).3.Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС. На рис. 3 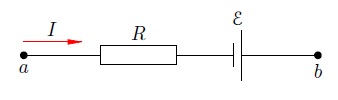и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор  ). Рис. 3. ЭДС «помогает» току:  Сила тока на участке равна  , ток течёт от точки  к точке  . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.Пусть потенциалы точек и равны соответственно  и  . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.Напряжение на нашем участке равно:  . За время  через участок проходит заряд  , при этом стационарное электрическое поле совершает работу: Кроме того, положительную работу совершает источник тока (ведь заряд  прошёл сквозь него!): Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло:  .Подставляем сюда выражения для  ,  и закон Джоуля–Ленца: Сокращая на  , получаем закон Ома для неоднородного участка цепи: (6)или, что то же самое:  (7)Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .Отметим два следствия выведенных формул (6) и (7). 1. Если участок однородный, то  . Тогда из формулы (6) получаем  — закон Ома для однородного участка цепи.2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на : Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что  и предыдущая формула превратится в закон Ома для полной цепи: Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка. Может быть и другой случай подключения, когда источник 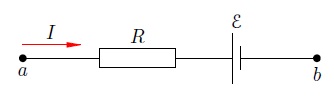«мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника. Рис. 4. ЭДС «мешает» току:  Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной: Тогда закон Ома для неоднородного участка примет вид:  (8)или:  где по-прежнему — напряжение на участке.Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:  Ток при этом течёт от точки 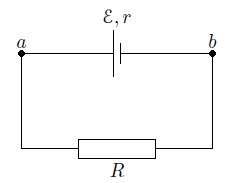к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус». Рис. 2. Полная цепь Наша задача — найти силу тока в цепи и напряжение  на резисторе .За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу: (2)Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца: (3)Итак,  , и мы приравниваем правые части формул (2) и (3): После сокращения на получаем: Вот мы и нашли ток в цепи:  (4)Формула (4) называется законом Ома для полной цепи. Если соединить клеммы источника проводом пренебрежимо малого сопротивления  , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания: Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки. Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи: (5)Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.Мы видим из формулы (5), что в реальной цепи будет  — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда  .1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При  формула (5) даёт .2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико:  . Тогда величина неотличима от , и формула (5) снова даёт нам .Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.  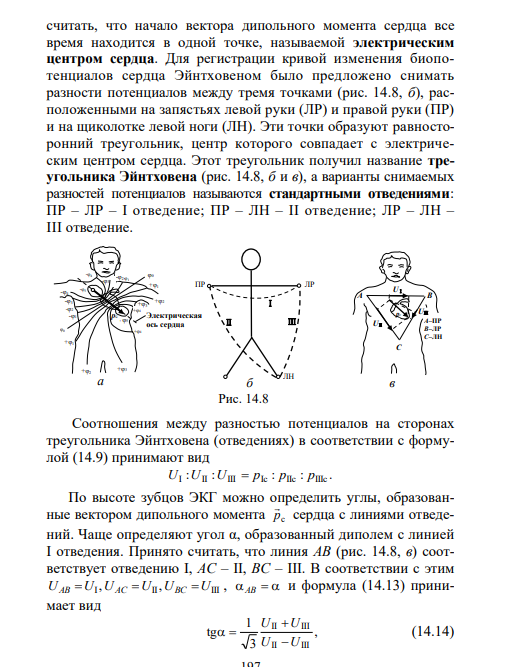  4 . Диполь является частным случаем системы электрических зарядов, обладающих определенной симметрией. Общее название подобных распределений зарядов – электрические мультиполя (I = 0, 1, 2 и т. д.), число зарядов мультиполя определяется выражением 21. Так, мультиполем нулевого порядка (20 = 1) является одиночный точечный заряд, мультиполем первого порядка (21 = 2) – диполь, мультиполем второго порядка (22 = 4) – квадруполь, мультиполем третьего порядка (23 = 8) – октуполь и т. д. Потенциал поля мультиполя убывает на значительных расстояниях от него (R > d, где d – размеры мультиполя) пропорционально I/R1+1. Если заряд распределен в некоторой области пространства, то потенциал электрического поля вне системы зарядов можно представить в виде некоторого приближенного ряда: 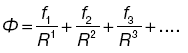 Здесь R – расстояние от системы зарядов до точки А с потенциалом Ф; f1, f2, f3…. – некоторые функции, зависящие от вида мультиполя, его заряда и от направления на точку А. Первое слагаемое соответствует монополю, второе – диполю, третье – квадруполю и т. д. В случае нейтральной системы зарядов первое слагаемое равно нулю. Дипольный электрический генератор (токовый диполь) В вакууме или в идеальном изоляторе электрический диполь может сохраняться сколь угодно долго. Однако в реальной ситуации (электропроводной среде) под действием электрического поля диполя возникает движение свободных зарядов, и диполь нейтра-лизуется. Сила тока во внешней цепи будет оставаться почти постоянной, она почти не зависит от свойств среды. Такая двухполюсная система, состоящая из истока и стока тока, называется дипольным электрическим генератором, или токовым диполем. |