ЭЛЕКТРИЧЕСКИЙ ТОК И ЕГО ХАРАКТЕРСТИКИ Электрическим током называют упорядоченное движение заряженных частиц или заряженных макроскопических тел. Различают два вида электрических токов – токи проводимости и конвекционные токи.
Током проводимости называют упорядоченное движение в веществе или вакууме свободных заряженных частиц .Этот ток обусловлен тем, что в проводнике под действием приложенного электрического поля напряженностью 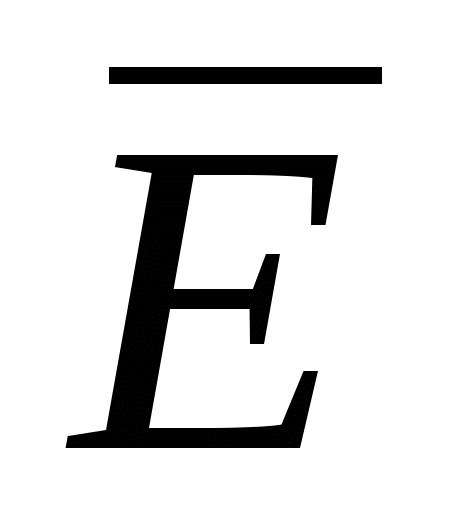 происходит перемещение свободных электрических зарядов.
происходит перемещение свободных электрических зарядов.
Конвекционным электрическим током называют ток, обусловленный перемещением в пространстве заряженного макроскопического тела.
Для возникновения и поддержания электрического тока проводимости необходимы следующие условия:1) наличие свободных носителей тока (свободных зарядов);2) наличие электрического поля, создающего упорядоченное движение свободных зарядов;
3) на свободные заряды, помимо кулоновских сил, должны действовать сторонние силы неэлектрической природы; эти силы создаются различными источниками тока (гальваническими элементами, аккумуляторами, электрическими генераторами и др.);
4) цепь электрического тока должна быть замкнутой.
За направление электрического тока условно принимают направление движения положительных зарядов, образующих этот ток.
Количественной мерой электрического тока является сила тока I - скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение Sпроводника в единицу времени: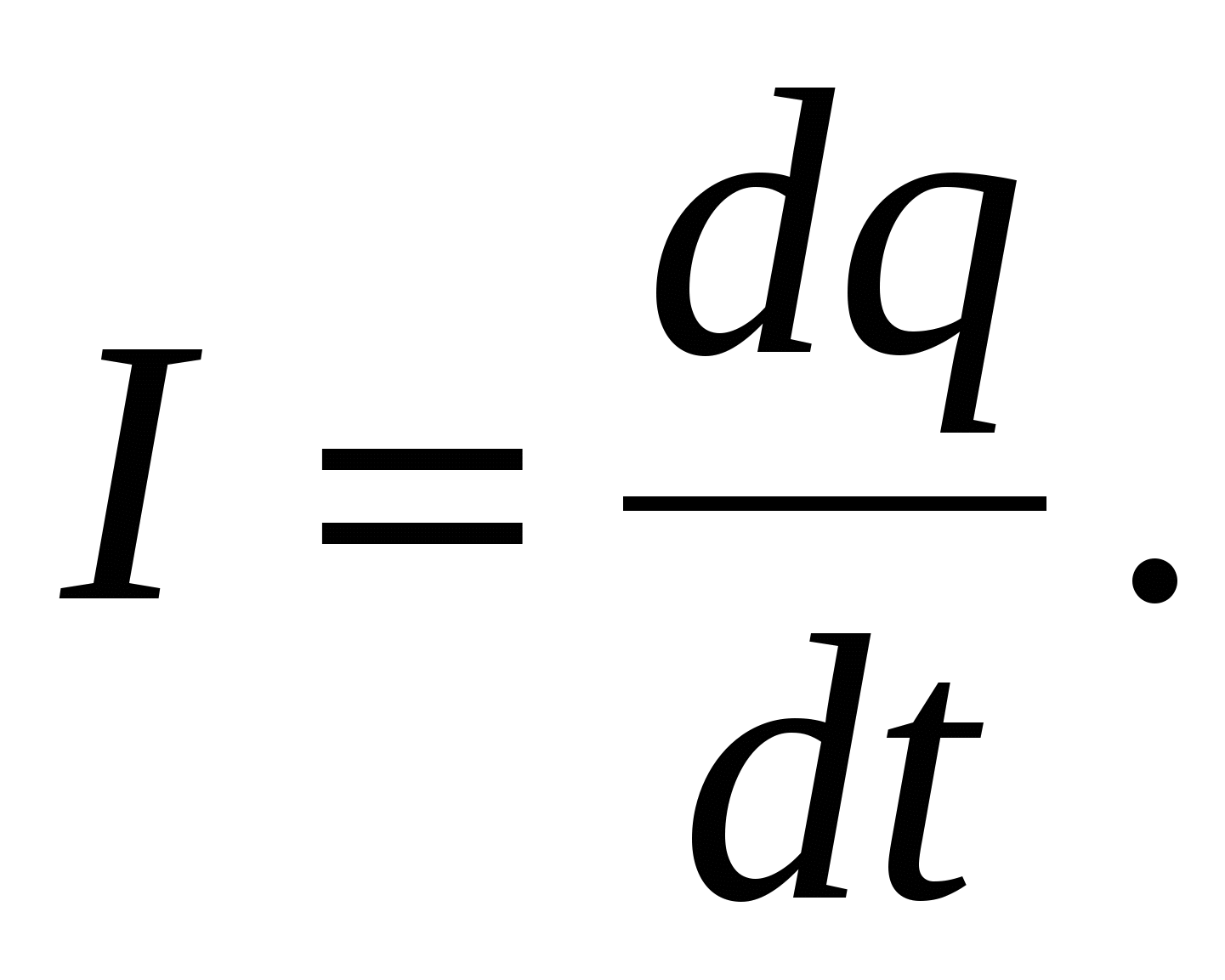 (2.1)Ток, сила и направление которого не изменяются с течением времени, называется постоянным. Для постоянного тока
(2.1)Ток, сила и направление которого не изменяются с течением времени, называется постоянным. Для постоянного тока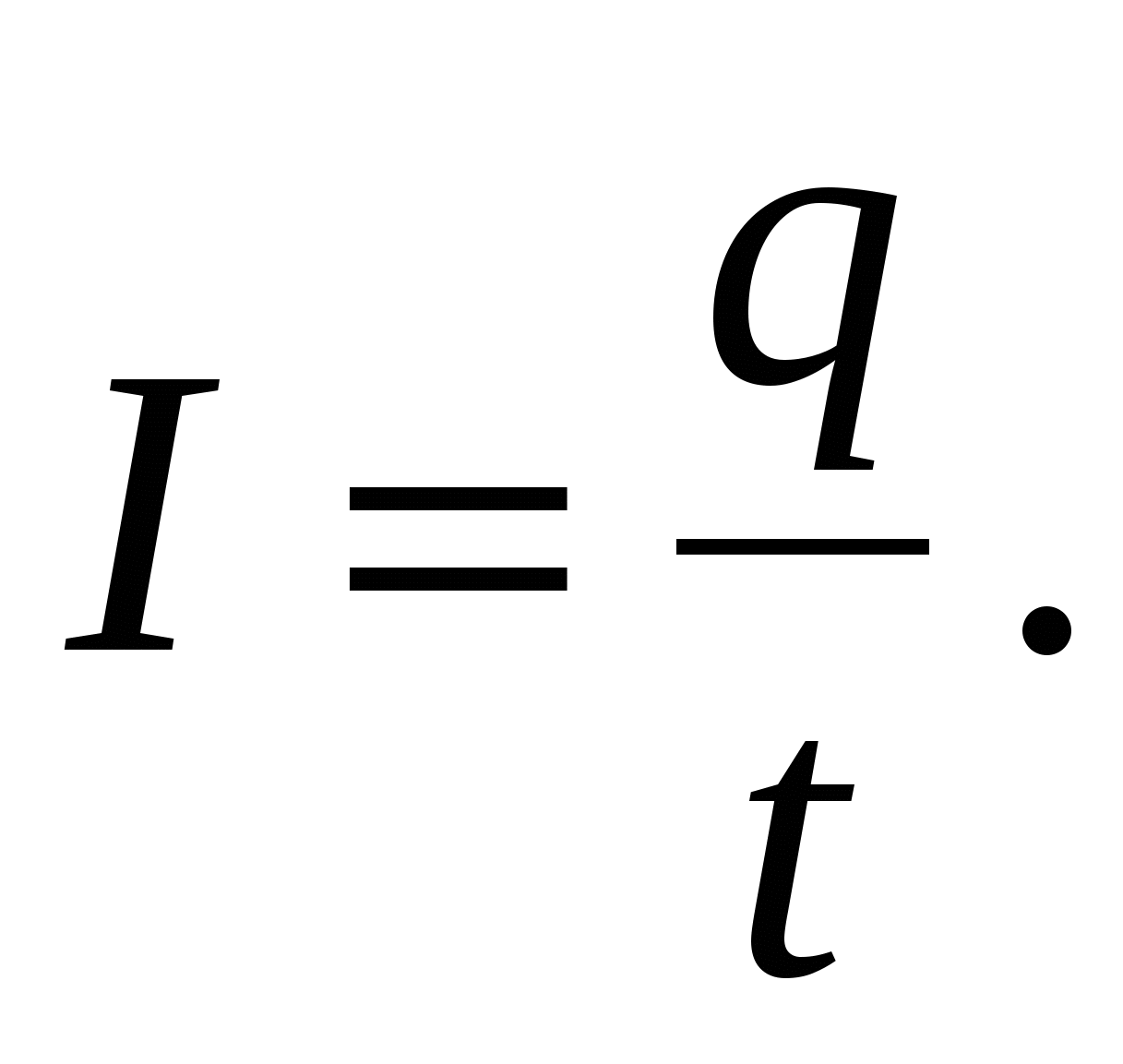
Электрический ток, изменяющийся с течением времени, называется переменным. Примером такого тока является синусоидальный электрический ток, применяемый в электротехнике и электроэнергетике
Единица силы тока – ампер (А) Для характеристики направления электрического тока проводимости в разных точках поверхности проводника и распределения силы тока по этой поверхности вводится плотность тока.
Плотностью тока 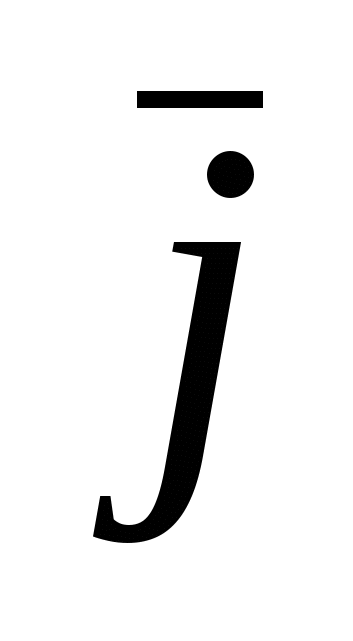 называют векторную физическую величину, совпадающую с направлением тока в рассматриваемой точке и численно равную отношению силы тока dI, проходящего через элементарную поверхность, перпендикулярной направлению тока, к площади этой поверхности:
называют векторную физическую величину, совпадающую с направлением тока в рассматриваемой точке и численно равную отношению силы тока dI, проходящего через элементарную поверхность, перпендикулярной направлению тока, к площади этой поверхности: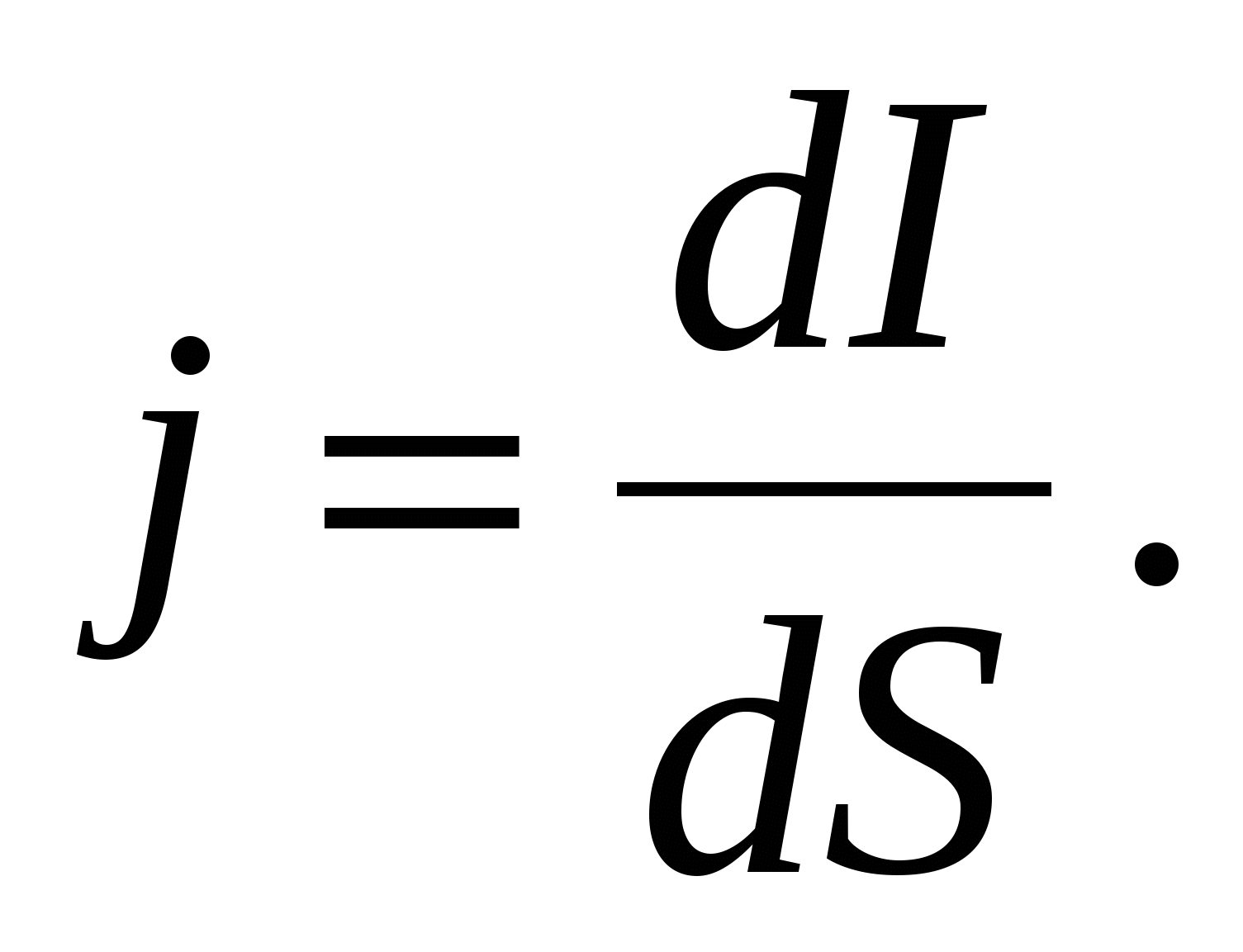 (2.2)
(2.2)
Единица плотности тока – ампер на квадратный метр (А/м2).
Плотность постоянного электрического тока одинакова по всему поперечному сечению однородного проводника. Поэтому для постоянного тока в однородном проводнике с площадью поперечного сечения S сила тока равна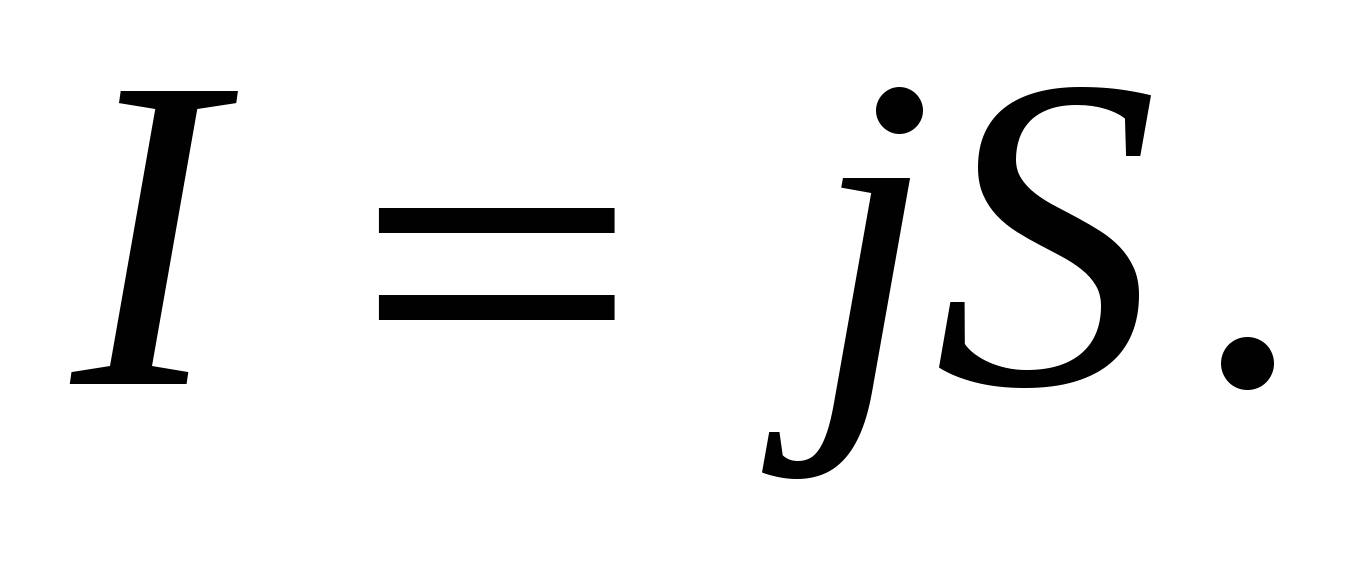
УРАВНЕНИЕ НЕПРЕРЫВНОСТИ При рассмотрении движения зарядов, помимо закона сохранения энергии, необходимо учитывать и закон сохранения электрического заряда. В интегральной форме этот закон можно записать в следующем виде:
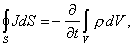
(2) где ρ - плотность заряда. Из этого уравнения следует, что, если объем электронейтрален, то сколько в него втекает зарядов одного знака, столько же и вытекает. С другой стороны , если ток через замкнутую поверхность равен нулю, то заряды внутри
этой поверхности могут рождаться и исчезать только парами (положительных зарядов должно родиться или исчезнуть ровно столько, сколько родилось или исчезло отрицательных. Используя теорему Остроградского-Гаусса, уравнение (2) можно переписать в виде:
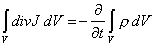
, откуда в дифференциальной форме получим уравнение непрерывности:
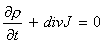
ЗАКОН ОМА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ .ЭЛЕКТРОДВИЖУЩАЯ СИЛА. Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение зарядов от точек с большим потенциалом к точкам с меньшим потенциалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению тока. Поэтому для поддержания постоянного электрического тока в цепи необходимо наличие устройства, способного создавать и поддерживать разность потенциалов за счет работы некоторых сторонних сил. Такие устройства называют
источниками тока.
Под действием сторонних сил носители тока движутся внутри источника электрической энергии против сил электростатического поля (против кулоновских сил, вызывающих соединение разноименных зарядов, а следовательно, выравнивание потенциалов и исчезновение тока), так что на концах внешней цепи поддерживается постоянная разность потенциалов и в цепи протекает постоянный электрический ток.
Сторонние силы совершают работу по перемещению электрических зарядов.
Физическая величина, определяемая работой сторонних сил при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС)источника: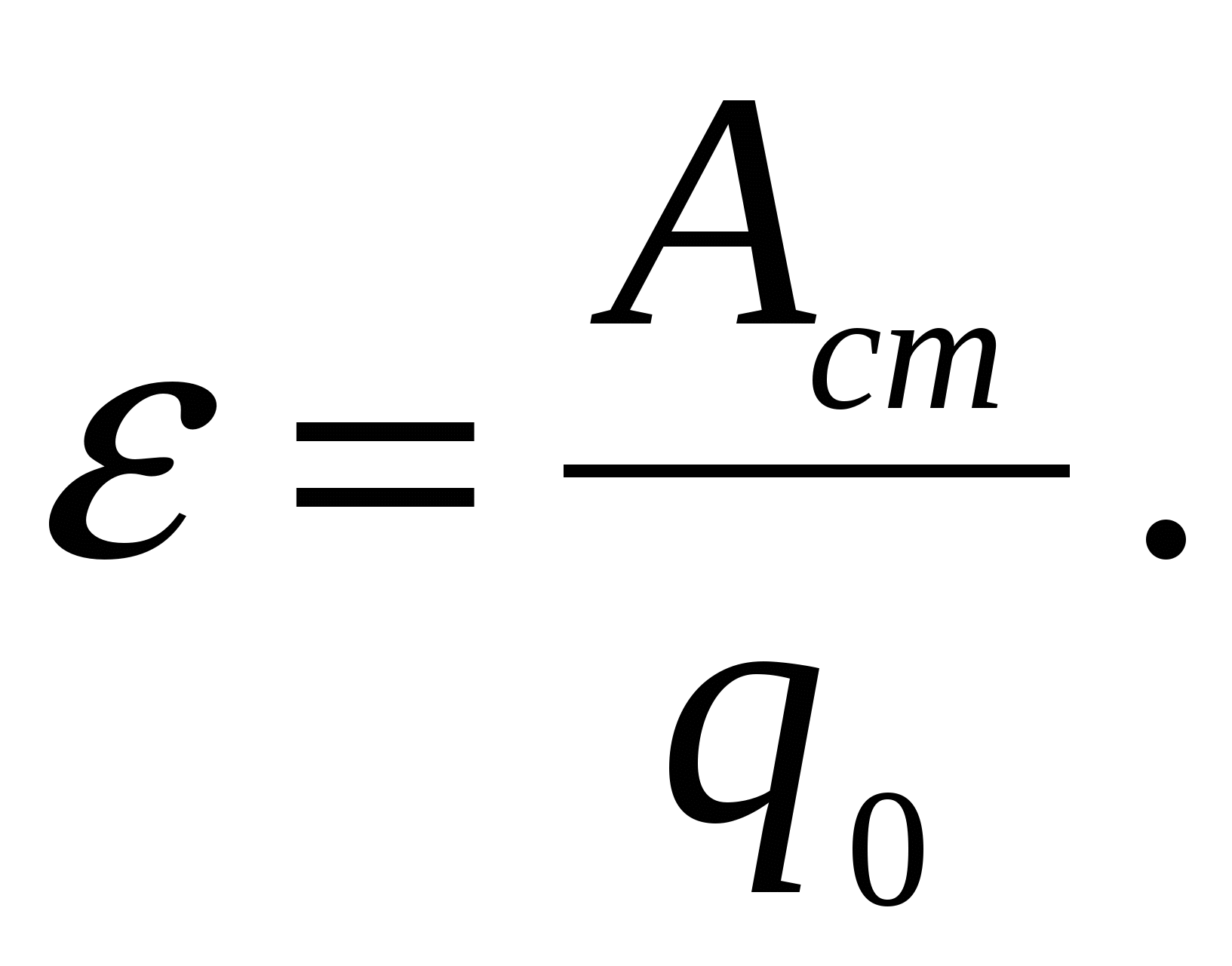
(2.3)Единица ЭДС –
вольт (В).Сторонняя сила, действующая на заряд
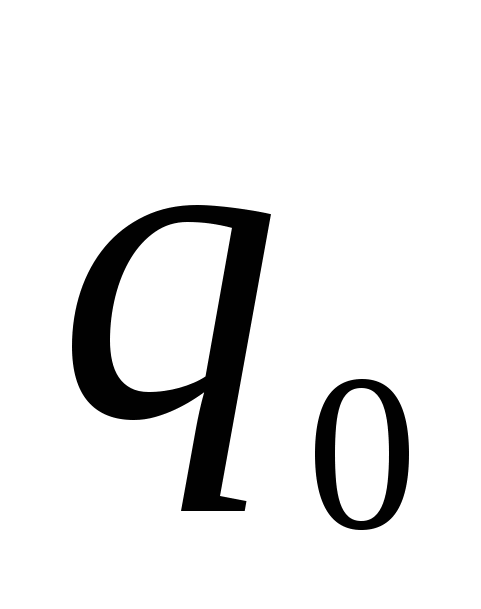
, может быть выражена через напряженность
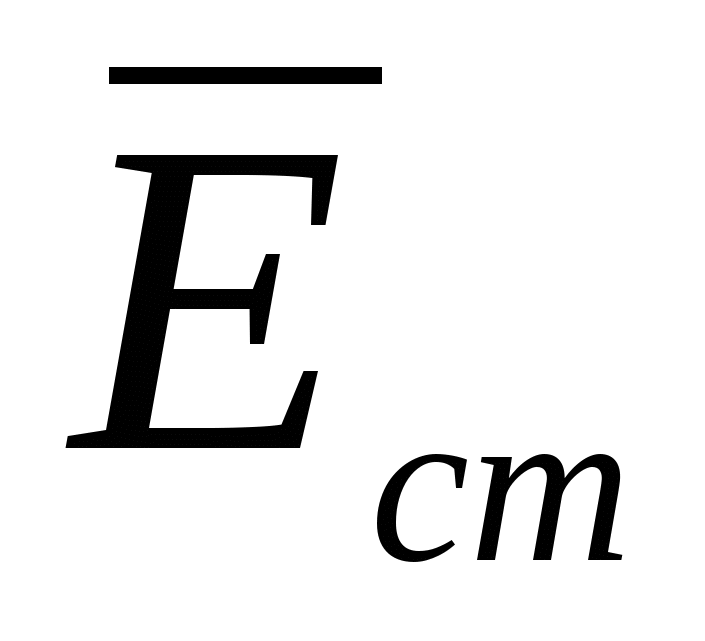 поля сторонних сил
поля сторонних сил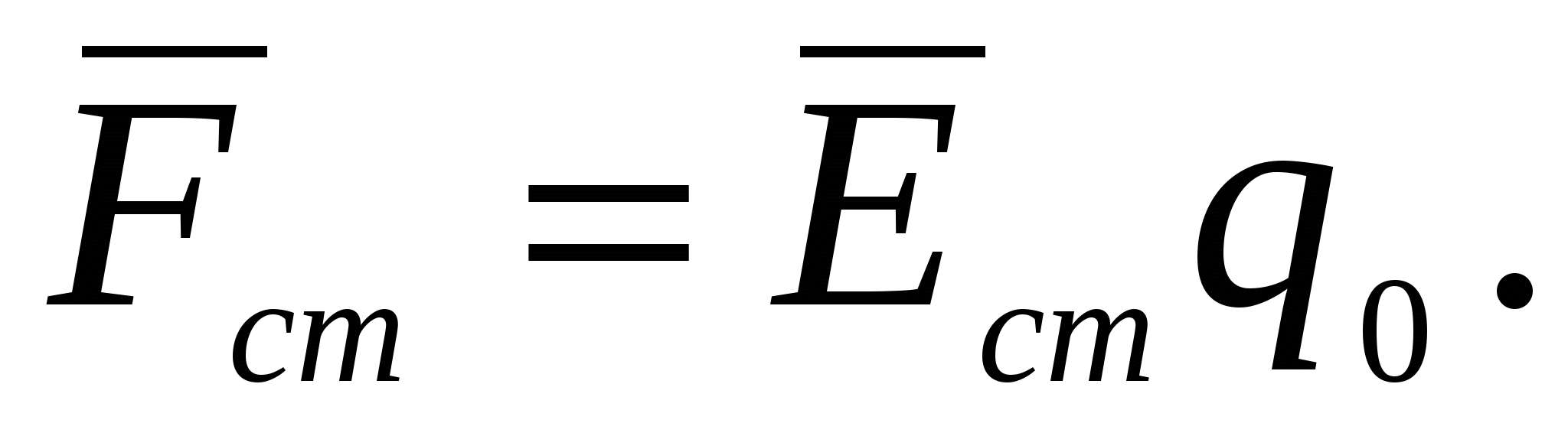
Тогда работа сторонних сил по перемещению заряда
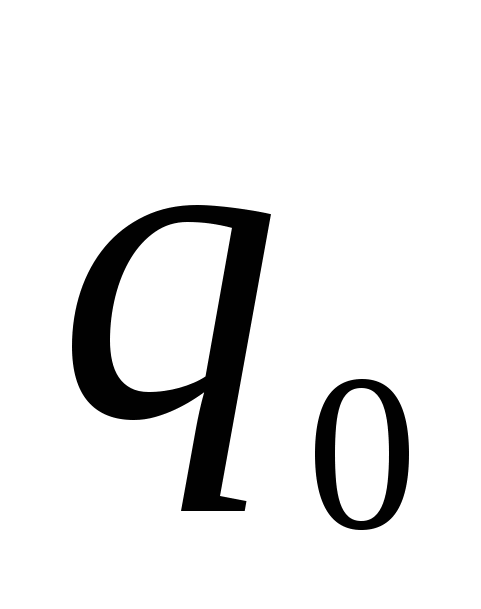
на замкнутом участке цепи будет равна:
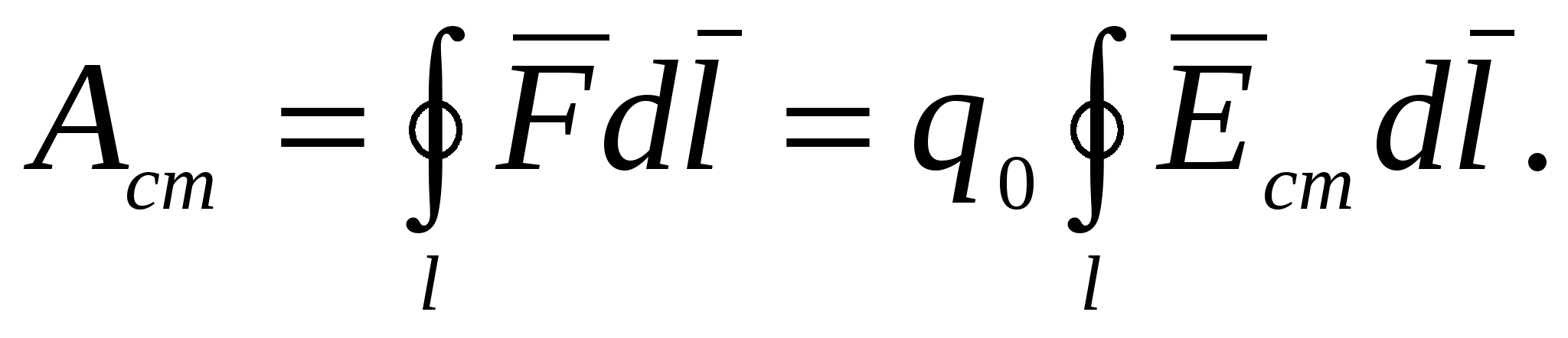
(2.4)Разделив (2.4) на
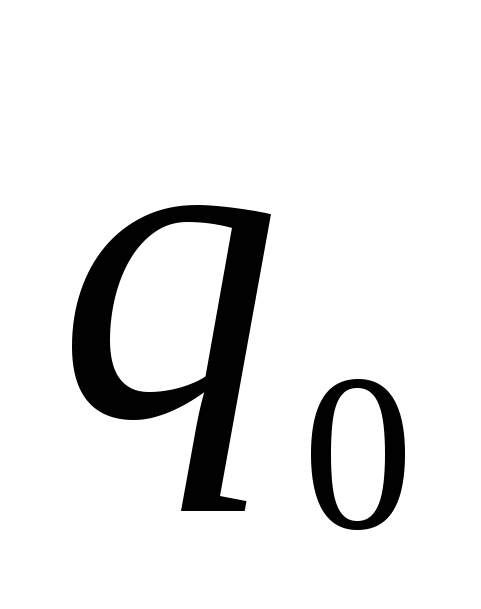
и учитывая (2.3), получим выражение для ЭДС, действующей в цепи:
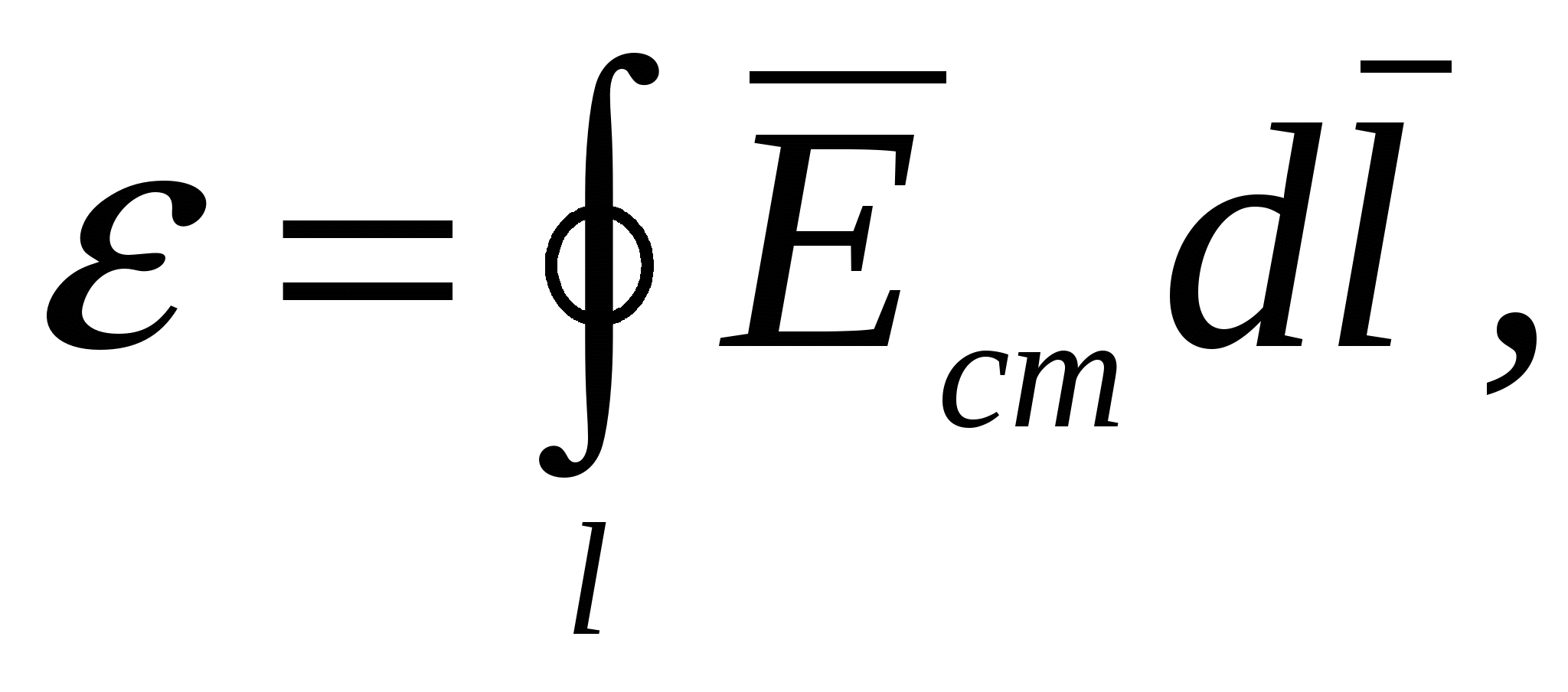
т.е. ЭДС, действующая в замкнутой цепи, есть циркуляция вектора напряженности поля сторонних сил. Как частный случай, ЭДС на участке 1-2 цепи будет равна:
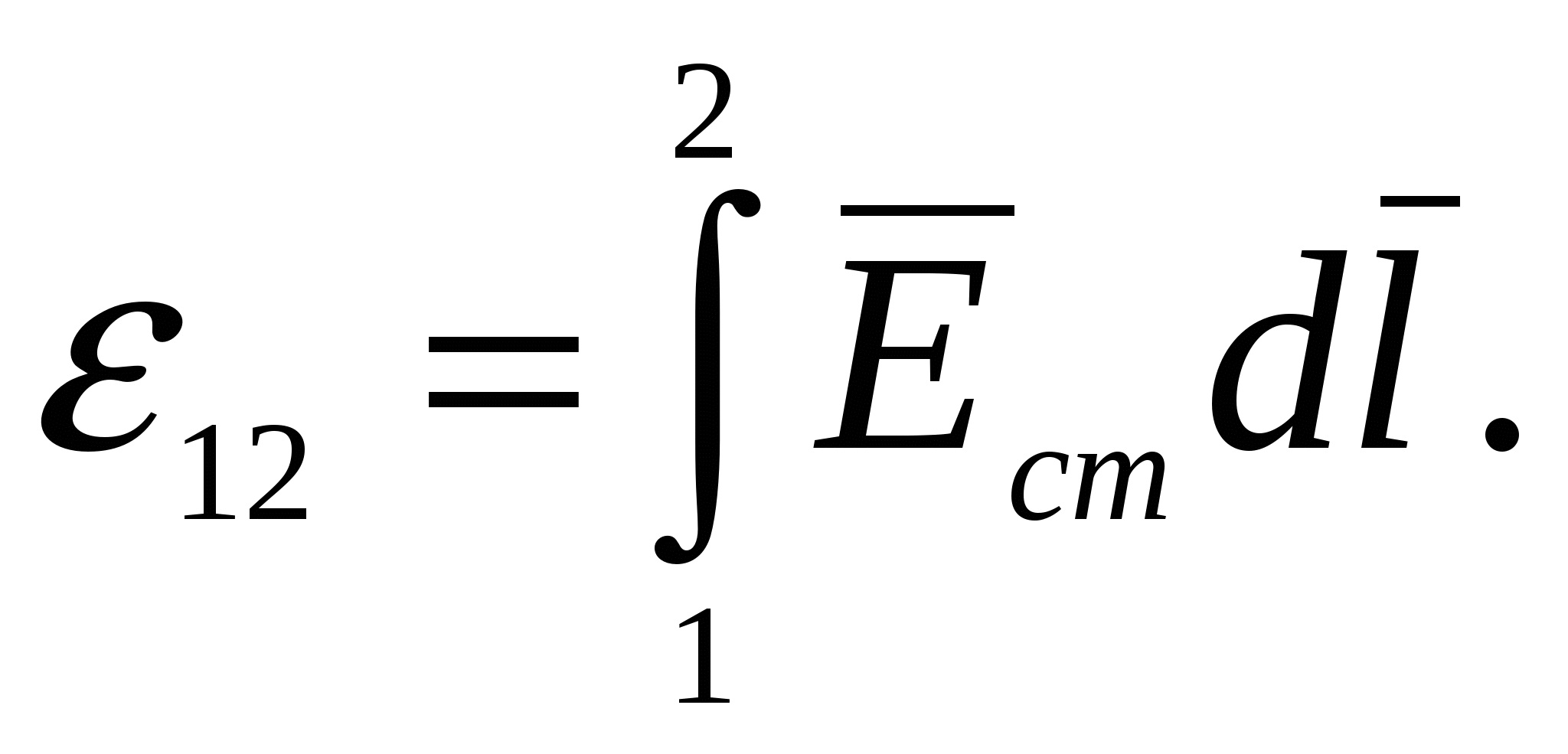
(2.5)На заряд
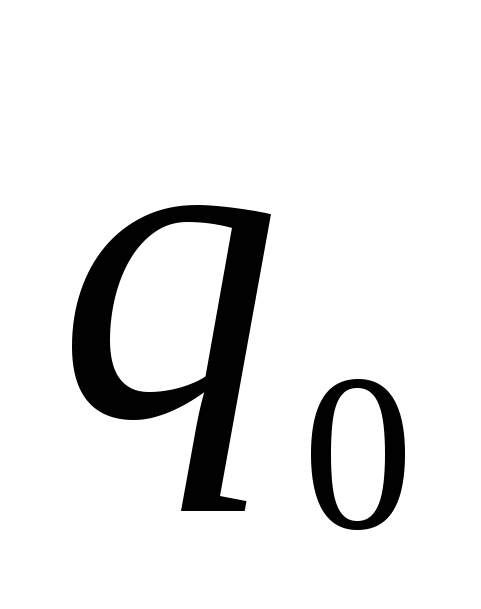
помимо сторонних сил действуют также силы электростатического поля (кулоновские силы)
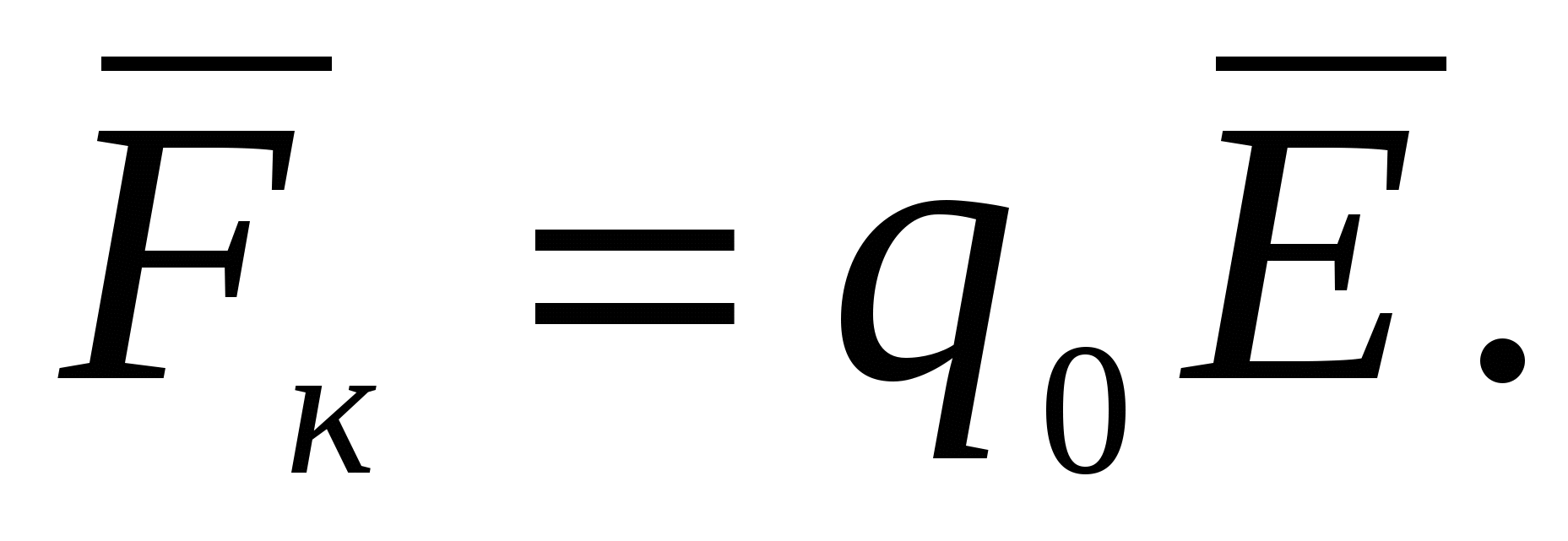
Результирующая сила, действующая в цепи на заряд
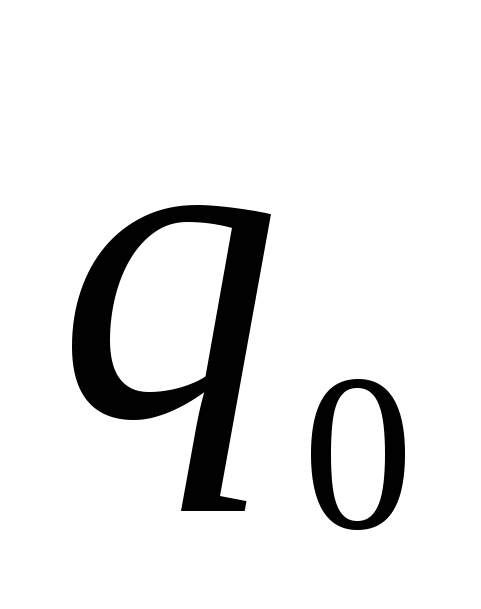
, определяется следующим образом:
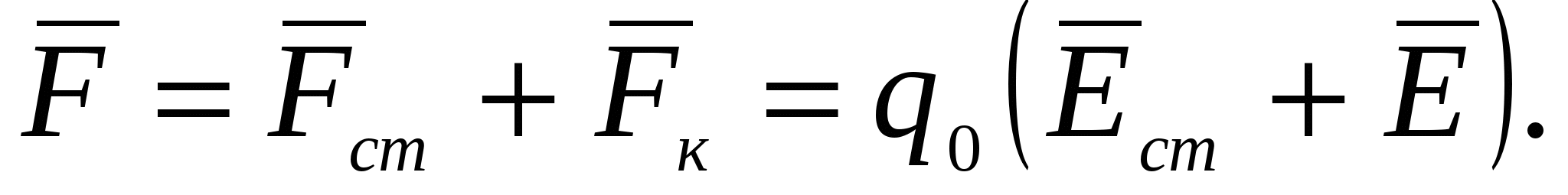
Тогда работа, совершаемая этой силой над зарядом
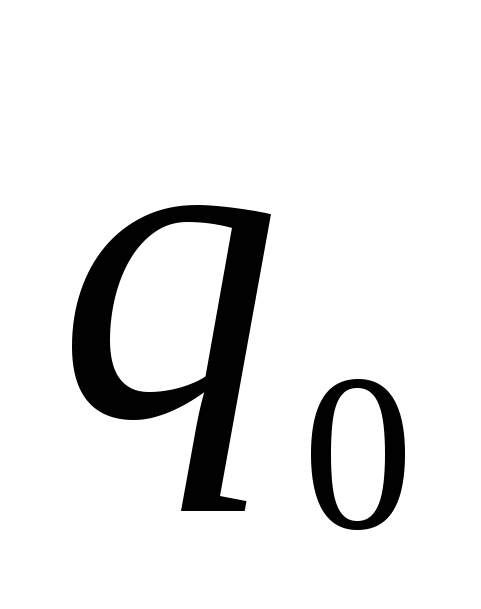
на участке 1-2 цепи, равна
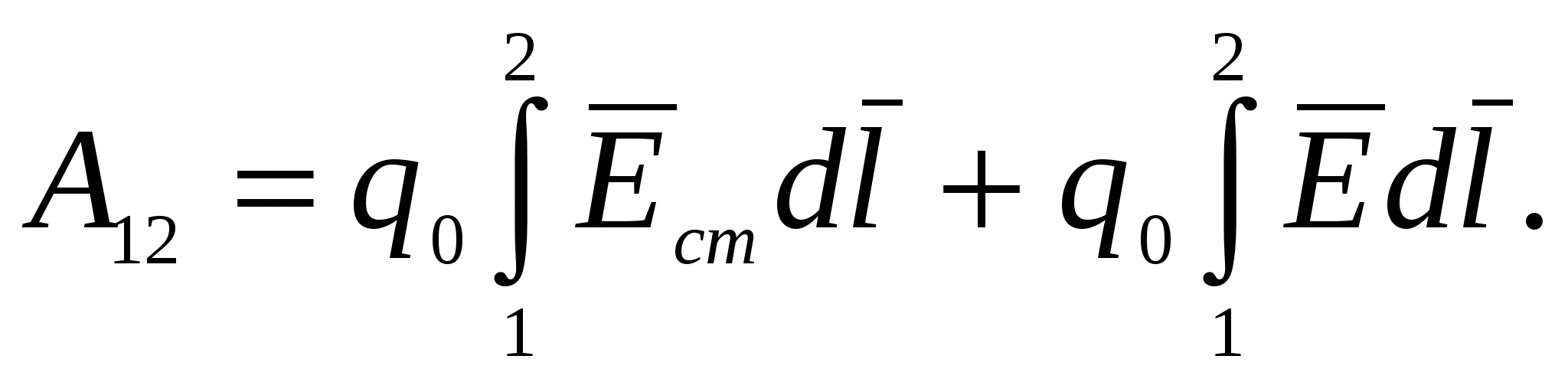
Используя выражение (2.5) и ранее полученное соотношение
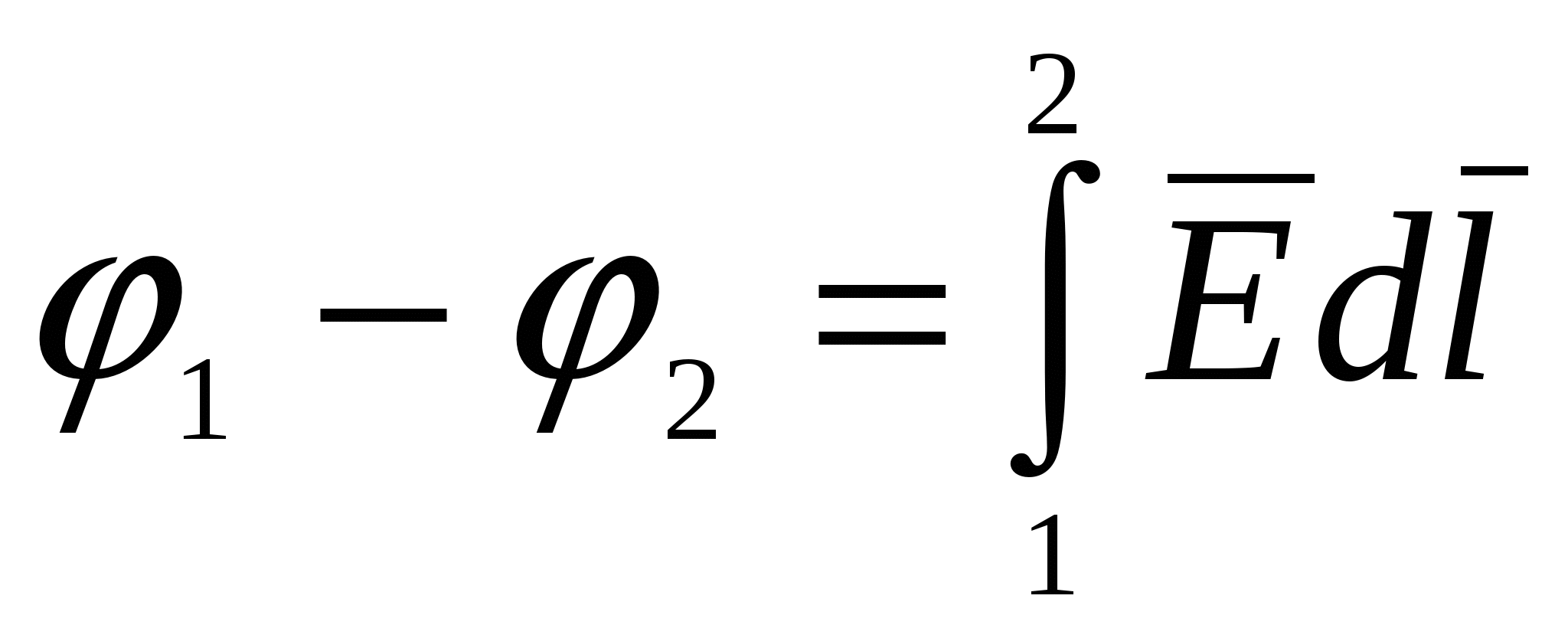
, можем записать:
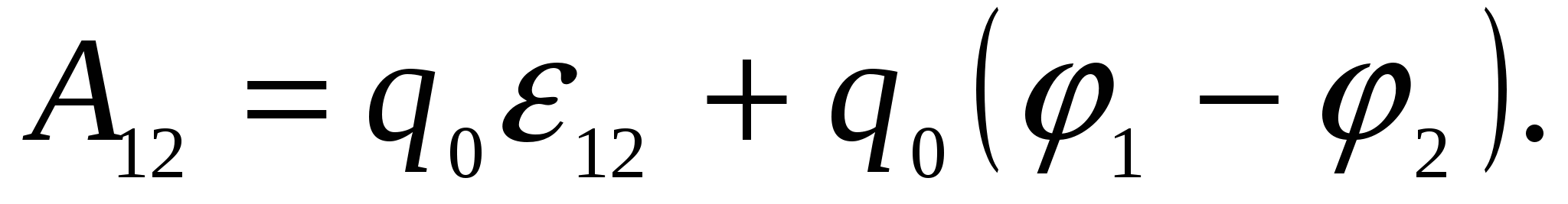
(2.6)Для замкнутой цепи работа электростатических сил равна нулю, поэтому в такой цепи
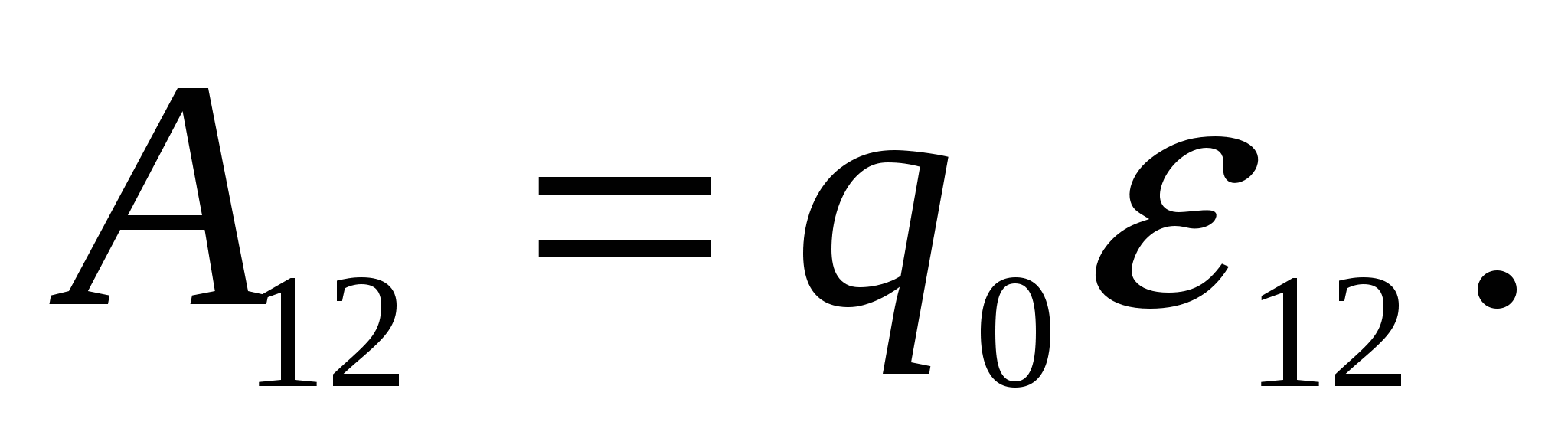
Разделив (2.6) на
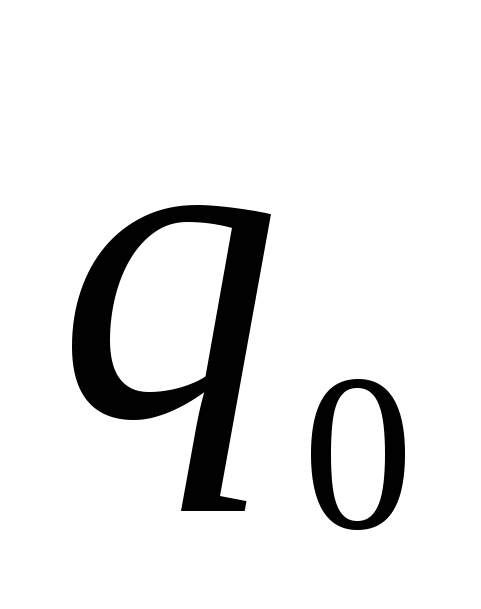
, получим
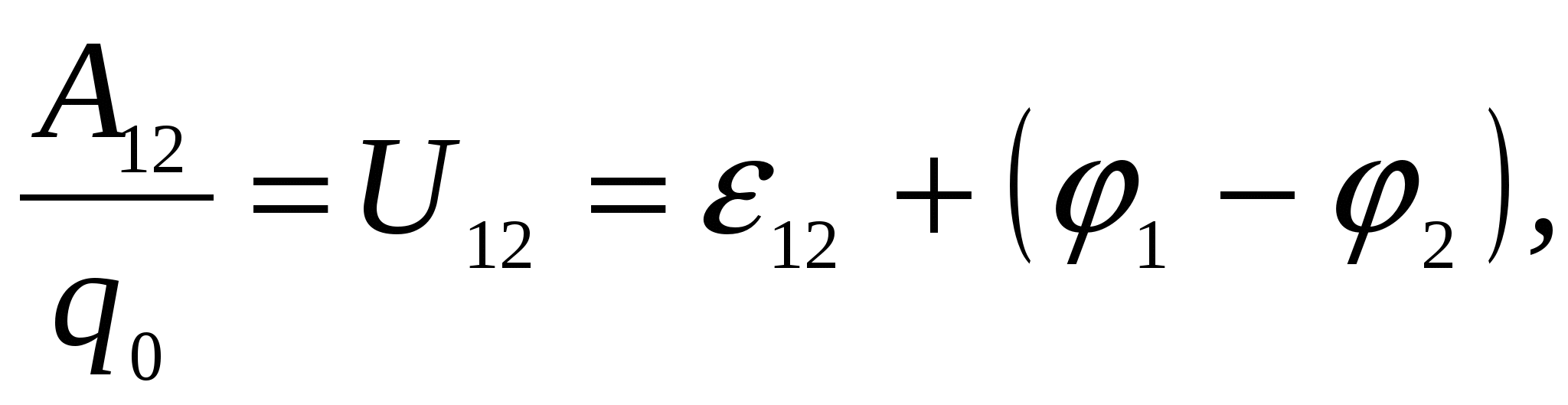
(2.7)т.е
. напряжением на участке цепи называется физическая величина, определяемая работой, совершаемой суммарным полем кулоновских и сторонних сил при перемещении единичного положительного заряда.
Таким образом, напряжение является более общим понятием, чем разность потенциалов: напряжение на участке цепи равно разности потенциалов только в том случае, если на этом участке не действует ЭДС, т.е. сторонними силами не совершается работа. Такой участок электрической цепи называется
однородным.
Ом экспериментально установил, что сила тока в однородном проводнике пропорциональна разности потенциалов на его концах и обратно пропорциональна сопротивлению проводника (
закон Ома для участка цепи): (2.8)Электрическое сопротивление металлического проводника обусловлено тем, что свободные электроны при своем движении взаимодействуют (соударяются) с положительными ионами кристаллической решетки. Поэтому сопротивление проводников зависит прежде всего от материала проводника.Для однородного цилиндрического проводника длиной
l и площадью поперечного сечения
S сопротивление определяется по формуле
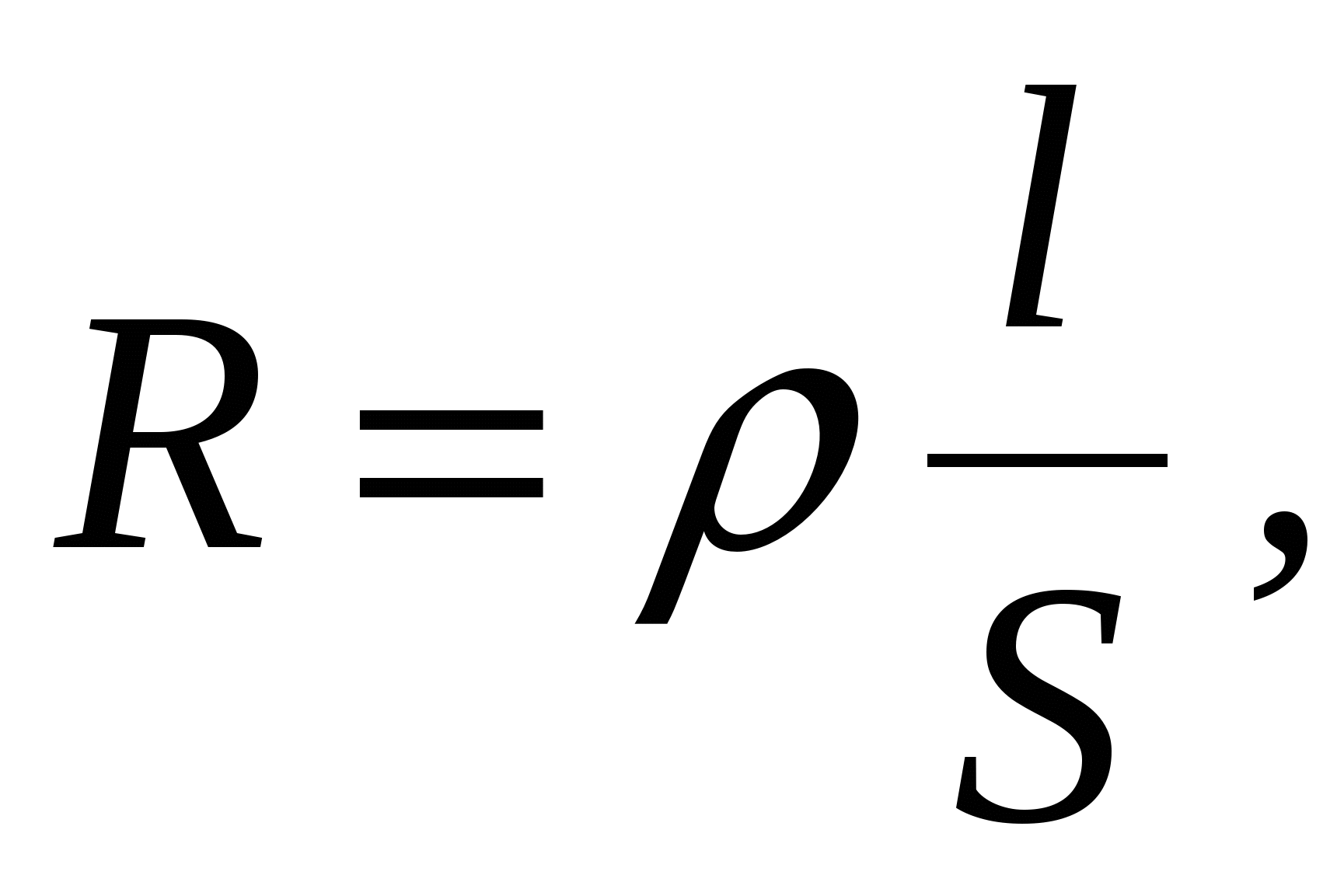
(2.9)где
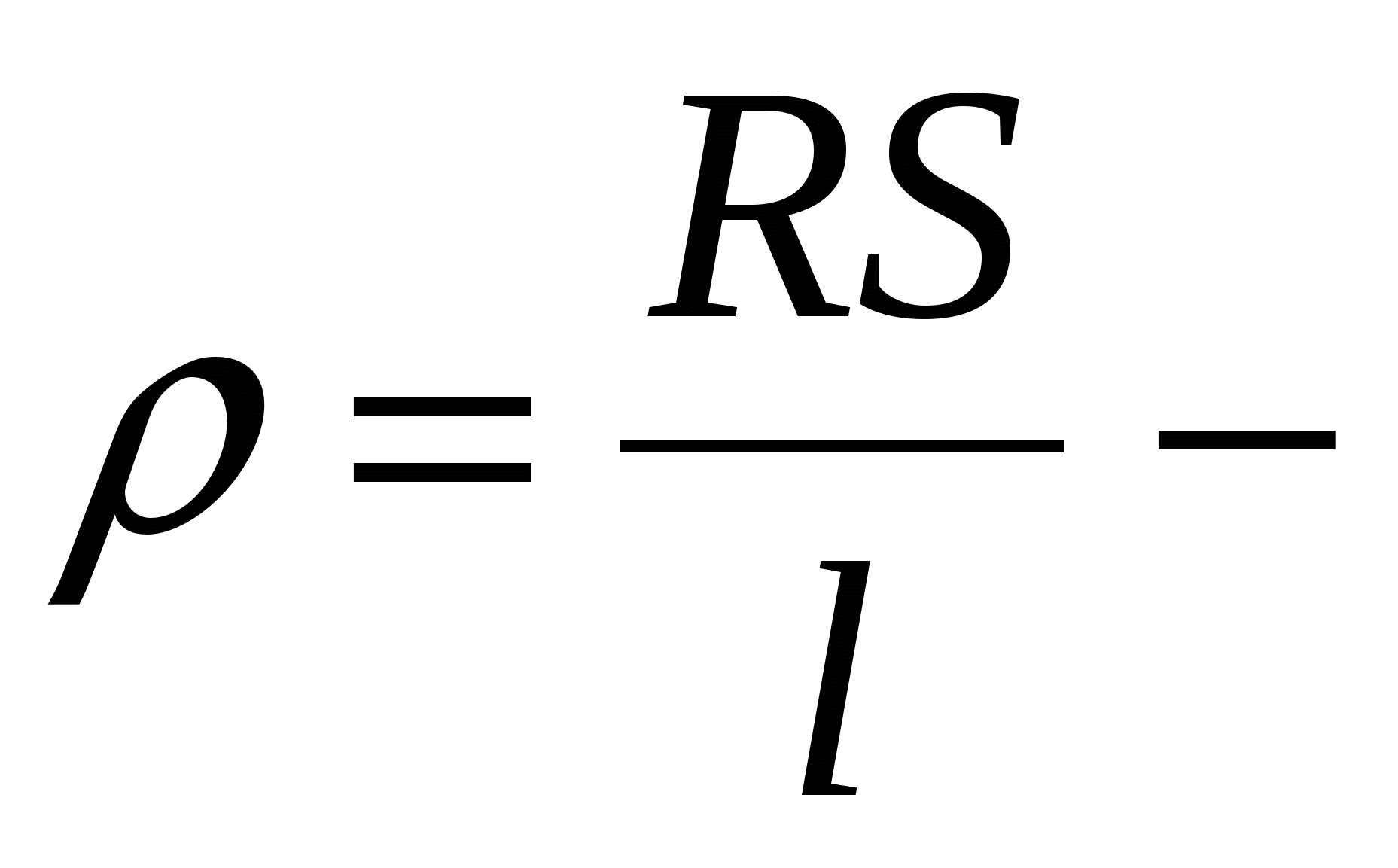 удельное сопротивление
удельное сопротивление (сопротивление однородного цилиндрического проводника, имеющего единичную длину и единичную площадь поперечного сечения), характеризующее материал проводника.Ед. сопротивления –
ом:
1 Ом – сопротивление такого проводника, в котором при напряжении
1 В течет постоянный ток силой
1 А.Величина
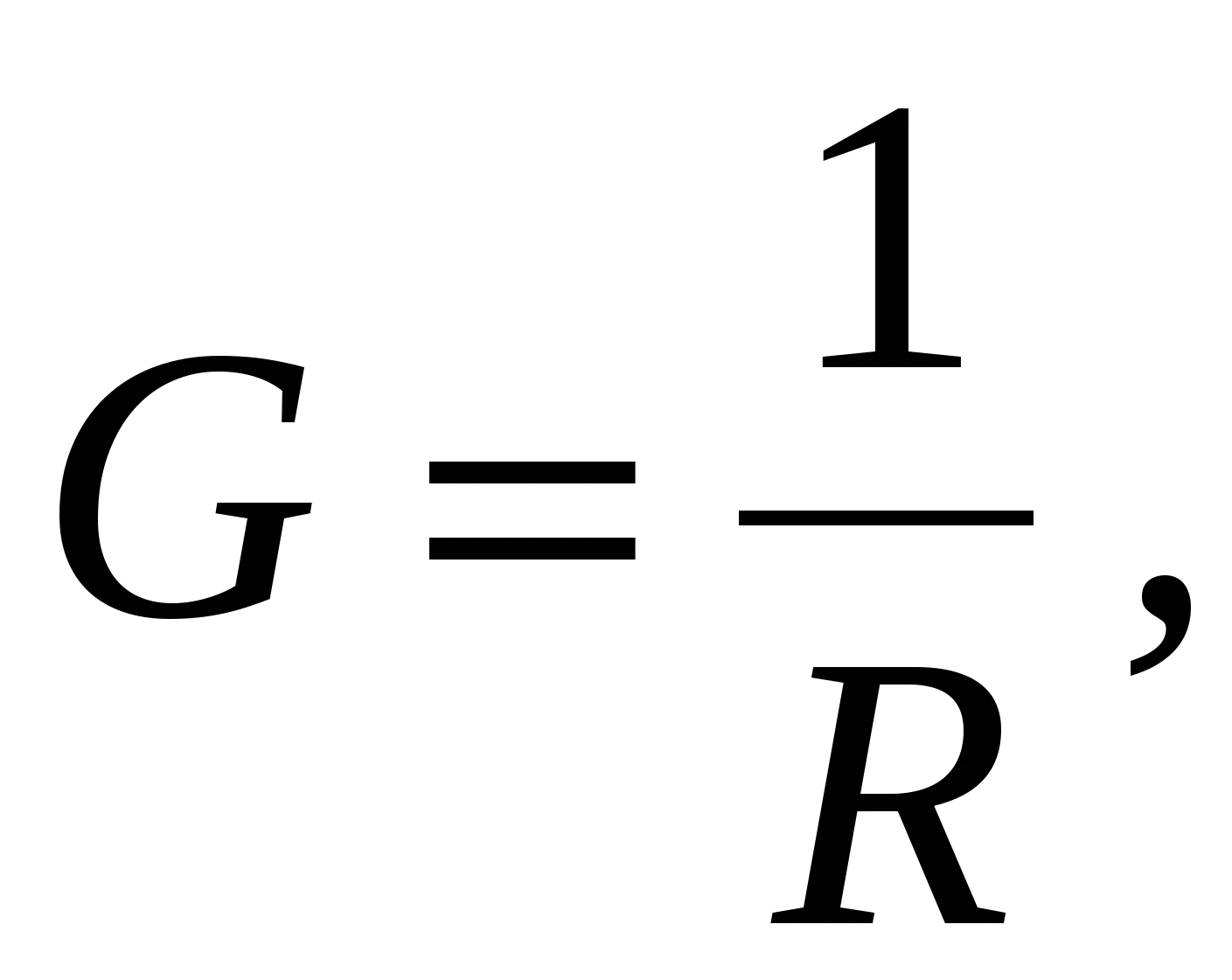
обратная сопротивлению, называется
электрической проводимостью. Единица проводимости –
сименс:
1 См – электрическая проводимость проводника сопротивлением
1 Ом.
Удельное электрическое сопротивление проводника зависит не только от рода вещества, но и от температуры:
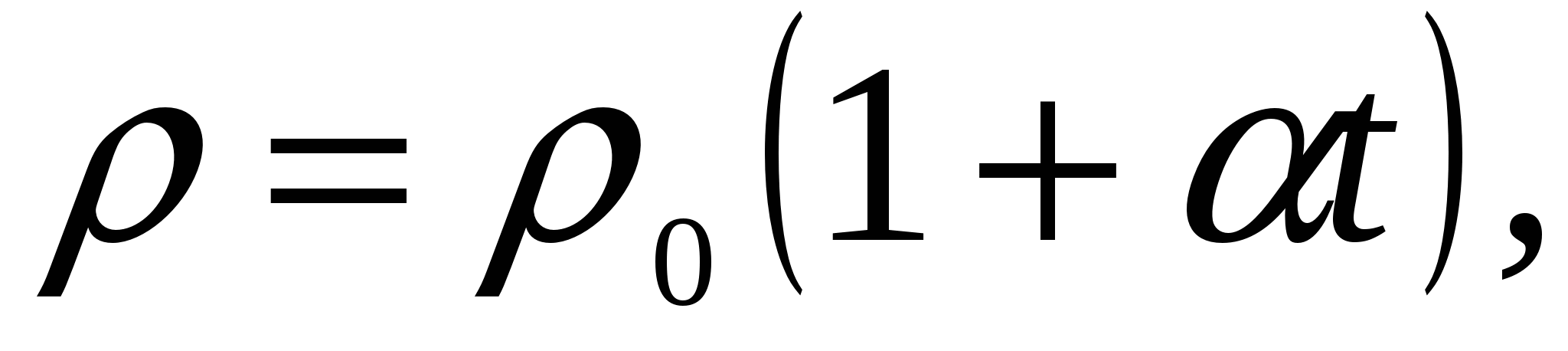
(2.10)где
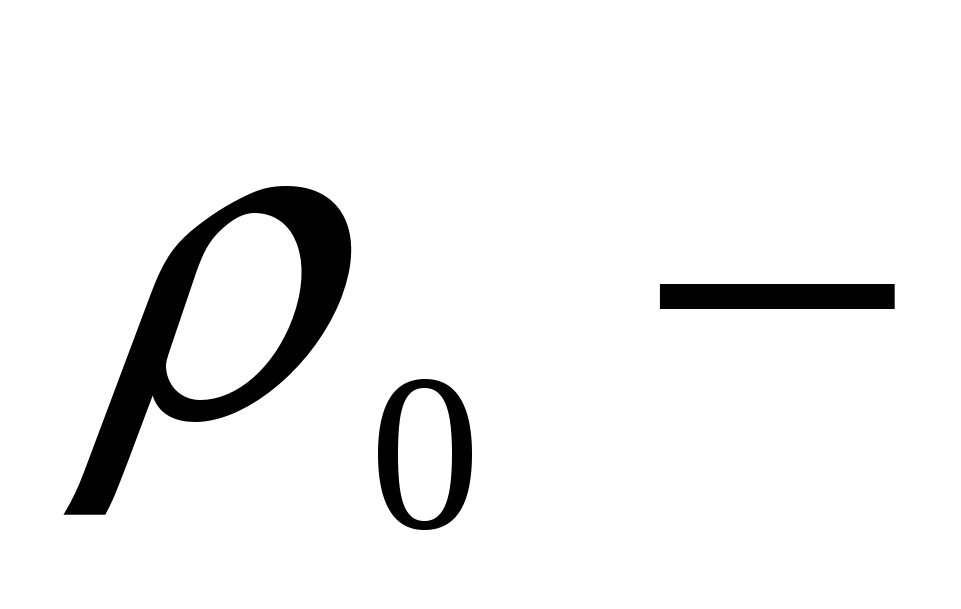
удельное сопротивление при
0оС;
t – температура (по шкале Цельсия);
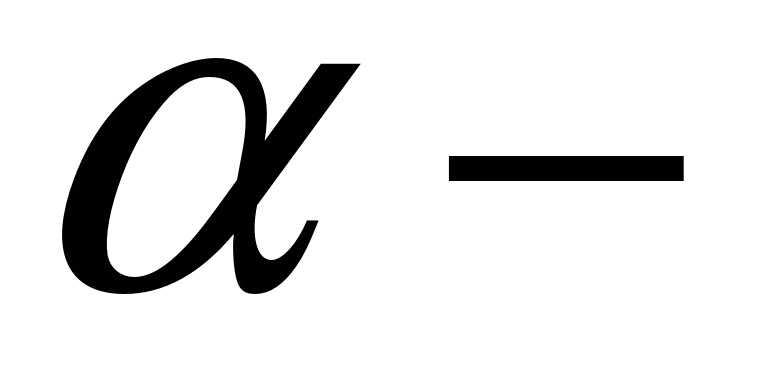
температурный коэффициент сопротивления, характеризующий относительное изменение сопротивления проводника при его нагревании на
1 оС или
1 К. Температурные коэффициенты сопротивления веществ различны при разных температурах. Однако для многих металлов изменение

с температурой невелико. Для всех чистых металлов
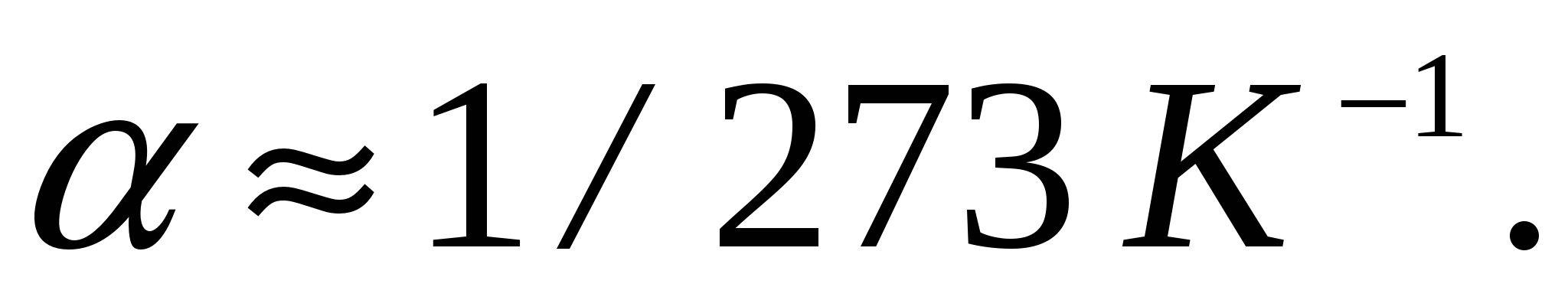
Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (2.9) в закон Ома
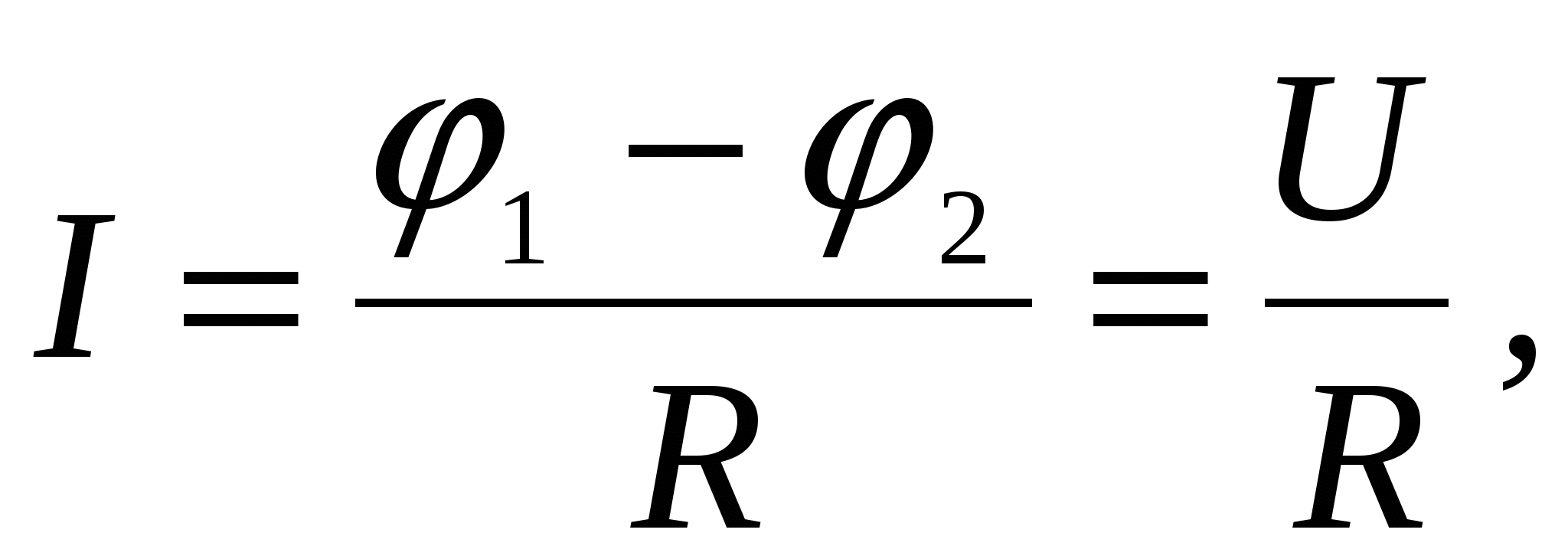
, получим:
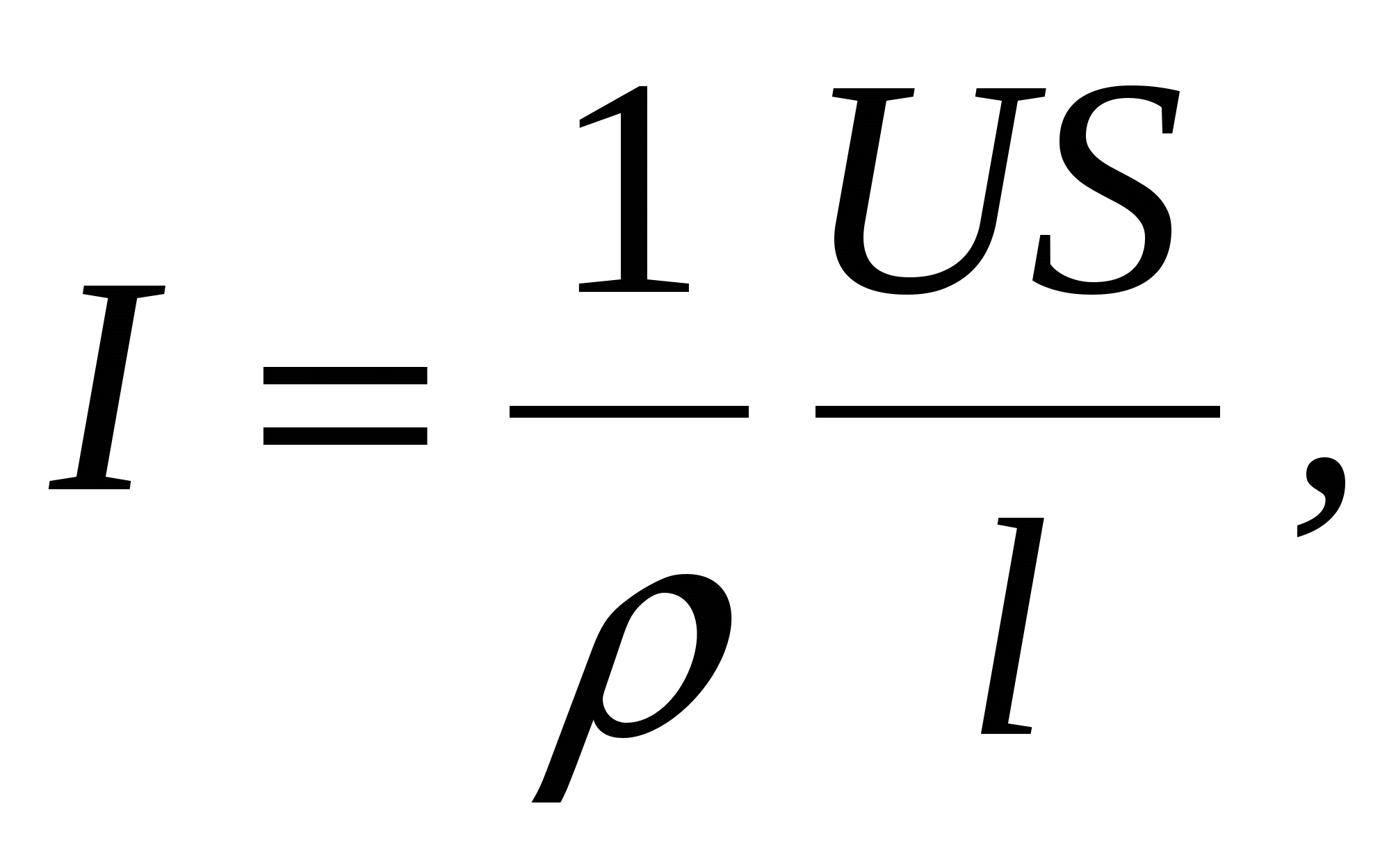
или
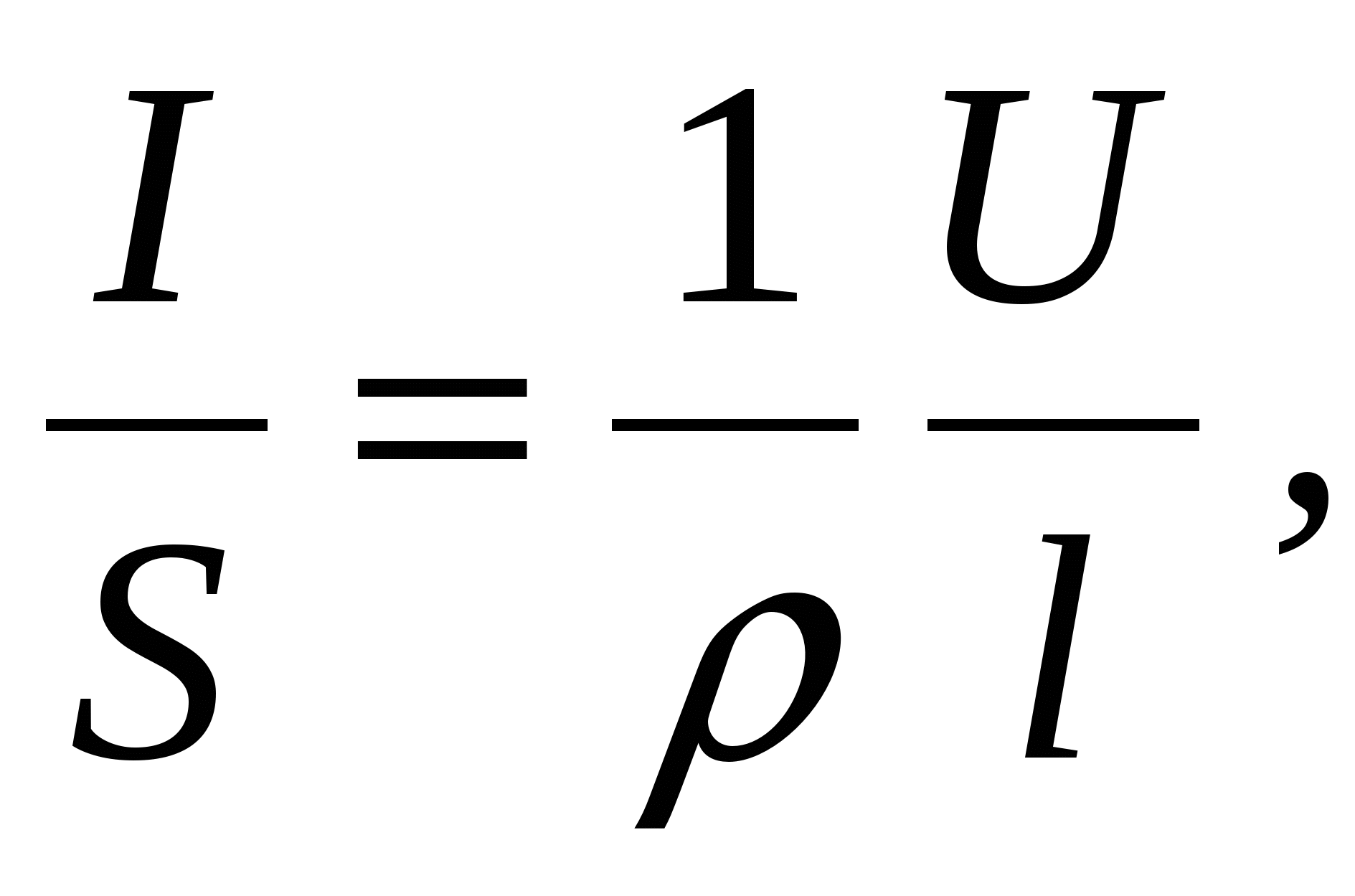
где величина 1/ρ=δ называется
удельной проводимостью (
См/м). Учитывая, что
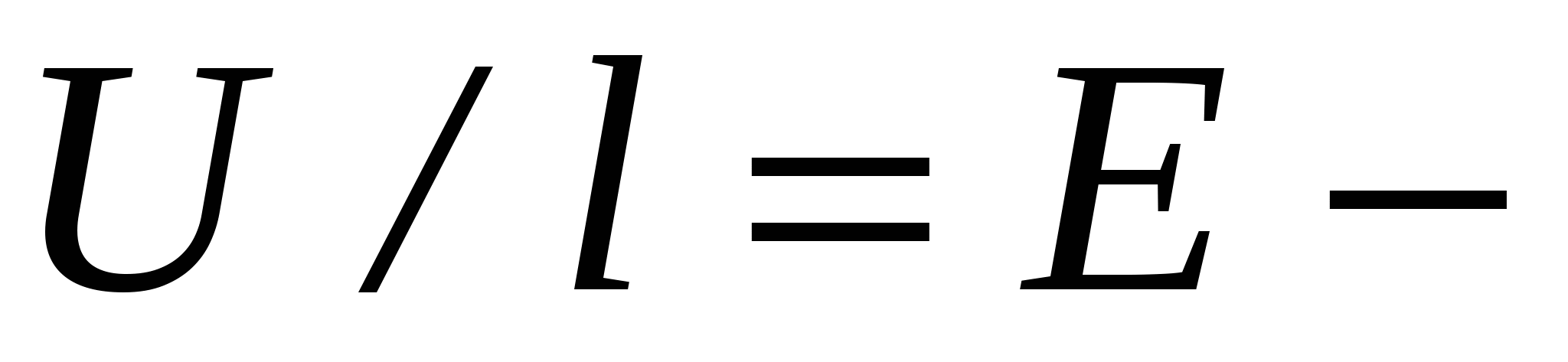
напряженность электрического поля в проводнике, а
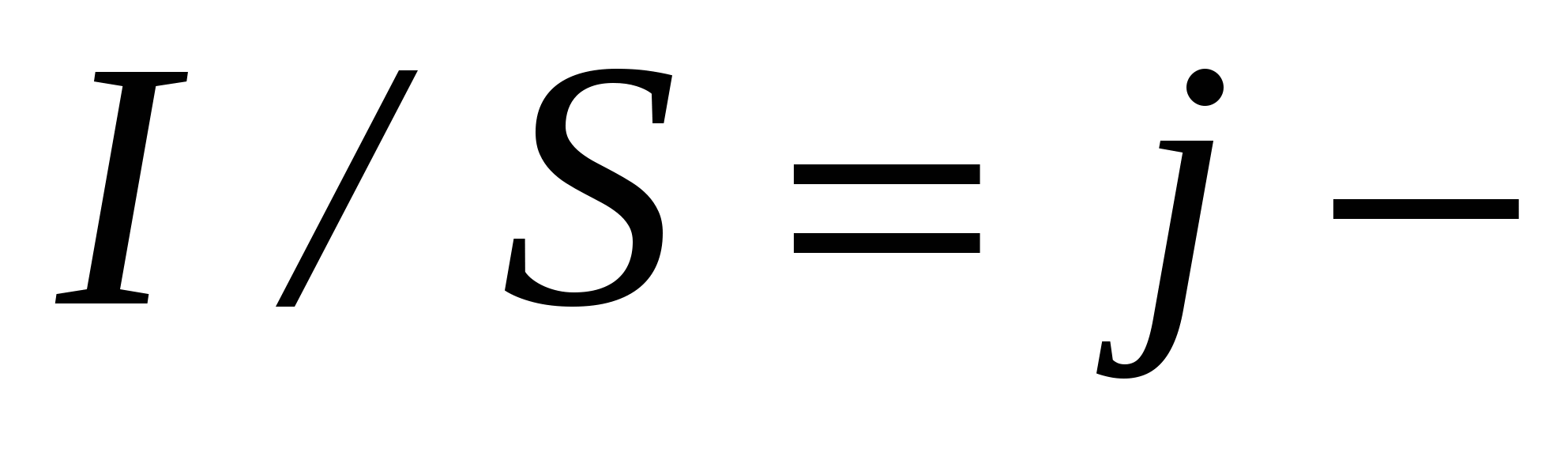
плотность тока, последнее выражение можно записать в следующем виде: j=δE
Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора
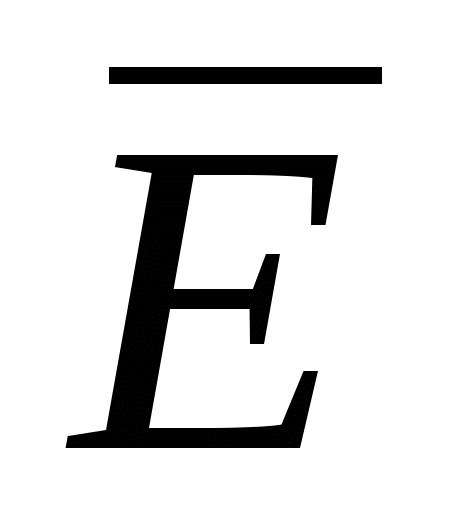
, то направления
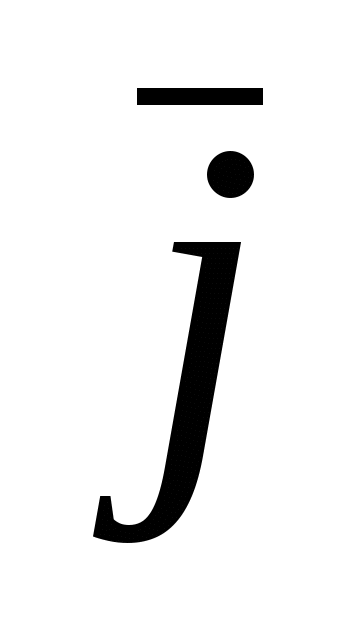
и δ совпадают. Поэтому в окончательном виде
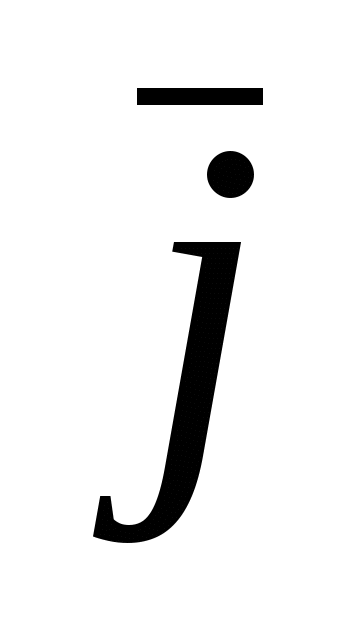
=δ
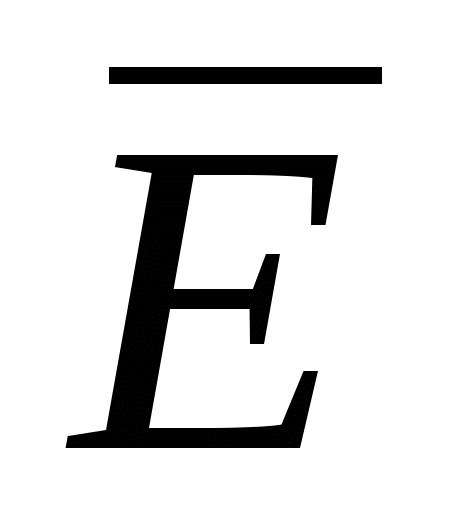
(2.11)Выражение (2.11) представляет собой
закон Ома в дифференциальной форме, который связывает плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.
РАБОТА И МОЩНОСТЬ ТОКА.ЗАКОН ДЖОУЛЯ-ЛЕНЦАРассмотрим однородный проводник, по концам которого приложено напряжение
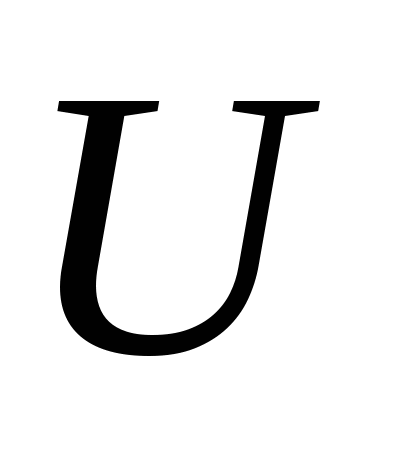
. За время
dt через поперечное сечение проводника переносится заряд
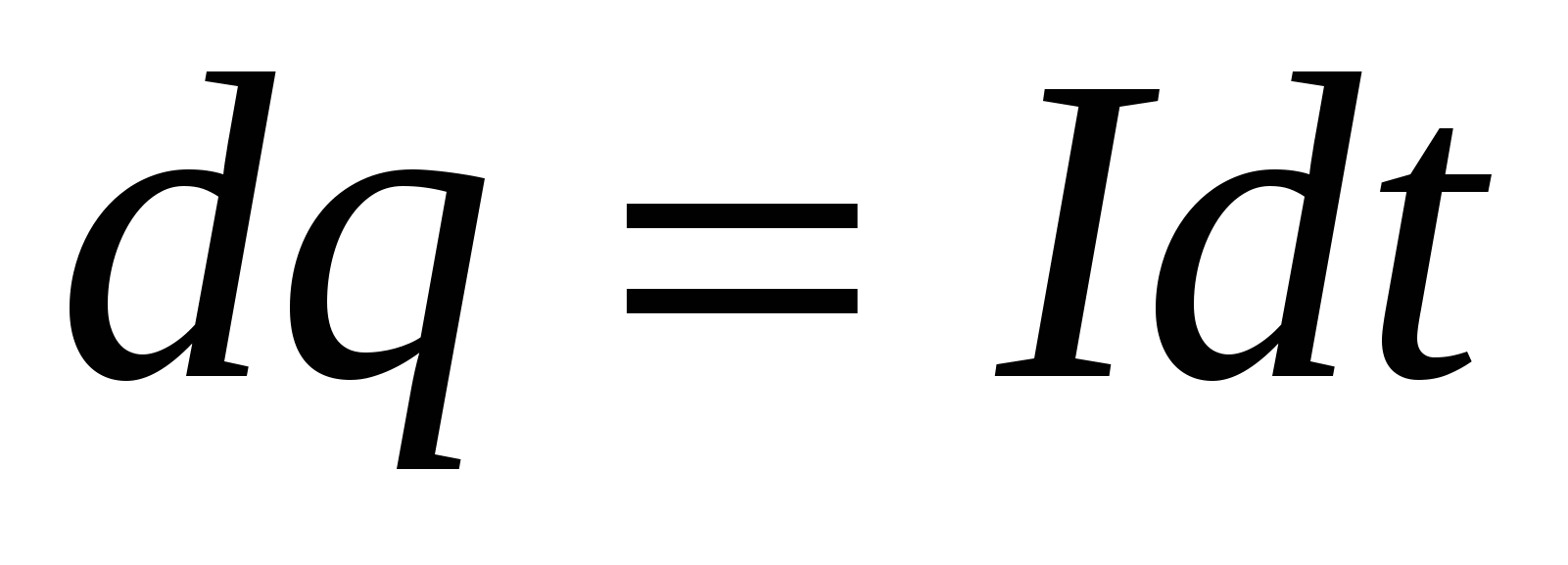
. Так как ток представляет собой перемещение заряда
dq под действием электрического поля, работа тока есть
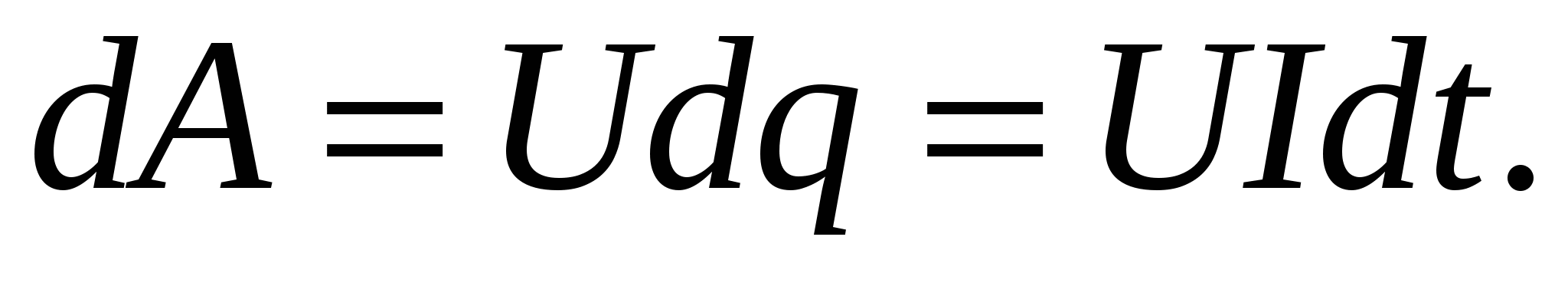
(2.14)Используя закон Ома для однородного участка цепи, формулу (2.14) можно представить в виде
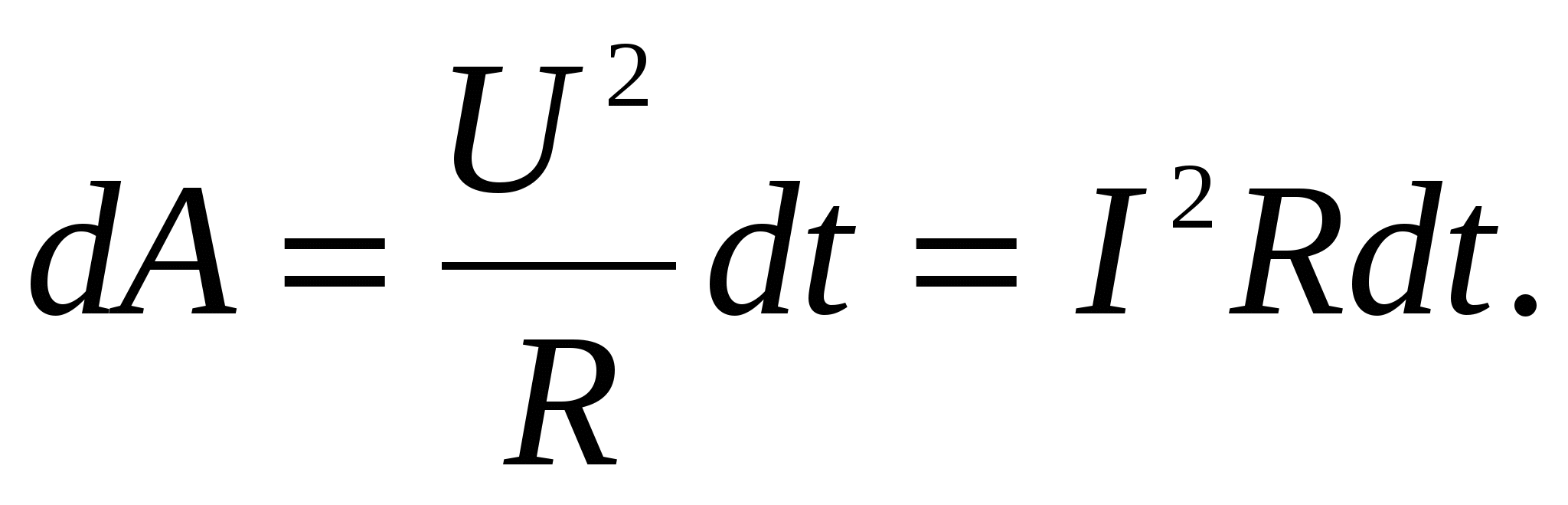
(2.15)
Мощность электрического тока – это быстрота совершения работы, т.е.
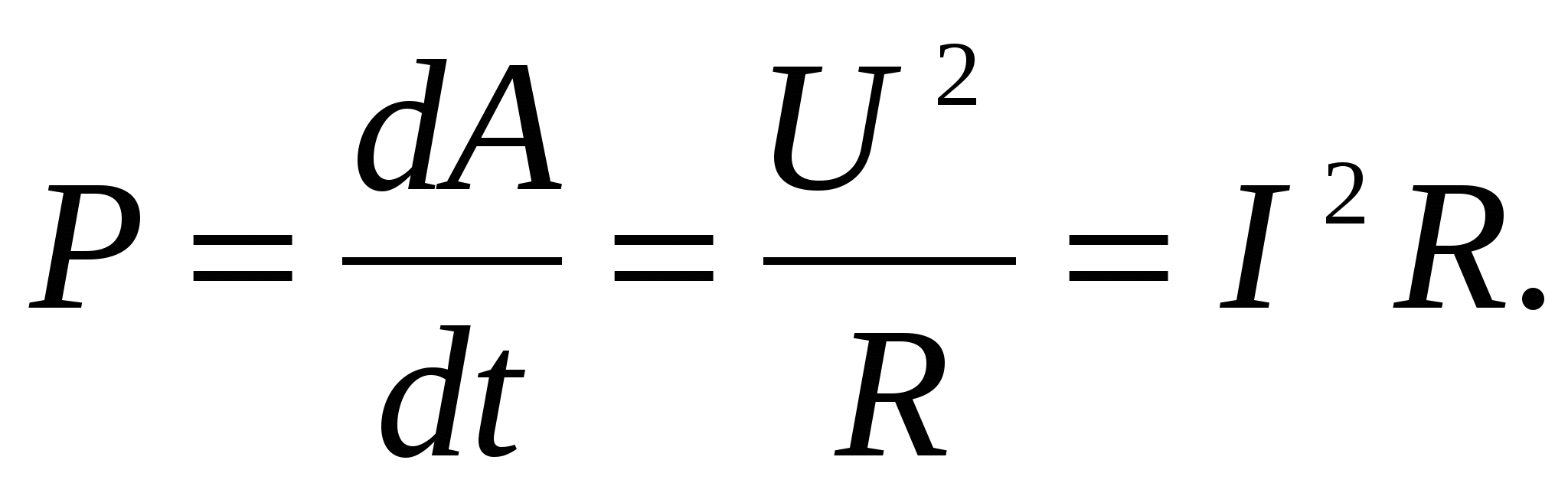
(2.16)Единица мощности –
ватт:
1 Вт – мощность, выделяемая в проводнике за
1 с при протекании тока силой
1 А.Если ток протекает по неподвижному металлическому проводнику, то вся работа тока затрачивается на его нагревание и по закону сохранения энергии
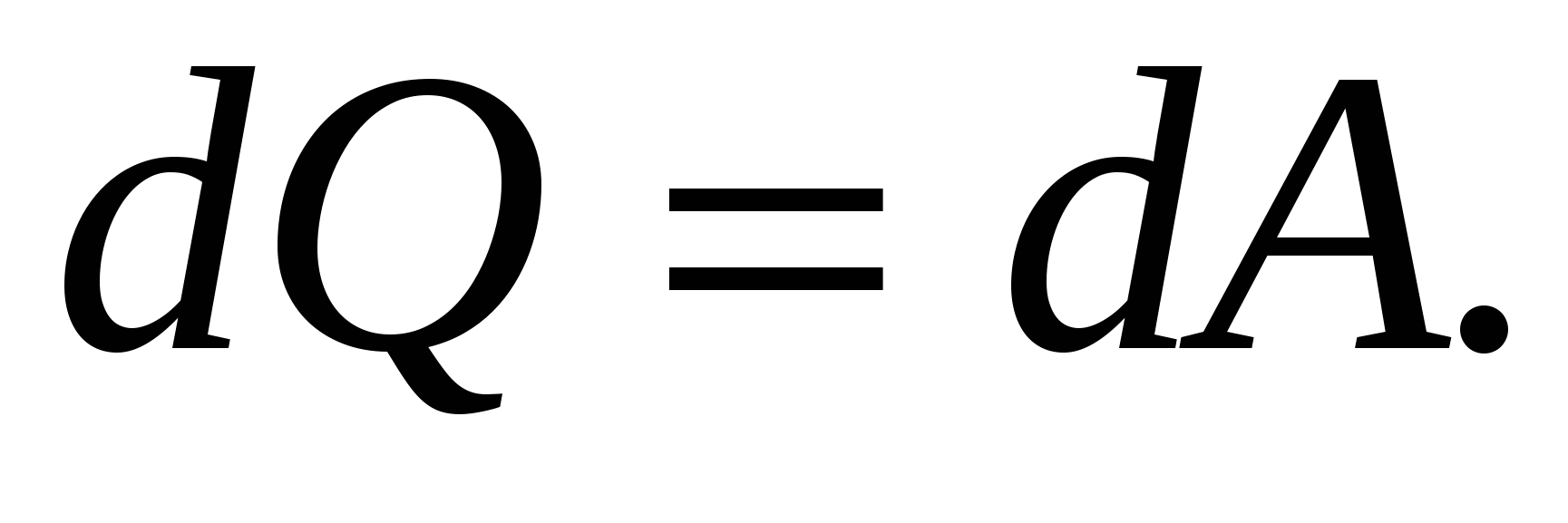
Таким образом, с учетом (2.14) и (2.15) получим:
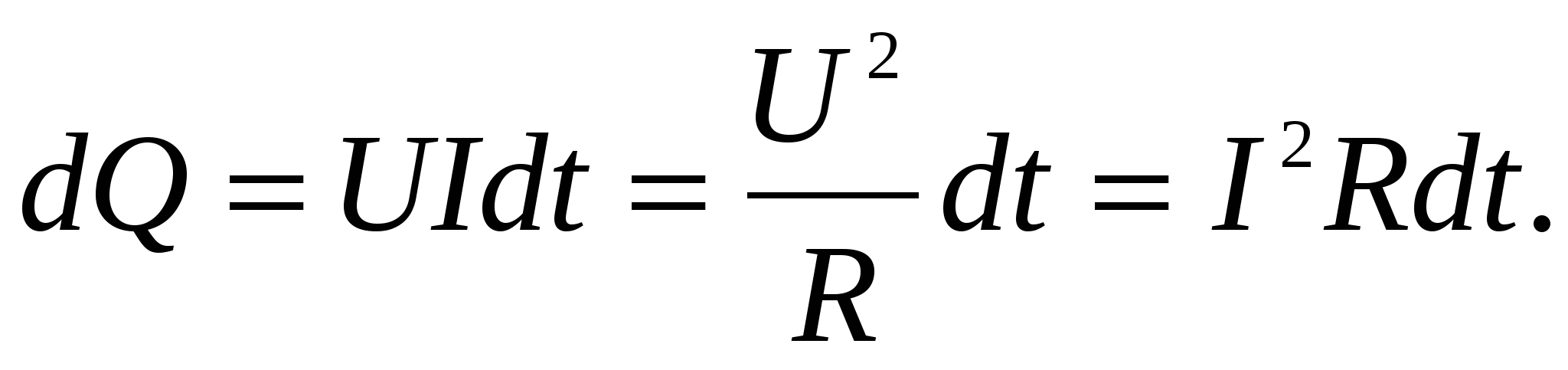
(2.17)Количество теплоты, выделяющееся за конечный промежуток времени от 0 до
t при прохождении постоянного тока силой
Iнайдем, интегрируя выражение (2.17):
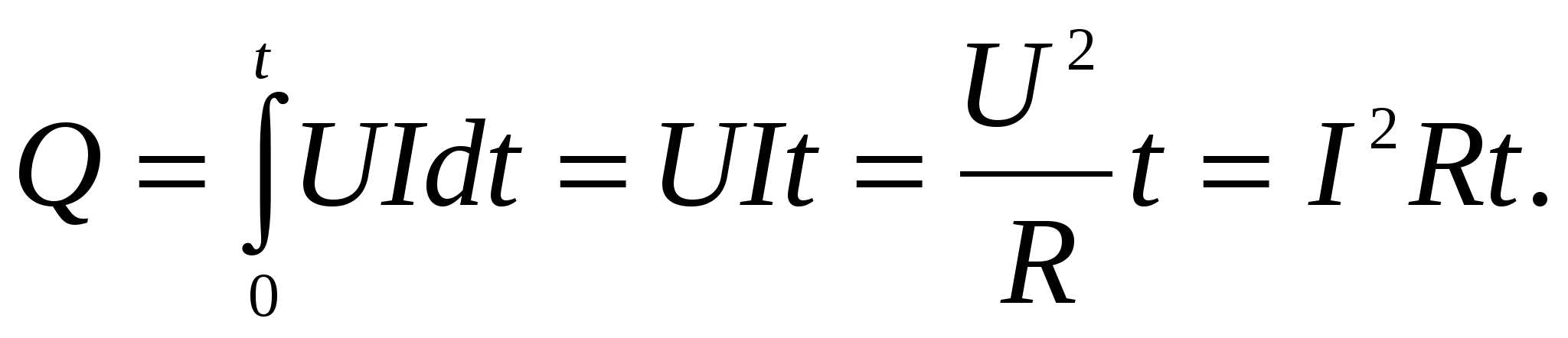
(2.18)
Выражение (2.18) есть закон Джоуля-Ленца для участка цепи постоянного тока.
Выделим в проводнике элементарный цилиндрический объем
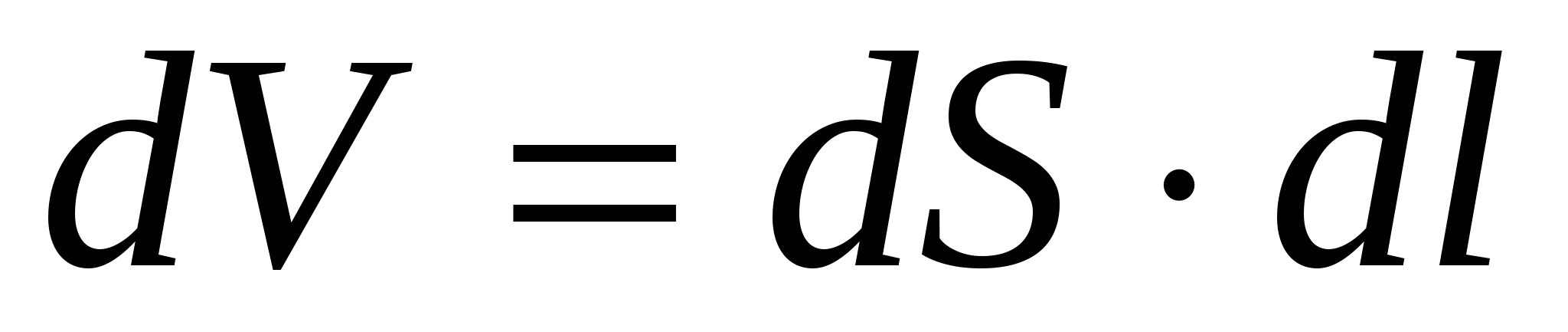
(ось цилиндра совпадает с направлением тока). Сопротивление этого элементарного объема
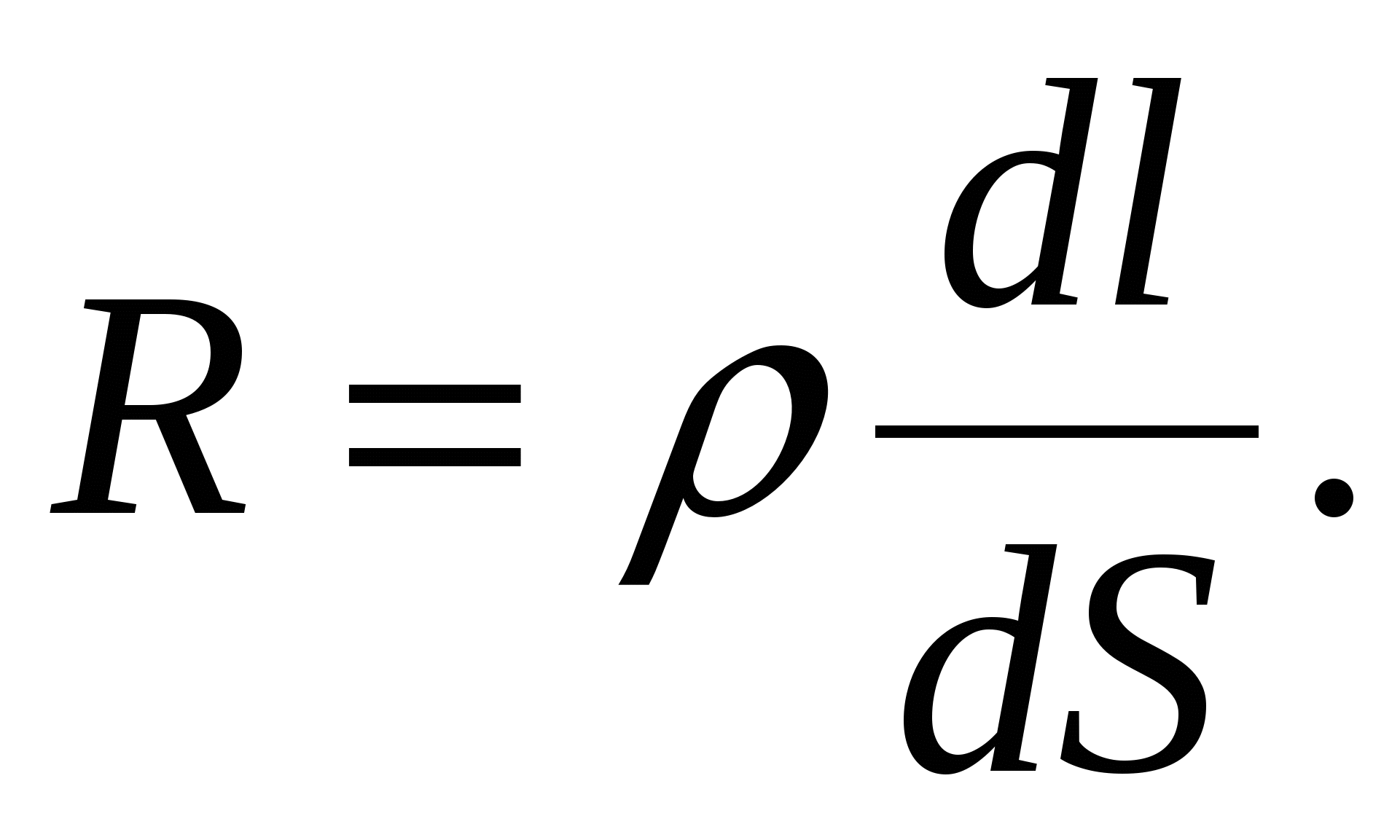
Тогда по закону Джоуля-Ленца за время
dt в этом объеме выделится теплота:
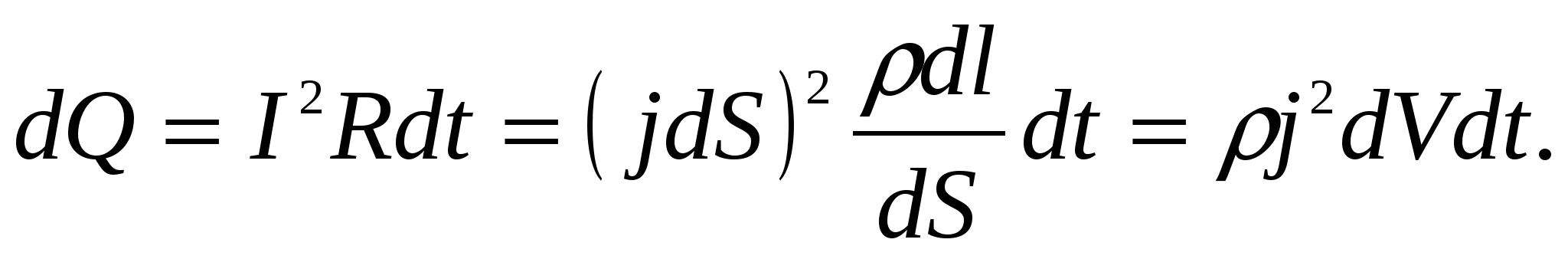
Количество теплоты, выделяющееся за единицу времени в единице объема, называется
удельной тепловой мощностью электрического тока:
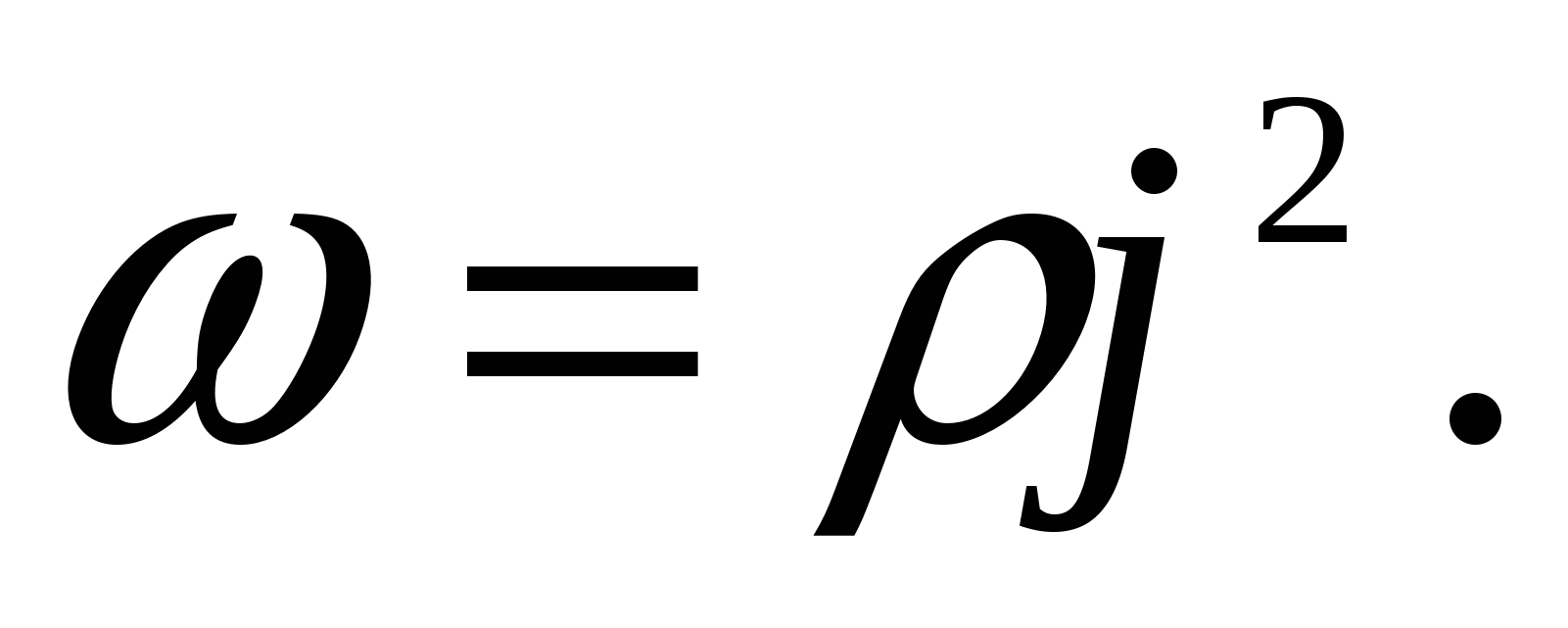
Используя дифференциальную форму закона Ома
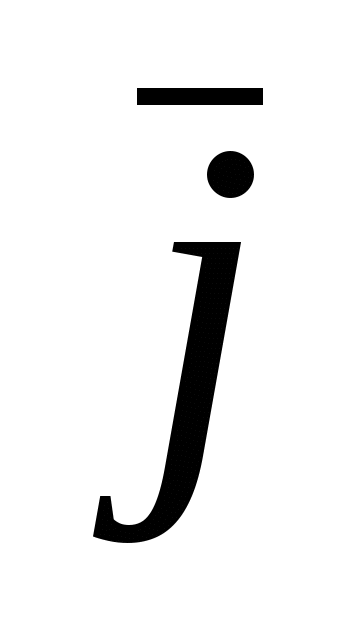
=δ
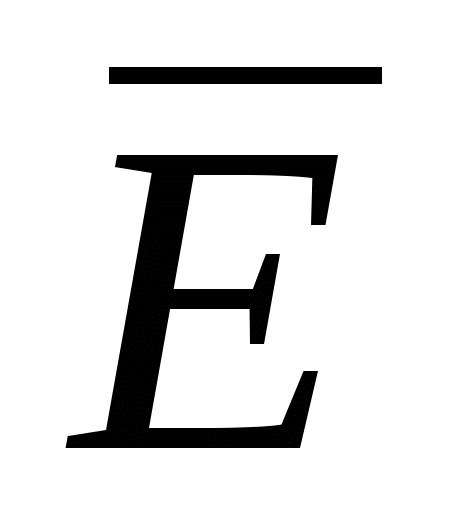
и соотношение
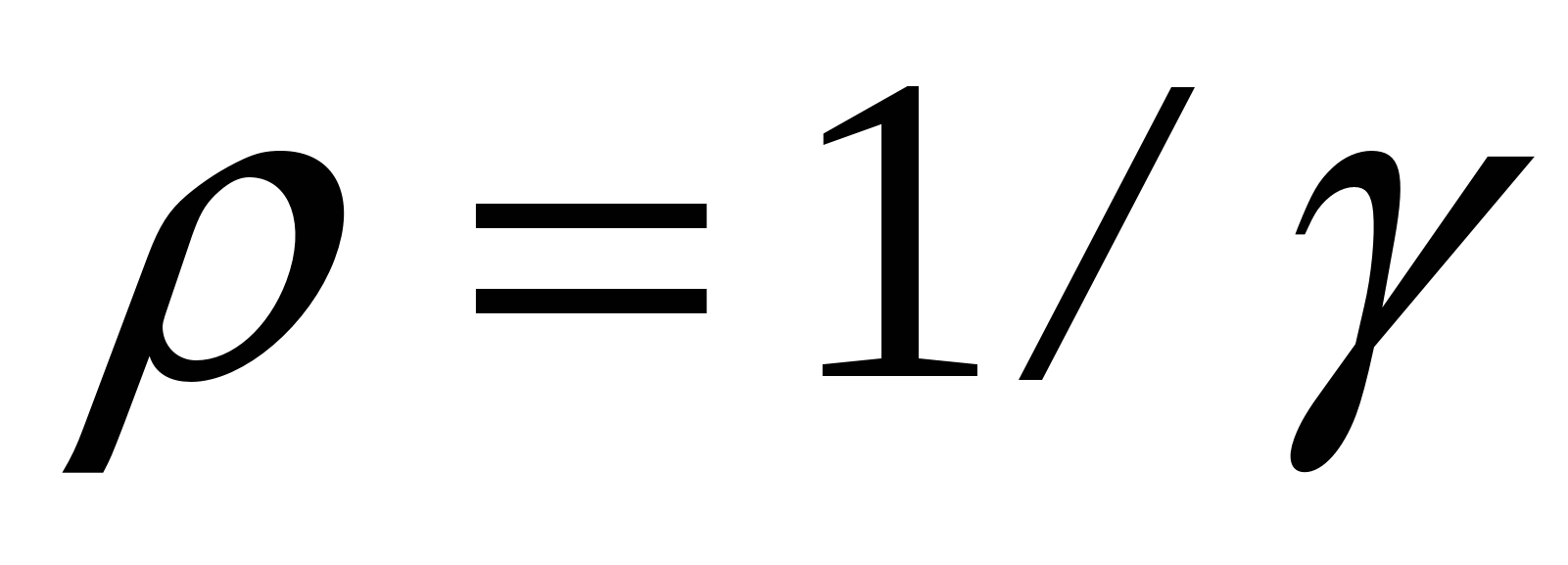
,получим:
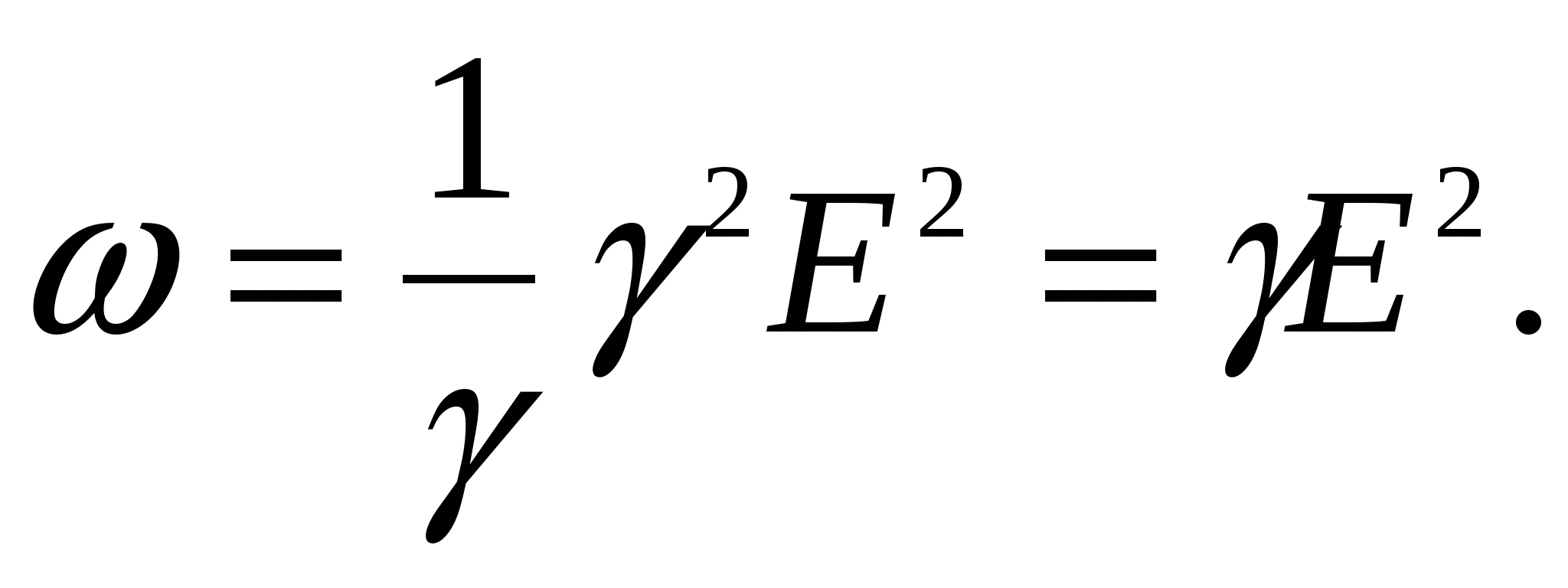
(2.19)Формула (2.19) является обобщенным выражением
закона Джоуля-Ленца в дифференциальной форме, пригодным для любого проводника.
ЗАКОН ОМА В ИНТЕГРАЛЬНОЙФОРМЕД
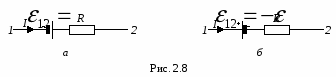
+
ля однородного участка цепи, т.е. для участка, на котором не действуют сторонние силы, закон Ома записывается в форме
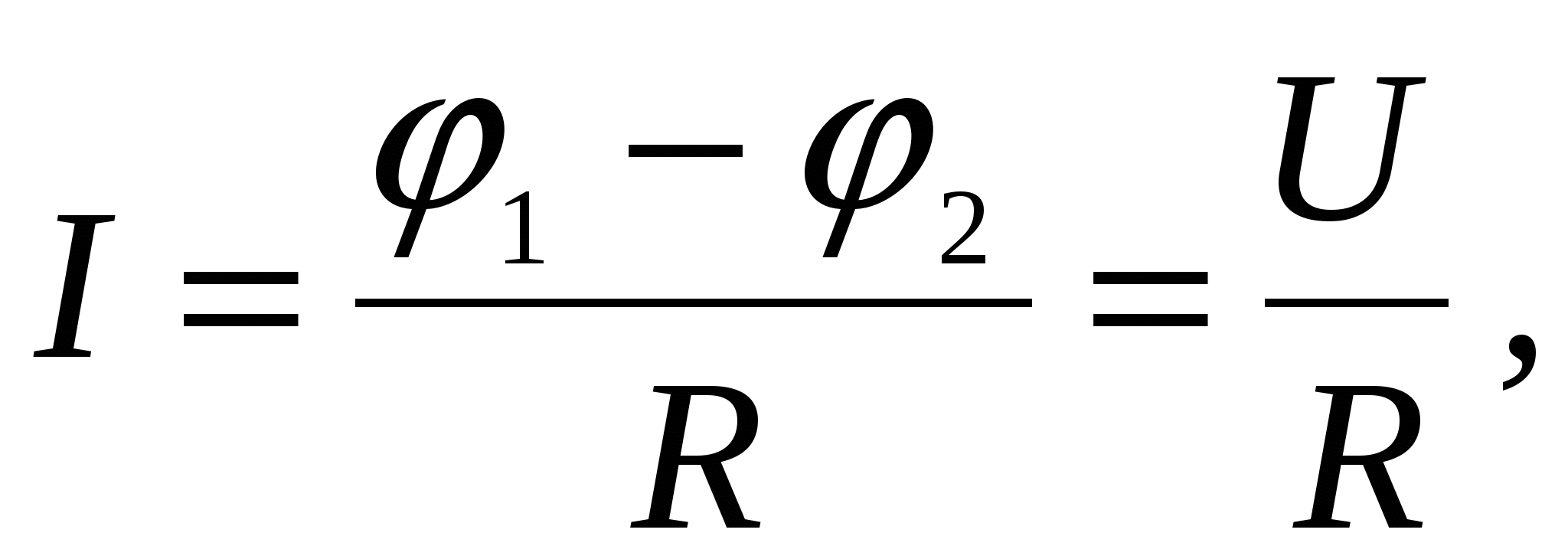
. Рассмотрим теперь
неоднородный участок цепи 1-2 (рис. 2.8), где действует ЭДС источника
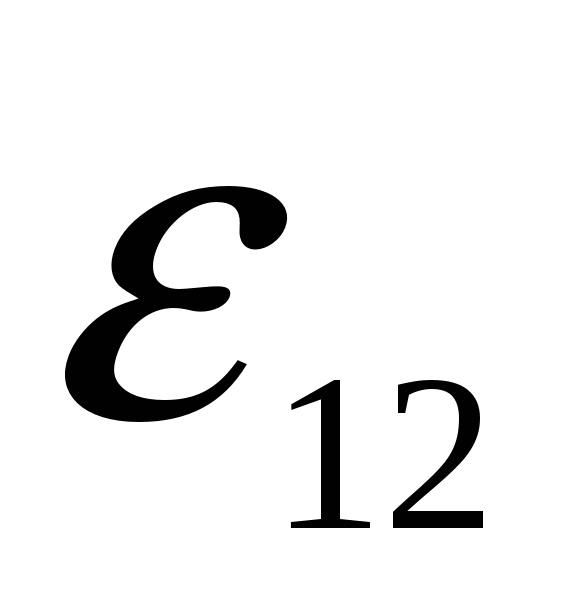
и на концах которого приложена разность потенциалов
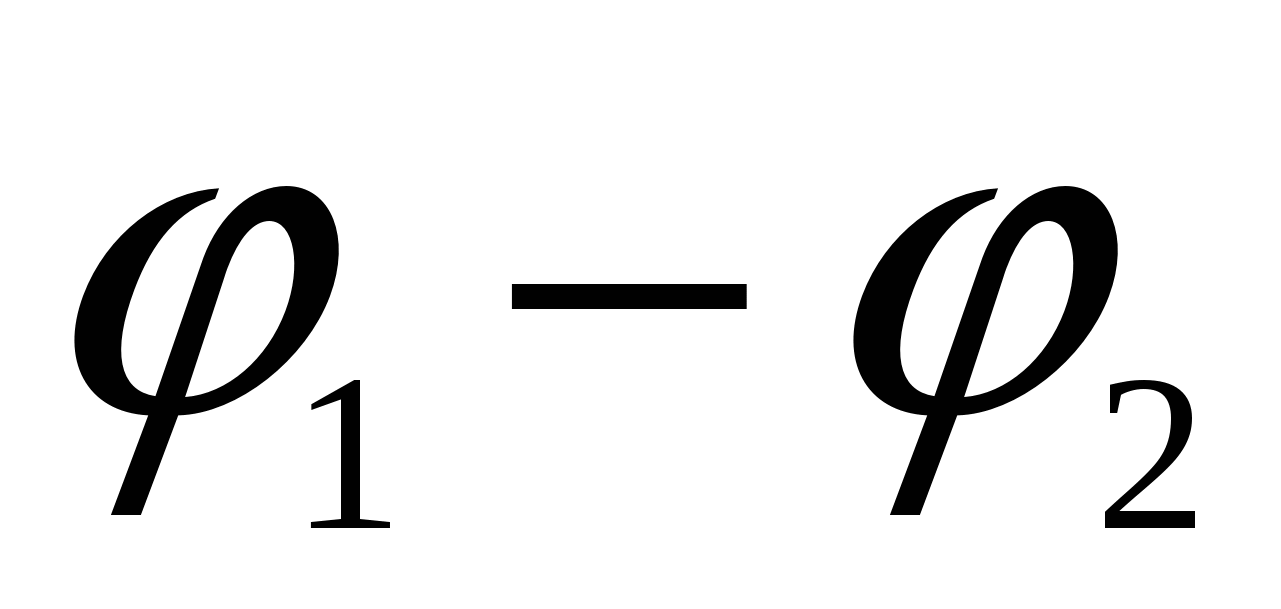
.
На рассматриваемом участке работа

всех приложенных сил (сторонних и электростатических), совершаемая над носителями тока, согласно (2.6) равна:
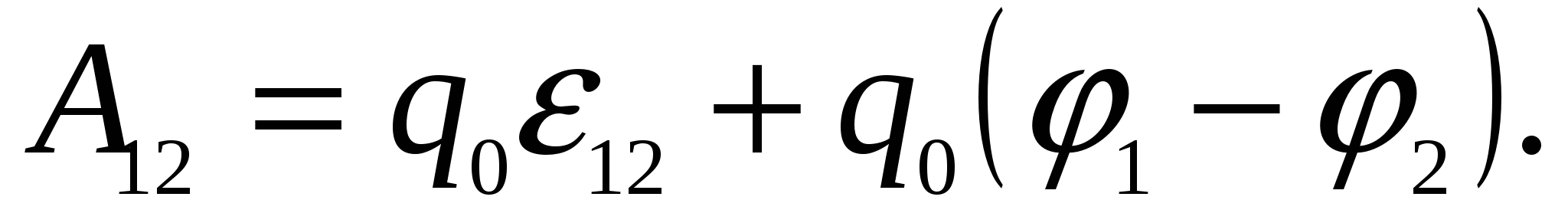
В
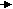
этой формуле ЭДС
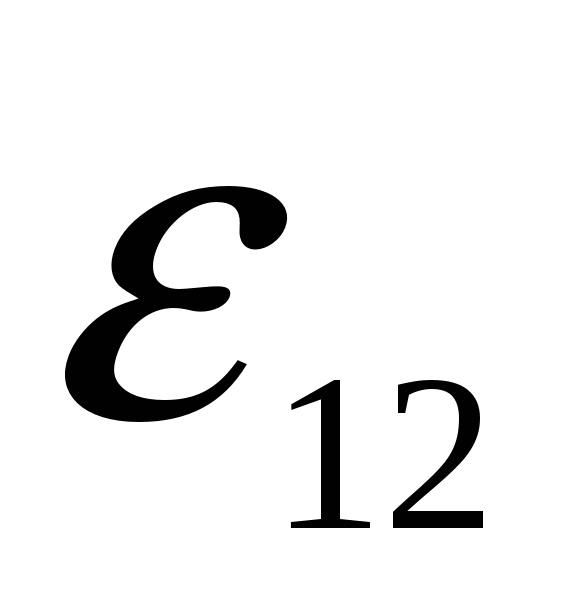
берется либо с положительным, либо с отрицательным знаком. Если ЭДС способствует движению положительных зарядов в направлении обхода (в направлении 1-2), т.е. внутри источника обход совпадает с перемещением зарядов от катода к аноду, то
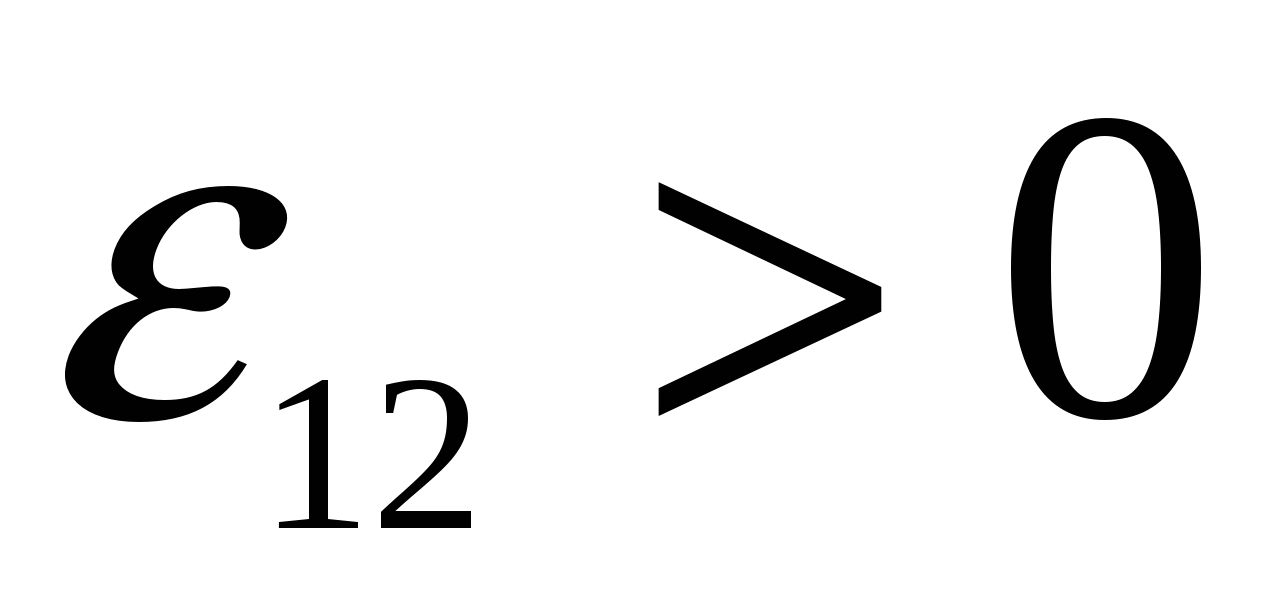
(рис. 2.8,
а). Если ЭДС препятствует движению положительных зарядов в направлении обхода, то
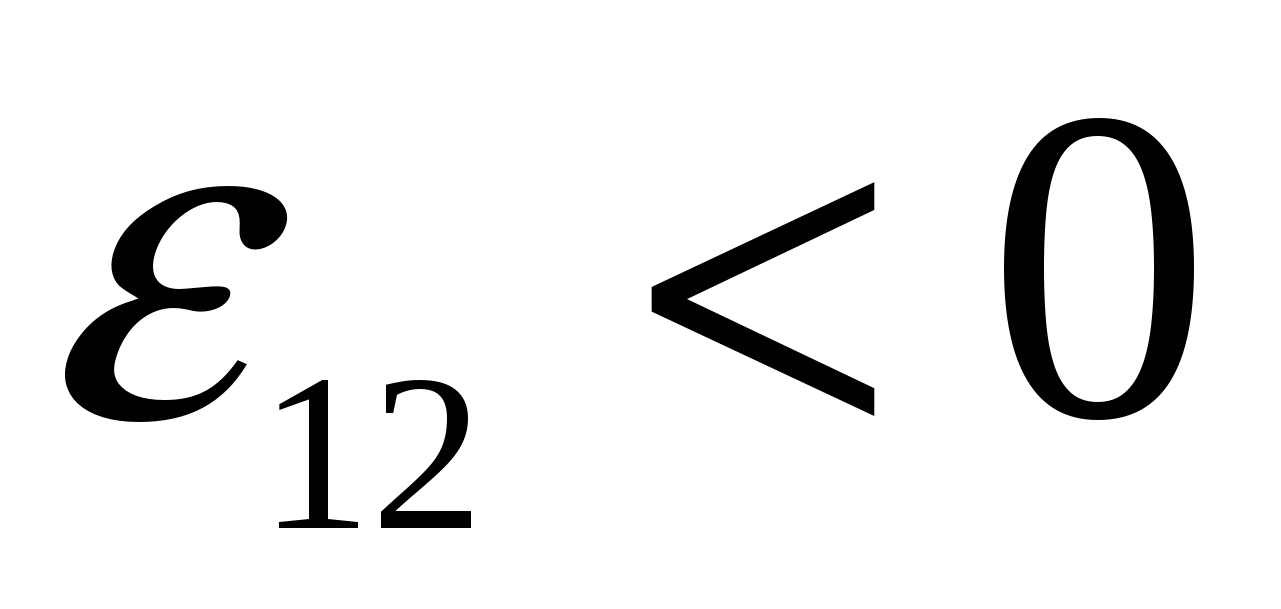
(рис. 2.8,
б).
По закону сохранения и превращения энергии работа

равна теплоте, выделяющейся на участке 1-2 за время
t (эта теплота определяется согласно закону Джоуля-Ленца):
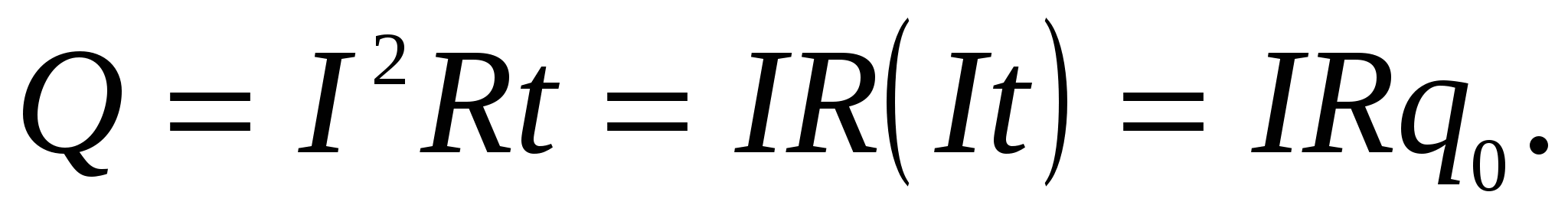
(2.20)Приравнивая (2.6) и (2.20), получим:
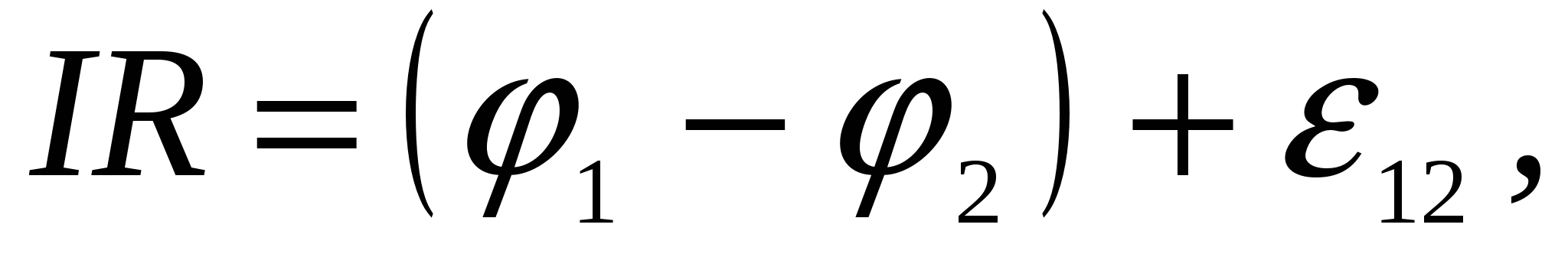
(2.21)или
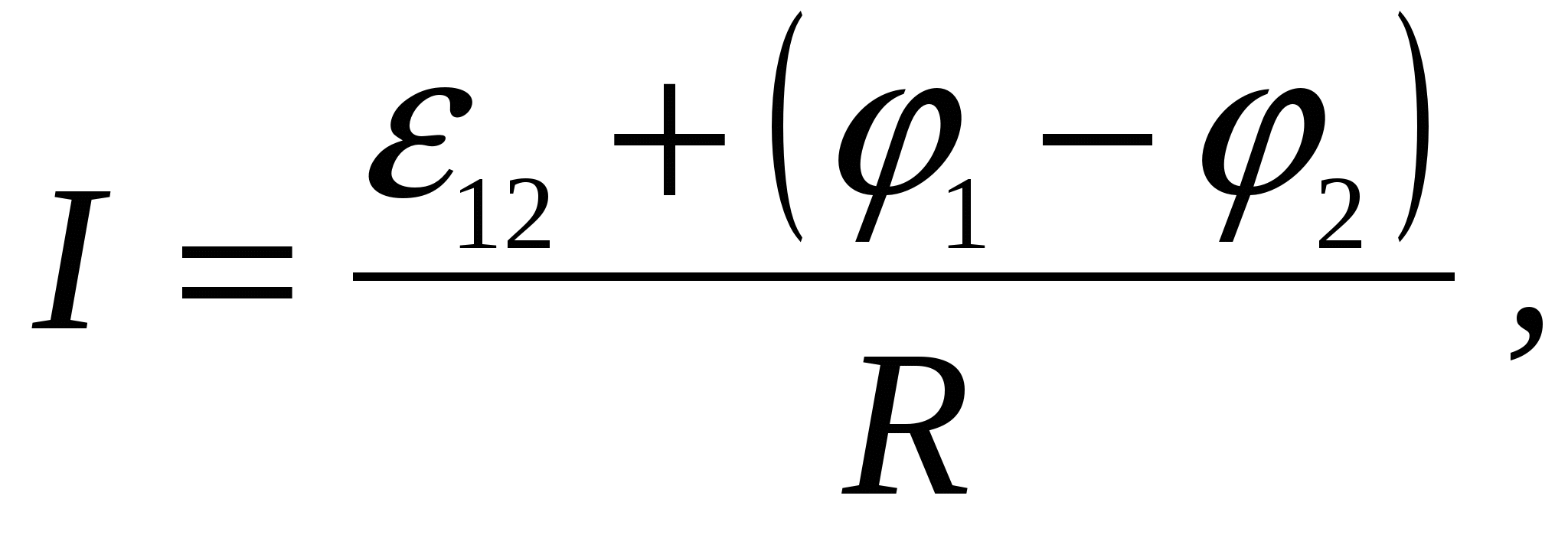
(2.22)где
R– суммарноесопротивление, включающее в себя внутреннее сопротивление
r источника тока и сопротивление внешней цепи.Выражение (2.21) или (2.22) есть
закон Ома в интегральной (обобщенной) форме для цепи постоянного тока.Действительно, если на данном участке цепи
источник тока отсутствует (
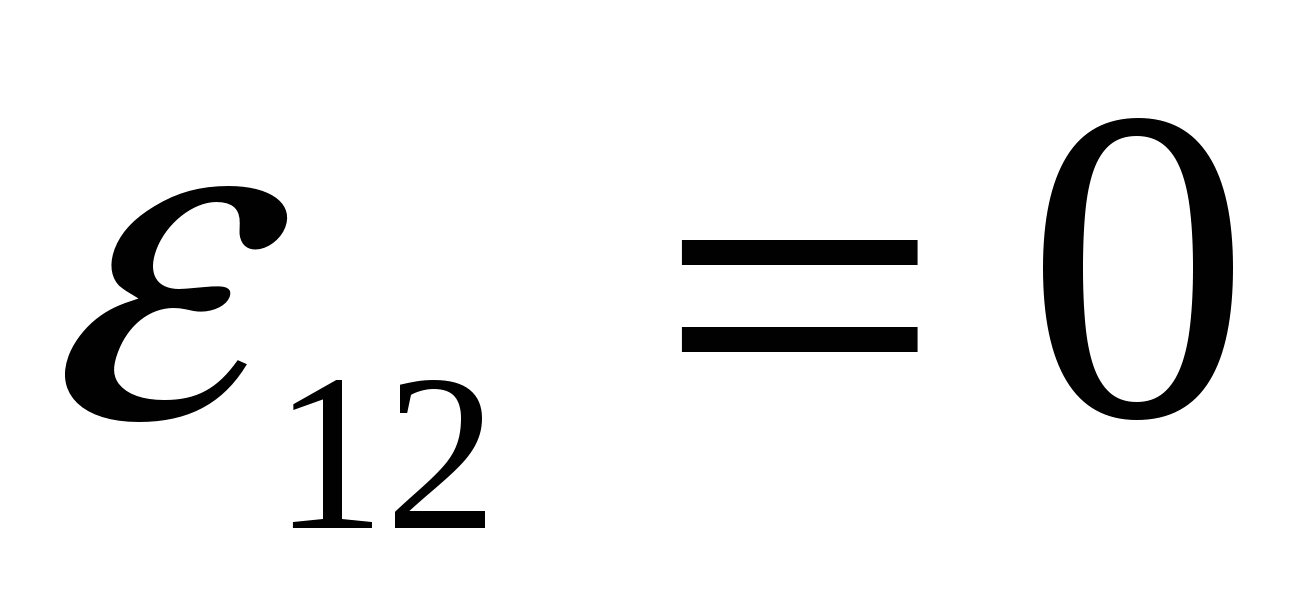
), то из (2.22) приходим к закону Ома для однородного участка цепи:
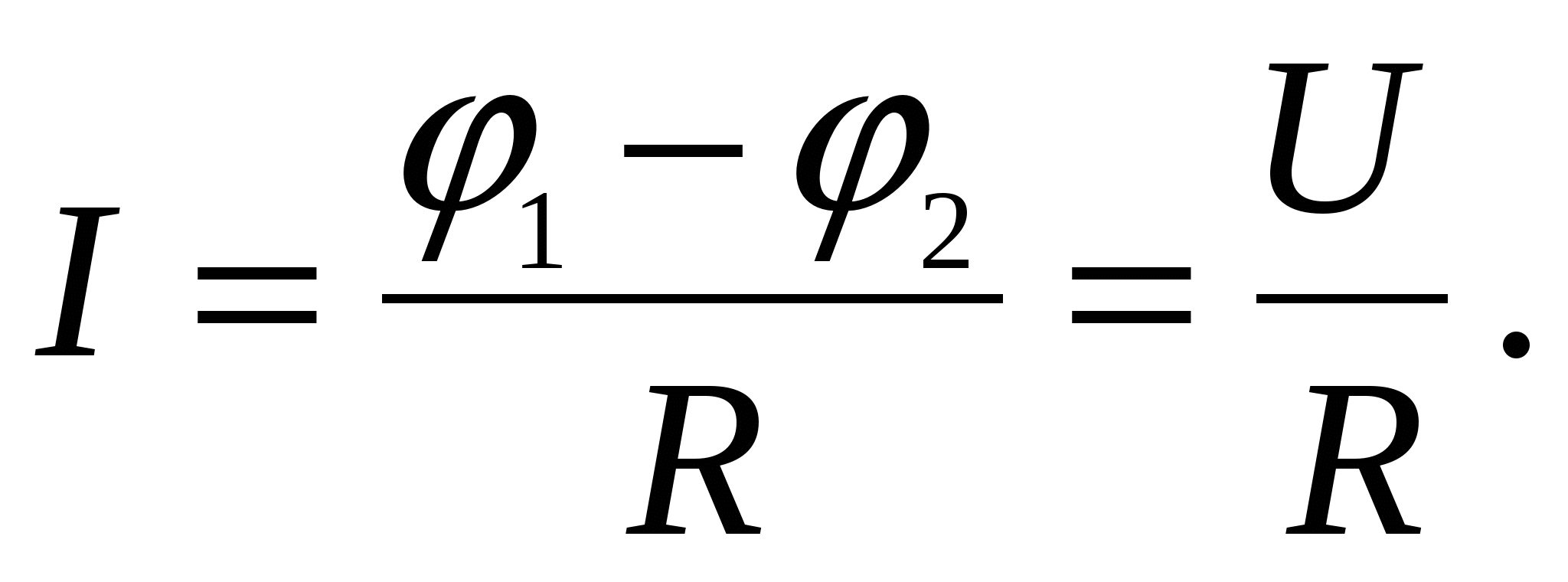
Если электрическая
цепь замкнута (точки 1 и 2 совпадают), то
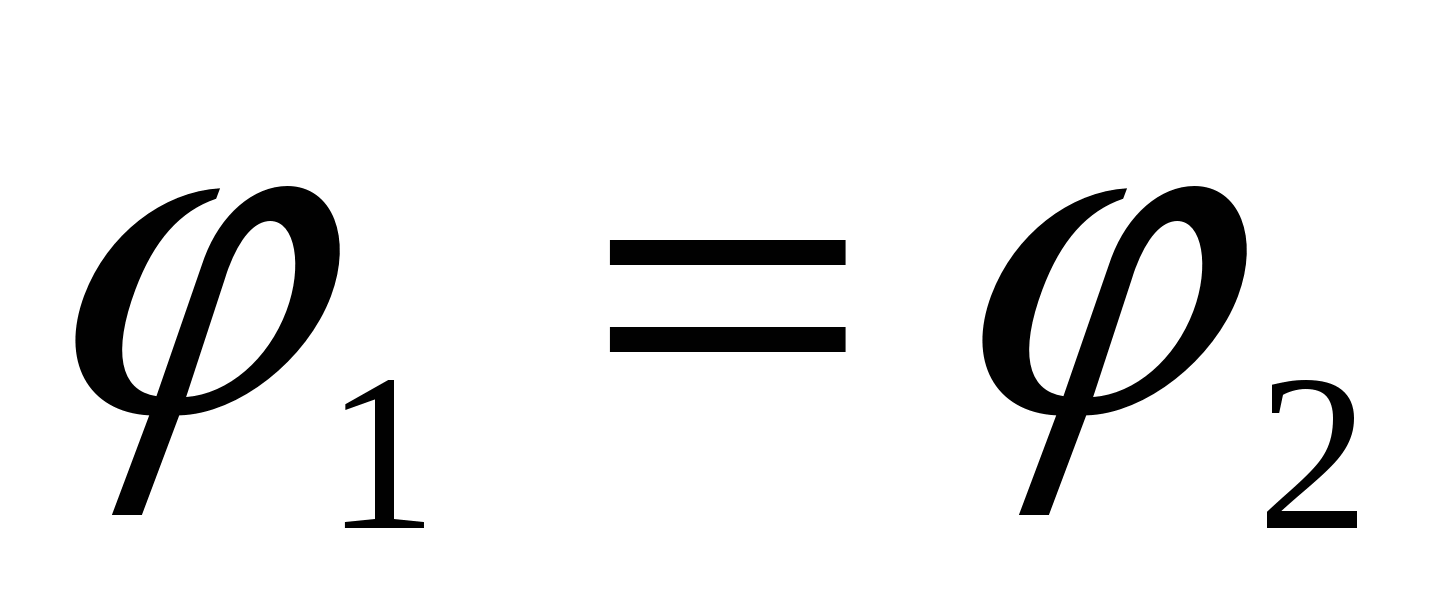
. Тогда из (2.22) получаем
закон Ома для замкнутой цепи:
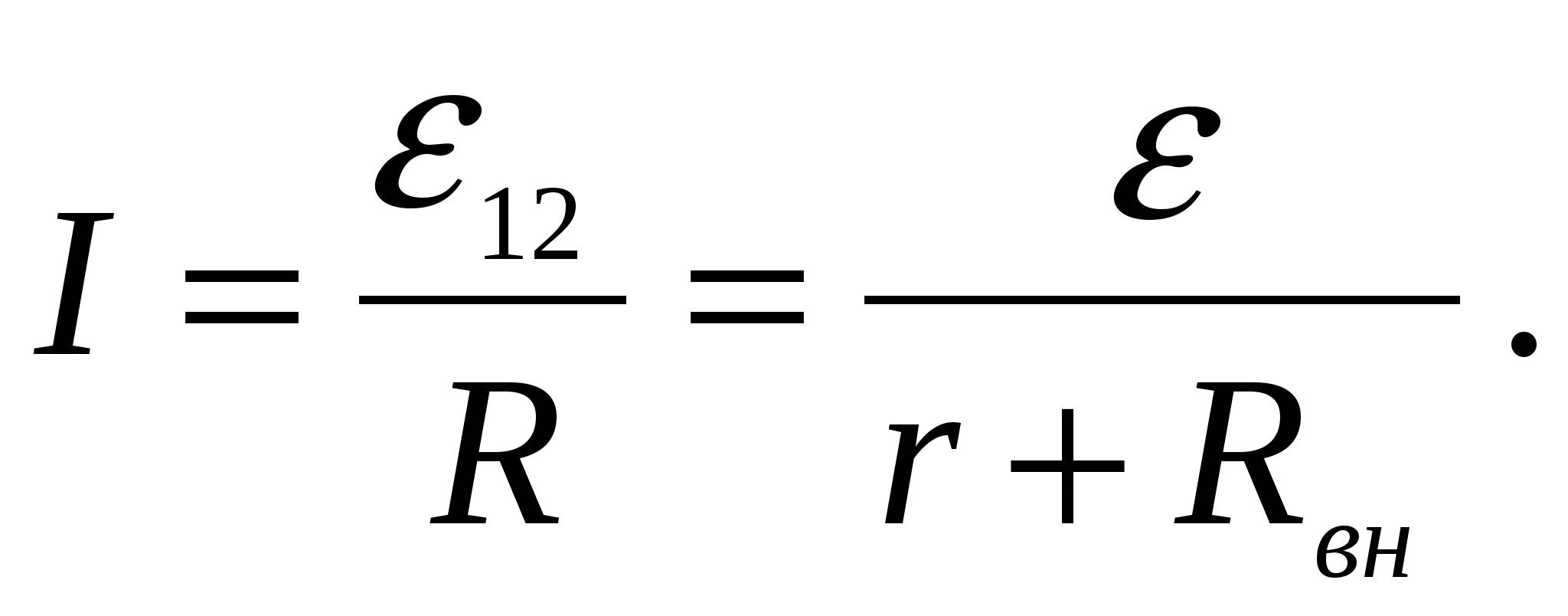
Наконец, если
цепь разомкнута, то
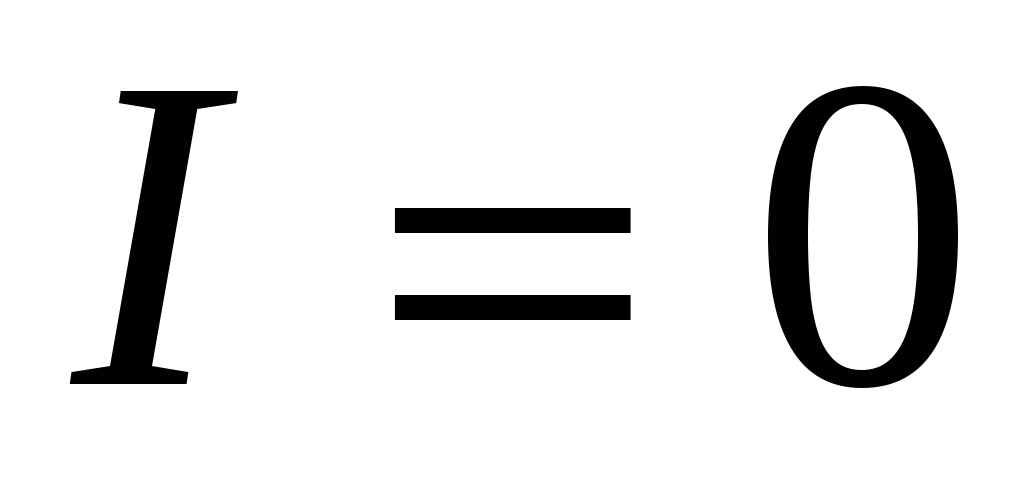
и из (2.22) получаем, что
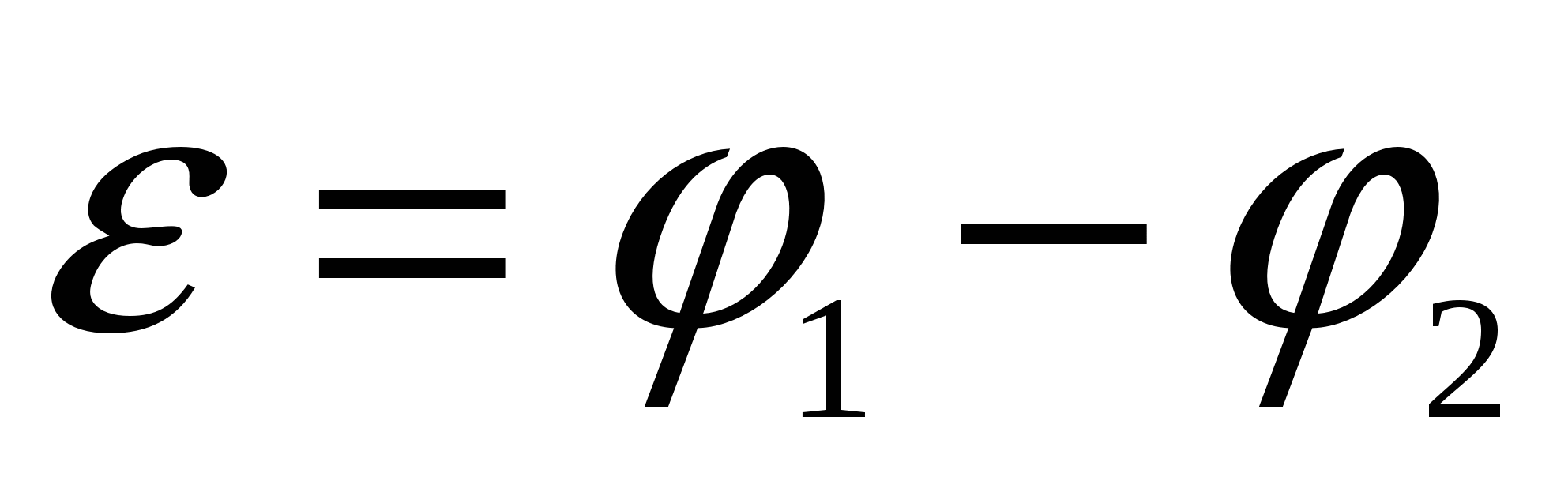
, следовательно, для экспериментального определения ЭДС источника тока необходимо измерить разность потенциалов на его зажимах при разомкнутой нагрузке (
режим холостого хода цепи).
ПОСЛЕДОВАТЕЛЬНОЕ И // СОЕДИНЕНИЕ ПРОВОДНИКОВ Электрическая цепь представляет собой совокупность различных проводников и источников тока. В общем случае цепь является разветвленной и содержит участки, где проводники могут соединяться последовательно и параллельно.
При последовательном соединении проводников :
а) сила тока во всех частях цепи одинакова (
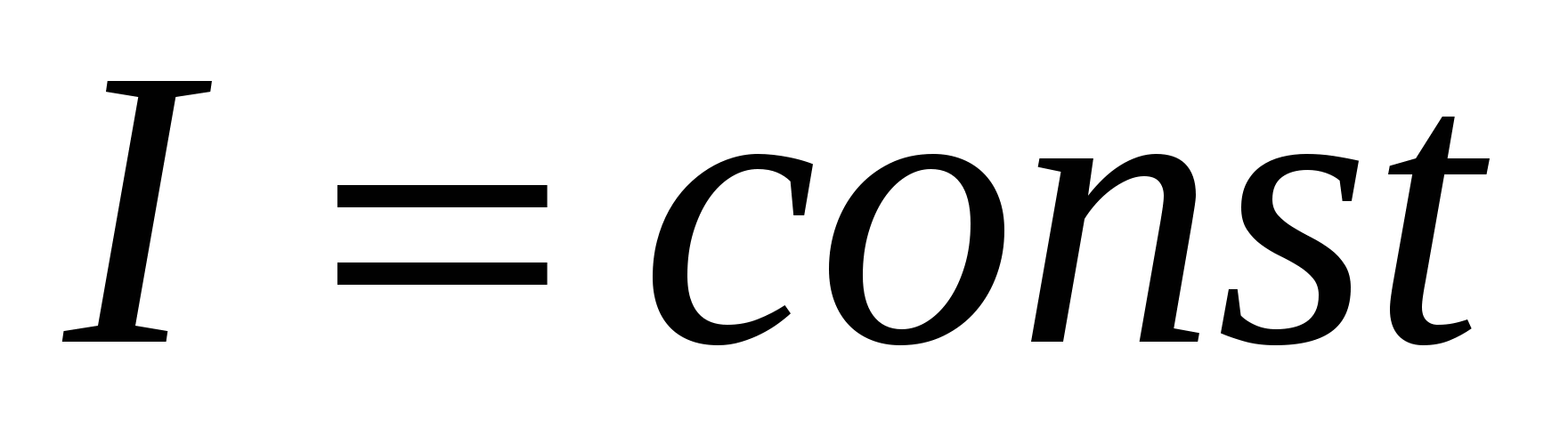
);
б) напряжение на зажимах цепи равно сумме падений напряжений на отдельных участках (
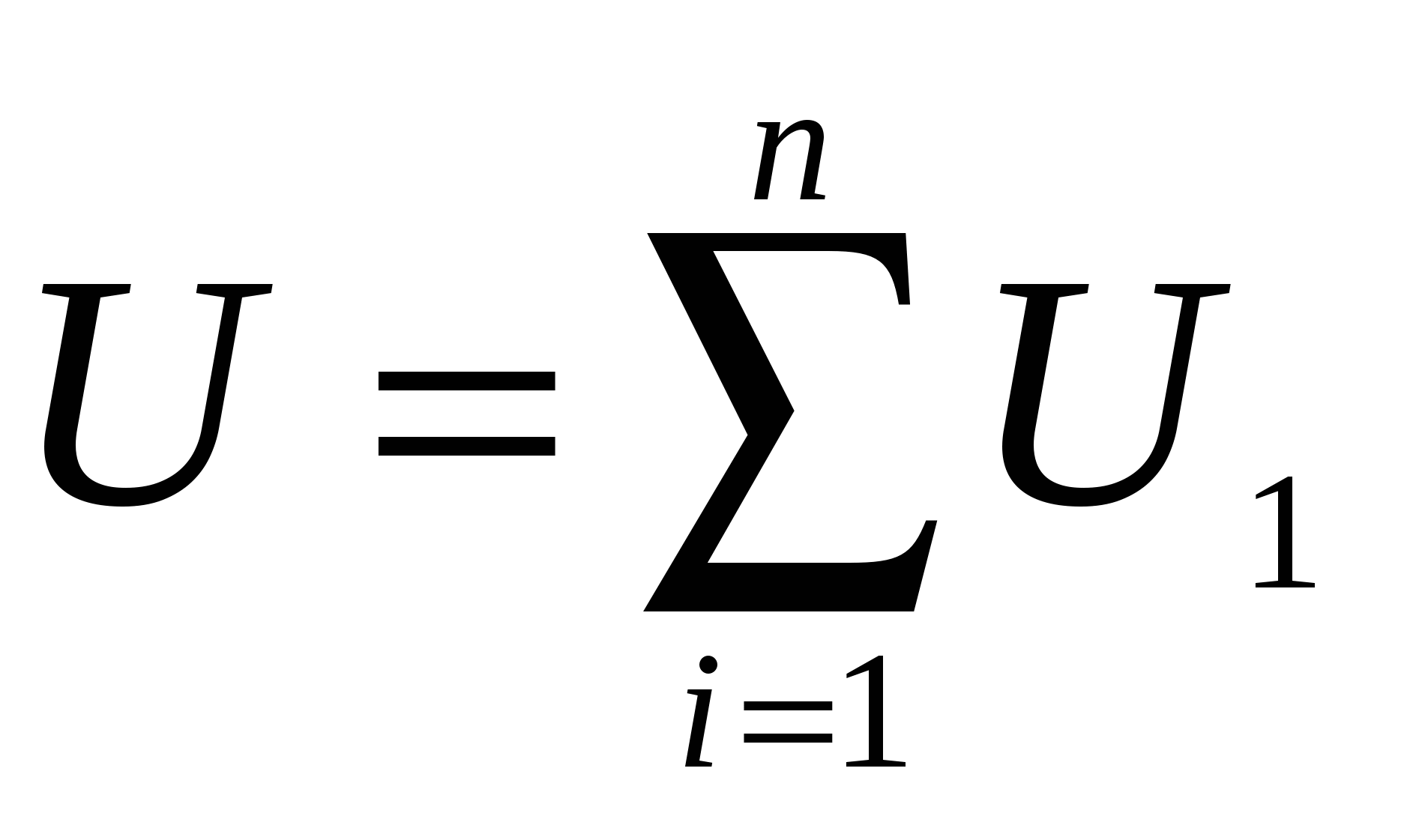
).Учитывая эти положения и используя закон Ома для однородного участка, найдем общее (эквивалентное) сопротивление цепи:
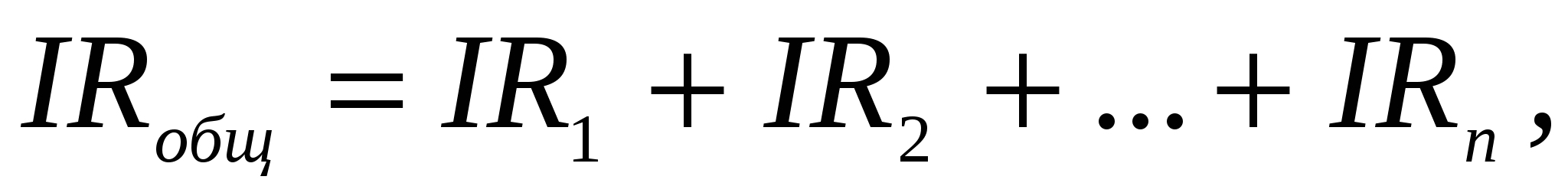
или
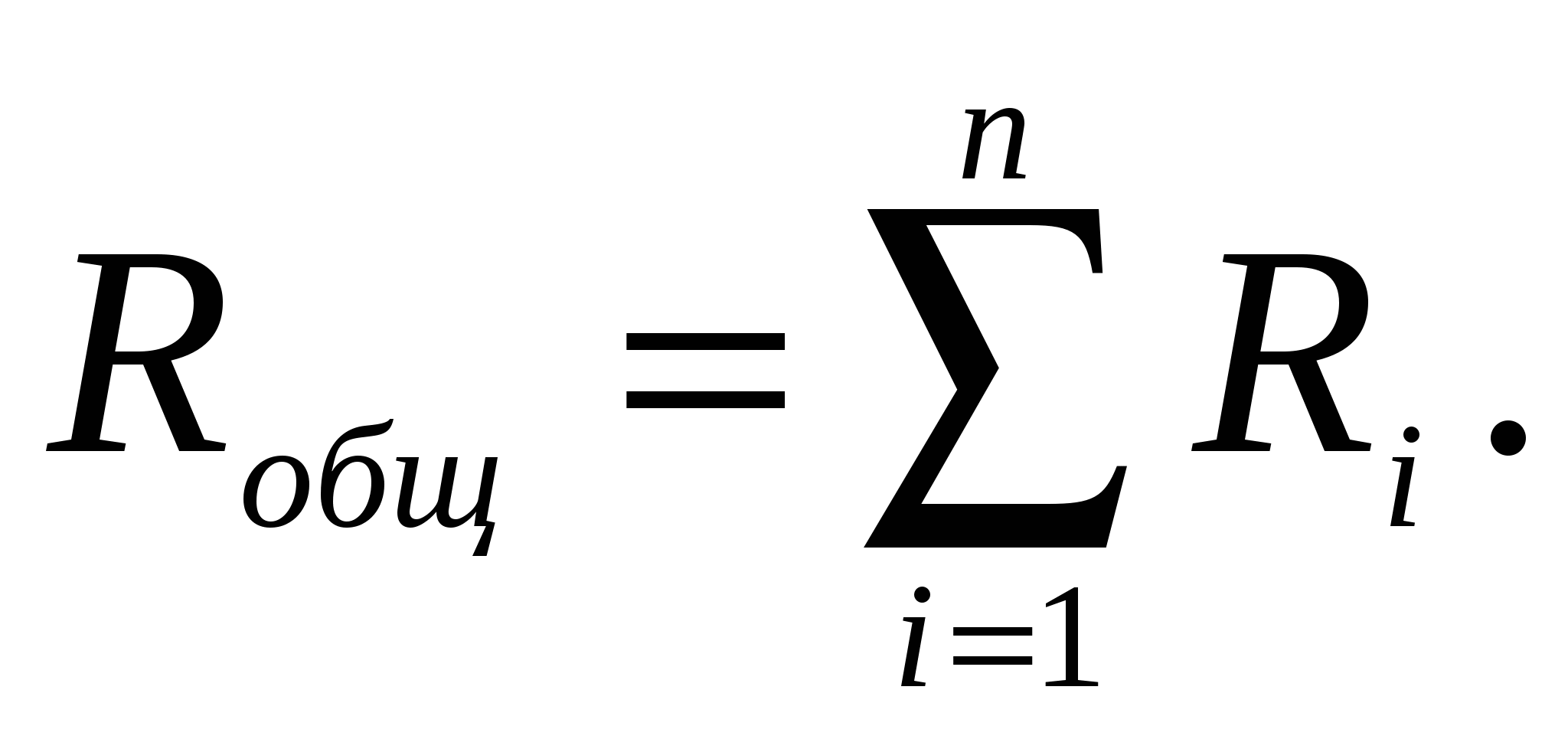
(2.12)Таким образом,
общее сопротивление цепи, состоящей из последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников.При параллельном соединении проводников (рис. 2.3,
б):а) сила тока в неразветвленной части цепи равна сумме сил токов, протекающих в разветвленных участках цепи (
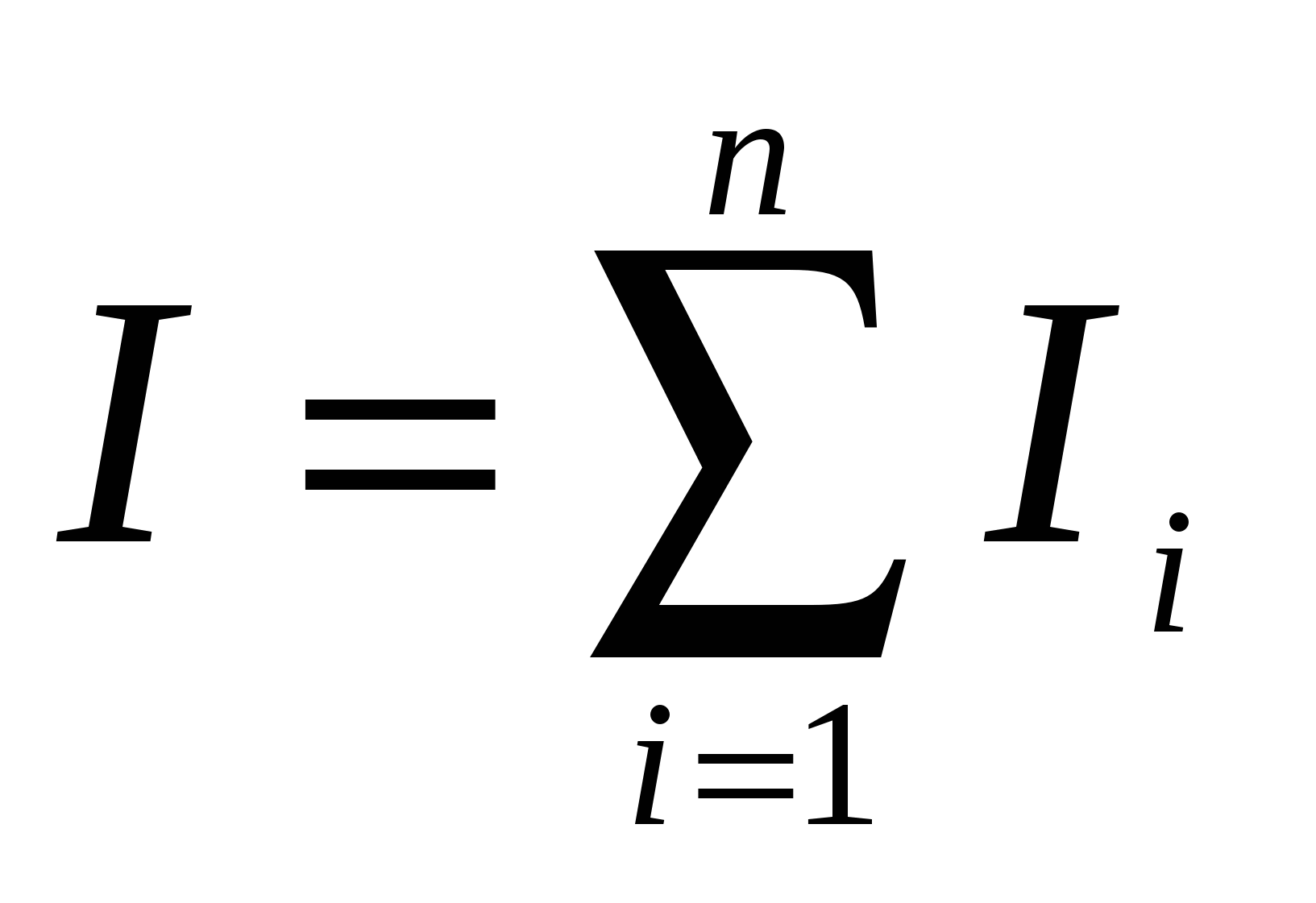
);
б) падения напряжения в параллельно соединенных участках цепи одинаковы и равны напряжению на зажимах цепи (
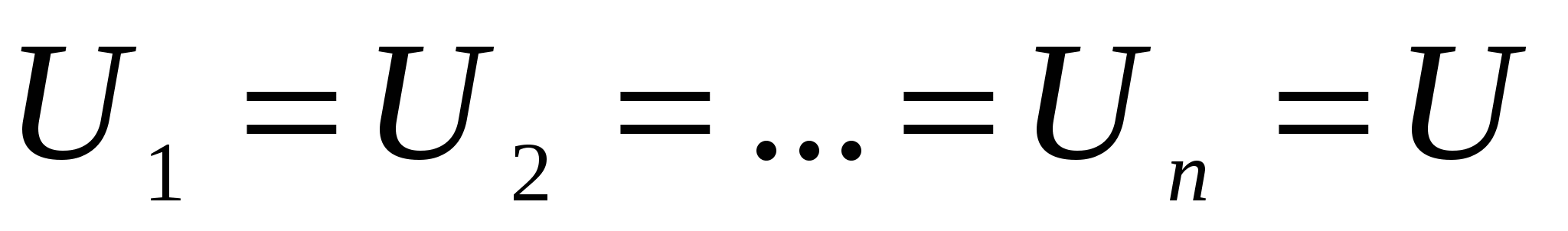
).
С учетом этих положений и на основании закона Ома для однородного участка цепи найдем общее (эквивалентное) сопротивление цепи:
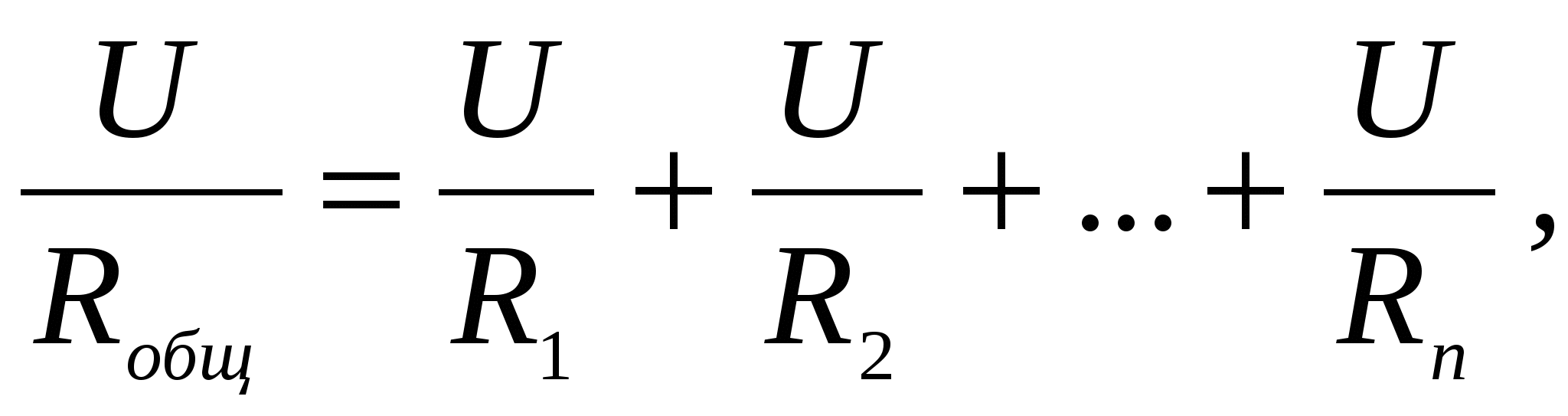
или
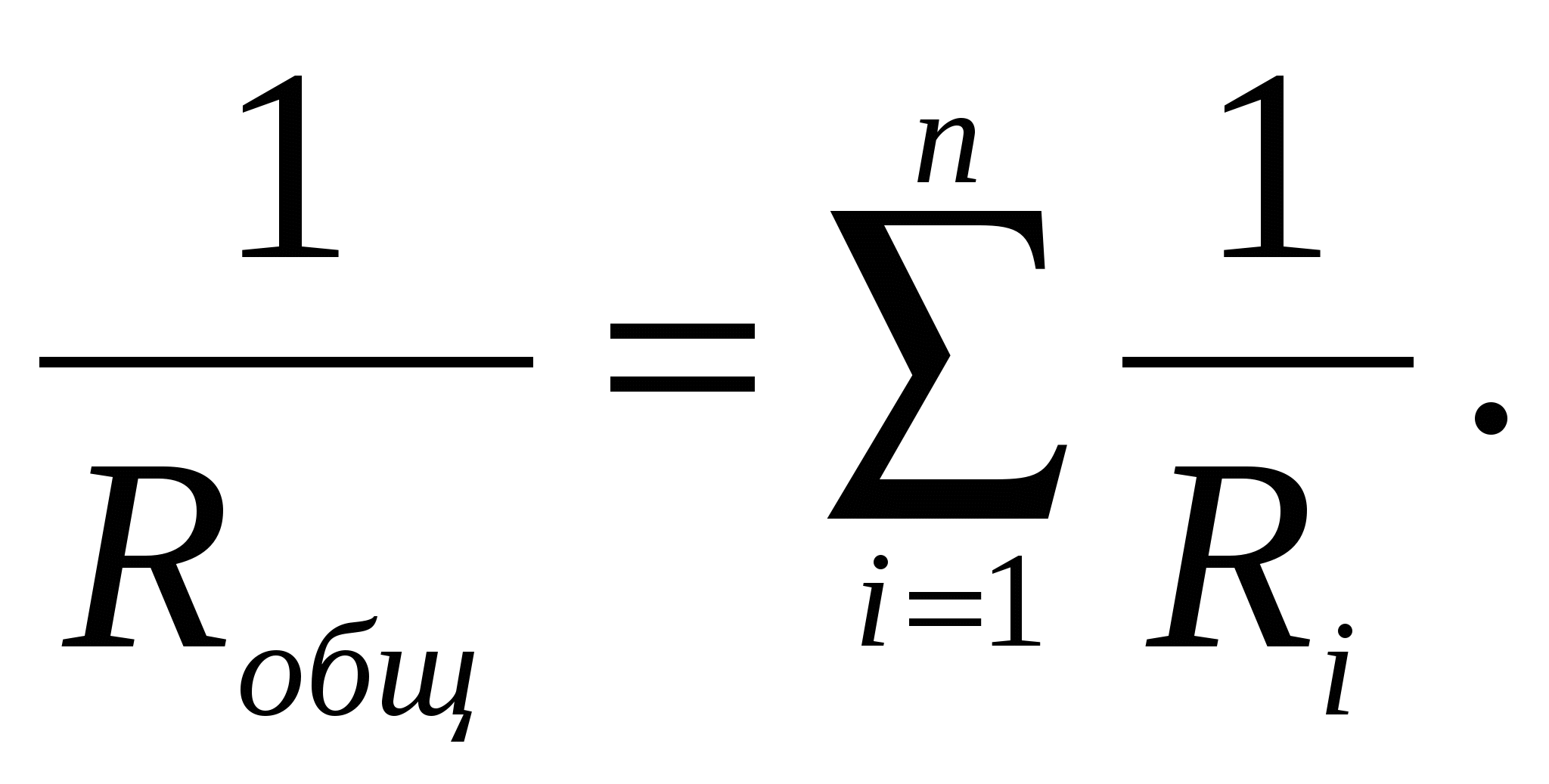
(2.13)Таким образом,
при параллельном соединении проводников складываются величины, обратные сопротивлениям отдельных участков цепи (проводимости ветвей).
РАСЧЁТ РАЗВЕТВЛЁННОЙ ЦЕПИ.ПРАВИЛО КИРХГОФАЛ
юбая точка разветвленной электрической цепи, в которой сходится не менее трех проводников тока, называется
узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла – отрицательным (рис. 2.9).
Первое правило Кирхгофа сформулировано для узла электрической цепи:
алгебраическая сумма сил токов в узле электрической цепи равна нулю, т.е.
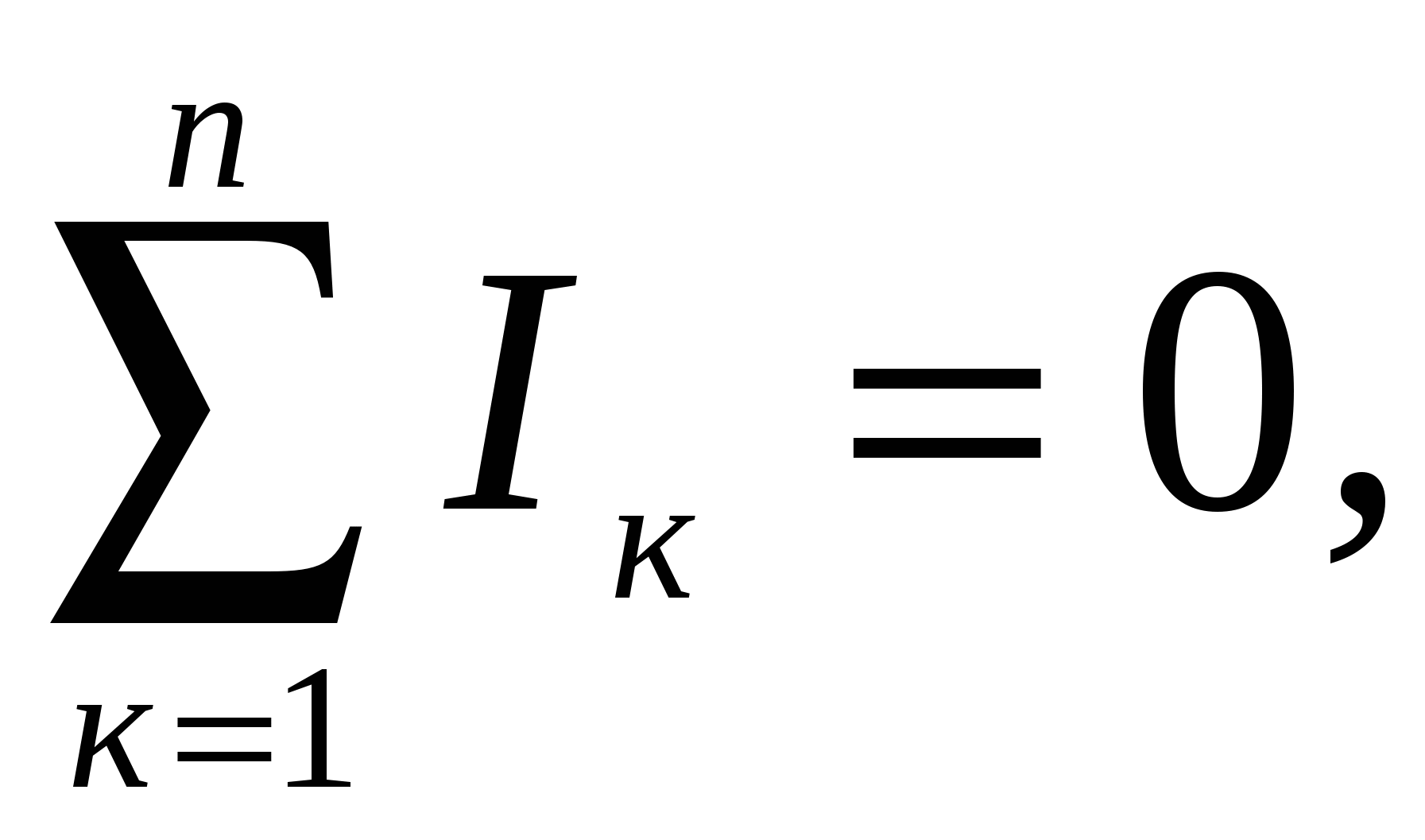
где
n- число проводников, сходящихся в узле.Таким образом, при указанных на рис. 2.9 направлениях токов в проводниках первое правило Кирхгофа запишется в виде
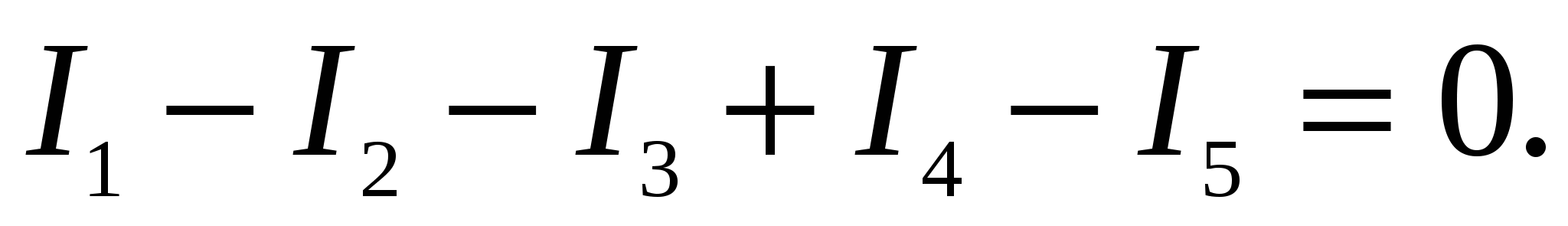
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
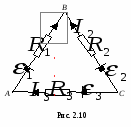
Второе правило Кирхгофа вытекает из закона Ома в интегральной форме для разветвленных цепей. Выделим в сложной электрической цепи замкнутый контур, состоящий из трех участков (рис. 2.10). Условимся обходить контур по часовой стрелке. Все токи, совпадающие по направлению с выбранным направлением обхода контура, считаются положительными. ЭДС источников считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к отдельным участкам контура закон Ома, запишем:
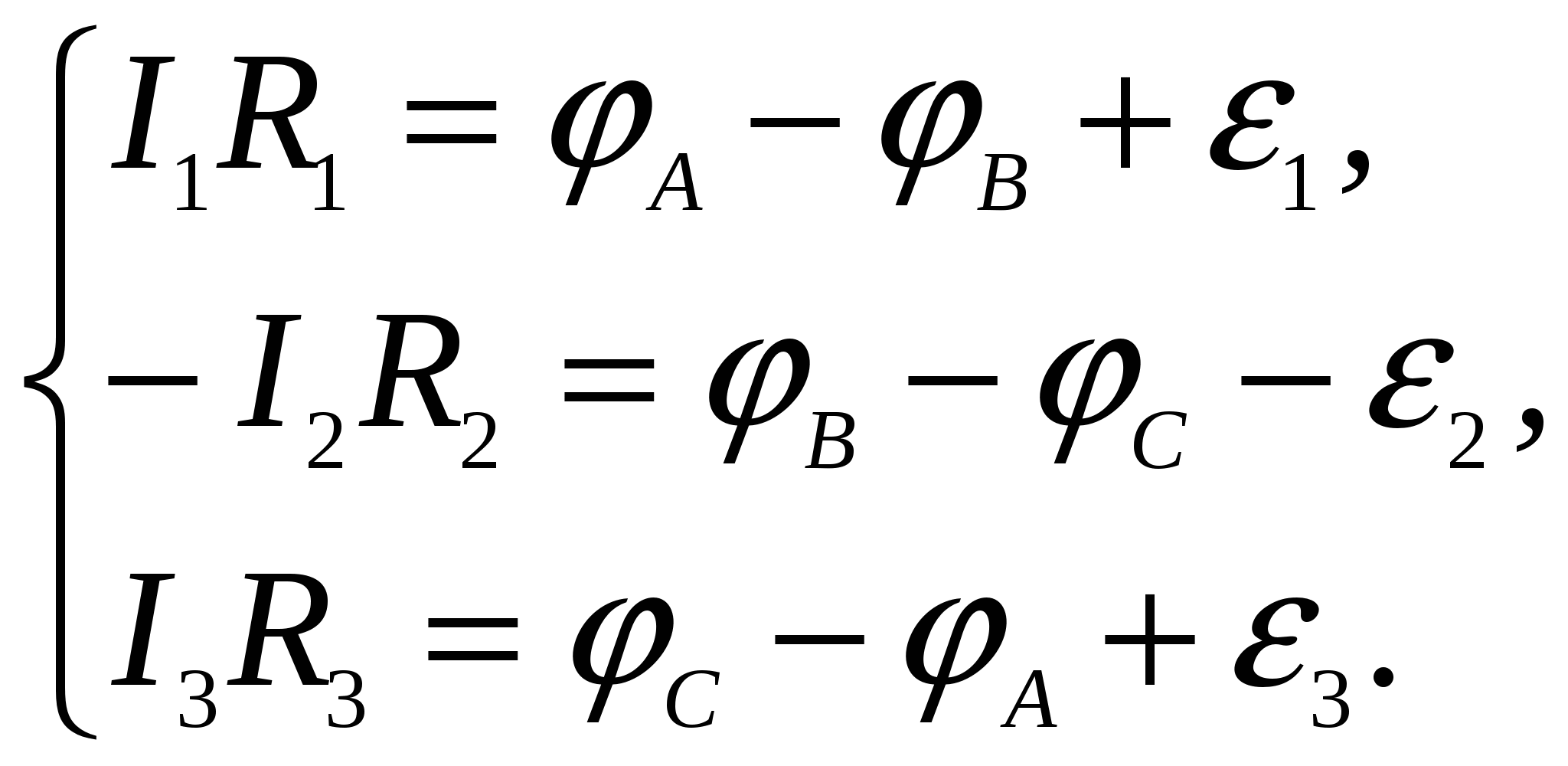
Складывая почленно эти уравнения, получим:
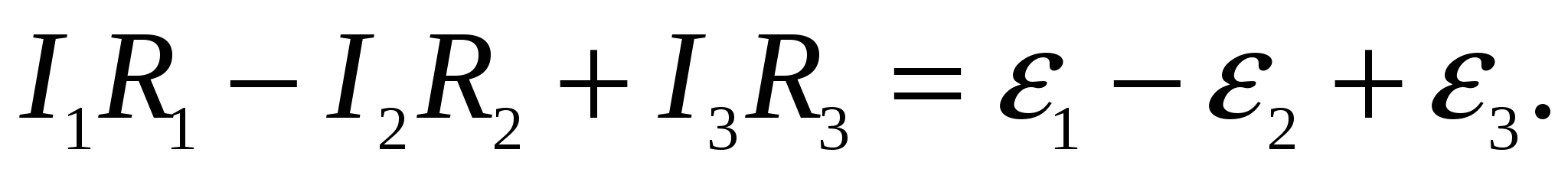
Второе правило Кирхгоф:
в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС источников равна алгебраической сумме падений напряжений на отдельных участка этого контура, т.е.
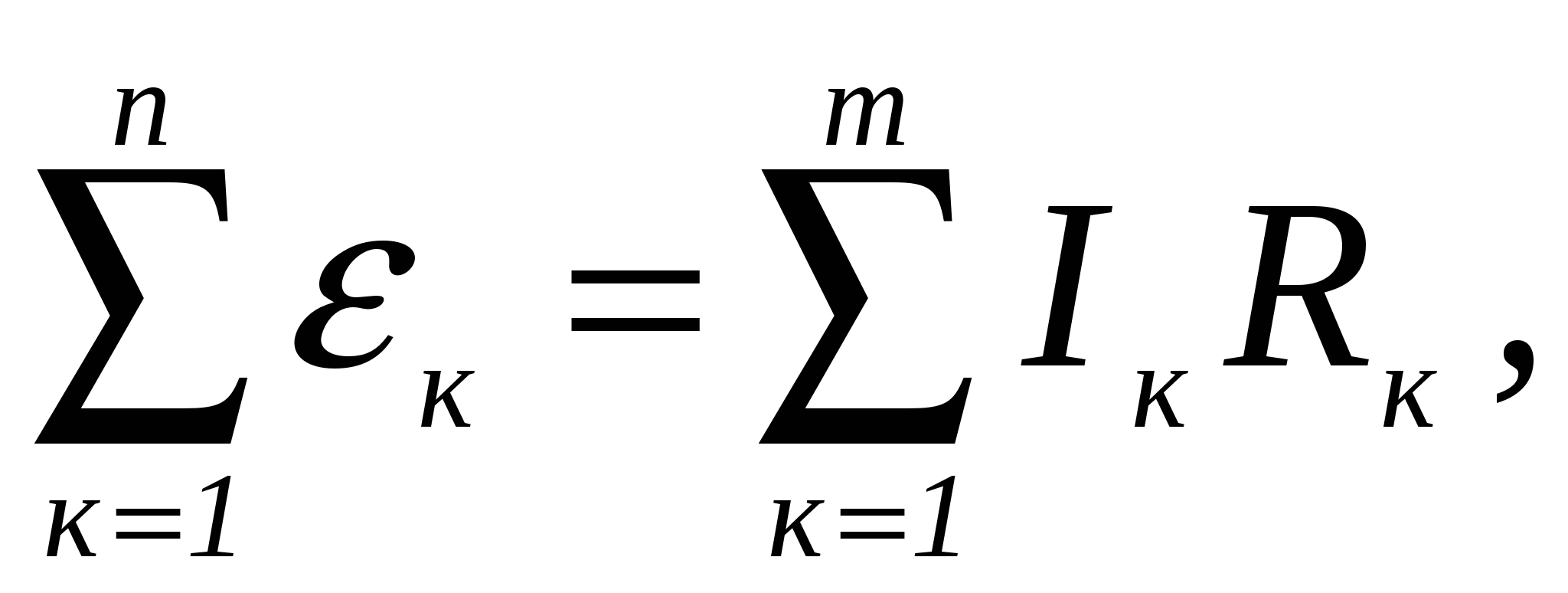
где
n – количество источников тока в контуре;
m – число участков в контуре.
МАГНИТНОЕ ПОЛЕ И ЕГО ХАРАКТЕРИСТИКИ
Опыт показывает, что подобно тому, как в пространстве, окружающем электрические заряды, возникает электрическое поле (являющееся средой взаимодействия между ними), так в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое
магнитным. Наличие такого поля обнаруживается по силовому воздействию на внесенные в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием силового поля, создаваемого током. При пропускании по прямолинейному горизонтальному проводнику постоянного тока силой
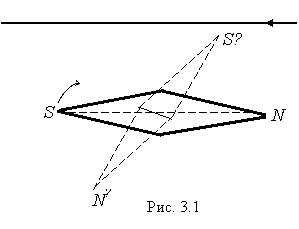
I находящаяся под ним магнитная стрелка поворачивается вокруг своей вертикальной оси, стремясь расположиться перпендикулярно проводнику с током. Ось стрелки тем точнее совпадает с этим направлением, чем больше сила тока и чем слабее влияние магнитного поля Земли. Эрстед обнаружил, что направление поворота северного полюса (
N) стрелки под действием электрического тока изменяется на противоположное при изменении направления тока в проводнике.
Таким образом, при прохождении по проводнику электрического тока вокруг него возникает магнитное поле, действующее на помещенную в него магнитную стрелку.
Опыты показывают, что вокруг всякого движущегося заряда помимо электрического поля существует также и магнитно.
Электрическое поле действует как на неподвижные, так и на движущиеся заряды.
Важнейшая особенность магнитного поля состоит в том, что оно действует только на
движущиеся в этом поле электрические заряды. Характер воздействия магнитного поля на ток зависит от формы проводника, по которому течет ток, от расположения проводника в силовом поле и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный электрический ток.
Для обнаружения и исследования магнитного поля используется замкнутый плоский контур с током -
рамка с током, размеры которой малы по сравнению с расстоянием до токов, создающих магнитное поле. Ориентация контура в пространстве характеризуется направлением нормали к плоскости рамки. В качестве положительного направления нормали принимается направление, связанное стоком
правилом буравчика: за положительное направление нормали принимается направление поступательного движения винта, рукоятка которого вращается в направлении тока, текущего в рамке (рис. 3.2)
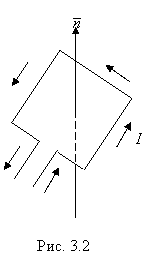
Если поместить рамку с током в магнитное поле, то поле будет оказывать на рамку ориентирующее воздействие, поворачивая ее соответствующим образом. Это связано с определенным направлением магнитного поля.
За направление магнитного поля принимается направление, вдоль которого располагается положительная нормаль к рамке. За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, действующей на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая
S-N, совпадала с направлением поля.
Рамкой с током можно воспользоваться и для
количественного описания магнитного поля. Так как рамка испытывает на себе ориентирующее действие поля, на нее в магнитном поле действует
пара сил. Вращающий момент сил зависит от
свойств магнитного поля в данной точке и от параметров самой рамки:
(3.1)
где
вектор индукции магнитного поля, являющийся силовой характеристикой поля; вектор магнитного момента рамки с током. Для плоской рамки, по которой протекает ток силой
I,
где
S – площадь поверхности контура; единичный вектор нормали к поверхности рамки. Направление совпадает, таким образом, с направлением положительной нормали. Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них будут действовать различные по величине вращающие моменты, однако отношение для всех контуров будет одним и тем же и поэтому может служить
количественной характеристикой магнитного поля, называемой
магнитной индукцией: (3.2)
Таким образом, магнитная индукция в данной точке
однородного поля определяется максимальным
вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна к направлению поля (аналог ).
Так как
магнитное поле является силовым, его, по аналогии с электрическим полем, изображают с помощью
линий магнитной индукции - линий, касательные к которым в каждой точке совпадают с направлением вектора . Их направление определяется правилом буравчика: рукоятка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.
Линии магнитной индукции всегда замкнуты и охватывают проводники с токами или постоянные магниты. Этим они отличаются от линий напряженности электростатического поля, которые являются разомкнутыми (начинаются на положительных зарядах, обрываются на отрицательных и вблизи поверхности заряженного тела направлены перпендикулярно к ней).
Согласно предположению Ампера, в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Эти токи создают свое магнитное поле и могут поворачиваться в магнитных полях макроскопических токов (токов, текущих в проводниках). Так, если вблизи какого-то тела (среды) поместить проводник с током, т.е. макроток, то под действием его магнитного поля микротоки в атомах тела определенным образом ориентируются, создавая тем самым дополнительное магнитное поле. Поэтому вектор магнитной индукции характеризует
результирующее магнитное поле, создаваемое всеми макро- и микротоками, т.е. при одном и том же токе
I и прочих равных условиях вектор в различных средах будет иметь разные значения.
Магнитное поле, создаваемое макротоками, характеризуется вектором напряженности . Для однородной изотропной среды связь между векторами индукции и напряженности магнитного поля определяется выражением
(3.3) где
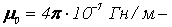
магнитная постоянная, магнитная проницаемость среды (безразмерная величина), показывающая, во сколько раз магнитное поле макротоков усиливается за счет поля микротоков данной среды. Единица напряженности магнитного поля –
ампер на метр:
1 А/м - напряженность такого поля, магнитная индукция которого в вакууме равна
4π·10-7 Тл.
ЗАКОН БИО-САВАРА В отличие от электpического поля магнитное поле не только воздействует лишь на движущиеся заpяды, но и создается лишь движущимися заpядами. Обычно движущиеся заpяды пpедставлены токами. Поэтому и pассмотpим постоянный ток, идущий по очень тонкому пpоводу. Пpовод наполнен движущимся со скоpостью v заpядом. Выбеpем малый участок пpовода dl и заpяд, его заполняющий, обозначим чеpез dq. Нас будет интеpесовать м
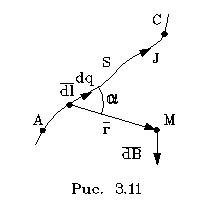
агнитное поле от заpяда dq в пpоизвольной точке пpостpанства М. Вспомним закон Кулона. Напpяженность электpического поля, создаваемого заpядом dq, обpатно пpопоp-циональна квадpату pасстояния от заpяда до данной точки поля: dE dq/r2. Закон Био-Саваpа-Лапласа фоpмулиpуется аналогичным обpазом.
Индукция магнитного поля пpямо пpопоpциональна заpяду и обpатно пpопоpциональна квадpату pасстояния от заpяда. Однако магнитное поле еще зависит и от скоpости движения заpяда: индукция магнитного поля пpопоpциональна скоpости движения заpяда и синусу угла между напpавлениями скоpости и pадиуса-вектоpа, пpоведенного от заpяда в данную точку поля. В виде фоpмулы закон Био-Саваpа-Лапласа записывается следующим обpазом:
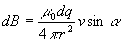
(3.18)Напpавление индукции поля dB опpеделяется пpавилом пpавого винта: dB напpавлен пеpпендикуляpно к элементу пpоводника d и к pадиусу-вектоpу точки r, в котоpой опpеделяются паpаметpы поля, его напpавление совпадает с вpащательным движением пpавого винта, если его повоpачивать от элемента тока к pадиусу-вектоpу.
Пpоизведение dqv можно пpеобpазовать следующим обpазом:
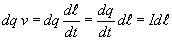
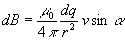
Следовательно, фоpмула закона Био-Саваpа-Лапласа пpинимает вид(3.19)Однако фоpмула (
3.19) опpеделяет лишь поле от элемента тока d . Чтобы иметь возможность найти pезультиpующее магнитное поле от тока и
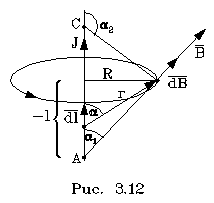
ли магнитное поле от участка конечной длины, нужно воспользоваться пpинципом супеpпозиции, котоpый для магнитного поля выполняется так же,как и для электpического. Следовательно, если нас интеpесует магнитное поле от конечного участка тока (напpимеp, от участка АС на
pис. 3.11), то следует взять кpиволинейный вектоpный интегpал такого вида:
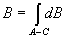
(3.20)
Рассмотpим магнитное поле от тонкого пpямолинейного пpовода с током. Элементаpные поля от pазличных элементов тока в данном случае напpавлены по одной пpямой (
pис. 3.12), и вектоpное интегpиpование сводится к алгебpаическому интегpиpованию.
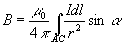
(3.21)
Чтобы вычислить интегpал, в подынтегpальном выpажении все пеpеменные должны быть выpажены чеpез какую-то одну пеpеменную. В качестве такой пеpеменной пpимем угол . Запишем очевидные соотношения:
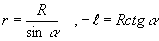
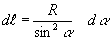
Их подстановка в фоpмулу (
3.21) пpиводит к выpажению:
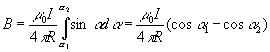
(3.22)
Если пpямой пpовод бесконечно длинный ,то
1 = 0,
2 = , и поле описывается такой фоpмулой:
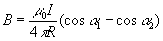
(3.23)
Очевидно, что магнитное поле в данном случае обладает цилиндpической симметpией, и его силовые линии пpедставляют собой концентpические окpужности, центpы котоpых лежат на пpоводнике с током.
Тот факт, что силовые линии магнитного поля замкнуты, является общим для любого магнитного поля.
Этим магнитное поле pадикально отличается от электростатического, силовые линии котоpого всегда pазомкнуты: они начинаются на положительных и заканчиваются на отpицательных заpядах. Если на электpические заpяды смотpеть как на источники электpического поля, то можно сказать, что магнитных заpядов в пpиpоде нет.
МАГНТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЗАРЯДА.СИЛА ЛОРЕНЦА
Любой проводник с током создает в окружающем пространстве магнитное поле. В свою очередь ток представляет собой упорядоченное движение электрических зарядов. Отсюда следует, что каждый движущийся в вакууме или среде заряд создает вокруг себя магнитное поле.

Опытно установлен закон, определяющий магнитное поле индукцией точечного заряда
q, свободно движущегося с нерелятивистской скоростью :
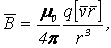
(3.11)
где - радиус-вектор, проведенный от заряда
q к данной точке поля. Вектор направлен перпендикулярно к плоскости, проведенной через векторы и , а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от к (рис. 3.6).
Модуль вектора магнитной индукции определяется выражением
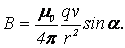
(3.12) Сравнивая (3.11) с выражением (3.5), можно сделать вывод, что движущийся заряд по своим магнитным свойствам соответствует элементу тока:
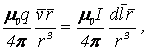
или Приведенные закономерности справедливы лишь при относительно малых скоростях движущихся зарядов. т.е. когда электрическое поле свободно движущегося заряда можно считать электростатическим. Сила, действующая со стороны магнитного поля на движущийся в нем электрический заряд, называется
силой Лоренца: (3.13)

Направление силы Лоренца определяется
правилом левой руки: если ладонь левой руки расположить так, чтобы в нее входили линии индукции магнитного поля, а четыре вытянутых пальца направить вдоль вектора , то отогнутый большой палец покажет направление силы, действующей на
положительный заряд (рис. 3.7). На отрицательный заряд сила со стороны магнитного поля действует в противоположном направлении.
Модуль силы Лоренца определяется по формуле где - угол между векторами и .
Сила Лоренца всегда перпендикулярна вектору движения заряженной частицы, поэтому она не изменяет модуля ее скорости. Это означает, что постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией действует и электрическое поле напряженностью , то результирующая сила , приложенная к заряду, равна векторной сумме двух составляющих – электрической и магнитной (
формула Лоренца):
Разделение силы Лоренца на электрическую и магнитную составляющие относительно, так как они зависят от выбора инерциальной системы отсчета. Это объясняется тем, что при переходе от одной инерциальной системы отсчета к другой изменяются не только скорость заряда, но и силовые характеристики и полей. Соответственно разделение электромагнитного поля на электрическое и магнитное поля тоже относительно.
МАГНИТНОЕ ПОЛЕ КРУГОВОГО ТОКА Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R (рис. 1.7).
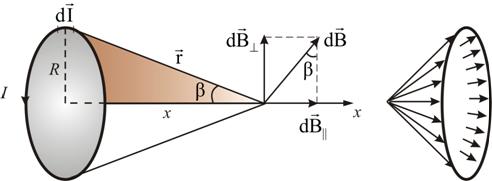
Рис. 1.7
Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы перпендикулярны плоскостям, проходящим через соответствующие и . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор направлен вдоль оси кругового тока. Каждый из векторов вносит вклад равный , а взаимно уничтожаются. Но , , а т.к. угол между и α – прямой, то тогда получим, (1.6.1)
Подставив в (1.6.1) и, проинтегрировав по всему контуру , получим выражение для нахождения магнитной индукции кругового тока: 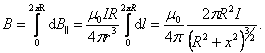 ,(1.6.2)При , получим магнитную индукцию в центре кругового тока: , (1.6.3) Заметим, что в числителе (1.6.2) – магнитный момент контура. Тогда, на большом расстоянии от контура, при , магнитную индукцию можно рассчитать по формуле: , (1.6.4) Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками (рис. 1.8). ,(1.6.2)При , получим магнитную индукцию в центре кругового тока: , (1.6.3) Заметим, что в числителе (1.6.2) – магнитный момент контура. Тогда, на большом расстоянии от контура, при , магнитную индукцию можно рассчитать по формуле: , (1.6.4) Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками (рис. 1.8).
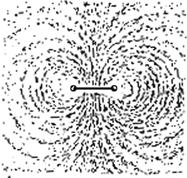
Рис. 1.8
|
ПРОВОДНИК С ТОКОМ В МАГНИТНОМ ПОЛЕ.ЗАКОН АМПЕРА
Обобщая результаты действия магнитного поля на различные проводники с током, А. Ампер установил, что сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока
I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :
(3.14). Направление силы определяется правилом левой руки. Модуль силы Ампера находится по формуле (3.15)
где - угол между векторами и .
Из формулы (3.15) следует, что сила максимальна, если элемент проводника с током расположен перпендикулярно линиям магнитной индукции: Из последнего выражения можно получить формулу для численного определения магнитной индукции:
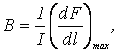
Единица магнитной индукции –
тесла (Тл): 1 Тл = 1 Н /(А·м).
Закон Ампера применяется для определения силы взаимодействия токов. Рассмотрим два протяженных параллельных проводника с токами и расстояние между которыми
R (рис. 3.8). Каждый из проводников создает магнитное поле, которое действует по закону
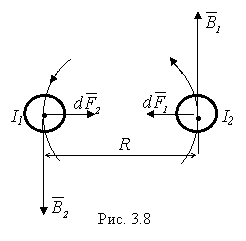
Ампера на другой проводник с током. Определим силу, с которой действует магнитное поле тока на элемент второго проводника с током.
Ток создает вокруг себя магнитное поле, линии индукции которого представляют собой концентрические окружности. Направление вектора определяется правилом буравчика, а модуль находится по формуле
Направление силы , с которой поле действует на участок второго проводника с током, определяется по правилу левой руки и указано на рисунке. Модуль этой силы с учетом того, что угол между элементом тока и вектором прямой, равен
Подставляя сюда значение , получим:
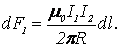
(3.16)
Рассуждая аналогично, можно определить силу , с которой магнитное поле тока действует на элемент первого проводника с током . Эта сила направлена в противоположную сторону и по модулю равна

(3.17)
Сравнение (3.16) и (3.17) показывает, что , т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой
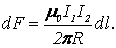
(3.18)
Если токи в проводниках имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (3.18).
Релятивистская трактовка магнитных явлений Релятивистское уравнение движения имеет одинаковый вид во всех инерциальных системах отсчёта: ,(7.6.1)Требования релятивистской инвариантности уравнения движения приводит к тому, что силы оказываются связанными определенными соотношениями при переходе от одной системы к другой. Причём из формулы преобразования сил следует неизбежная зависимость силы от скорости в релятивистской теории. Существование магнитной и электрической сил можно выявить из следующего примера взаимодействия зарядов. Имеем штрихованную систему отсчёта , движущуюся со скоростью относительно неподвижной системы отсчёта K. Причём движется в направлении увеличения x (рис. 7.4).
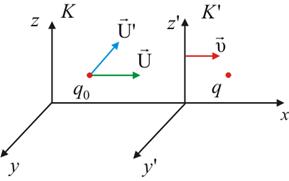
Рис. 7.4Заряд q неподвижен в системе , – движется в K со скоростью U, а в со скоростью U'. Рассмотрим взаимодействие этих двух зарядов в системе K и . Для этого нам необходимо знать закон преобразования сил при переходе от одной инерциальной системы отчёта к другой и влияние перехода на величину заряда. Однако величина заряда не зависит от выбора системы отсчёта. Если бы это было не так, то многоэлектронный атом, в котором электроны движутся с разными скоростями, не был бы электрически нейтральным.
Сначала рассмотрим взаимодействие зарядов в системе : q – неподвижен, – движется. Таким образом, сила, с которой q действует на – кулоновская. Она будет зависеть от координат q и не зависеть от скорости : эта сила определяется электростатическим полем, которое создаёт заряд q. Тогдаи , где – сила электростатическоговзаимодействия.Теперь рассмотрим взаимодействие этих же зарядов в системе K. Найдём силу, которая действует на заряд q в этой системе.Согласно формулам преобразования сил при переходе из одной системы отсчёта в другую, ,(7.6.2)где 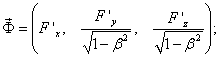 . Можно записать: или . Умножим и разделим правую часть на q0:. Если , , то получим классический случай, т.е. – напряжённость электрического поля, создаваемого зарядом q в системе К.Тогда – это электрическая сила, действующая на заряд q0 в системе K, она не зависит от скорости частицы U. Рассмотрим второе слагаемое. – это слагаемое определяет зависимость силы от скорости заряда . К тому же, если , то . . Можно записать: или . Умножим и разделим правую часть на q0:. Если , , то получим классический случай, т.е. – напряжённость электрического поля, создаваемого зарядом q в системе К.Тогда – это электрическая сила, действующая на заряд q0 в системе K, она не зависит от скорости частицы U. Рассмотрим второе слагаемое. – это слагаемое определяет зависимость силы от скорости заряда . К тому же, если , то .
Таким образом,кроме кулоновской силы , на заряд действует другая сила.. Она возникает в результате движения зарядов и называется магнитной. То есть движение зарядов создаёт в пространстве магнитное поле, или на движущийся заряд со стороны магнитного поля действует сила . –индукция магнитного поля:
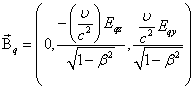 . Из сравнения и видно, что, при , является величиной второго порядка малости относительно – силы кулоновского взаимодействия. Следовательно, магнитное взаимодействие сравнимо с электрическим по величине лишь при достаточно больших скоростях ( ) заряженных частиц. Таким образом, при , при .Полную силу, действующую на заряд со стороны заряда q в системе K, можно записать как: Таким образом, магнитное поле мы ввели, исходя из инвариантности заряда и релятивистского закона преобразования сил. Рассмотренное нами поле заряда q может быть и чисто электрическим, и одновременно электрическим и магнитным, в зависимости от того, в какой системе отсчёта мы его наблюдаем. Это обстоятельно подчеркивает единство электромагнитного поля, а проведённые нами выкладки свидетельствуют, что основным законом электричества и магнетизма является закон Кулона. Все остальные законы магнитостатики могут быть получены из закона Кулона, инвариантности заряда и релятивистского закона преобразования сил (полей). . Из сравнения и видно, что, при , является величиной второго порядка малости относительно – силы кулоновского взаимодействия. Следовательно, магнитное взаимодействие сравнимо с электрическим по величине лишь при достаточно больших скоростях ( ) заряженных частиц. Таким образом, при , при .Полную силу, действующую на заряд со стороны заряда q в системе K, можно записать как: Таким образом, магнитное поле мы ввели, исходя из инвариантности заряда и релятивистского закона преобразования сил. Рассмотренное нами поле заряда q может быть и чисто электрическим, и одновременно электрическим и магнитным, в зависимости от того, в какой системе отсчёта мы его наблюдаем. Это обстоятельно подчеркивает единство электромагнитного поля, а проведённые нами выкладки свидетельствуют, что основным законом электричества и магнетизма является закон Кулона. Все остальные законы магнитостатики могут быть получены из закона Кулона, инвариантности заряда и релятивистского закона преобразования сил (полей).
|
 Скачать 1.44 Mb.
Скачать 1.44 Mb.

 Ампера на другой проводник с током. Определим силу, с которой действует магнитное поле тока на элемент второго проводника с током.
Ампера на другой проводник с током. Определим силу, с которой действует магнитное поле тока на элемент второго проводника с током. 
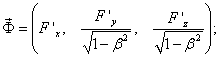 . Можно записать: или . Умножим и разделим правую часть на q0:. Если , , то получим классический случай, т.е. – напряжённость электрического поля, создаваемого зарядом q в системе К.Тогда – это электрическая сила, действующая на заряд q0 в системе K, она не зависит от скорости частицы U. Рассмотрим второе слагаемое. – это слагаемое определяет зависимость силы от скорости заряда . К тому же, если , то .
. Можно записать: или . Умножим и разделим правую часть на q0:. Если , , то получим классический случай, т.е. – напряжённость электрического поля, создаваемого зарядом q в системе К.Тогда – это электрическая сила, действующая на заряд q0 в системе K, она не зависит от скорости частицы U. Рассмотрим второе слагаемое. – это слагаемое определяет зависимость силы от скорости заряда . К тому же, если , то .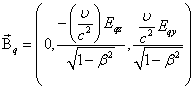 . Из сравнения и видно, что, при , является величиной второго порядка малости относительно – силы кулоновского взаимодействия. Следовательно, магнитное взаимодействие сравнимо с электрическим по величине лишь при достаточно больших скоростях ( ) заряженных частиц. Таким образом, при , при .Полную силу, действующую на заряд со стороны заряда q в системе K, можно записать как: Таким образом, магнитное поле мы ввели, исходя из инвариантности заряда и релятивистского закона преобразования сил. Рассмотренное нами поле заряда q может быть и чисто электрическим, и одновременно электрическим и магнитным, в зависимости от того, в какой системе отсчёта мы его наблюдаем. Это обстоятельно подчеркивает единство электромагнитного поля, а проведённые нами выкладки свидетельствуют, что основным законом электричества и магнетизма является закон Кулона. Все остальные законы магнитостатики могут быть получены из закона Кулона, инвариантности заряда и релятивистского закона преобразования сил (полей).
. Из сравнения и видно, что, при , является величиной второго порядка малости относительно – силы кулоновского взаимодействия. Следовательно, магнитное взаимодействие сравнимо с электрическим по величине лишь при достаточно больших скоростях ( ) заряженных частиц. Таким образом, при , при .Полную силу, действующую на заряд со стороны заряда q в системе K, можно записать как: Таким образом, магнитное поле мы ввели, исходя из инвариантности заряда и релятивистского закона преобразования сил. Рассмотренное нами поле заряда q может быть и чисто электрическим, и одновременно электрическим и магнитным, в зависимости от того, в какой системе отсчёта мы его наблюдаем. Это обстоятельно подчеркивает единство электромагнитного поля, а проведённые нами выкладки свидетельствуют, что основным законом электричества и магнетизма является закон Кулона. Все остальные законы магнитостатики могут быть получены из закона Кулона, инвариантности заряда и релятивистского закона преобразования сил (полей).
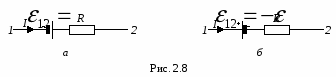
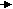 этой формуле ЭДС
этой формуле ЭДС  юбая точка разветвленной электрической цепи, в которой сходится не менее трех проводников тока, называется узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла – отрицательным (рис. 2.9).
юбая точка разветвленной электрической цепи, в которой сходится не менее трех проводников тока, называется узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла – отрицательным (рис. 2.9).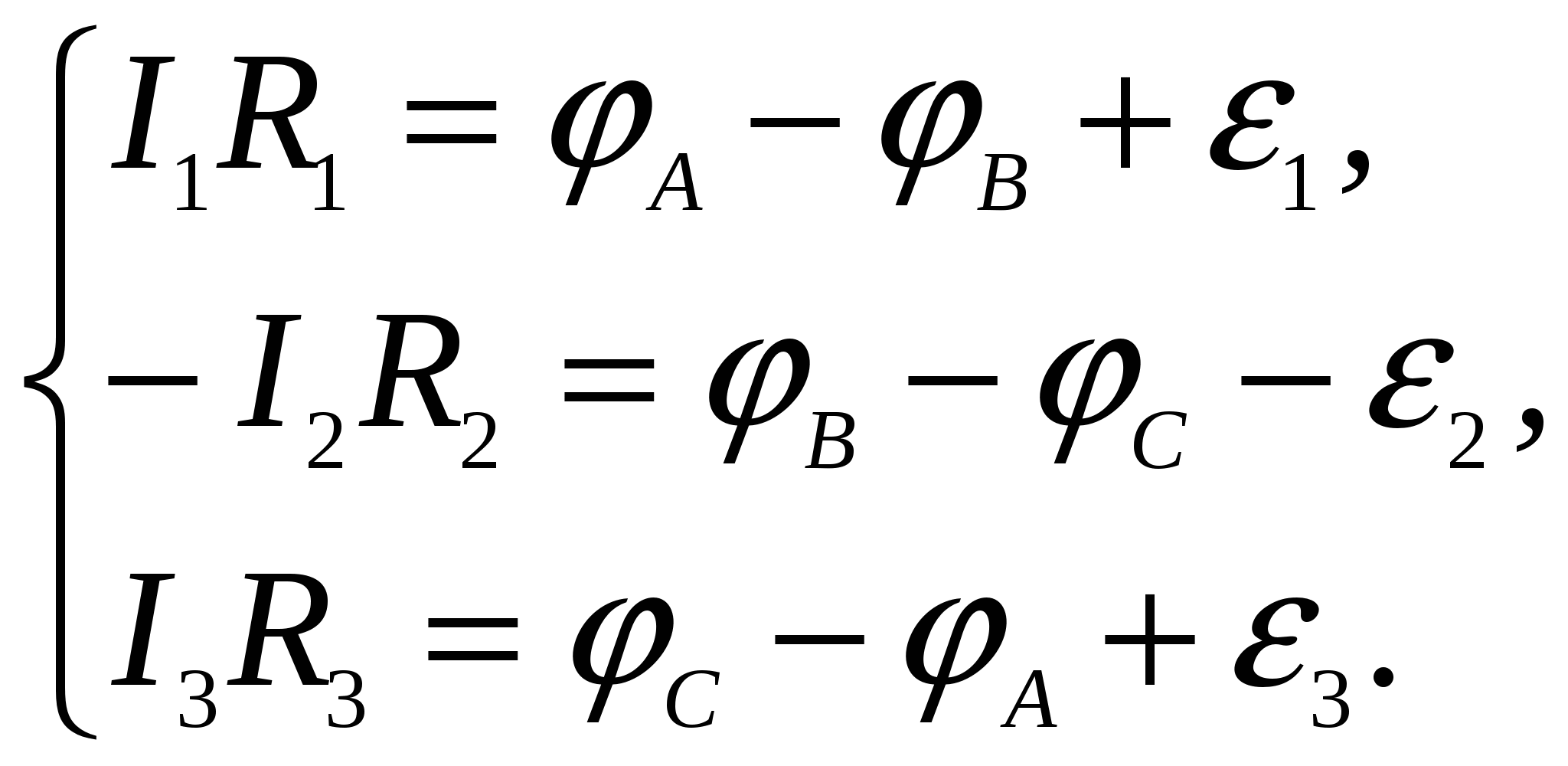 Складывая почленно эти уравнения, получим:
Складывая почленно эти уравнения, получим: где n – количество источников тока в контуре; m – число участков в контуре.
где n – количество источников тока в контуре; m – число участков в контуре.

 агнитное поле от заpяда dq в пpоизвольной точке пpостpанства М. Вспомним закон Кулона. Напpяженность электpического поля, создаваемого заpядом dq, обpатно пpопоp-циональна квадpату pасстояния от заpяда до данной точки поля: dE dq/r2. Закон Био-Саваpа-Лапласа фоpмулиpуется аналогичным обpазом.
агнитное поле от заpяда dq в пpоизвольной точке пpостpанства М. Вспомним закон Кулона. Напpяженность электpического поля, создаваемого заpядом dq, обpатно пpопоp-циональна квадpату pасстояния от заpяда до данной точки поля: dE dq/r2. Закон Био-Саваpа-Лапласа фоpмулиpуется аналогичным обpазом. ли магнитное поле от участка конечной длины, нужно воспользоваться пpинципом супеpпозиции, котоpый для магнитного поля выполняется так же,как и для электpического. Следовательно, если нас интеpесует магнитное поле от конечного участка тока (напpимеp, от участка АС на
ли магнитное поле от участка конечной длины, нужно воспользоваться пpинципом супеpпозиции, котоpый для магнитного поля выполняется так же,как и для электpического. Следовательно, если нас интеpесует магнитное поле от конечного участка тока (напpимеp, от участка АС на 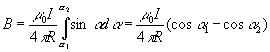 (3.22)
(3.22) Опытно установлен закон, определяющий магнитное поле индукцией точечного заряда q, свободно движущегося с нерелятивистской скоростью :
Опытно установлен закон, определяющий магнитное поле индукцией точечного заряда q, свободно движущегося с нерелятивистской скоростью : 