Ответы на вопросы в экзаменационных билетах. Физика. 2 курс. Электрический ток и его характерстики
 Скачать 1.44 Mb.
|
Магнитное поле в веществе. Намагниченность. Напряженность магнитного поляГипотеза Ампера: магнитные свойства вещества обусловлены элементарными замкнутыми токами, циркулирующими внутри небольших частиц вещества – атомов, молекул или их групп. При описании магнитного поля в веществе – магнетике можно, не вдаваясь в природу этих элементарных токов, считать их все одинаковыми. Пусть каждая молекула вещества характеризуется некоторым магнитным моментом  , (4.4.1)где Iмол элементарный молекулярный ток, а Sмол – площадь, охваченная его контуром. Количественной характеристикой намагниченного состояния вещества служит векторная величина намагниченность J, равная отношению магнитного момента Pm макроскопически малого объёма DV вещества к этому объему:
 , (4.4.2)где pmi – магнитный момент i- молекулы из общего числа N молекул, содержащихся в объеме DV. Этот объем должен быть столь малым, чтобы в его пределах магнитное поле можно было считать однородным. В то же время в нем должно содержаться столь большое число молекул (N>>1), чтобы к ним можно было применять статистические методы. Если магнетик не намагничен, молекулярные токи ориентированы хаотически и средняя намагниченность равна нулю. Под действием магнитного поля В0, создаваемого внешними токами, происходят различные процессы намагничивания вещества при этом возникает дополнительное усредненное магнитное поле В1 молекулярных токов, так что суммарное поле В, действующее в магнетике, характеризуется магнитной индукцией В 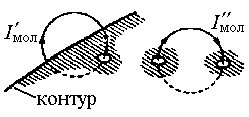 = В0 + В1. (4.4.3)Закон полного тока для магнитного поля в веществе имеет вид  ,(4.4.4)г де Iмакро и Iмикро – алгебраические суммы соответственно макро- и микротоков, проходящих через замкнутый контур L , т.е. результирующие макро- и микротоки пересекающие поверхность, натянутую на этот контур. Н 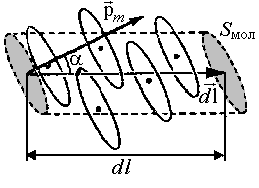 айдем связь между Iмикро и намагниченностью вещества. Вклад в этот ток дают только те молекулярные токи I’мол (см рис. 4.4.1.), которые «нанизаны» на контур L как бусы на нитку. Будем полагать, что магнитные моменты всех молекулярных токов pmiориентированы одинаково. Пусть a угол между вектором dl малого элемента замкнутого контура L и векторами pmi . На элемент контура dl «нанизаны» молекулярные токи dn молекул, находящихся в объеме косого цилиндра (рис. 4.4.2.) с образующей dl и основанием, равным Sмол ,нормаль к которой составляет угол a с образующей цилиндра:  , (4.4.5.)где n концентрация молекулярных токов.Таким образом, малому элементу dl контура L соответствует охватываемый этим контуром микроток, который с учетом (4.4.1) можно записать в виде  . (4.4.6)Интегрируя это выражение по всему замкнутому контуру L, находим полный микроток  , (4.4.7)следовательно, микроток Iмикро , охваченный замкнутым контуром L равен циркуляции намагниченности J по этому контуру. С учетом выражения (4.4.7) закон полного тока (4.4.4) можно преобразовать к следующему виду:  .(4.4.8)НАПРЯЖЁННОСТЬ Вектор H=B/m0 - J (4.4.9) называется напряженностью магнитного поля(магнитной напряженностью). Используя напряженность магнитного поля H, закон полного тока для магнитного поля в веществе можно записать в виде  (4.4.10)Таким образом, циркуляция напряженности магнитного поля вдоль произвольного контура равна результирующему макротоку сквозь поверхность, натянутую на этот контур.В случае многих однородных изотропных веществ,между намагниченностью и магнитной индукцией есть прямая пропорциональность:  . (4.4.11)С учетом этого из формулы (4.4.9) находим, что напряженность магнитного поля также пропорциональна магнитной индукции. Соотношение между этими величинами принято записывать в виде  . (4.4.12)Входящая в коэффициент пропорциональности константа m называется относительной магнитной проницаемостью вещества. Подставив преобразованное соотношение (4.4.12)  (4.4.13)в (4.4.9), получим . (4.4.14)Величина c называется магнитной восприимчивостью вещества и связана с магнитной проницаемостью соотношением  . (4.4.15) |