Ответы на вопросы в экзаменационных билетах. Физика. 2 курс. Электрический ток и его характерстики
 Скачать 1.44 Mb.
|
Дивергенция и ротор магнитного поля.М
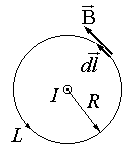 агнитная индукция бесконечно длинного прямого повода с током находится по формуле  . Проведем через точку наблюдения, отстоящую от проводя на произвольное расстояние R окружность Lконцентричную проводу (см рис.3.6.1). На всей этой окружности значение неизменно, а сам вектор B направлен по касательной к окружности (Bl= B). Поэтому циркуляция вектора B по окружности вычисляется так:  .( ), (3.7.1)К
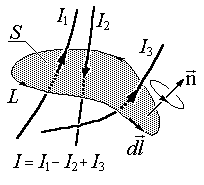ак видим, циркуляция B не зависит от радиуса окружности, а определяется только током, охваченным ею. Можно показать, что это свойство магнитного поля остается справедливым и для случая произвольного по форме контура интегрирования L, а также в том случае, когда через площадь S(см. рис.3.7.2), охваченную контуром протекают несколько токов, т.е.  . (3.7.2)При этом под I подразумевается алгебраическая сумма этих токов. Знак плюс в этой сумме соответствует токам, направление которых связано с выбором направления вектора  в левой части (3.7.2) правилом правого винта. Токи противоположного направления входят в суммарный ток, обозначенный в формуле (3.7.2) через I , со знаком минус (см. ток I2 на рис.3.7.2). Применим закон полного тока для бесконечно малой окружности площадью dS, через которую протекает бесконечно малый ток dI. Используя формулу, выражающую ток через площадку через плотность тока, т.е. dI =j dS, получим закон полного тока в дифференциальной форме:  . (3.7.3)Формула (3.7.3) указывает на то, что ротор магнитного поля не равен тождественно нулю, как для электростатического поля. Поэтому вектор магнитной индукции в области, где протекают токи, не является градиентом никакой скалярной функции .В области, где протекают токи, ротор магнитного поля отличен от нуля. Это означает, что изображение магнитного поля магнитными силовыми линиями в этой области невозможно (силовая линия не может проходить через точку, где ротор не равен нулю, а как бы полностью стягивается в эту точку), не может быть введен и потенциал магнитного поля, т.к. в области, где протекают токи, не существует скалярной функции такой, что  равно ее градиенту. Это свидетельствует о непотенциальности магнитного поля. Сравним дифференциальные уравнения для магнитного поля с дифференциальными уравнениями, описывающими электростатическое поле (в пустоте):  ,  ; , . (3.7.4)Дивергенция электростатического поля не равна нулю в области источников. Силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных. Дивергенция магнитного поля везде равна нулю. Магнитные силовые линии вне источников магнитного поля замкнуты (в области источников поля вообще не имеют смысла). Ротор электростатического поля, как и его циркуляция, тождественно равен нулю. В любой точке вектор напряженности электростатического поля выражается через градиент некоторой скалярной функции, называемой потенциалом. Электростатическое поле потенциально. Ротор В не равен нулю в области источников. Из-за этого и циркуляция В не равна нулю в этой области. Вектор В не является градиентом никакой скалярной функции координат. Магнитное поле, таким образом, непотенциально (является вихревым).. Итак, электрические токи (направленное движение заряда) создают магнитное поле, а нескомпенсированные заряды – электростатическое поле. Внутри проводника имеется электрическое поле из-за наличия ЭДС в цепи с током. Вокруг проводника имеется магнитное поле, которое находится с помощью закона Био-Савара-Лапласа МАГНИТНОЕ ПОЛЕ СОЛЕНОИДАПусть соленоид длиной l, во много раз превышающей его диаметр, имеет N витков, по которым течет ток силой I. Если соленоид находится в вакууме (или воздухе), то магнитная индукция поля в нем численно равнаB0 = μ0 IN / l = μ0 In,где n = N/l; In – число ампер-витков, приходящихся на единицу длины соленоида; μ0 – магнитная постоянная, характеризующая магнитное поле в вакууме.Поле внутри длинного соленоида однородно и направлено от южного полюса (S) к северному (N). Модуль магнитной индукции поля в соленоиде пропорционален числу ампервитков, приходящихся на единицу его длины. |