Ответы на вопросы в экзаменационных билетах. Физика. 2 курс. Электрический ток и его характерстики

• Название: Электрический ток и его характерстики
• Анкор: Ответы на вопросы в экзаменационных билетах. Физика. 2 курс.doc
• Дата: 27.12.2017
• Размер: 1.44 Mb.
• Имя файла: Ответы на вопросы в экзаменационных билетах. Физика. 2 курс.doc
• Тип: Документы; #13164
• Категория: Физика
• страница: 2 из 7

СИЛА И МОМЕНТСИЛ,ДЕЙСТВУЮЩИЕНА КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ.

Рассмотрим замкнутый плоский проводник с током (контур с током). Выберем вектор n, перпендикулярный плоскости контура и согласованный с направлением тока по правилу правого винта. Пусть сила тока в контуре I и площадь, охваченная контуром S. Вектор , (4.3.1)определяет взаимодействие контура с магнитным полем. Этот вектор называется магнитным дипольным моментом контура с током..

Поместим этот контур в однородное магнитное поле с индукцией В, тогда на каждый элемент контура dl будет действовать сила .(4.3.2)Суммируя силы, приложенные к элементам контура, получим для результирующей силы. (4.3.3)

Здесь сила тока и магнитная индукция для всех элементов контура одинаковы, поэтому их можно вынести из-под знака интеграла. Интегрирование всех векторов dl, составляющих контур, дает вектор перемещения вдоль тока, который для замкнутого контура равен нулю, т. е. . Поэтому полная сила, действующая на замкнутый контур с током в однородном поле, тоже равна нулю:. (4.3.4)

Найдем далее момент сил (вращательный момент), действующий на контур с током в однородном магнитном поле. При этом учтем известный из механики факт, что если результирующая сил равна нулю, то момент сил не зависит от выбора точки, относительно которой он вычисляется.

Р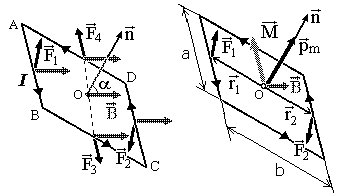ассмотрим прямоугольный контур ABCD, расположенный в однородном магнитном поле так, что вектор нормали n образует с вектором В угол a , и стороны AB и CD перпендикулярны вектору В.

Обозначим силы Ампера, действующие на стороны контура F₁,F₂,F₃,F₄ . Найдем суммарный момент этих сил относительно точки О (центра контура). Линии действия сил F₃,F₄ проходят через точку О, следовательно, моменты этих сил равны нулю. Две другие силы: F₁ и F₂ и радиус-векторы точек их приложения r₁ и r₂ лежат в плоскости, образованной векторами B и n . Расположение векторов в этой плоскости изображено на рисунке 4.3.2.

Каждая из сил F₁, F₂ перпендикулярна вектору В, а радиус-векторы r₁, r₂ перпендикулярны вектору n. Поэтому силы F₁, F₂ образуют с радиус-векторами r₁, r₂ тот же угол a, что и вектор B с нормалью n. Момент этих сил M равен . (4.3.5)

Слагаемые в этой сумме направлены в одну сторону (перпендикулярно плоскости рисунка от нас). По формуле (4.2.3) обе силы равны F₁=F₂=IaB, кроме того, r₁=r₂=b/2. Поэтому слагаемые в (4.3.5) одинаковы по величине и равны,(4.3.6)а величина результирующего момента

, (4.3.7)

где S= ab – площадь рамки. Воспользовавшись определением магнитного момента контура (4.3.1.), можно записать величину момента сил Ампера, действующих на этот контур: . (4.3.8)

Векторы p_m, B, M составляют правую тройку векторов, поэтому в общем виде получаем. (4.3.9)

Формула (4.3.9) справедлива в однородном магнитном поле для контура произвольной формы.

Как следует из формулы (4.3.8) для момента амперовых сил, существует два положения a = 0 и a = p, в которых этот момент обращается в нуль. В остальных случаях (см. рис.4.3.2) вращающий момент, действующий на контур с током, стремится развернуть контур так, чтобы направление магнитного момента контура совпало с направлением магнитной индукции внешнего поля, т.е. к состоянию a = 0. Поэтому при a = 0 контур оказывается в устойчивом равновесии, а при a = p – в неустойчивом.

Выше было доказано, что в однородном поле результирующая сила, действующая на контур, равна нулю. Можно показать, что на контур в неоднородном магнитном поле действует сила

. (4.3.10)

Здесь p_mx, p_my, p_mz проекции вектора магнитного момента на координатные оси x, y, z. Векторное уравнение (4.3.10) в проекции, например, на ось х означает, что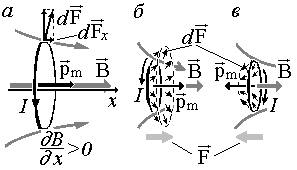

, (4.3.11)

г

Рис. 4.3.3

де B_x, B_y, B_z – проекции магнитной индукции на координатные оси. В частном случае, если вектор магнитной индукции изменяется только в том же направлении, в котором направлен вектор B, можно направить ось x по вектору B. Пусть кроме того величина вектора магнитной индукции возрастает в направлении оси x , т. е. . При этом знак проекции силы, действующей на контур, будет определяться знаком проекции p_mx. Иными словами, если угол между магнитным моментом контура и осью x острый (p_mx>0), то сила направлена в сторону оси, т.е. в сторону возрастания величины индукции. Если угол тупой (p_mx<0), то сила направлена в противоположную сторону. Рисунок 4.3.3 иллюстрирует, почему это происходит. На каждый элемент провода действует сила dF, проекция dF_x которой (рис. 4.3.3a) для всех элементов направлена в одну сторону и складывается в общую силу. Если магнитный момент направлен параллельно магнитной индукции (рис. 4.3.3б, ), результирующая сила F направлена в сторону возрастания модуля магнитной индукции. Если же магнитный момент направлен антипараллельно (рис. 4.3.3в, ), сила направлена в сторону убывания модуля B.

В общем случае под действием силы F незакрепленный контур с током втягивается в область более сильного магнитного поля, если угол a между векторами p_m и B острый. Если же угол a тупой, то контур с током выталкивается в область более слабого поля, поворачивается под действием момента сил Ампера, так, что угол a становится острым, и затем втягивается в область более сильного поля.

РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле , перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор  сонаправлен с .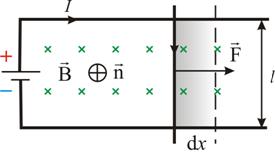Рис. 2.17

На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: Пусть проводник l переместится параллельно самому себе на расстояние  dx. При этом совершится работа:Итак, , Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток , пронизывающий контур, направлен по нормали  к контуру, поэтому .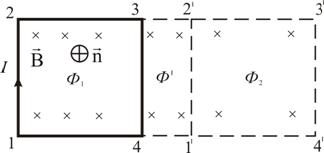



Рис. 2.18Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и  новый контур будет пронизан магнитным потоком .Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком .Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:где , равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).Провод1–2перерезает поток ( ), но движется против сил действия магнитного поля..Тогда общая работа по перемещению контура или,здесь  – это изменение магнитного потока, сцепленного с контуром.Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока,сцепленного с этим контуром.Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле,Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины dФ различен.Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется , то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу