Ответы на вопросы в экзаменационных билетах. Физика. 2 курс. Электрический ток и его характерстики
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
Уравнения Максвелла
Приведенные выше уравнения Максвелла не составляют еще полной системы уравнений электромагнитного поля, поскольку они не содержат свойства среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины , , , и , в которых учитываются индивидуальные свойства среды называются материальными уравнениями. Введённые обозначения:— плотность стороннего электрического заряда (в единицах СИ — Кл/м³) — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²) — напряжённость электрического поля (в единицах СИ — В/м) — напряжённость магнитного поля (в единицах СИ — А/м) — электрическая индукция (в единицах СИ — Кл/м²) — магнитная индукция (в единицах СИ — Тл = Вб/м²= кг·с-2·А-1) — сторонний электрический заряд, заключенный внутри поверхности (в единицах СИ — Кл) — электрический ток, проходящий через поверхность вызванный движением свободных зарядов (в единицах СИ — А) — замкнутая двумерная поверхность — замкнутый контур Материальные уравнения Чтобы дополнить уравнения Максвелла до полной системы уравнений электродинамики, необходимо получить материальные уравнения, которые связывают величины , , , , и в которых учтены индивидуальные свойства среды:,,где — диэлектрическая проницаемость (в единицах СИ — Ф/м), — магнитная проницаемость (в единицах СИ — Гн/м) и — электропроводность среды (в единицах СИ — 1/(Ом·м)). ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ОДНОРОДНОМ МАГИТНОМ ПОЛЕРассмотрим частный случай, когда нет электрического поля, но имеется магнитное поле. Предположим, что частица, обладающая начальной скоростью u0, попадает в магнитное поле с индукцией B. Это поле мы будем считать однородным и направленным перпендикулярно к скорости u0. 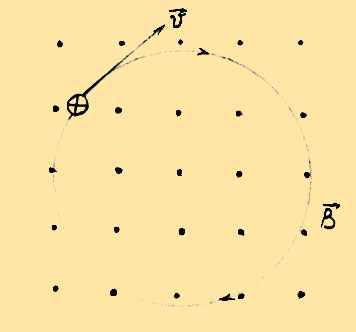 Основные особенности движения в этом случае можно выяснить, не прибегал к полному решению уравнений движения.Действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит, что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы не изменяется, то величина силы Лоренца Подставляя сюда вместо r его выражение по формуле (3.6), имеем: 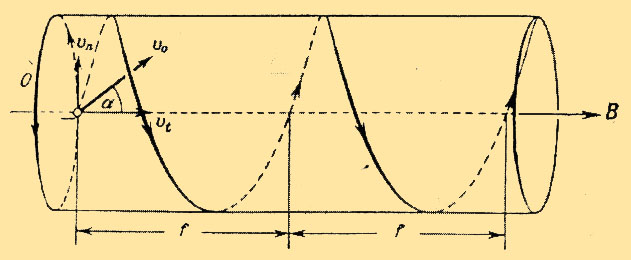 астицы составляет некоторый угол с направлением поля. В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Ut, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью астицы составляет некоторый угол с направлением поля. В этом случае удобно разложить скорость на две составляющие, одна из которых параллельна полю, а другая перпендикулярна к полю. На частицу действует сила Лоренца, и частица движется по окружности, лежащей в плоскости, перпендикулярной к полю. Составляющая Ut, не вызывает появления добавочной силы, так как сила Лоренца при движении параллельно полю равна нулю. Поэтому в направлении поля частица движется по инерции равномерно, со скоростью ДВИЖЕНИЕ ЗАР.ЧАСТИЦ В ОДНОРОДНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕЕсли частица, обладающая зарядом е, движется в пространстве, где имеется электрическое поле с напряжённостью E то на неё действует сила eE. Если, кроме электрического, имеется магнитное поле, то на частицу действует ещё сила Лоренца, равная e[uB] , где u - скорость движения частицы относительно поля, B - магнитная индукция. Поэтому согласно второму закону Ньютона уравнение движения частиц имеет вид: 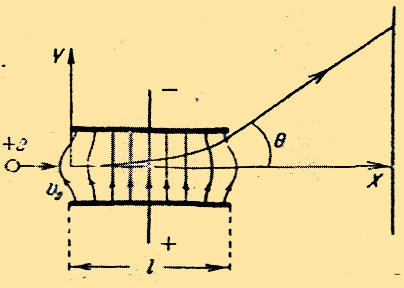 Если зазор между пластинами мал по сравнению с их длиной, то краевыми эффектами можно пренебречь и считать электрическое поле между пластинами однородным. Направляя ось Y параллельно полю, мы имеем: Отсюда получаем для угла отклонения: ЭФФЕКТ ХОЛЛА — явление возникновения поперечной разности потенциалов (называемой также Холловским напряжением) при помещении проводника с постоянным током в магнитное полеВ простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле B течет электрический ток под действием напряженности E. Магнитное поле будет отклонять носители заряда (для определенности электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости будет служить условие, что при этом электрон не начнет двигаться по спирали.Таким образом, сила Лоренца приведет к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1 не скомпенсирует магнитную составляющую силы Лоренца: Коэффициент пропорциональности между E1 и jB называется коэффициентом (константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (в сильных полях), таких как алюминий, цинк, железо, кобальт, наблюдается положительный знак RH, что объясняется в полуклассической и квантовой теориях твердого тела. На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля. |
