Ответы на вопросы в экзаменационных билетах. Физика. 2 курс. Электрический ток и его характерстики
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
|
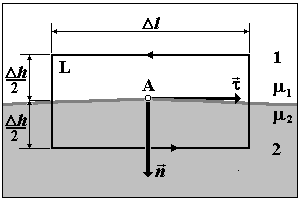
| Рис.4.6.1 |
айдем соотношение между магнитной индукцией B и напряженностью H магнитного поля в некоторой точке А на границе двух сред (см. рис 4.6.1). Проведем в точке А единичные векторы: t – по касательной вдоль границы раздела сред и n – по нормали к границе, направленной от первой среды ко второй. Построим вблизи точки А небольшой замкнутый прямоугольный контур L, две стороны которого параллельны вектору t и равны Dl, а две - вектору n и равны Dh. Предположим, что по границе раздела внутри контура вблизи точки А не текут макротоки. Из теоремы о циркуляции вектора напряженности магнитного поля следует, что
Здесь H1t и H2t - проекции напряженности H на направление касательного орта в точке А. Поскольку последнее равенство в (4.6.2) должно выполняться при произвольном Dl, находим
Таким образом, касательная к поверхности раздела двух сред составляющая напряженности магнитного поля не изменяется при переходе из одной среды в другую.
В
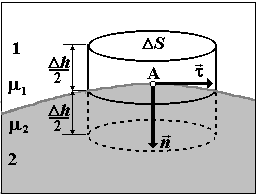
Рис.4.6.2
торое условие получим с помощью теоремы Гаусса для магнитной индукции B. Возьмем охватывающую окрестность точки А небольшую цилиндрическую поверхность S, основания DS которой параллельны границе раздела и лежат по разные стороны от нее (см. рис 4.6.2), а образующая параллельна вектору нормали n. По теореме Остроградского-Гаусса имеем для потока В через всю поверхность S
Поскольку это соотношение должно выполняться при любой площади основания DS, отличной от нуля, получаем
т.е. при переходе через границу раздела двух сред, нормальная составляющая вектора магнитной индукции не изменяется.
Из граничных условий (4.6.3) и (4.6.6) можно сделать следующие выводы: если граница раздела ортогональна линиям магнитной индукции, то вектор магнитной индукции не изменяется при переходе через границу. если граница раздела касается линий магнитной индукции, то напряженность магнитного поля не изменяется при переходе через границу раздела сред. Если первая среда - вакуум, т. е. m1=1, то получаем
Таким образом, относительная магнитная проницаемость среды показывает, во сколько раз увеличивается касательная составляющая вектора магнитной индукции при переходе из вакуума в данную среду (нормальная - не меняется). В этом проявляется существенное отличие магнитных материалов от диэлектрических. Для последних диэлектрическая проницаемость показывает во сколько раз уменьшается нормальная компонента напряженности электрического поля при переходе из вакуума в диэлектрик (касательная – не меняется).
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
Явление электромагнитной индукции можно наблюдать, когда в магнитном поле, образовавшемся между полюсами постоянного магнита, перемещается замкнутый проводник. Если этот проводник находится в покое, то в нем никакого тока не будет. Но стоит только сдвинуть его с места и перемещать так, чтобы он пересекал силовые линии магнитного поля, как тотчас же в проводнике появится электродвижущая сила и, как следствие – индукционный ток. В данном случае индукционный ток возникает в проводнике за счет той механической энергии, которая затрачивается при перемещении проводника в магнитном поле. При этом механическая энергия преобразуется в энергию электрическую.
Фарадей установил, что в замкнутом проводящем контуре индукционный ток возникает лишь в тех случаях, когда он находится в переменном магнитном поле, независимо от того, каким способом достигается изменение во времени потока индукции магнитного поля. Он показал, что при изменении сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение тока указывает на наличие в цепи электродвижущей силы. Значение ЭДС электромагнитной индукции
где k – коэффициент пропорциональности.
Р
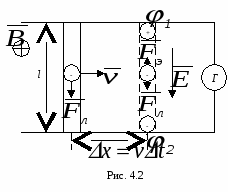 ассмотрим, как возникает ЭДС индукции, а, следовательно, индукционный ток. Пусть проводник без тока длиной l движется в магнитном поле с индукцией
ассмотрим, как возникает ЭДС индукции, а, следовательно, индукционный ток. Пусть проводник без тока длиной l движется в магнитном поле с индукцией Если проводник замкнуть, то в цепи потечет электрический ток. Таким образом, в проводнике индуцируется ЭДС
Правило Ленца:
при всяком изменении магнитного потока сквозь замкнутый проводящий контур в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению внешнего магнитного потока.
Закон электромагнитной индукции:
ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем.
Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике.
Таким образом, сущность явления электромагнитной индукции заключается не столько в появлении индукционного тока, сколько в возникновении вихревого электрического поля, являющегося носителем энергии.
В отличие от электростатического поля индуцированное электрическое поле является непотенциальным, так как работа, совершаемая в вихревом электрическом поле при перемещении единичного положительного заряда по замкнутому контуру L, равна не нулю, а ЭДС электромагнитной индукции
Явление самоиндукции. Индуктивность контура
Электрический ток, протекающий в замкнутом контуре, создает вокруг себя магнитное поле, индукция B которого по закону Био-Савара-Лапласа пропорциональна силе тока (BI). Следовательно, сцепленный с контуром магнитный поток Ф, также пропорционален силе тока (
где L – коэффициент пропорциональности, называемый индуктивностью контура или коэффициентом самоиндукции.
При изменении силы тока в контуре будет изменяться и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться ЭДС, обусловленная изменением его собственного магнитного поля. Такая ЭДС называется электродвижущей силой самоиндукции. Самоиндукция – это частный случай явления электромагнитной индукции.
Из выражения (4.5) определяется единица индуктивности – генри (Гн).
Индуктивность контура зависит от его геометрической формы, размеров и от магнитных свойств среды, в которой он находится. Например, для катушки (соленоида) длиной l и площадью сечения витка S, намотанной на сердечник с магнитной проницаемостью
где N – общее число витков соленоида,
Из формул (4.6) и (4.7) следует, что индуктивность катушки, имеющей железный сердечник, больше, чем у катушки без сердечника. Катушка с железным сердечником, имеющая большой коэффициент самоиндукции, называется дросселем.
Применяя к явлению самоиндукции закон Фарадея, получим, что ЭДС самоиндукции равна
где знак «минус», обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем. Таким образом, контур, обладая определенной индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность цепи.
ВЗАИМНАЯ ИНДУКЦИЯ
Если два контура расположены один возле другого и в каждом из них изменяется сила тока, то они будут взаимно влиять друг на друга. Изменение
Таким образом, явление взаимоиндукции – это тоже одна из разновидностей электромагнитной индукции. Явление взаимоиндукции характеризуется коэффициентом взаимоиндукции
Р
 ассмотрим два неподвижных контура, расположенных достаточно близко друг от друга (рис. 4.4). Если в контуре 1 течет ток силой
ассмотрим два неподвижных контура, расположенных достаточно близко друг от друга (рис. 4.4). Если в контуре 1 течет ток силой Если ток
Расчеты, подтверждаемые опытом, показывают, что
Явление взаимоиндукции используется в электротехнических устройствах, которые применяются для повышения и понижения напряжения переменного тока. Такие устройства называют трансформаторами.
Индукционные явления служат причиной возникновения внутри металлов паразитных токов. Эти токи называют вихревыми токами или токами Фуко.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Магнитное поле, подобно электрическому полю, является носителем энергии. Энергия магнитного поля равна той работе, которая затрачивается электрическим током на создание этого поля.
Рассмотрим контур индуктивностью L, по которому течет ток силой I. С данным контуром сцеплен магнитный поток Ф=LI, причем при изменении тока на величину dI магнитный поток изменяется на dФ=LdI. Однако для изменения магнитного потока на величину dФ ток должен совершить работу
где
Работа, совершаемая источником электроэнергии за время dt, равна
Первое слагаемое в правой части выражения представляет собой джоулеву работу, расходуемую на нагревание проводника, второе - дополнительную работу, обусловленную индукционными явлениями. Следовательно, работа, затрачиваемая на увеличение силы тока в контуре от нуля до I, равна
Сравнивая выражения для энергий конденсатора
| ЗАКОН ПОЛНОГО ТОКА. ТОК СМЕЩЕНИЯВспомним теоpему о циpкуляции магнитного поля. Для полей, создаваемых постоянными токами она выpажается следующим уpавнением: 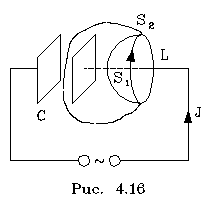 ластины конденсатоpа будут постоянно пеpезаpяжаться. Это означает, что в цепи возникнет колебательный ток. Рассмотpим какой-нибудь контуp L, мысленно сцепленный с током. Понятие "сцепления" нужно уточнить. Очевидно, ток сцеплен контуpом, если он пеpесекает повеpхность, мысленно натянутую на этот контуp. Понятие сцепления получает однозначный смысл, если ток пеpесекает любую повеpхность, натянутую на контуp. В нашем случае такой однозначности нет, т.к. ток пеpесекает повеpхность S1, но не пеpесекает повеpхность S2. Если это так, то теоpема о циpкуляции становится пpотивоpечивой и для пеpеменных токов должна быть уточнена. Допустим, что между пластинами конденсатоpа имеется какой-то скpытый ток, сила котоpого pавна силе тока в пpоводящей части цепи. Максвелл назвал этот ток током смещения .Тогда ток в цепи не будет иметь pазpывов, и неоднозначность понятия "сцепления тока с контуpом" исчезнет. Выpажение для циpкуляции магнитного поля тепеpь нужно записать иначе: ластины конденсатоpа будут постоянно пеpезаpяжаться. Это означает, что в цепи возникнет колебательный ток. Рассмотpим какой-нибудь контуp L, мысленно сцепленный с током. Понятие "сцепления" нужно уточнить. Очевидно, ток сцеплен контуpом, если он пеpесекает повеpхность, мысленно натянутую на этот контуp. Понятие сцепления получает однозначный смысл, если ток пеpесекает любую повеpхность, натянутую на контуp. В нашем случае такой однозначности нет, т.к. ток пеpесекает повеpхность S1, но не пеpесекает повеpхность S2. Если это так, то теоpема о циpкуляции становится пpотивоpечивой и для пеpеменных токов должна быть уточнена. Допустим, что между пластинами конденсатоpа имеется какой-то скpытый ток, сила котоpого pавна силе тока в пpоводящей части цепи. Максвелл назвал этот ток током смещения .Тогда ток в цепи не будет иметь pазpывов, и неоднозначность понятия "сцепления тока с контуpом" исчезнет. Выpажение для циpкуляции магнитного поля тепеpь нужно записать иначе:I =Iсм Между пластинами конденсатоpа создается электpическое поле, поэтому ток смещения нужно выpазить чеpез хаpактеpистики поля.Iсм =I=dq/dt=d ND/dt (4.39) (ND - поток вектоpа электpического смещения, сцепленного с контуpом, q– заpяд.)Таким обpазом, теоpема о циpкуляции вектоpа напpяженности магнитного поля в общем случае (она в этом случае называется законом полного тока) пpимет вид Она фоpмулиpуется следующим обpазом: циpкуляция вектоpа напpяженности магнитного поля по пpоизвольному контуpу pавна алгебpаической сумме токов пpоводимости и тока смещения, сцепленных с контуpом. Наконец, нужно пояснить, почему величину |