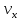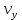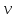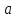Решение Уравнения движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключим время t из уравнений (1)
 Скачать 405.36 Kb. Скачать 405.36 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Уфимский государственный нефтяной технический университет Кафедра «Разработка и эксплуатация газовых и газоконденсатных месторождений» Расчетно-графическая работа К1 Кинематика точки Вариант 6 Проверил доцент кафедры МКМ Моисеев К. В. __________ Выполнил студент группы БГГ 21-02 Зарипов Д. И. __________ Уфа 2022 Дано: уравнения движения точки М  (1) (1)Найти: Необходимо установить вид траектории движения точки M и для момента времени t=t1=1c, найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории. Решение: Уравнения движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключим время t из уравнений (1). Получаем 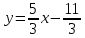 , ,  , y , y 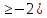 т.е. траекторией движения точки является прямая т.е. траекторией движения точки является прямаяВ момент времени t1=1c 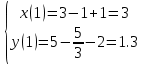  (рисунок 1.1) (Масштаб 1:1) Вектор скорости точки  (2) (2)Вектор ускорения 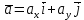 Здесь i, j – орты осей x и y, 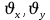 , , 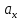 , ,  – проекции скорости и ускорения точки на оси координат. Найдем их, дифференцируя по времени уравнения движения (1), – проекции скорости и ускорения точки на оси координат. Найдем их, дифференцируя по времени уравнения движения (1), ; ;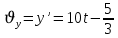 ; ;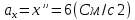 ; ;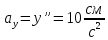 ;(3) ;(3)По найденным проекциям определяются модуль скорости 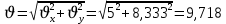 (См/с) (4) (См/с) (4)и модуль ускорения точки в момент времени t=t1=1c 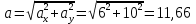 (См/с2) (5) (См/с2) (5)Модуль касательного ускорения точки 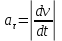 (6) (6)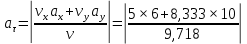 = 11,66 (См/c2) (7) = 11,66 (См/c2) (7)Здесь 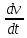 выражает проекцию ускорения точки на направление ее скорости. Знак «+» при выражает проекцию ускорения точки на направление ее скорости. Знак «+» при 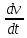 означает, что движение точки ускоренное, направления означает, что движение точки ускоренное, направления  и и  совпадают; знак «+» – что движение ускоренное. совпадают; знак «+» – что движение ускоренное.Модуль нормального ускорения точки 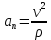 (8) (8)Если радиус кривизны траектории в рассматриваемой точке неизвестен, то  можно определить по формуле можно определить по формуле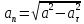 (9) (9)При движении точки в плоскости формула (8) принимает вид 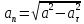 = 0(См/c2) (11) = 0(См/c2) (11)После того как найдено нормальное ускорение по формулам (8) или (9), радиус кривизны траектории в рассматриваемой точке определяется из выражения 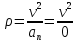 = = 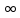 (12) (12)Результаты вычислений по формулам (3) – (5), (7), (11) и (12) для заданного момента времени t1=1 c приведены в таблице 1.1.
Таблица 1.1 | |||||||||||||||||||||||||||||||||||||||||||||