физон. Истоком и стоком тока соответственно. Такая двухполюсная система в проводящей среде, состоящая из истока и стока тока, называется
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Токовый диполь 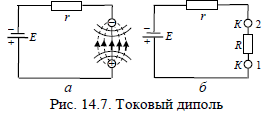 Если источник питания поместить в проводящую среду (солевой раствор), то клеммы источника будут полюсами диполя (рис. 14.7). Здесь R является эквивалентным сопротивлением проводя- щей среды, E – ЭДС ис- точника тока, r – его внутреннее сопротивление, 1 и 2 – соответственно исток и сток тока, К – электроды. В этом случае, несмотря на наличие тока I (электрические заряды стекают с полюсов) в про- водящей среде, диполь вследствие эффекта отсутствия экраниро- вания будет сохраняться. Ток движется в среде от положительного электрода к отрицательному. Эти электроды называют истоком и стоком тока соответственно. Такая двухполюсная система в проводящей среде, состоящая из истока и стока тока, называется дипольным электрическим генератором, или токовым диполем. Если источник питания поместить в проводящую среду (солевой раствор), то клеммы источника будут полюсами диполя (рис. 14.7). Здесь R является эквивалентным сопротивлением проводя- щей среды, E – ЭДС ис- точника тока, r – его внутреннее сопротивление, 1 и 2 – соответственно исток и сток тока, К – электроды. В этом случае, несмотря на наличие тока I (электрические заряды стекают с полюсов) в про- водящей среде, диполь вследствие эффекта отсутствия экраниро- вания будет сохраняться. Ток движется в среде от положительного электрода к отрицательному. Эти электроды называют истоком и стоком тока соответственно. Такая двухполюсная система в проводящей среде, состоящая из истока и стока тока, называется дипольным электрическим генератором, или токовым диполем.Д  ипольный момент токового диполя - вектор, направленный от стока (-) к истоку (+) и численно равный произведению силы тока на плечо диполя: Здесь ρ - удельное сопротивление среды. ипольный момент токового диполя - вектор, направленный от стока (-) к истоку (+) и численно равный произведению силы тока на плечо диполя: Здесь ρ - удельное сопротивление среды.Пусть в точке О в объеме электропроводной среды с удельным сопротивлением r (рис.5), находится отрицательный униполь точечного диполя с плечом L.
Расстояние r1 от положительного униполя диполя до точки А. Диполь и точка измерения потенциала находятся в электропроводной среде с удельным сопротивлением r. Потенциал электрического поля токового диполя в точке А равен алгебраической сумме потенциалов создаваемых в этой точке положительным и отрицательным униполем. Из треугольника ВОА следует, что Вынесем r из под корня Введем обозначение и тогда Потенциал поля в точке А будет представлен Функция может быть представлена многочленом, представляющим собой бесконечную сумму убывающих по величине членов, по степеням k. Тогда потенциал поля точечного диполя одиночного волокна может быть представлен в следующем виде где Q есть сумма членов пропорциональных Такое представление потенциала называется мультипольным разложением. Первый член разложения – потенциал создаваемый диполем, второй – электрической структурой квадруполем, третий – октуполем и т.д. Проанализируем эту формулу с точки зрения условий измерения потенциала. Пусть r >> L. В этом случае в формуле второй член мультипольного разложения очень мал по сравнению с первым членом. Остальные члены представляют собой члены еще более малой величины. Итак, при указанном условии измерения потенциала, можно считать, что электрическое поле одиночного волокна создается диполем, и потенциал рассчитывается по формуле Таким образом, дипольные представления об электрических свойствах одиночного волокна будут справедливыми, если размеры диполя будут очень малы по сравнению с расстоянием до точки измерения потенциала. Этот вывод является критерием справедливости дипольных представлений об элементарном генераторе тканей миокарда. Если r > l, то есть потенциал измеряется на расстоянии сравнимом с размерами диполя, то основной вклад в значение потенциала будут вносить такие электрические структуры как квадруполи, октуполи и т.д. Процессы деполяризации и реполяризации в целом миокарде протекают гораздо сложнее, чем в одиночном мышечном волокне. Электростатическое поле – электрическое поле, создаваемое в данной системе отсчета неподвижными электрическими телами или зарядами. Поле проявляет себя в том, что на помещенный в какую-либо его точку электрический заряд действует сила. Точечный пробный заряд – это такой заряд, собственным электрическим полем которого можно пренебречь (т.е. он не вызы- вает перераспределение зарядов, создающих поле и, следовательно, не искажает изучаемое с его помощью электростатическое поле). Напряженность электрического поля в данной точке – век- торная физическая величина, численно равная и совпадающая по направлению с силой F действующей со стороны поля на еди- ничный положительный заряд q0, помещенный в эту точку поля: , Принцип суперпозиции (наложения) полей формулируется так: Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых Б 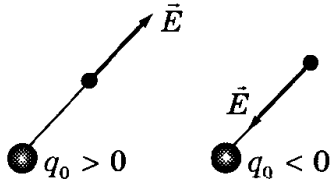 лагодаря принципу суперпозиции для нахождения напряженности поля системы заряженных частиц в любой точке достаточно воспользоваться выражением напряженности поля точечного заряда. лагодаря принципу суперпозиции для нахождения напряженности поля системы заряженных частиц в любой точке достаточно воспользоваться выражением напряженности поля точечного заряда.На рисунке ниже показано, как в точке A определяется напряженность поля 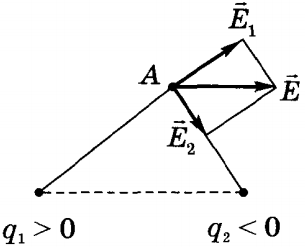 Потенциалом электростатического поля называется энергетическая характеристика поля, численно равная отношению потенциальной энергии пробного электрического заряда, помещённого в данную точку поля, к величине заряда.
Потенциал определяется с точностью до произвольной аддитивной постоянной, значение которой определяется разностью потенциалов в соседних точках поля. Подставив в (1.18) значениеWp из (1.17), получим для потенциала точечного заряда выражение:
где r – расстояние от данной точки до заряда q, создающего поле. Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями (ЭПП) – поверхностями, во всех точках кото- рых потенциал φ имеет одно и то же значение (в плоскости ри- сунка ЭПП изображаются линиями). Между двумя любыми точ- ками на эквипотенциальной поверхности разность потенциалов Δφ равна нулю. При перемещении заряда вдоль эквипотенциаль- ной поверхности работа А силами поля не совершается. Это возможно только при условии, что эквипотенциальные поверхно- сти во всех точках пространства перпендикулярны к линиям напряженности, т.е. вектор всегда нормален к эквипотенци- альным поверхностям (рис. 14.1). Эквипотенциальные по- верхности располагаются ближе между собой там, где напр я- женность поля выше F E Связь между потенциалом электростатического поля и его напряжённостью: Знак «минус» показывает, что вектор Е направлен в сторону убывания потенциала. Направление силовой линии (линии напряженности) в каждой точке совпадает с направлением. Потенциал поля системы точечных зарядов равен алгебраической сумме потенциалов полей, созданных каждым зарядом в отдельности. В этом заключается принцип суперпозиции потенциала электростатического поля. Если заряды распределены непрерывно по всему объёму, то потенциал поля равен:
|

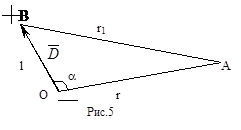
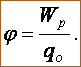
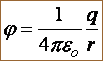 ,
,