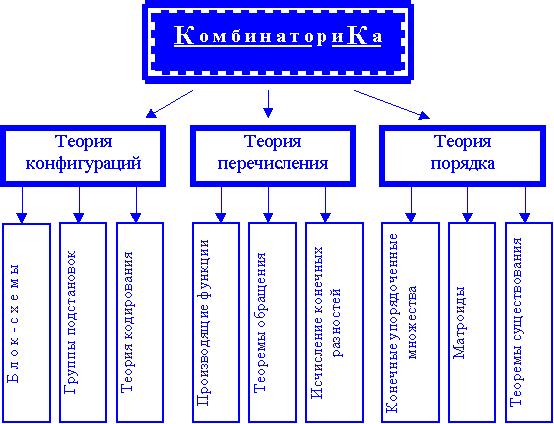
Теория комбинаторики. Историческая справка
 Скачать 416 Kb. Скачать 416 Kb.
|
Историческая справкаКомбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умели вычислять числа, которые сейчас называют "сочетания". В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из n слогов. Как научная дисциплина, комбинаторика сформировалась в XVII в. В книге "Теория и практика арифметики" (1656 г.) французский автор А. Также посвящает сочетаниям и перестановкам целую главу. Б. Паскаль в "Трактате об арифметическом треугольнике" и в "Трактате о числовых порядках" (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин "комбинаторика" стал употребляться после опубликования Лейбницем в 1665 г. работы "Рассуждение о комбинаторном искусстве", в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги "Ars conjectandi" (искусство предугадывания) в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в XIX в.Разрозненные комбинаторные задачи человечество решало с незапамятных времён. К концу XVI века накопились знания, относящиеся к:
- строит таблицы сочетаний до n = k = 12, после чего рассуждает о приложениях комбинаторики к логике, арифметике, к проблемам стихосложения и др. В течение всей своей жизни Лейбниц многократно возвращался к идеям комбинаторного искусства. Комбинаторику он понимал весьма широко, именно, как составляющую любого исследования, любого творческого акта, предполагающего сначала анализ (расчленение целого на части), а затем синтез (соединение частей в целое). Мечтой Лейбница, оставшейся, увы, неосуществлённой, оставалось построение общей комбинаторной теории.Комбинаторике Лейбниц предрекал блестящее будущее, широкое применение. В XVIII веке к решению комбинаторных задач обращались выдающиеся математики. Так, Леонард Эйлер рассматривал задачи о разбиении чисел, о паросочетаниях, о циклических расстановках, о построении магических и латинских квадратов. В 1713 году было опубликовано сочинение Я. Бернулли "Искусство предположений", в котором с достаточной полнотой были изложены известные к тому времени комбинаторные факты. "Искусство предположений" появилось после смерти автора и не было автором завершено. Сочинение состояло из 4 частей, комбинаторике была посвящена вторая часть, в которой содержатся формулы:
Для вывода формул автор использовал наиболее простые и наглядные методы, сопровождая их многочисленными таблицами и примерами. Сочинение Я. Бернулли превзошло работы его предшественников и современников систематичностью, простотой методов, строгостью изложения и в течение XVIII века пользовалось известностью не только как серьёзного научного трактата, но и как учебно-справочного издания. В работах Я. Бернулли и Лейбница тщательно изучены свойства сочетаний, размещений, перестановок. Перечисленные комбинаторные объекты относятся к основным комбинаторным конфигурациям . В математике в XIX веке появился сначала термин "геометрическая конфигурация" в лекциях по проективной геометрии профессора университета в Страсбурге К.Т. Рейе (1882).
разложения. Мур обогатил список известных комбинаторных конфигураций построением новых, обобщающих системы троек Штейнера, и системы троек Киркмана. Мур построил системы S[k, l, m], m
Комбинаторика, пройдя многовековой путь развития, обретя собственные методы исследования, с одной стороны, широко используется при решении задач алгебры, геометрии, анализа, с другой стороны, сама использует геометрические, аналитические и алгебраические методы исследования. В конце XVIII века учёные, принадлежащие комбинаторной школе Гинденбурга, попытались построить общую комбинаторную теорию, используя бесконечные ряды. Исследователи этой школы изучили большое количество преобразований рядов: умножение, деление, возведение в степень, извлечение корней, обращение рядов, разложение трансцендентных функций. Использование производящих функций в комбинаторике можно отнести к (уже) классическим традициям. В XX веке комбинаторика подверглась мощному процессу алгебраизации благодаря работам Дж.-К. Рота (1964), а затем Р. Стенли. Изучение ими частично упорядоченных множеств, свойств функции Мёбиуса, абстрактных свойств линейной зависимости, выявление их роли при решении комбинаторных задач способствовали обогащению комбинаторных методов исследования и дальнейшей интеграции комбинаторики в современную математику. Начало формы Конец формы Конец формы 1. Понятие множества. ПодмножестваПод множеством понимают объединение в одно целое объектов, связанных между собой неким свойством. Термин "множество" в математике не всегда обозначает большое количество предметов, оно может состоять и из одного элемента и вообще не содержать элементов, тогда его называют пустым и обозначают . Множество B называют подмножеством множества А, если любой элемент множества В является элементом множества А. Обозначается В А. 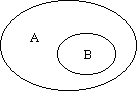 Свойства включения множеств:
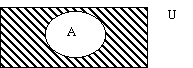
 Универсальное множество - это самое большее множество, содержащее в себе все множества, рассматриваемые в данной задаче. На диаграмме Эйлера - Венна универсальное множество обозначают в виде прямоугольника и буквы U:  2. Операции над множествами |
| n | | | | | | | | | | | |
| 0 | 1 | | | | | | | | | | |
| 1 | 1 | 1 | | | | | | | | | |
| 2 | 1 | 2 | 1 | | | | | | | | |
| 3 | 1 | 3 | 3 | 1 | | | | | | | |
| 4 | 1 | 4 | 6 | 4 | 1 | | | | | | |
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | | | | | |
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | | | | |
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | | | |
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | | |
| 9 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |
| 10 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
Заметим, что Блез Паскаль называл числовой треугольник, начало которого содержится в таблице1, арифметическим. Паскаль посвятил свойствам арифметического треугольника основополагающий "Трактат об арифметическом треугольнике" (1654). Справедливости ради, стоит упомянуть, что биномиальные коэффициенты были хорошо известны в Азии за много веков до рождения Паскаля. В Италии треугольник Паскаля называют треугольником Тартальи.
Сочетания имеют многочисленные интерпретации и приложения. Сочетания
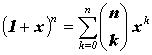 (1.4)
(1.4) В этой интерпретации индексы могут принимать вещественные значения. Используя свойства биномиальных коэффициентов (при разных ограничениях на выбор верхних и нижних индексов), доказано громадное число комбинаторных тождеств, составивших самостоятельный раздел комбинаторной математики. В частности, из формулы 1.4 при x = 1, получим
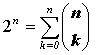 , при
, приx = -1, n > 0, получим
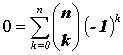 , продифференцировав равенство 1.4, получим при x = 1,
, продифференцировав равенство 1.4, получим при x = 1, 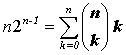 и т.д.
и т.д. Существует тесная связь между подмножествами множества и разложениями целого (положительного) числа. Разложение n есть представление числа n в виде упорядоченной суммы положительных целых чисел. Например, существует восемь разложений числа 4, именно:
1+1+1+1 3+1
2+1+1 1+3
1+2+1 2+2
1+1+2 4
Если разложение
(k - 1)-подмножество
Эта формула устанавливает биекцию между всеми k-разложениями числа n и (k - 1)-подмножествами (n - 1)-множества.
Следовательно, существует
x1 + x2 + …+ xk = n (1.6)
Неотрицательные целые решения уравнения 1.6 называются слабыми k-разложениями числа n. Число неотрицательных целых решений уравнения 1.6 равно числу положительных решений уравнения
y1 + y2 + … + yk = n + k,
то есть числу k-разложений числа n + k. Таким образом, N(n,k) =
Если k-сочетание содержит повторяющиеся элементы, то такое k-сочетание называют
k-мультимножеством. Число всех k-сочетаний с повторениями из данного n-элементного множества обозначим через
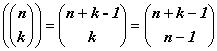 (1.7)
(1.7) Сочетание
Обозначим символом
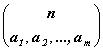 (1.8)
(1.8) число способов распределения n элементов среди категорий C1, C2, … Cm так, чтобы категории Ci принадлежало точно ai элементов. Тогда
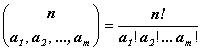 (1.9)
(1.9) Блок-схемы
Комбинаторные конфигурации наиболее общего вида были исследованы в 30-е годы XX столетия и были названы блок-схемами (block design). Блок-схемы состоят из наборов элементов, называемых блоками. Выбор элементов и пар элементов в блоки подчиняются определённым правилам.
Уравновешенной неполной блок-схемой называется такое размещение v различных элементов по b блокам, что каждый блок содержит точно k различных элементов, каждый элемент появляется точно в k различных блоках и каждая пара различных элементов ai , ajпоявляется точно в
Множество всех
bk = vr (1.10)
r (k - 1) = (v - 1) (1.11)
Частным случаем блок-схем являются так называемые конечные плоскости. Выберем конечное множество P. Элементы из P назовём точками. Некоторые подмножества из P назовём прямыми. Пусть отношение инцидентности между точками и прямыми удовлетворяет следующим геометрическим аксиомам.
На каждой прямой лежит n точек B.
Через каждую точку проходят n прямых.
Любые две прямые пересекаются в одной точке.
Через любые две точки проходит единственная прямая.
Существуют 4 точки неколлинеарные по три.
Тогда конечное множество P точек и множество L прямых образует конечную проективную плоскость.
Пример:
P = {1, 2, 3, 4, 5, 6, 7}.
L = {l1, l2, l3, l4, l5, l6, l7}
l1 = {1, 2, 3}, l2 = {3, 4, 5}, l3 = {1, 5, 6}, l4 = {1, 4, 7}, l5 = {2, 5, 7},
l6 = {3, 6, 7}, l7 = {2, 4, 6}.
Размещения с повторениями (n различных элементов, элементы могут повторяться):
Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в наборе не повторяются; 2) буквы могут повторяться?
1) Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА.
2) Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА.
Перестановки c повторениями (k различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 + … + mk = n, где n - общее количество элементов):
Пример. Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза?
1) Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА.
2) Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.
Сочетания c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться):
Пример. Возьмем плоды: банан (Б), ананас (А) и репа (Р). Какие сочетания из этих плодов, взятых по два, можно получить? Сколько таких наборов получится, если: 1) плоды в наборе не повторяются; 2) можно брать по два одинаковых плода?
1) Получатся наборы: БА ("банан, ананас" и "ананас, банан" - один и тот же набор), АР и РБ.
2) Получатся наборы: ББ, БА, БР, АА, АР, РР.
Вопросы
1. Приведите примеры множеств и их подмножеств.
2. Проиллюстрируйте примерами "из жизни" пересечение, объединение и разность множеств.
3. Постройте диаграммы Эйлера - Венна на свойства разности и дополнения множеств.
4. Назовите виды комбинаций, где важен порядок при составлении наборов и где он не важен.
Список литературы
Айгнер М. Комбинаторная теория. М.: Мир, 1982.
Стенли Р. Перечислительная комбинаторика. М.: Мир, 1990.
Холл. М. Комбинаторика. М.: Мир, 1970.
Грэхем Р., Кнут Д., Паташник О. Конкретная математика. М.: Мир, 1998.
Рыбников К.А. Введение в комбинаторный анализ. М: МГУ, 1985.
Рыбников К.А. История математики. М.: МГУ, 1994.
Бородин А.И., Бугай А.С. Биографический словарь деятелей в области математики. Киев: Ряданська школа, 1979.
Клейн Ф. Лекции о развитии математики в XIX столетии. М.: Наука, 1989.
История математики с дрвнейших времён до начала XIX столетия / Под ред. А.Н. Колмогорова, А.П. Юшкевича. М: Наука, 1970-1972. T.1-3.
История возникновения и развития комбинаторки: www.combinatorics.by.ru/stories.htm
Задачи по комбинаторике:
www.math.omsu.omskreg.ru/info/learn/terver/3(001).htm
Библиотека алгоритмов. Комбинаторика:
alglib.dore.ru/combin/index.html#salman
Введение в комбинаторику:
combinatorika.narod.ru
Биография Лебница Готфрида Вильгельма:
www.math.rsu.ru/mexmat/polesno/leibn.ru.html
schools.techno.ru/sch444/MUSEUM/1_17_119.htm
historyvt.narod.ru/leibnic.htm
Готфрид Вильгельм Лейбниц
Элиаким Гастингс Мур
Джеймс Джозеф Сильвестр
Данный сайт был создан Колпаковой Анной - студенткой 6 курса (магистратуры) факультета информатики и экономики Пермского государственного педагогического университета 2002 г.
Сайт Пермского государственного педгогического универмитета: www.pspu.ac.ru
http://www.problems.ru/view_by_subject_new.php?parent=189&start=30
Конец формы





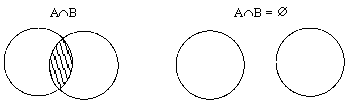

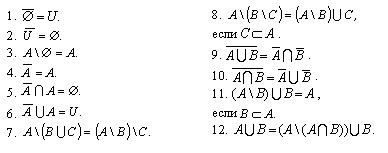
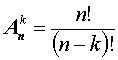 . (2)
. (2) 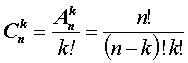
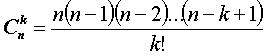 (3)
(3)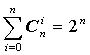
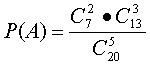 .
.