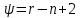Исторический очерк. Термодинамика 1) движение тепла (дословный перевод) 2) наука о движущих силах
 Скачать 91.17 Kb.
|
|
Термодинамика: основные понятия и определения. Предмет и объект изучения термодинамики. Термины. Термодинамические параметры. Краткий исторический очерк. Термодинамика –1) «движение тепла» (дословный перевод); 2) наука о «движущих силах», возникающих при тепловых процессах (более точно); 3) наука, изучающая законы превращения энергии в различных процессах, сопровождающихся тепловыми эффектами; 4) наука о закономерностях превращения энергии. Термодинамика –дедуктивная наука (используя ограниченный набор утверждений, можно вывести дедукцией все основные положения термодинамики); феноменологическая теория макроскопических процессов, сопровождающихся превращениями энергии. Основывается на экспериментально установленных законах, получивших название начал термодинамики: 1-ое начало выражает закон сохранения (и превращения) энергии, 2-ое начало определяет направленность термодинамических процессов. Термодинамика подразделяется на техническую, физическую, химическую и т.д. Краткий исторический обзор. Термодинамика возникла из потребностей теплотехники. Во второй половине XVIII века промышленный переворот в Англии позволил технически решить задачу создания универсального двигателя, производящего работу за счет теплоты горения топлива; распространяются тепловые машины (их появление связывают обычно связывают с деятельностью Джеймса Уатта; первый патент был получен им в 1769 г.) Новая наука – термодинамика – возникла в начале XIX века. Основные задачи, которые перед ней были поставлены: 1)установление количественной связи между теплотой и работой; 2)повышение эффективности паровых машин, использующихся в промышленности. 1824 г. – Сади Карно опубликовал трактат «Размышления о движущей силе огня и о машинах, способных развивать эту силу». Термин «движущая сила огня» в современной трактовке означает работу. Доказывается, что работа зависит от температур горячего и холодного источников тепла; утверждается, что более эффективными являются паровые машины высокого давления; указывается, что причиной потери работоспособности является «бесполезное восстановление равновесие теплорода». Таким образом, несмотря на использование неверной теории теплорода в этой работе сформулированы основные законы термодинамики – I и II начала. 1842 г. – Майер устанавливает связь между теплотой и работой, определяет механический эквивалент теплоты (неточно). 1843 г. – Джоуль, проведя уникальные по точности эксперименты, находит тепловой эквивалент работы (значение этой величины и сейчас практически такое же). Работы Майера и Джоуля устанавливают частный случай I–го начала термодинамики. 1854 г. – Клаузиус вводит новую функцию состояния – энтропию S, рассматривая обратимый круговой процесс. Дифференциал энтропии dS связывается с малым приращением теплоты dQ: dS=dQ/T. Тем самым он устанавливает II-ое начало термодинамики для обратимых процессов. (То, что энтропию можно использовать для необратимых процессов, показал М. Планк). Томпсон (лорд Кельвин) вводит понятие абсолютной температуры (термодинамической) температуры. В работах Гиббса разрабатывается метод термодинамических потенциалов для исследования ТДП; определяются условия термодинамического равновесия и фазовых переходов. 1906 г. – теорема Нернста – опытный факт, дополняющий I и II начала термодинамики; иногда называют III-им началом; ее можно также вывести из основных положений статистической физики. Теорема Нернста: При температуре, стремящейся к абсолютному нулю, равновесные изотермические процессы протекают без изменения энтропии:  .В этом случае энтропия перестает быть функцией состояния и стремится к некоторой постоянной величине, не зависящей от параметров состояния. Д.И.Менделеев ввел понятие критической температуры Ткр- при этой температуре поверхностное натяжение равно нулю; пропадает различие между жидкостью и паром. Сам Менделеев назвал ее «температурой абсолютного кипения». Изучением критических явлений занимались также А.Г.Столетов и М.П.Авенариус. Термодинамикой излучения занимались В.А. Михельсон и Б.Б. Голицын; последний ввел понятие температуры излучения. Применение термодинамики в физической химии рассматривалось в работах Д.П. Коновалова и Н.С. Курнакова. В минувшем веке российские ученые немало сделали для развития термодинамики: Л.Д.Ландау – теория фазовых переходов, М.А.Леонтович – термодинамические функции неравновесных состояний, Н.Н.Боголюбов – работы по теории сверхтекучести и сверхпроводимости. Основные понятия, определения, термины. Объект изучения – любые тела, входящие в т.н. «термодинамическую систему» (ТДС). Термодинамическая система (ТДС) – совокупность макротел, находящихся между собой и окружающей средой в тепловом и механическом взаимодействии.Эта термодинамическая система должна быть 1) достаточно обширной и сложной, чтобы в ней выполнялись статистические закономерности, то есть система должна состоять из достаточно большого количества частиц (т.к. параметры, которыми характеризуется состояние ТДС – температура и давление – это результат статистического осреднения по большому числу частиц: температура – мера средней кинетической энергии молекул, давление – характеризует средний импульс молекул; по нескольким молекулам осреднение недостоверно); 2) ограниченной, то есть число частиц в ней должно быть конечно; иными словами, должно быть нечто, оставшееся за пределами системы, то что называется «окружающей средой» (ОС) - объекты материального мира, не входящие в термодинамическую систему. Предмет изучения: -закономерности превращения энергии в процессах взаимодействия рабочих тел с элементами энергетических машин и с ОС; - анализ совершенства энергомашин; - изучение свойств рабочих тел и их изменений в процессах взаимодействия. ТДС может быть открытой (через границы системы проходит поток массы) или закрытой (замкнутой). Границы ТДС могут быть подвижными или неподвижными. Напомним, что ТДС должна быть 1) достаточно сложной, но при этом 2) ограниченной. Адиабатическая термодинамическая система – ТДС не обменивается теплотой с окружающей средой. Изолированная термодинамическая система – ТДС не обменивается с ОС ни теплотой, ни работой (т.е. не обменивается энергией). Гомогенная термодинамическая система – свойства вещества или неизменны во всех точках системы (это т.н. однородная система), или плавно изменяются в поле действия массовых сил. Гетерогенная термодинамическая система – состоит из подсистем с различными свойствами. Считается, что на границах подсистем физические свойства меняются скачком (на самом деле изменение свойств происходит постепенно, но на малом расстоянии порядка длины свободного пробега молекул). Окружающая среда (ОС) – объекты материального мира, не входящие в ТДС. Разделение на ТДС и ОС условно (по нашему усмотрению). Рабочее тело – любая среда, которая используется для преобразования энергии.Термодинамический метод исследования: 1)рассматривают большое, но конечное число частиц, составляющих систему; 2)не изучают процессы на молекулярном уровне; 3)оперируют макровеличинами – термодинамическими параметрами. Термодинамические параметры. Это макровеличины, характеризующие состояние ТДС. Их очень много; традиционно в первую очередь выделяют т.н. «термические» параметры: объем, давление, температуру. Объем V [м3] – характеризует пространство, занимаемое ТДС. Тесно связан с параметрами энергетического взаимодействия. В международной системе единиц измеряется в м3. Часто используется удельный объем v = V/m [м3/кг] (*)- объем единицы массы вещества. Наряду с удельным объемом используется обратная ему величину - плотность r=1/v (**). По (*) всегда можно определить удельный объем, т.к. ТДС всегда занимает некоторое пространство (имеет ненулевой объем), и в этом объеме всегда содержится некая конечная масса, тогда как (**) имеет более ограниченное применение, поскольку говорить о плотности как о макровеличине (единой, глобальной для всей ТДС) можно только для однородных систем. Давление p [Па=Н/м2]– характеризует силовое (механическое) взаимодействие элементов системы друг с другом и с ОС; p=F/f, F – сила, f – площадь поверхности, к которой приложена сила. Помимо основной единицы измерения – Паскаль, существует много дополнительных и внесистемных единиц измерения давления (техническая и физическая атмосфера, бар, дина, мм ртутного, водяного и спиртового столба и т.д.) Различают абсолютное давление ра (измеряется в абсолютных атмосферах ата) и избыточное давление ри (измеряется в избыточных атмосферах ати); ра= ри+В, B – барометрическое давление ОС. Температура T [К] – в молекулярной и статистической физике ее считают мерой средней кинетической энергии молекул. Но термодинамика не оперирует понятиями о структуре вещества, поэтому для нее такое определение не годится. Температура в термодинамике считается мерой нагретости тела. Если два тела привести в соприкосновение, то они могут (но не обязаны) обмениваться энергией. Если первое тело при этом будет отдавать энергию, считаем его температуру более высокой, чем у второго и наоборот. Если энергообмен не происходит, считаем температуру тел одинаковой. В системе единиц СИ температура измеряется в Кельвинах. По шкале Кельвина начало отсчета – абсолютный ноль; точка таяния льда @273.15 К. Кроме шкалы Кельвина существуют также шкалы Цельсия, Фаренгейта, Реомюра, Ренкина. Если в формуле или уравнении температура обозначена Т, то это абсолютная температура в Кельвинах, если t – имеется в виду температура в градусах Цельсия 0С. Термодинамический процесс. Если в разных частях ТДС термические параметры неодинаковы, то состояние системы называют неравновесным. Далее, если это специально не оговорено, будем считать, что во всех точках системы параметры выровнены. Если, кроме того, система находится в равновесии с ОС, то все параметры системы неизменны во времени, взаимодействие в системе прекращается; состояние системы при этом называется равновесным. На самом деле с течением времени каждый параметр, например температура Т, может слегка отклоняться от своего среднего значения  . Эти отклонения называются флуктуациями. Они весьма малы по сравнению со средними значениями и в рамках термодинамического метода не рассматриваются.Если изменение хотя бы одного параметра заметно превышает уровень флуктуаций, говорят о термодинамическом процессе. Термодинамический процесс ТДП – совокупность последовательных состояний ТДС. ТДП делятся на равновесные и неравновесные. Равновесный ТДП – последовательность равновесных состояний ТДС. В каждый момент равновесного процесса ТДС находится в равновесии.Неравновесный ТДП – при изменении состояния равновесие в системе нарушается. Термическое уравнение состояния. Термодинамическая поверхность.Диаграммы состояния.Состояние ТДС можно определить, задав несколько термодинамических параметров, например, термические: p,V,T. Сколько же параметров необходимо, чтобы однозначно определить состояние ТДС? Очевидно, что одного параметра мало: скажем, система, состоящая из воды  при температуре t=120 может представлять из себя жидкость (при р = 5 МПа), пар (при р = 0.1 МПа) или смесь пара с жидкостью с переменными свойствами (при р = 0.2 МПа). В последнем случае ТДС является неоднородной (двухфазной).Установлено, что в однородных ТДС любые два термических параметра однозначно определяют третий, а совокупность трех термических параметров, в свою очередь, полностью определяет состояние ТДС в целом. Термодинамика постулирует наличие уравнения состояния, но не определяет его вид. Вид уравнения зависит от рабочего тела и определяется либо на основе опытных данных, либо методами статистической физики. Уравнение (***) определяет некую поверхность в координатах (p-V-T) – т.н. термодинамическую поверхность. Эту поверхность, в принципе, можно нарисовать. Но пользоваться трехмерным изображением неудобно, поэтому обычно используется метод сечений: фиксируется один из параметров (например, выбирается некая фиксированная T=const), при этом получается семейство двумерных кривых в координатах p-V. Каждая кривая соответствует некоторой постоянной температуре. Графики, построенные таким образом в двумерных координатах p-V, p-T, V-T и т.п. называются диаграммами состояния (например, p-V – диаграмма). Термодинамический процесс ТДП обозначается на диаграмме состояния линией, идущей из начальной точки (исходное состояние системы) в конечную (итоговое состояние системы). ТДП, у которого начальная точка совпадает с конечной (ТДС возвращается в исходное состояние, линия процесса на диаграмме состояния замкнута) называется циклом. Связь термических параметров задается формулами вида: V = V(p,T) = f1(p,T), p = p(V,T) = f2(V,T), T = T(p,V) = f3(p,V), или, объединяя все три равенства: F(p,V,T)=0 (***). Выражение (***) называют термическим уравнением состояния. Правило фаз Гиббса В общем случае количество независимых параметров, необходимых для однозначного определения состояния системы, определяется правилом Гиббса:
ψ - число степеней свободы, т.е. число независимых параметров, необходимых для описания системы, r - число компонентов, n- число фаз. Для однородной системы (один компонент, одна фаза) получаем: ψ=1-1+2=2. Правило Гиббса хорошо иллюстрирует т.н. фазовая pt-диаграмма: Рассмотрим какое-либо чистое вещество (т.е. r =1). Фазовая диаграмма показывает, когда это вещество будет находиться в твёрдом, когда в жидком, а когда в газообразном состоянии, и как будут происходить фазовые переходы. При малых температурах вещество пребывает в твёрдом состоянии (область левее линии DAB). При высоких температурах вещество пребывает в газообразном (пар) состоянии (область правее линии DAC). Область, ограниченная BA и AC, соответствует жидкой фазе. При низких давлениях с ростом температуры происходит переход твёрдой фазы в газ (пар) - возгонка, с уменьшением температуры – переход газовой фазы в твёрдую – сублимация, изображённые линией e-f-g. При высоких давлениях с ростом температуры вещество сначала переходит из твёрдой фазы в жидкую (плавится), а затем из жидкой в газообразную (кипит) – линия a-b-c-d. Жирным обозначены линия сублимации (возгонки) AD, линия плавления (кристаллизации) AB, линия кипения (конденсации) AC. Линии сублимации и плавления AD и ABформально уходят в бесконечность (не имеют конца), линия кипения AC заканчивается в точке C – критической точке. Выше точки C находится т.н. закритическое состояние вещества, когда нет различия между паром и жидкостью. На линиях сублимации, плавления и кипения одновременно сосуществуют две фазы: жидкая и твёрдая на линии плавления, твёрдая и газообразная на линии сублимации, жидкая и газообразная на линии кипения. В точке A одновременно сосуществуют три фазы (твёрдая, жидкая и газообразная) – это главная тройная точка. У многих веществ есть несколько тройных точек, потому что жидкая и газообразная фазы – единственные, а твёрдых может быть несколько – это т.н. аллотропные модификации: белое и серое олово, α- и γ- и δ- железо, углерод в форме графита, алмаза, графена и т.д., около 20 разновидности водяного льда. Поэтому возможно существование тройных точек, в которых сходятся две твердые фазы и одна жидкая или три твёрдых фазы. Но главная тройная точка всегда одна. 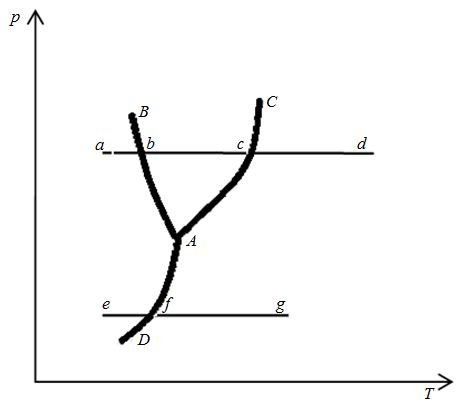 Рис.1 Фазовая диаграмма Применяем правило Гиббса: - в однофазных областях: r=1,n =1,ψ=1-1+2=2. Для описания состояния твёрдой фазы, или жидкой, или газообразной необходимо задать два параметра: температуру и давление. На пересечении горизонтали p=const и вертикали T=const получаем точку – состояние вещества; - на линиях фазовых переходов AD, AB, AC сосуществуют две фазы: r=1,n =2,ψ=1-2+2=1. То есть мы задаём либо температуру, либо давление, а второй параметр не является независимым, определяется с графика. И действительно, если мы задаём, допустим, давление (атмосферное), то мы уже не можем выбирать температуры плавления и кипения вещества: вода при атмосферном давлении превращается в лёд при t=00C, кипит при t≈1000C; - в тройной точке сосуществуют три фазы одновременно: r=1,n =3,ψ=1-3+2=0. Это значит, что мы не можем самостоятельно задать ни одного параметра: тройная точка у данного чистого вещества такая, какой её определили природа. У воды параметры главной тройной точки: t=0.010C (T=273.16 K), p=610.8 Па v=0.001002 м3/кг. Идеальный газ. Термическое уравнение состояния идеального газа – уравнение Клапейрона – Менделеева. Идеальный газ – простая и удобная модель реального вещества в газообразном состоянии, которая предполагает, что молекулы имеют массу, но не имеют собственного объёма, т.е. представляют собой материальные точки. Взаимодействием между ними можно пренебречь. Реальный газ «похож» на идеальный, если он достаточно разрежен. Тогда расстояние между молекулами много больше (на много порядков), чем размеры самих молекул, что и позволяет считать молекулы материальными точками. Если же газ сильно сжат, давление в нём составляет несколько десятков или сотен атмосфер, и, соответственно, велика его плотность, то молекулы сближаются друг с другом, и их собственными размерами уже нельзя пренебречь в сравнении с расстояниями между ними, как нельзя и полностью пренебречь взаимодействием между молекулами. Кроме того, модель идеального газа «не работает» при низких температурах: идеальный газ формально остаётся газом вплоть до абсолютного нуля, сжимаясь при этом в точку: 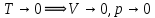 , тогда как реальный газ при низких температурах превращается в жидкость. Таким образом, модель идеального газа не описывает переход газа в жидкость (конденсацию).При давлении, меньшем или равном атмосферному, и «комнатных» температурах большинство газов можно с достаточной точностью считать идеальными. Можно также сказать, что идеальный газ – это такой газ, который подчиняется уравнению состояния Клапейрона – Менделеева (это уравнение также называют термическим уравнением состояния идеального газа):
p - давление газа, [Па]; V - объём, занимаемый газом, [м3]; m - масса газа [кг]; R0- универсальная газовая постоянная, 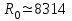 [Дж/(кмоль К)];µ - молярная (мольная) масса газа, т.е. масса 1 моля или, как в данном случае, киломоля вещества [кг/кмоль]; T- абсолютная температура [К]. Часто используются и другие формы записи уравнения Клапейрона – Менделеева:
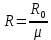 , [Дж/(кг К)] - индивидуальная газовая постоянная (для данного газа const, но у разных газов отличается) или форма записи через удельный объём::
Покажем, как определять молярную массу и находить индивидуальную газовую постоянную на примере некоторых газов. Если газ одноатомный (He, Ar и т.п.), то в Периодической таблице элементов Менделеева смотрим атомное число соответствующего элемента (у гелия атомное число 4.00260, для наших расчётов можно округлить до 4; у аргона атомное число 39.94, можем округлить до 40). Полученное число и будет молярной массой, измеренной в кг/кмоль (или г/моль): µHe=4 кг/кмоль, µAr=40 кг/кмоль. Индивидуальные газовые постоянные гелия и аргона: RHe=8314/4=2078.5 Дж/(кг К), RAr=8314/40=207.85 Дж/(кг К). Если газ двух- или многоатомный, нужно по таблице Менделеева определить атомные числа элементов, составляющих молекулу газа, и сложить их; при этом, если в молекуле, скажем, 2 атома данного элемента, то атомное число элемента нужно умножить на два. Атомные числа кислорода 15.999 (берём 16), азота 14.0067 (берём 14), углерода 12.011 (берём 12), серы 32.06 (берём 32), так что µO2=2·16=32 кг/кмоль, µN2=2·14=28 кг/кмоль, µCO=12+16=28 кг/кмоль, µCO2=12+2·16=44 кг/кмоль, µSO2=32+2·16=64 кг/кмоль. RO2=8314/32=259.8 Дж/(кг К), RN2= RCO=8314/28=296.9 Дж/(кг К) и т.д. Смесь идеальных газов. Характеристики состава смеси. Парциальные давления и объёмы. Определение молярной массы смеси. Будем считать, что смесь нескольких идеальных газов также является идеальным газом (что вполне логично: если молекулы идеального газа не взаимодействуют между собой, как бы не замечают друг друга, то точно так же они не замечают и молекулы другого идеального газа, находящегося в том же объёме). Назовём газы, составляющие смесь, компонентами смеси. Пусть смешали n компонентов, каждый из которых считается идеальным газом. Пронумеруем их от 1 до n. Будем величинам, относящимся к данному компоненту, присваивать индекс i (i=1, 2, ..n), а величины, относящиеся к смеси в целом, оставлять без индекса. Введём: T [K] - температура смеси, совпадающая с температурой всех компонентов, m1, m2, …,mi,…, mn [кг] - массы компонентов до смешения (останутся такими же и после смешения); 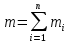 - масса всей смеси;µ1, µ2, …,µi,…, µn [кг/кмоль] - молярные массы компонентов смеси; µ - молярная масса смеси (пока не знаем, как её определить); 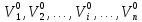 [м3] - объёмы компонентов до смешения;V- объём образовавшейся смеси (не равен сумме исходных объёмов компонентов: 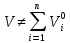 ); 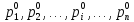[Па] - давления компонентов до смешения;p- давление образовавшейся смеси (не равно сумме исходных давлений компонентов: 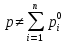 );M1, M2, …,Mi,…, Mn -число молей компонентов до (и после) смешения; М - число молей вещества в смеси: 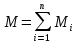 ;R1, R2, …,Ri,…,Rn [Дж/(кг К)] - газовые постоянные компонентов, Ri= R0/µi; R= R0/µ - газовая постоянная смеси. Чтобы охарактеризовать состав смеси, введём массовые и мольные доли компонентов. Массовая доля компонента в смеси γi - отношение массы компонента к общей массе смеси:  - безразмерная величина, выражается в долях единицы.Сумма всех массовых долей компонентов смеси равна 1 (говорят: «нормирована на единицу»): 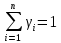 .Мольная доля компонента в смеси Ni - отношение числа молей компонента к числу молей смеси:  - безразмерная величина, выражается в долях единицы.. Мольные доли всех компонентов смеси также нормированы на единицу: 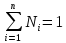 . .Всегда можно выразить мольную долю компонента через массовую и наоборот: 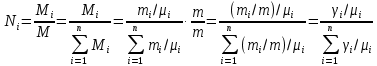 . (a)Здесь выразили число молей компонента, поделив его массу на массу одного моля этого компонента, а также учли, что константу (в данном случае общую массу смеси m) можно вносить под знак суммы. Аналогично: 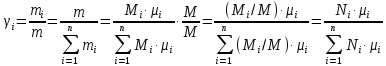 . (b)Введём понятие парциального давления компонента в смеси. Пусть имеется смесь идеальных газов, например, воздух в комнате, который можно приближённо рассматривать состоящим из азота N2 и кислорода O2 (несколько более точный состав – азот, кислород, аргон, углекислый газ и водяной пар, причём последние три газа в сумме составляют около 1% состава по объёму). Давление воздуха в комнате – одна атмосфера. Часть этого давления создают молекулы азота, часть – кислорода (на азот приходится около 0.78 атмосферы, на кислород – 0.21 атмосферы, на остальные газы – 0.01 атмосферного давления). Парциальное давление компонента pi – это доля в общем давлении смеси p, вносимая данным компонентом. Для идеальных газов выполняется закон Дальтона :  .Сумма парциальных давлений компонентов равна общему давлению смеси. (Для реальных газов закон Дальтона выполняется приближённо; обычно записывают: 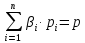 , где βi - поправочные коэффициенты, выражающие взаимное влияние газов смеси друг на друга). Можно ввести также понятие парциального объёма компонента в смеси. Проведём мысленный опыт с воздухом (N2 +O2) в нашей комнате. Оба компонента занимают весь объём помещения V, при этом каждый газ имеет своё парциальное давление pi , которые в сумме дают атмосферное давлениеp. Поддерживая температуру постоянной (т.е. проводя изотермический процесс T=const), разделим газы: поймаем каждую молекулу «за хвост» и растащим в разные углы комнаты – молекулы азота в одну сторону, а молекулы кислорода – в другую. После чего каждую группу молекул сожмём, доведя давление и азота, и кислорода до того давления p, которое было у смеси в целом (т.е. до атмосферного). Таким образом, сначала газы занимали общий объём V и имели каждый своё (парциальное) давление pi, а теперь каждый газ имеет одинаковое давление p, но занимает свой объём Vi, а температура при этом не менялась. Объём Vi и называется парциальным или собственным объёмом компонента в смеси. При помощи уравнения состояния Клапейрона – Менделеева наш умозрительный опыт для каждого газа – компонента смеси можно записать так: 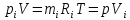 .Отсюда следует, что 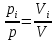 .Также очевидно, что закон Дальтона можно записать и через парциальные объёмы: 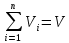 .Введём теперь ещё одну характеристику состава смеси – объёмную долю компонента. Объёмная доля компонента в смеси ri – отношение парциального давления этого компонента к общему давлению смеси или отношение парциального объёма к общему объёму:  .Объёмные доли всех компонентов также в сумме составляют единицу:  .Покажем, что для идеального газа объёмная доля совпадает с мольной. Учтём, что парциальный объём Vi можно представить как произведение удельного объёма компонента vi на его массу mi: Vi =vi ·mi, а массу компонента выразить через массу одного моля и число молей: mi =µi ·Mi:  . Величина в скобках - это объём одного кмоля компонента. Но известно, что один кмоль любого идеального газа занимает один и тот же объём – объём Авогадро, VА=22.4м3, так что можно продолжить: 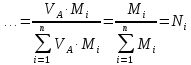 .Теперь мы можем характеризовать состав смеси массовыми, объёмными или мольными (совпадающими с объёмными) долями компонентов, а также пересчитывать одни доли в другие: 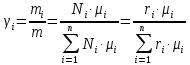 ,  .Определим теперь молярную массу смеси µ. Эту величину ещё называют кажущейся молярной массой смеси в том смысле, что в смеси есть газы с разными µi, и нет ни одного газа, мольная масса которого была бы равна µ, но «в среднем» по смеси получается именно такая величина. Запишем уравнение состояние идеального газа (Клапейрона – Менделеева) для i-того компонента, используя понятие парциального давления, т.е. считая, что газы смеси занимают общий объём, но каждый имеет своё парциальное давление (можно с тем же успехом рассуждать, используя понятие парциального объёма): 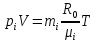 .Запишем такое уравнение для каждого компонента, а затем просуммируем, вынося за знак суммы общие давление и температуру и универсальную газовую постоянную:  .Но по закону Дальтона , так что в левой части равенства получаем pV: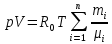 . (c)Но, с другой стороны, можно записать уравнение Клапейрона – Менделеева для смеси в целом: 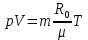 . (d)Левые части (c) и (d) совпадают, следовательно, равны и правые: 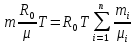 ,  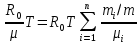, откуда получаем для молярной массы смеси: .Можно определить µ и через мольные (объёмные) доли компонентов. Используем выражения (a) и (b): 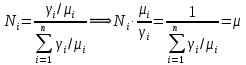 , 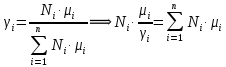Следовательно,  .Индивидуальную газовую постоянную смеси можно определить через молярную массы смеси: R=R0/µ, или через индивидуальные газовые постоянные компонентов и их массовые доли: 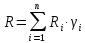 .В заключение выпишем все полезные для решения задач соотношения. Термическое уравнение состояния идеального газа: 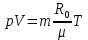,  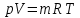,  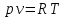;индивидуальная газовая постоянная: 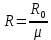,  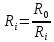;массовая доля компонента: 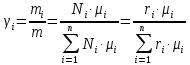;мольная и объёмная доли компонента: ; закон Дальтона: или 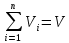; .молярная масса смеси: 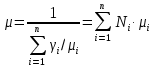 . Газовая постоянная смеси:  . . |
