Комбинаторика. История возникновения. Комбинаторика. История развития комбинаторики
 Скачать 0.79 Mb.
|
|
Оглавление
Введение В практической деятельности человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. С комбинаторными вычислениями приходится иметь дело представителям многих специальностей: прорабу при распределении между рабочими различных видов работ, диспетчеру при составлении графика движения. Завуч школы, составляя расписание учебных занятий, использует разные комбинации, шахматист из различных комбинаций выбирает наилучшую и т.д. Современная жизнь делает задачи на комбинаторные вычисления актуальными, так как появление компьютеров резко увеличило возможности комбинаторики и расширило сферу ее применения. Прикладное значение этой темы очень велико и затрагивает финансовую, демографическую, экологическую, социологическую и другие стороны нашей жизни. Интерес к теме возник, когда я участвовала в олимпиаде по математике, и там встречались следующие задачи: Задача 1. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько, туристов не владеют ни одним языком? Задача 2. Бег с препятствиями  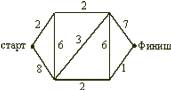 На дорожках стадиона расставлены барьеры (число барьеров на каждой дорожке указано на рисунке). Кенгуру хочет пробежать от старта до финиша, перепрыгивая через наименьшее возможное число барьеров. Сколько раз Кенгуру придется перепрыгнуть через барьеры? (A)11; (B) 8; (C) 10; (D) 18; (E) 6; После олимпиады, я задал учителю математики вопрос: «Как можно удобным способом решить задачи такого типа?» И, после этого узнал, что есть раздел математики - «Комбинаторика». Зная комбинаторику, мы сможем найти ответы на многие интересные вопросы: сколько существует трёхзначных чисел, сколькими способами в футбольной команде можно выбрать капитана и его заместителя, сколькими способами 8 человек могут встать в очередь к театральной кассе, сколько существует семи значных чисел, не содержащих цифры 5 и, наконец, какова вероятность выиграть в русское лото. Очень интересно! Неужели и я - смогу это понять? Так появился этот проект. Желание ответить на эти вопросы и определило цель моего проекта. Цель проекта: научиться решать задачи из раздела «комбинаторика». Для достижения цели были поставлены следующие задачи: Изучить исторический и теоретический материал о комбинаторике. Систематизировать задачи на комбинаторику по типам решения. Выяснить, какие задачи в жизни приходится решать людям. При работе над проектом применялись следующие теоретические методы: -изучение и анализ источников информации по комбинаторике и занимательной математике; - моделирование приемов использования комбинаторики в задачах. Понятие комбинаторика. В обыденной жизни нам нередко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи, требующие такого решения, называются комбинаторными. Область математики, в которой изучают комбинаторные задачи, называется комбинаторикой. В Энциклопедическом словаре юного математика дано определение: «Комбинаторика — это раздел математики, в котором изучают, сколько комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов»[1]. Комбинаторика нужна для изучения раздела математики «Теория вероятностей», который будет являться обязательным при изучении школьного курса математики. Способ рассуждений, которым пользуются при решении задачи, называют перебором возможных вариантов. 2. История развития комбинаторики С задачами, получившими название комбинаторных, оказывается, люди сталкивались в глубокой древности. Уже несколько тысячелетий назад в Древнем Китае увлеклись составлением магических квадратов, в которых заданные числа располагались так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же. В Древней Греции подсчитывали число различных комбинаций длинных и коротких слов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата и т.д. Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Первым рассматривал комбинаторику как самостоятельную ветвь науки всемирно известный немецкий учёный Готфрид Вильгельм Лейбниц. В 1666 году Лейбниц опубликовал «Рассуждения о комбинаторном искусстве». В своём сочинении Лейбниц, вводя специальные символы, термины , находит все k -сочетания из n элементов, выводит свойства сочетаний, строит таблицы сочетаний, после чего рассуждает о приложениях комбинаторики к логике, арифметике, к проблемам стихосложения и др. Мечтой Лейбница, оставшейся неосуществлённой, оставалось построение общей комбинаторной теории. В XVIII веке к решению комбинаторных задач обращались выдающиеся математики. Замечательные достижения в области комбинаторики принадлежат Леонарду Эйлеру. Он рассматривал задачи о разбиении чисел, о циклических расстановках, о построении магических и латинских квадратов. В 1713 году было опубликовано сочинение Я. Бернулли, в котором с достаточной полнотой были изложены известные к тому времени комбинаторные факты. Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей. Теперь комбинаторика находит приложения во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т.д. Комбинаторные задачи физики, химии, биологии, экономики и других наук, которые не поддавались ранее решению из-за трудоемкости вычислений, стали успешно решаться на ЭВМ. В результате этого комбинаторные методы исследования все глубже проникают во многие разделы науки и техники. В частности, с помощью ЭВМ решена проблема четырех красок: доказано, что любую карту можно раскрасить в четыре цвета так, чтобы никакие две страны, имеющие общую границу, не были окрашены в один и тот же цвет. Еще в 1844 году Дж. Сильвестр говорил: "Число, положение и комбинация - три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все математические идеи". 2.1. Дерево возможных вариантов. Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода - дерево возможных вариантов. Ветви дерева отображают различные события, которые могут иметь место. Корень дерева – состояние, в котором возникает необходимость выбора. Задача 1. Какие трехзначные числа можно составить из цифр 0, 2, 4? Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе. 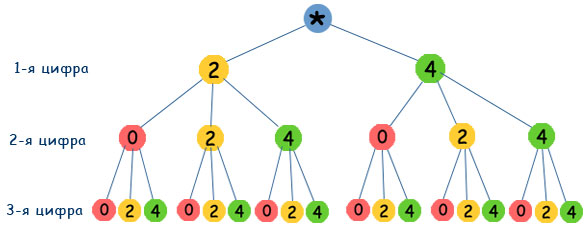 Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444. Задача 2. Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап - на байдарках, велосипедах или пешком. И третий этап пути - пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов? Решение. Построим дерево возможных вариантов, обозначив путешествие на поезде П, на автобусе - А, на байдарках - Б, велосипедах - В, пешком - Х, на канатной дороге - К. 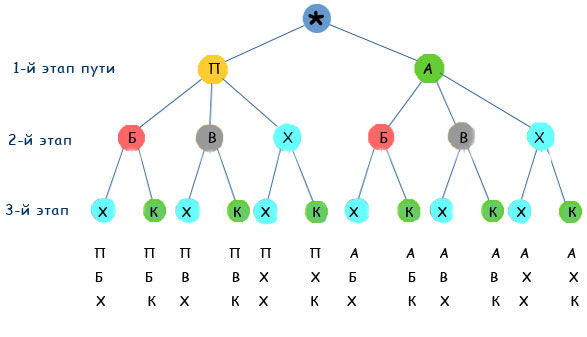 Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов. Задача 3. Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком. Решение. Построим дерево возможных вариантов, обозначив М - математика, Р - русский язык, И - история, А - английский язык, Ф - физкультура. 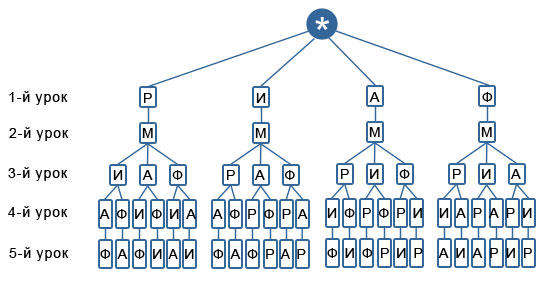 Ответ: Всего 24 возможных варианта. Задача 4. Саша ходит в школу в брюках или джинсах, к ним надевает рубашки серого, голубого, зеленого цвета или в клетку, а в качестве сменной обуви берет туфли или кроссовки. а) Сколько дней Саша сможет выглядеть по-новому? б) Сколько дней при этом он будет ходить в кроссовках? в) Сколько дней он будет ходить в рубашке в клетку и джинсах? Решение. Построим дерево возможных вариантов, обозначив Б - брюки, Д - джинсы, С - серая рубашка, Г - голубая рубашка, З - зеленая рубашка, Р - рубашка в клетку, Т - туфли, К - кроссовки. 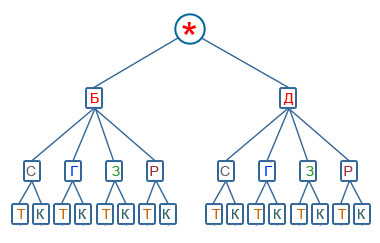 Ответ: а) 16 дней; б) 8 дней; в) 2 дня. 2.2. Перестановки. Простейшими комбинациями, которые можно составить из элементов конечного множества являются перестановки. Д  ва элемента a и b могут быть выписаны в строчку всего двумя способами: ab и ba. Для трёх элементов, существует 6 вариантов. Посчитаем и число перестановок для 4 элементов:1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312, 4321. Всего 24 перестановки, расположенные в 4 столбца по 6 перестановок в каждом. Для числа перестановок n элементов есть обозначение: n! (читаем: «эн факториал»). Факториал равен произведению всех натуральных чисел от n до 1. Например, 4! = 1 · 2 · 3 · 4= 24. Здорово! Одна строчка, а перебирая все возможные случаи выше, сколько записи всех перестановок. А если бы было не 4 элемента, а 8? Значит, и не надо было выписывать все возможные перестановки. Неужели так просто. Вот задачи, которые я смог решить. Задача 1. В семье – 6 человек, и за столом в кухне стоят 6 стульев. Семья решила каждый вечер, ужиная, рассаживаться на эти стулья по-новому. Сколько дней члены семьи смогут осуществлять задуманное? Решение. Ответ оказывается неожиданно большим: получается почти два года! Объясню его. Для удобства рассуждений , будем считать, что семья (бабушка, дедушка, мама, папа, дочь, сын) будет рассаживаться на стулья поочередно. Меня интересует, сколько всего существует различных способов их размещения на стульях. Предположим, что первой усаживается бабушка. У нее имеется 6 вариантов выбора стула. Вторым садится дедушка и независимо выбирает стул из 5оставшихся. Мама делает свой выбор третьей, и выбор у нее будет из 4 стульев. У папы будет уже три варианта, у дочки – 2, ну а сын сядет на единственный незанятый стул. По правилу умножения получаем, что имеется 720 различных способов размещения. Таким образом, в «игру с рассаживаниями» семья может играть 720 дней, т.е. почти два года. [3] Теперь стало понятно, что в обеих задачах речь шла о пяти перестановках. Задача 2. Из группы теннисистов, в которую входят четыре человека – Антонов, Григорьев, Сергеев и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары? Решение: Составим сначала все пары, в которые входит Антонов (для краткости будем писать первые буквы фамилий). Получим три пары: АГ, АС, АФ. Выпишем теперь пары, в которые входит Григорьев, но не входит Антонов. Таких пар две: ГС, ГФ. Далее составим пары, в которые входит Сергеев, но не входят Антонов и Григорьев. Такая пара только одна: СФ. Других вариантов составления пар нет, так как все пары, в которые входит Федоров, уже составлены. Итак, мы получили 6 пар: АГ, АС, АФ ГС, ГФ СФ, т.е. 3•2•1=6. значит, существует всего шесть вариантов выбора тренером пары теннисистов из группы. 2.3. Размещение Следующее важное понятие комбинаторики — размещение. Размещением называется расположение «предметов» (объектов) на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. Задача 1. В кафе предлагают два первых блюда: борщ, рассольник – и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из двух блюд, которые может заказать посетитель. Решение:
Ответ: 8 обедов. Задача 2. В классе, в котором 25 учеников, нужно выбрать командира, его заместителя и помощника заместителя. Сколькими способами это можно сделать? Решение: 25 способами можно выбрать любого ученика в командиры. Затем из 24 оставшихся — заместителя старосты. После этого любой из 23 оставшихся может оказаться помощником заместителя. Всего имеем: 25·24·23 = 13800 Ответ: 13800 способов. Задача 3.В футбольной команде (11 человек) нужно выбрать капитана и вратаря. Сколькими способами это можно сделать? Решение: 1. Капитаном может стать любой из 11 футболистов. 2. После выбора капитана на роль вратаря могут претендовать 10 оставшихся человек. Таким образом, есть 11 · 10 = 110 разных вариантов выбора. Ответ: 110 способов. Задача 4. Сколько семизначных чисел не содержат цифры 2? Решение: Всего цифр 10. Первую цифру не может быть нулем и двойкой, значит её можно выбрать 8 способами. Каждую следующую цифру можно выбрать 9 способами. 8 · 9 · 9 · 9 · 9 · 9 · 9 = 4 251 528. Ответ. 4 251 528 семизначных чисел. Вот это количество. А если бы не знать этот способ решения, перебрать все возможные случаи, кажется, невозможно. Это долго и опасно ошибиться. Задача 5. Сколькими способами можно составить расписание на день из 5 различных уроков, если изучается 14 предметов. Решение: В данном примере из 14 предметов нужно выбрать 5. Число способов составления расписания можно посчитать по формуле: 14 · 13 · 12 · 11 · 10 = 240240 Ответ: 240240 способов. Задача 6. Сколько времени потребуется, чтобы открыть дверь с кодовым замком, если на один набор чисел из 3-х цифр уходит 3 секунды. (Причем порядок нажатия кнопок с числами неважен). Решение: Первую цифру кода можно выбрать одной из 10 - всего 10 вариантов. Вторую цифру можно выбрать любой из 9 оставшихся. Значит, всего 10*9*8 = 720 комбинаций. Решение было бы верно, если бы не замечание в задаче: Причем порядок нажатия кнопок с числами неважен. Это означает, что композиция 123, 321, 213, и т.п. (всего их 6) одинаковые. Поэтому надо брать не размещение, а сочетания. Для сочетаний – результат нужно разделить на 6, т.е. на число перестановок из трёх элементов, равных 3!. 720 : 6=120 комбинаций, 120 · 3 = 360 секунд = 6 минут и код будет разгадан. Ответ: 6 минут. 3. Комбинаторика в различных областях жизнедеятельности человека. Области применения комбинаторики: учебные заведения (составление расписаний) сфера общественного питания (составление меню) лингвистика (рассмотрение вариантов комбинаций букв) география (раскраска карт) спортивные соревнования (расчёт количества игр между участниками) производство (распределение нескольких видов работ между рабочими) агротехника (размещение посевов на нескольких полях) азартные игры (подсчёт частоты выигрышей) химия (анализ возможных связей между химическими элементами) экономика (анализ вариантов купли-продажи акций) криптография (разработка методов шифрования) доставка почты (рассмотрение вариантов пересылки) биология (расшифровка кода ДНК) военное дело (расположение подразделений) астрология (анализ расположения планет и созвездий) 3.1 Комбинаторика в литературе. В басне Ивана Андреевича Крылова «Квартет»: «проказница Мартышка, Осёл, Козёл да косолапый Мишка» устроили любопытный эксперимент, они исследовали влияние взаимного расположения музыкантов на качество исполнения. Проказница-Мартышка, Осёл, Козёл, да косолапый Мишка Затеяли сыграть Квартет. Достали нот, баса, альта, две скрипки И сели на лужок под липки — пленять своим искусством свет. Ударили в смычки, дерут, а толку нет. «Стой, братцы, стой! — кричит Мартышка. — Погодите! Как музыке идти? Ведь вы не так сидите. Ты с басом, Мишенька, садись против альта, Я, прима, сяду против вторы; Тогда пойдёт уж музыка не та: у нас запляшут лес и горы!» Расселись, начали Квартет; Он всё-таки на лад нейдёт. «Постойте ж, я сыскал секрет, — Кричит Осёл: — мы, верно, уж поладим, коль рядом сядем». Послушались Осла: уселись чинно в ряд; А всё-таки Квартет нейдёт на лад. Вот пуще прежнего пошли у них разборы И споры, кому и как сидеть. Случилось Соловью на шум их прилететь. Тут с просьбой все к нему, чтоб их решить сомненье: «Пожалуй, — говорят: — возьми на час терпенье, Чтобы Квартет в порядок наш привесть: И ноты есть у нас, и инструменты есть; Скажи лишь, как нам сесть!» — «Чтоб музыкантом быть, так надобно уменье И уши ваших, понежней, — Им отвечает Соловей: — А вы, друзья, как ни садитесь, Всё в музыканты не годитесь». Мартышка, Осёл, Козёл и Мишка пересаживались, считая, что от этого зависит звучание музыки. И если бы не вмешался Соловей, участники квартета, наверное, перепробовали бы все возможные варианты. Так сколько же существует способов, чтобы рассадить, например в один ряд, четырех музыкантов? Число перестановок можно посчитать по формуле: 4 3 2 1 = 24 способа. Ответ: 24 способа. 3.2 Комбинаторика на шахматной доске и в играх. Шахматы не только популярная игра, но и источник множества интересных комбинаторных задач. Не случайно шахматные термины можно встретить в литературе по комбинаторике. Рассмотрим примеры задач на шахматной доске. Задача 1: Обойти конем все поля доски, посетив каждое из них по одному разу. Этой задачей занимались многие математики XVIII и XIX вв., в том числе и Л. Эйлер. Хотя задача была известна и до Эйлера, лишь он впервые обратил внимание на ее математическую сущность. Доказано, что таких маршрутов не более 30 млн. Задачи о маршрутах составлены и для других фигур. Задача 2: Сколькими способами можно расставить на доске восемь ферзей так, чтобы они не угрожали друг другу, т. е. никакие два из них не стояли бы на одной линии ( вертикали, горизонтали, диагонали). Доказано, что существует 92 требуемых расстановки. Подобные задачи ставятся для всех шахматных фигур. Исследование конкретных позиций или их классов в игре применяется для достижения определенных результатов, например матовой позиции за определенное число ходов. Так как борьба за уменьшение времени на «обдумывание» хода всей программой является принципиальным фактором, то математики затрачивают массу усилий на создание входящих в нее приложений (задач, решаемых при поиске нужного хода), работающих наиболее быстро, а также требующих по минимуму оперативной памяти. Это направление породило множество изящных логико-вычислительных проблем. Некоторые из них и по сей день предлагаются на различных математических и программистских олимпиадах, а также для развлечения на досуге. Выдающиеся шахматисты Клод Шеннон и Михаил Ботвинник внесли огромный вклад в создание математической модели шахматной игры и способствовали прогрессу в интеллектуализации программ для нее. Компьютерные шахматы — едва ли не самый убедительный пример за полвека развития информационных технологий, когда именно в интеллектуальной деятельности автомат успешно соперничает с человеком.  3.3 Комбинаторика и кубик Рубика. Необыкновенно популярной головоломкой стал кубик Рубика, изобретенный в 1975 году преподавателем архитектуры из Будапешта Эрне Рубиком для развития пространственного воображения у студентов. Кубик Рубика – это куб, как бы разрезанный на 27 одинаковых кубиков. В исходном положении каждая грань куба окрашена в один из 6 цветов. Остроумный механизм позволяет поворачивать любой слой из 9 кубиков, примыкающий к одной грани куба, вокруг ее центра. При этом цвета граней смешиваются. Задача состоит в том, чтобы вернуть разноцветные грани кубика в исходное положение. Теоретически из любого состояния кубика можно вернуться в исходное, не более чем за 23 хода. Лучшее время, показанное на чемпионате мира 1982 г. по скоростной сборке кубика Рубика, составило всего 22,95 секунды. Кубик Рубика служит не только развлечением, но и прекрасным наглядным пособием по комбинаторике.    3.4 Старинные задачи Задача: «Волк, козел и капуста» Крестьянину нужно перевезти через реку волка, козла и капусту. Лодка так мала, что в ней кроме крестьянина может поместиться только или волк, или козел, или капуста. Но если оставить волка с козлом, он его съест, а если оставить козла с капустой, то будет съедена капуста. Как быть крестьянину? Для решения требуется путем взаимной перестановки элементов расположить их в соответствии с условием задачи в определенном порядке. В случае с крестьянином переправу следует начать с перевозки козла. Затем крестьянин возвращается и берет волка, которого перевозит на другой берег и оставляет там, а козла возвращает назад на предыдущий берег. Оттуда забирает капусту и перевозит ее к волку. А затем возвращается и забирает козла. Задача-игра: «Крестики-нолики» Самая известная древняя игра. В квадрате, разделенном на девять клеток, игроки по очереди ставят в свободную клетку свой знак: крестик или нолик, стараясь выстроить три крестика или три нолика подряд. Тот, кто первым сделает это, тот и выигрывает. Если не делать ошибок, то игра оканчивается в ничью. Выиграть можно только в том случае, если противник ошибется. Самый правильный ход – занять угловую клетку. И если партнер не ответит на это своим знаком в центре, то он проиграл. Задача-игра: «Ним» Пусть имеется одна или несколько групп предметов. Играющие берут по очереди предметы из групп по правилам, которые заранее устанавливают: какое количество предметов разрешается брать за один раз и из скольких групп. Существует множество вариантов игры, и для большинства известна наилучшая стратегия, ведущая к выигрышу. Заключение В ходе проекта мною рассматривается история возникновения комбинаторики как науки, начиная с Древнего Китая и Древней Греции и заканчивая современным периодом ее развития. В работе приводятся сведения о великих математиках, которые стояли у истоков теории комбинаторных задач таких, как П. Ферма, Галилео Галилей, Я. Бернулли, Паскаль, Лейбниц, Л. Эйлер и многие другие. Таким образом, изложенные сведения, доказывают, что комбинаторные задачи сопровождают человечество на протяжении всей истории, переплетаясь с искусством и наукой, что математике присущ элемент игры, которая тренирует интеллект и развивает самые различные способности, особенно творческие. В рамках проекта полученная информация была изучена и применена при решении задач на перестановки, размещения, и были сделаны выводы, что несомненно, знание правил решения комбинаторных задач дает шанс намного быстрее прийти к положительному результату в логических рассуждениях. В ближайшем будущем я научусь решать более сложные задачи комбинаторики, а знания по этой теме будут востребованы при решении задач олимпиадного типа и помогут мне в будущем при подготовке к итоговой аттестации по математике. Вывод: Комбинаторика повсюду. Комбинаторика везде. Комбинаторика вокруг нас. Думаю, что цели я добился, так как после написания работы расширил и углубил свои знания по комбинаторике и научился решать задачи из этого раздела. Литература: 1.Энциклопедический словарь юного математика - /составитель Савинов А.П..- М.: Педагогика » -1985г.-352стр с ил. 2.Виленкин Н.Я. Комбинаторика.: Изд. « Наука»,1969г. 3.Деплан И. Я ., Виленкин Н.Я. За страницами учебника математики.- Пособие для учащихся 5-6кл средних школ. М.:Просвещение,1989-287стр. с иллюстрациями. 4.Г. Я. Гик «Занимательные математические игры». - М.:Знание,1982г. 5.Математическая энциклопедия /Виноградов И.М..-М.:Советская энциклопедия. Том 3.,1984г 6.Богомолов Н.В. Практические занятия по математике: Учеб. Пособие для техникумов. – 2-е изд., перераб.-М.: Высш. Школа, 1983.-399 с., ил. 7.Энциклопедия для детей. Т.11. Математика/Глав. Ред. М.Д. Аксенова.- М.: Аванта+, 2002.- 688с.: ил. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||