ЛАБ 1 Анненков. Итерационные методы решения систем линейных алгебраических уравнений
 Скачать 14.82 Kb.
|
Теория: Метод простых итераций Рассмотрим систему линейных алгебраических уравнений Аx̅ = b̅ Где А – матрица размерности n˟n, x̅ и b̅ - векторы размерности n. Метод состоит в том, что данная система преобразуется к виду x̅=Bx̅+c̅ и её решение вычисляется как предел последовательности x̅(k+1)=Bx̅(k)+c̅ где k = 0,1,... - номер очередного приближения к решению. Для сходимости итерационной последовательности к решению достаточно выполнение условия ||B||= 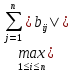 , то условие ||B|| < 1 равносильно условию диагонального преобладания исходной матрицы А. При выполнении достаточных условий сходимости начальное приближение x̅(0)Можно задать произвольно. Если решение ищется с точностью ε > 0, то итерационный процесс заканчивается, когда ||x̅(k+1) - x̅(k)||<ε, где ||x̅|| = 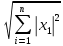 . |