методы решения линейных уравнений. Методы решения линейных уравнений коррекция. Методы решения систем линейных алгебраических уравнений
 Скачать 156.07 Kb. Скачать 156.07 Kb.
|
|
Содержание Вступление 2 Метод подстановки 2 Метод перебора коэффициентов (способ сложения) 3 Графический метод 3 Метод Гаусса 7 Метод Крамера 4 Заключение 13 Список литературы 14 Методы решения систем линейных алгебраических уравнений Решение систем линейных алгебраических уравнений, несомненно является важнейшей темой курса линейной алгебры. Огромное количество задач из всех разделов математики сводится к решению систем линейных уравнений. Этими факторами объясняется причина выбора данной темы. С помощью этой работы Вы сможете: подобрать оптимальный метод решения системы линейных уравнений; изучить теорию этого вопроса; решить систему линейных уравнений. Цель работы: изучить методы систем линейных уравнений, совершенствовать умение решать системы уравнений. Объект исследования: системы линейных алгебраических уравнений. В школьном курсе 7 класса мы изучили три основных способа решения элементарных систем: подстановки, сложения и графический. Определение: Если число уравнений системы равно числу неизвестных переменных и определитель основной матрицы не равен нулю, то систему называют элементарной. Такие системы уравнений имеют единственное решение. Рассмотрим решение систем этими способами. Метод подстановки Суть: Из какого-нибудь уравнения выразить одну неизвестную переменную и подставить её в оставшиеся уравнения, следом брали следующее уравнение, выражали следующую неизвестную переменную и так далее. Например:  Решить систему уравнений Решить систему уравнений Выразим пременную х через у из второго уравнения х=7 – 3у и подставим в первое. Получим уравнение  . Решая уравнение получим у = 1 и подставим в выражение для х. Решая полученное уравнение, х= 4. Система имеет единственное решение . Решая уравнение получим у = 1 и подставим в выражение для х. Решая полученное уравнение, х= 4. Система имеет единственное решение  . Преимущества способа его универсальность, недостатки трудоёмкость . Преимущества способа его универсальность, недостатки трудоёмкостьМетод перебора коэффициентов (Способ сложения). Цель: переберая коэффициентыи домнажая левую правую часть уравнения на число, получить противоположные коэффициенты при одноименной переменной. Почленно складывая уравнения исключить одну переменную. Например: решим систему (СМ. выше) методом сложения. Почленно складывая уравнения получим 3х=12, откуда х =4. Подставим в любое из уравнений и решив его получим у = 1. Ответ (4;1). Самый простой и наглядный способ это графический метод Суть: Построить графики уравнений и найти координаты точек пересечения. Недостаток –неточность, обязательна проверка корней. Рассмотрим ещё два основных способа решения систем уравнений Метод Гаусса и Метод Крамера. Решение систем линейных уравнений методом Крамера. Пусть нам требуется решить систему линейных алгебраических уравнений  в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, Пусть  При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как  . Так находится решение системы линейных алгебраических уравнений методом Крамера. . Так находится решение системы линейных алгебраических уравнений методом Крамера.Например: Решите систему линейных уравнений методом Крамера  . . Решение. Основная матрица системы имеет вид  . Вычислим ее определитель (при необходимости смотрите статью определитель матрицы: определение, методы вычисления, примеры, решения): . Вычислим ее определитель (при необходимости смотрите статью определитель матрицы: определение, методы вычисления, примеры, решения): Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера. Составим и вычислим необходимые определители  Находим неизвестные переменные по формулам 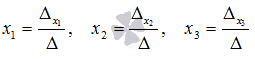 : :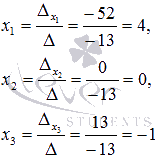 Ответ: x1 = 4, x2 = 0, x3 = -1. Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех. Решение систем линейных уравнений методом Гаусса. Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными  определитель основной матрицы которой отличен от нуля. Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x1 из всех уравнений системы, начиная со второго, далее исключается x2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная xn. Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находится xn, с помощью этого значения из предпоследнего уравнения вычисляется xn-1, и так далее, из первого уравнения находится x1. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса. Кратко опишем алгоритм исключения неизвестных переменных. Будем считать, что 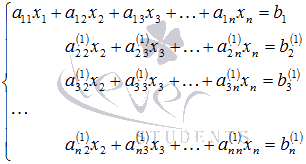 где  , а , а  . .К такому же результату мы бы пришли, если бы выразили x1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x1 исключена из всех уравнений, начиная со второго. Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке 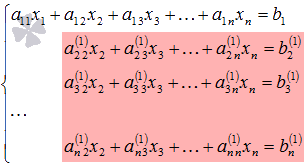 Будем считать, что Для этого к третьему уравнению системы прибавим второе, умноженное на 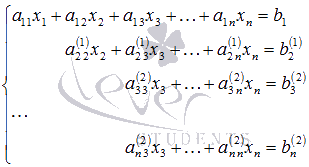 где 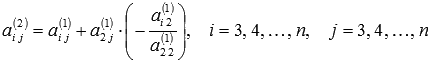 , а , а  . Таким образом, переменная x2 исключена из всех уравнений, начиная с третьего. . Таким образом, переменная x2 исключена из всех уравнений, начиная с третьего.Далее приступаем к исключению неизвестной x3, при этом действуем аналогично с отмеченной на рисунке частью системы  Так продолжаем прямой ход метода Гаусса пока система не примет вид 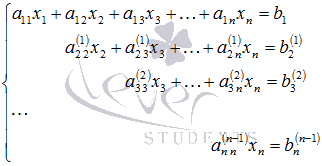 С этого момента начинаем обратный ход метода Гаусса: вычисляем xn из последнего уравнения как  , с помощью полученного значения xn находим xn-1 из предпоследнего уравнения, и так далее, находим x1 из первого уравнения. , с помощью полученного значения xn находим xn-1 из предпоследнего уравнения, и так далее, находим x1 из первого уравнения.Пример. Решите систему линейных уравнений  методом Гаусса. методом Гаусса. Решение. Исключим неизвестную переменную x1 из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на 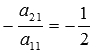 и на и на 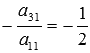 соответственно: соответственно: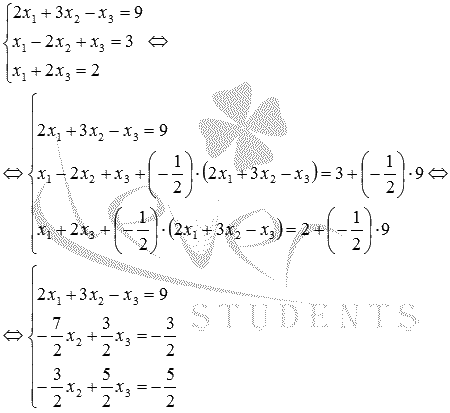 Теперь из третьего уравнения исключим x2, прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на  : :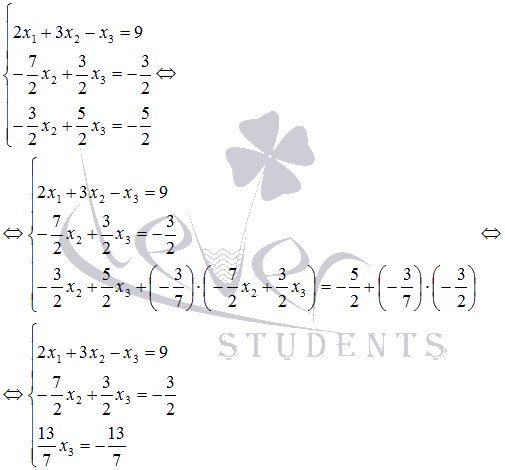 На этом прямой ход метода Гаусса закончен, начинаем обратный ход. Из последнего уравнения полученной системы уравнений находим x3: 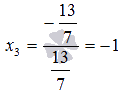 Из второго уравнения получаем 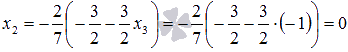 . . Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса Ответ: x1 = 4, x2 = 0, x3 = -1. Методом Гаусса можно решать системы линейных алгебраических уравнений любого вида без предварительного их исследования на совместность. Процесс последовательного исключения неизвестных переменных позволяет сделать вывод как о совместности, так и о несовместности СЛАУ, а в случае существования решения дает возможность отыскать его. Выводы: У каждого из приведённых способов есть свои недостатки и преимущества, выбор метода для решения системы линейных уравнений зависит от возможностей пользователя. Я выделила для себя самые простые способы - это метод сложения и метод Крамера. Список литературы 1) Аль-Хорезми Мухаммад Математические трактаты. Пер. Б. А. Розенфельда. – Ташкент.: Наука, 1994 – 132с. 2) Башмакова И. Г. Диофант и диофантовые уравнения. – М.: Наука, 1972 - 68с. 3) Бесчетнов В.М. Математика. Курс лекций для учащихся 7 - 11 классов. Т1.- М.: Демиург,1994 - 288с. 4) Гельфанд М.Б., Павлович В.С. Внеклассная работа по математике. - М: Просвещение, 1965 - 208с. 5) Глейзер Г.И.История математики в школе 9- 11 классы. - М: Просвещение, 1983 - 352с., ил., черви 6) Депман И. Рассказы о старой и новой алгебре. Л: детская литература , 1967 - 144с. 7) Егерев В.К. и другая Методика построения графиков функции. М: Высшая школа, 1970 - 152с. |
