Контрольная. Итоговое задание. Итоговое задание
 Скачать 89.99 Kb.
|
|
Итоговое задание 1. Рассчитайте точечный и интервальный прогноз урожайности сельскохозяйственной культуры на 9 год. Сделайте вывод об устойчивости тенденции изменения показателей временного ряда. Таблица 1 Динамика урожайности сельскохозяйственной культуры
Решение. Так как урожайность меняется по годам более-менее равномерно, то для всех рядов динамики урожайности зерновых культур формой тренда может служить уравнение прямой линии. 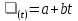 где,  - теоретические уровни;a - средняя урожайность; b - среднегодовой абсолютный прирост; t - обозначение времени.   Теперь составим точечный и интервальный прогноз сельскохозяйственной культуры на 9 год. Обозначение времени t = 9.  ц/гаСреднее квадратическое отклонение:  Коэффициент колеблемости:  Интервальный прогноз рассчитывают с учетом ежегодной колеблемости урожайности. Зная коэффициент колеблемости, рассчитаем среднее квадратическое отклонение для 9 года по формуле: 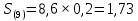 ц/гаВ 9 году прогноз урожайности сельскохозяйственной культуры будет в пределах  ц/га2. Получены данные о динамике спроса в течение 12 месяцев (усл. ед.). Таблица 2 Динамика спроса
Определить вид прогнозной функции, рассчитать параметры методом наименьших квадратов. Дать прогноз уровня спроса на I месяц следующего года, определив возможность его случайного отклонения. Оценить степень устойчивости тенденции. Решение. Параметры a и b линейной зависимости  (обозначим спрос за y) по методу наименьших квадратов можно найти из системы уравнений: где суммирование ведется по i от 1 до 12. Составим расчетную таблицу:
Получаем систему: 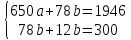 откуда находим a = 0,69 , b = 0,07 , то есть получаем функцию  .Определим ожидаемый спрос на I месяц следующего года:  Построим точки и линию на одной диаграмме: 3.Имеются поквартальные данные о прибыли компании за четыре года (табл. 3). Таблица 3 Прибыль компании, тыс. долл.
 Рис. 1 Динамика прибыли предприятия График временного ряда (рис. 1) свидетельствует о наличии сезонных колебаний (период колебаний равен 4) и общей убывающей тенденции уровней ряда. Прибыль компании в весенне-летний период выше, чем в осенне-зимний период. Поскольку амплитуда сезонных колебаний уменьшается, можно предположить существование мультипликативной модели. Определите ее компоненты и получите прогнозные значения прибыли на первое полугодие пятого года. Решение.
|