Осложнения при бурении. Осьмушкин Сырчина. Изменение рейсовой скорости бурения
 Скачать 63.9 Kb. Скачать 63.9 Kb.
|
 Министерство науки и ВЫСШЕГО образования Российской Федерации ФГБОУ ВО «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ имени Серго Орджоникидзе» (МГРИ) ________________________________________________________________________ ФАКУЛЬТЕТ ТЕХНОЛОГИИ РАЗВЕДКИ И РАЗРАБОТКИ КАФЕДРА СОВРЕМЕННЫХ ТЕХНОЛОГИЙ БУРЕНИЯ СКВАЖИН ВАРИАНТ № 9 по предмету «Оптимизация буровых работ и планирование эксперимента» на тему: «Изменение рейсовой скорости бурения» Выполнил: ст. группы ЗНД-18к Осьмушкин А.В. Проверил: преп. Сырчина А.С. МОСКВА, 2023 г. Определение основных статистических оценок выборки Таблица 1. Исходные данные
Определение среднего значения случайной величины: Среднее значение 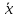 – это среднее арифметическое из всех измеренных значений: – это среднее арифметическое из всех измеренных значений: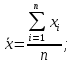 где n – количество наблюдений, 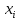 – значения случайной величины. – значения случайной величины.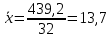 Определение меры разброса случайной величины – дисперсии: Дисперсией D случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания. Дисперсия вычисляется по формуле: 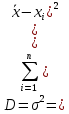 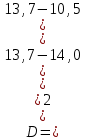 Определение среднеквадратического отклонения: Среднеквадратическое отклонение 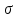 – это число, равное квадратному корню из дисперсии: – это число, равное квадратному корню из дисперсии: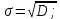 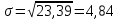 Отбраковка грубых ошибок Среди результатов выборки иногда присутствуют наблюдения, сильно отличающиеся от остальных. Такое расхождение может возникнуть вследствие изменения условий бурения, больших погрешностей при замерах параметров процесса, свойств пород и т.д. При обработке статистического материала необходимо убедиться, что в выборке отсутствуют грубые ошибки, которые называются «выскакивающими значениями». Грубые ошибки необходимо отбраковать. Для отбраковки используем два метода: метод Шовене и правило «трех сигм». Отбраковка по критерию Шовене При отбраковке по критерию Шовене значение случайной величины должно находиться в интервале: 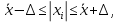 где 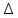 - критерий Шовене, который находится по формуле: - критерий Шовене, который находится по формуле: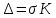 , ,где К – табличный коэффициент. При количестве измерений n==32 он равен 2,42 Производим отбраковку непредставительных данных: Отбраковка производится по критерию Шовене: 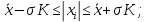 где: К – критерий Шовене (К=2,42) 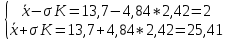 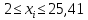 Отбраковка по правилу «трех сигм» Второй метод отбраковки грубых ошибок, использованный в работе, - метод отбраковки по правилу «трех сигм», согласно которому все измерения, не лежащие в интервале 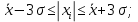 должны отбрасываться как маловероятные. При вычислении был получен следующий интервал: 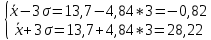 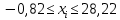 1.4 Отбраковка «выскакивающих значений» После отбраковки имеем случайные величины: Таблица 2. Данные после отбраковки
Производим пересчет значений: 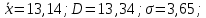 Рассчитаем коэффициент вариации: 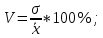 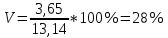 Интервальная оценка параметра выборки Интервальная оценка основана на определении некоторого интервала, внутри которого с определенной вероятностью находится истинное значение средней величины. Вероятность того, что действительное значение измеряемой величины лежит в пределах ( 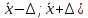 и представляет собой доверительную вероятность: и представляет собой доверительную вероятность: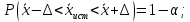 где 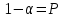 - доверительная вероятность, - доверительная вероятность, 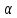 - уровень значимости. - уровень значимости.Доверительный интервал определяет диапазон, в котором находится истинное значение средней величины: 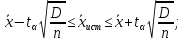 где: D – дисперсия, 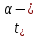 критерий Стьюдента ( зависит от принятой вероятности – Р или от уровня значимости – критерий Стьюдента ( зависит от принятой вероятности – Р или от уровня значимости – 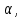 а также количества степеней свободы). В наших расчетах: а также количества степеней свободы). В наших расчетах: 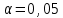 или Р = 0,95=95%, а критерий Стьюдента, согласно табличным значениям примем равным или Р = 0,95=95%, а критерий Стьюдента, согласно табличным значениям примем равным 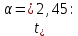 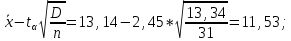 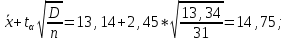 Таким образом, неравенство (11,53<13,14<14,75) является верным, следовательно, с вероятностью 95% средняя величина найдена правильно. 1.6 Необходимое и достаточное количество экспериментов Минимальное необходимое количество опытов: 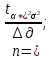 где: 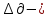 допустимое с точки зрения исследователя отклонение значение случайной величины от среднего. В нашем случае допустимое отклонение примем равным: допустимое с точки зрения исследователя отклонение значение случайной величины от среднего. В нашем случае допустимое отклонение примем равным: 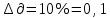 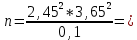 799,68 799,68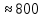 Группировка данных Для расчета статистических характеристик будем применять компактный метод расчета с предварительной группировкой данных. Для этого весь диапазон исходных значений от 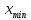 до до 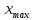 разбивается на равные интервалы, границы которых удобно брать округленными. разбивается на равные интервалы, границы которых удобно брать округленными.- Определяем размах ряда: 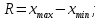 где 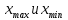 - максимальное и минимальное значение случайных величин соответственно. - максимальное и минимальное значение случайных величин соответственно.R = 32-3,7= 28,3; - Выбираем число интервалов разбиения k вариационного ряда. Число классов k определяется по правилу Штюргесса: 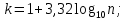 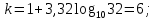 -Далее определяется длина интервалов разбиения (интервал шага): 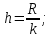 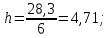 Число значений в классе называют частотой. Если выразить частоту в относительных долях к общему числу значений, то получим частость. В таблице 3 представлены интервалы, их границы, частность и частота их встречи в данной выборке. Таблица 3. Интервальный вариационный ряд
Данные таблицы 3 позволяют построить гистограмму значений случайной величины (рис.1). Гистограмма – статистическая фигура, состоящая из прямоугольников с основанием в виде отрезков, соответствующие длинам интервалов и высотам, соответствующим частостям. Для построения гистограммы по оси абсцисс откладываются интервалы, по оси ординат – частоты в виде ступенек. Для построения полигона рассеивания в серединах классов откладываются ординаты, пропорциональные абсолютным частотам. Вершины ординат соединяют линиями. 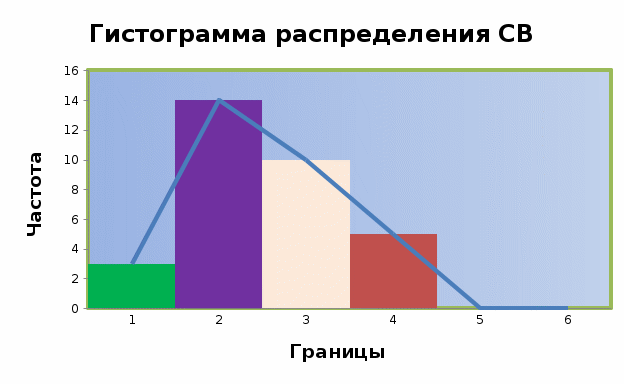 Рисунок 1. Гистограмма распределения случайной величины Вывод В процессе выполнения данной расчетно-графической работы были определены основные статистические оценки выборки, при анализе выборки была найдена дисперсия и среднеквадратичное отклонение. При обработке статистического материала я выявил наличие «выскакивающих значений» или грубых ошибок. Данные ошибки я выявил при помощи метода Шовене и правила «трёх сигм». После отбраковки грубых ошибок мною был произведен пересчет значений и составлена новая таблица с данными. Далее была произведена группировка данных, определен размах ряда, длина и число интервалов на основе этих данных составлена гистограмма и полигон. Данный график наглядно показал и подтвердил точность выше произведенных расчетов. Оценка значимости различия средних значений двух выборок. В таблице представлены значения случайных величин первой и второй выборки:
Оценка значимости различия средних значений двух выборок с использованием критерия Стьюдента При обработке результатов наблюдений часто возникает необходимость в проверке гипотез относительно средних значений 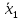 и и 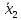 двух независимых выборок двух независимых выборок 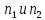 . При этом применяется выборочная статистика. . При этом применяется выборочная статистика.- Вычисляются средние значения выборок по формуле: 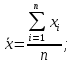 Для первой выборки: 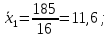 Для второй выборки:  - Вычисляются дисперсии выборок: 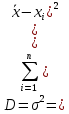 Для первой выборки: 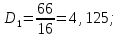 Для второй выборки: 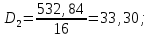 Когда обе дисперсии неизвестны и не предполагается, что они равны, то есть 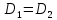 равенство двух средних проверяют с помощью приближенного экспериментального коэффициента Стьюдента: равенство двух средних проверяют с помощью приближенного экспериментального коэффициента Стьюдента: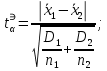 где 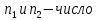 наблюдений для первого и для второго опыта соответственно. наблюдений для первого и для второго опыта соответственно.- Расчетное значение критерия Стьюдента: 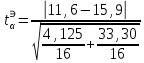 =1,84 =1,84Табличное значение критерия Стьюдента при 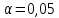 , а число степеней свободы , а число степеней свободы 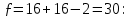 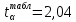 Так как 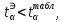 то различие средних значений существенно, а значит, выборки не относятся к одной генеральной совокупности. то различие средних значений существенно, а значит, выборки не относятся к одной генеральной совокупности.2.3 Оценка значимости различия средних значений двух выборок с использованием критерия Фишера. Распределение Фишера, называемое также Ф-распределением, для проверки гипотезы о равенстве дисперсий случайных величин. В качестве критерия Фишера 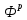 служит отношение дисперсий, причем в числитель отношения всегда помещают большую дисперсию. служит отношение дисперсий, причем в числитель отношения всегда помещают большую дисперсию.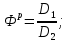 - Рассчитываем экспериментальное значение критерия Фишера: 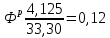 - Вычисленное значение критерия сравнивается с табличным значением. Табличное значение критерия Фишера при 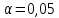 и и 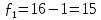 и и  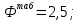 Так как 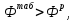 то расхождение дисперсий велико и различие средних значений существенно. то расхождение дисперсий велико и различие средних значений существенно.- Вычисляется средневзвешенная дисперсия: 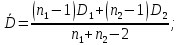 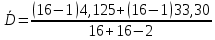 =18,71 =18,71- Табличное значение критерия Стьюдента при при 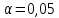 , и , и 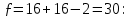 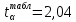 - Выполняется проверка условия: 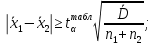 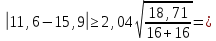 1,56 1,564,3 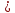 1,56 1,56Так как условие выполняется, расхождение дисперсий велико и различие средних значений существенно. Вывод: Из табличных значений случайных величин первой и второй выборки была произведена оценка значимости различия средних значений двух выборок с использованием критерия Стьюдента и Фишера. Была выполнена проверка, которая соответствовала условию. Таким образом расхождение дисперсий велико и различие средних значений существенно. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 /
/