Лабораторная работа №3 Тема: «Измерение информации»
Цель работы: познакомиться с основными подходами к измерению информации и использовать их при решении задач.
Порядок выполнения работы
1. Познакомиться с системой единиц измерения количества информации.
2. Рассмотреть содержательный и алфавитный подходы к измерению информации.
3. Закрепить полученные навыки при решении задач.
-
Минимальную порцию информации о каком-либо свойстве объекта принято называть битом (binary digit – двоичная цифра). Бит – единица измерения информации, представляющая собой выбор из двух равновозможных вариантов. Бит представляет собой обозначение одного двоичного разряда, способного, в зависимости от сделанного выбора, принимать значение 1 или 0.
Таблица степеней двойки показывает, сколько комбинаций можно закодировать с помощью некоторого количествабит:
Количество бит
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Количество комбинаций
|
2
|
4
|
8
|
16
|
32
|
64
|
128
|
256
|
512
|
1024
|
Байт – единица измерения информации, представляющая собой последовательность, состоящую из 8 бит: 1 байт = 23 бит = 8 бит.
Каждый бит имеет определенное место внутри байта, которое называется разрядом. Разряды принято нумеровать справа налево. Например, третий бит в байте на самом деле находится в пятом разряде байта.
Для измерения больших объемов информации принято использовать производные единицы измерения, представленные в таблице:
Название
|
Степень
|
Условное обозначение
|
Килобайт
|
210 (1024 байт)
|
Кбайт, KB
|
Мегабайт
|
220 (1024 Кбайт)
|
Мбайт, MB
|
Гигабайт
|
230(1024 Мбайт)
|
Гбайт, GB
|
Терабайт
|
240 (1024 Гбайт)
|
Тбайт, TB
|
Петабайт
|
250 (1024 Тбайт)
|
Пбайт, PB
|
Эксабайт
|
260 (1024 Пбайт)
|
Эбайт, EB
|
Зеттабайт
|
270 (1024 Эбайт)
|
Збайт, ZB
|
Йоттабайт
|
280 (1024 Збайт)
|
Йбайт, YB
|
Задание №1
Заполнить пропуски значениями, в соответствии с предложенными единицами измерения:
Вариант
|
Условие
|
1
|
5 Гбайт = ? Кбайт = ? бит;
512 Кбайт = 2? байт = 2? бит;
384 Мбайт = (2? + 2?) байт = (2? + 2?) бит.
|
2
|
? Гбайт = ? Кбайт = 12288 бит;
8 Пбайт = 2? Гбайт = 2? Кбайт;
768 Тбайт = (2? + 2?) Мбайт = (2? + 2?) бит.
|
3
|
? Гбайт = 7168 Мбайт =? Кбайт;
256 Кбайт = 2? байт = 2? бит;
192 Тбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
4
|
? Гбайт = ? Мбайт = 2500 байт;
512 Гбайт = 2? Кбайт = 2? бит;
160 Тбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
5
|
? Тбайт = ? Мбайт = 700 000 000 бит;
0,5 Тбайт = 2? Кбайт = 2? бит;
288 Тбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
6
|
2 Гбайт = ? Кбайт = ? бит;
256 Мбайт = 2? Кбайт = 2? бит;
576 Тбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
7
|
5,5 Мбайт = ? Кбайт = ? бит;
1,5 Кбайт = 2? байт = 2? бит;
528 Гбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
8
|
? Кбайт = ? байт = 10 073 741 бит;
2,5 Мбайт = 2? Кбайт = 2? байт;
320 Гбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
9
|
? Гбайт = 15 Мбайт = ? бит;
3,5 Мбайт = 2? байт = 2? бит;
96 Гбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
10
|
? Тбайт = ? Мбайт = 1 073 741 824 байт;
512 Гбайт = 2? Мбайт = 2? Кбайт;
80 Гбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
11
|
? Кбайт = ? байт = 1024 бит;
1024 Тбайт = 2? Мбайт = 2? Кбайт;
144 Гбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
12
|
1,5 Гбайт = ? Мбайт = ? бит;
0,5 Гбайт = 2? Кбайт = 2? байт;
544 Гбайт = (2? + 2?) Кбайт = (2? + 2?) бит.
|
-
Новые сведения о свойствах объектов окружающего нас мира содержат информацию для человека и, следовательно, пополняют его знания. При содержательном подходе возможна качественная оценка полученной информации, например, насколько она для нас полезна, важна или наоборот – вредна.
Неопределенность знания о некотором событии – это количество возможных результатов события (бросания монеты, кубика; вытаскивания жребия и пр.). Уменьшение неопределенности знания человека в 2 раза, несет для него 1 бит информации.
Количество информации (I) для событий с различными вероятностями определяется по формуле К.Шеннона:
где N – количество возможных событий; 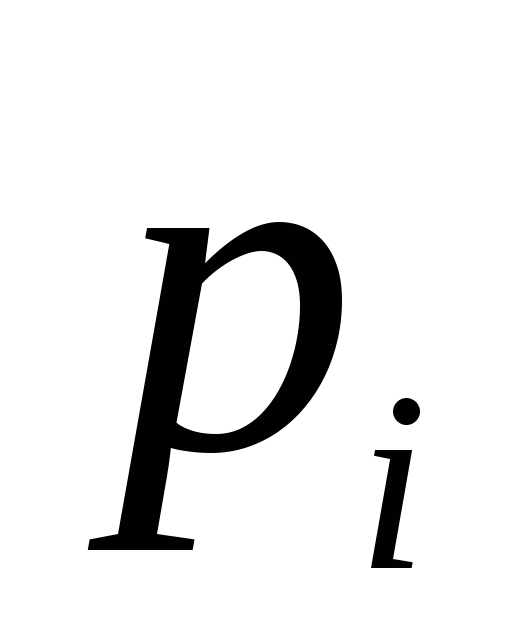 – вероятности отдельных событий. – вероятности отдельных событий.
Заметим, что сумма вероятностей равна 1.
Если события равновероятны, то количество информации (I) определяется по формуле Р.Хартли:
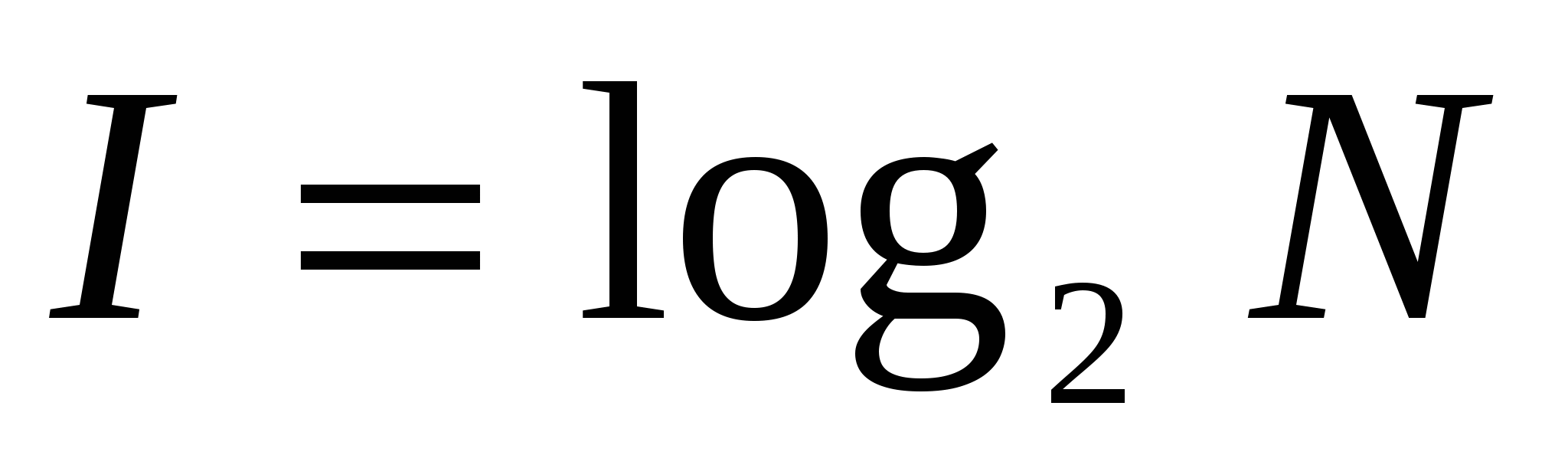 или или 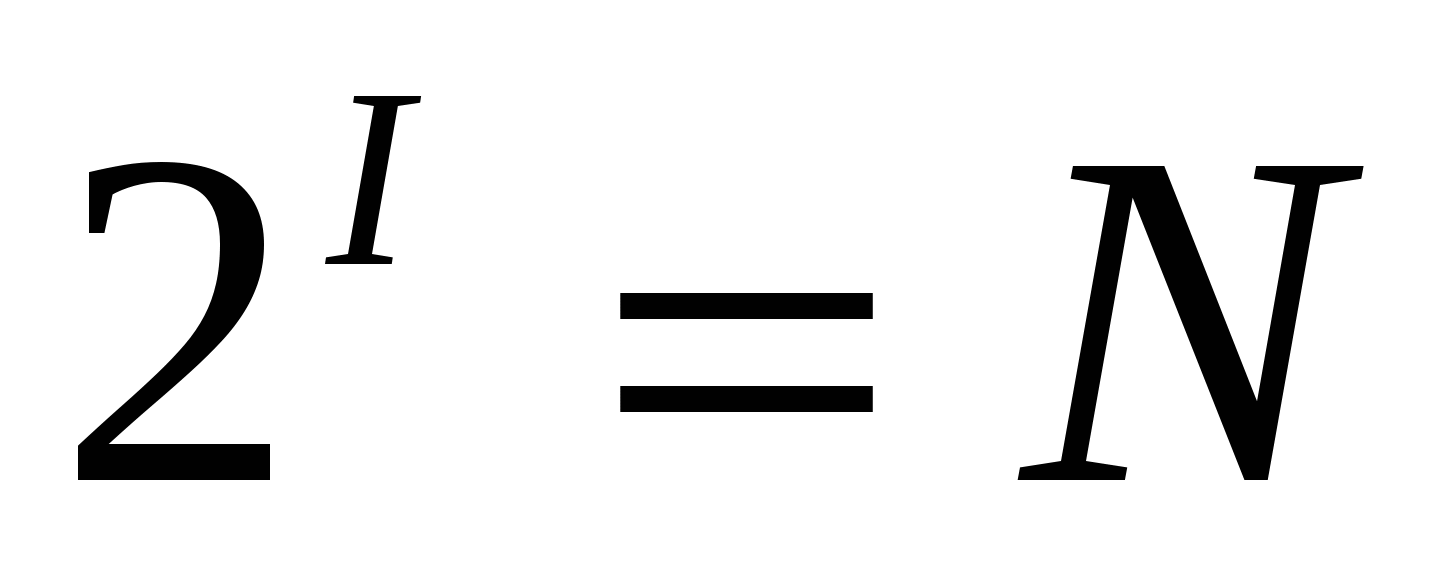
|
где N – количество равновероятных событий.
Алфавитный подход к измерению количества информации
Алфавит – множество символов, используемых при записи текста. Полное количество символов в алфавите называется размером (мощностью) алфавита.
Алфавитный подход позволяет определить количество информации в тексте. Данный подход является объективным, т.е. он не зависит от человека, воспринимающего текст.
Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то мощность (N) алфавита вычисляется по формуле:
где i – информационный вес одного символа в используемом алфавите.
Если весь текст состоит из К символов, то при алфавитном подходе размер содержащейся в нем информации равен:
Задание №2
Вариант
|
Условие
|
1
|
Какое количество информации несет в себе сообщение о том, что нужный вам файл находится на одном из восьми дисков?
|
2
|
В рулетке общее количество лунок равно 128. Какое количество информации вы получите в сообщении об остановке шарика в одной из лунок.
|
3
|
Какое количество информации получит второй игрок при игре в крестики-нолики на поле 8х8 после первого хода первого игрока, играющего «крестиками»?
|
4
|
Сообщение о том, что ваш друг живет на десятом этаже, несет в себе 4 бита информации. Сколько может быть этажей в доме?
|
5
|
Какое количество информации получит второй игрок при игре в крестики-нолики на поле 4х4 после первого хода первого игрока?
|
6
|
При угадывании целого числа в некотором диапазоне было получено 6 бит информации. Сколько чисел содержит данный диапазон?
|
7
|
Сообщение о том, что Петя живет во втором подъезде, несет 3 бита информации. Сколько подъездов в доме?
|
8
|
Группа студентов пришла в бассейн, в котором 4 дорожки для плавания. Инструктор сообщил, что группа будет плавать на дорожке №3. Сколько информации получили студенты из этого сообщения?
|
9
|
В корзине лежат 8 шаров разного цвета. Сколько информации несет сообщение о том, что из корзины достали зеленый шар?
|
10
|
Было получено сообщение «Встречайте! Вагон №7». Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?
|
11
|
Сообщение о том, что ваш друг живет на десятом этаже несет в себе 5 бит информации. Сколько может быть этажей в доме?
|
12
|
При угадывании целого числа в некотором диапазоне было получено 7 бит информации. Сколько чисел содержит данный диапазон?
|
Задание №3
Вариант
|
Условие
|
1
|
Автомобильный номер длиной 6 символов составляется из заглавных букв (всего используется 12 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт. Определите объем памяти, необходимый для хранения 32 автомобильных номеров.
|
2
|
В базе данных хранятся записи, содержащие информацию о датах. Каждая запись содержит три поля: год (число от 1 до 2100), номер месяца (число от 1 до 12) и номер дня в месяце (число от 1 до 31). Каждое поле записывается отдельно от других полей с помощью минимально возможного числа бит. Определите минимальное количество бит, необходимых для кодирования одной записи.
|
3
|
Автомобильный номер длиной 10 символов составляется из заглавных букв (всего используется 21 буква) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт. Определите объем памяти, необходимый для хранения 81 автомобильного номера.
|
4
|
Для регистрации на сайте пользователю необходимо придумать пароль длиной ровно 15 символов. В пароле можно использовать десятичные цифры и 31 различных символов алфавита, причем все буквы используются в двух начертаниях – строчные и прописные. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый пароль – одинаковым и минимально возможным целым количеством байт. Определите объем памяти, необходимый для хранения 80 паролей.
|
5
|
Автомобильный номер длиной 5 символов составляют из заглавных букв (задействовано 30 различных букв) и любых десятичных цифр в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 50 номеров.
|
6
|
При регистрации в системе каждому пользователю выдаётся пароль, состоящий из 11 символов и содержащий только символы И, К, Л, М, Н. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 20 паролей.
|
7
|
При регистрации в системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы К, О, М, П, Ь, Ю, Т, Е, Р. Каждый такой пароль записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 30 паролей.
|
8
|
При регистрации в системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 12-буквенного набора А, В, Е, К, М, Н, О, Р, С, Т, У, X. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируются одинаковым и минимально возможным количеством бит. Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт. Определите объём памяти, необходимый для хранения сведений о 50 пользователях.
|
9
|
При регистрации в системе каждому пользователю выдаётся идентификатор, состоящий из 10 символов, первый и последний из которых – одна из 18 букв, а остальные – цифры (допускается использование 10 десятичных цифр). Каждый такой идентификатор в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование; все цифры кодируются одинаковым и минимально возможным количеством бит, все буквы также кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 25 паролей.
|
10
|
При регистрации в системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из набора И,Н,Ф, О, Р, М, А, Т, К. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи 25 паролей.
|
11
|
При регистрации в системе каждому пользователю выдаётся пароль, состоящий из 6 символов и содержащий только символы из 7-буквенного набора Н, О, Р, С, Т, У, Х. В базе данных для хранения сведений о каждом пользователе отведено одинаковое целое число байт, при этом для хранения сведений о 100 пользователях используется 1400 байт. Для каждого пользователя хранятся пароль и дополнительные сведения. Для хранения паролей используют посимвольное кодирование, все символы кодируются одинаковым и минимально возможным количеством бит. Сколько бит отведено для хранения дополнительных сведений о каждом пользователе?
|
12
|
При регистрации в системе, используемой при проведении командной олимпиады, каждому ученику выдается уникальный идентификатор – целое число от 1 до 1000. Для хранения каждого идентификатора используется одинаковое и минимально возможное количество бит. Идентификатор команды состоит из последовательно записанных идентификаторов учеников и 8 дополнительных бит. Для записи каждого идентификатора команды система использует одинаковое и минимально возможное количество байт. Во всех командах равное количество участников. Сколько участников в каждой команде, если для хранения идентификаторов 20 команд-участниц потребовалось 180 байт?
|
Задание №4
Вариант
|
Условие
|
1
|
Сообщение содержит 1536 символов. Его объем 3 Кбайт. Какова мощность алфавита?
|
2
|
Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 50 строк по 60 символов. Какой объем информации содержат 80 страниц текста?
|
3
|
Текст (использован 256-символьный алфавит), содержит 55 страниц; на каждой странице – 45 строк, в каждой строке – 62 символа. Каков объем информации в документе?
|
4
|
Какова мощность алфавита, с помощью которого записано сообщение, содержащее 1024 символов, если его объем составляет 1/512 Мбайта?
|
5
|
Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 65 строк по 55 символов. Какой объем информации содержат 110 страниц текста?
|
6
|
Сообщение содержит 768 символов. Его объем 1,5 Кбайт. Какова мощность алфавита?
|
7
|
Текст (использован 256-символьный алфавит), содержит 105 страниц; на каждой странице – 55 строк, в каждой строке – 40 символов. Каков объем информации в документе?
|
8
|
Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1/512 Мбайта?
|
9
|
Текст (использован 256-символьный алфавит), содержит 120 страниц; на каждой странице – 60 строк, в каждой строке – 55 символа. Каков объем информации в документе?
|
10
|
Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1/256 Мбайта?
|
11
|
Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 50 строк по 60 символов. Какой объем информации содержат 200 страниц текста?
|
12
|
Текст (использован 256-символьный алфавит), содержит 130 страниц; на каждой странице – 70 строк, в каждой строке – 55 символа. Каков объем информации в документе?
|
Задание №5
Вариант
|
Условие
|
1
|
По каналу связи передается пять сообщений, вероятность получения первого сообщения составляет 0,3; второго – 0,2; третьего – 0,14, а вероятности получения четвертого и пятого сообщений равны между собой. Какую степень неопределенности (энтропия) содержит событие после приема одного из сообщений?
|
2
|
Какую степень неопределенности (энтропия) содержит опыт после реализации одного из шести событий. Вероятность первого события составляет 0,15; второго – 0,25; третьего – 0,2; четвертого – 0,12; пятого – 0,12; шестого – 0,1.
|
3
|
В урне имеется 16 шаров, из них один шар красного цвета с зеленой полосочкой, три шара красного цвета и двенадцать шаров зеленого цвета. Какую степень неопределенности (энтропия) содержит сообщение о том, что из урны достали случайным образом шар красного цвета с зеленой полосочкой?
|
4
|
Вероятность первого события составляет 0,5, а второго и третьего-0,25. Какое количество информации можно получить после реализации одного из них?
|
5
|
В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?
|
6
|
В группе 8 студентов из 26 получили в сессию оценку «неудовл.», а в другой – 11 из 29. В каком случае легче предсказать успеваемость студента?
|
7
|
В урне содержится один красный и два зеленых шара, а в другой - два красных и три зеленых. В каком случае угадывание цвета извлеченного из урны шара более предсказуемо?
|
8
|
Какую степень неопределенности (энтропия) содержит опыт после реализации одного из пяти событий. Вероятность первого события составляет 0,4; второго – 0,1; третьего – 0,2; вероятности четвертого и пятого событий – равны.
|
9
|
В урне содержится три красных и один зеленый шар, а в другой - два красных и пять зеленых. В каком случае угадывание цвета извлеченного из урны шара менее предсказуемо?
|
10
|
Какую степень неопределенности (энтропия) содержит опыт после реализации одного из четырех событий. Вероятность первого события составляет 0,2; второго – 0,3; вероятности третьего и четвертого событий – равны.
|
11
|
В группе 6 студентов из 24 получили в сессию оценку «отл.», а в другой – 9 из 27. В каком случае сложнее предсказать успеваемость студента?
|
12
|
Какую степень неопределенности (энтропия) содержит опыт после реализации одного из шести событий. Вероятность первого события составляет 0,25; второго – 0,1; третьего – 0,15; четвертого – 0,18, вероятности пятого и шестого событий – равны.
| Контрольные вопросы
Что понимается под битом информации?
Дайте определение единицы измерения информации байта.
Определите понятие разряда в байте.
Перечислите производные единицы информации.
Что такое мощность алфавита?
По какой формуле можно вычислить размер алфавита?
Какие существуют основные подходы к измерению информации?
Запишите формулу, связывающую между собой количество событий с различными вероятностями и количество информации.
ПРИЛОЖЕНИЕ А
ПРИМЕРЫ ЗАДАЧ (С РЕШЕНИЯМИ)
Пример 1. После экзамена по информатике объявляют оценки («5», «4», «3» или «2»). Какое количество информации будет нести сообщение об оценке студента А, который выучил лишь половину билетов, и сообщение об оценке учащегося Б, который выучил все билеты.
Решение. Опыт показывает, что для учащегося А все четыре оценки (события) равновероятны и тогда количество информации, которое несет сообщение об оценке, можно вычислить по формуле Хартли:
I = Iog 2 4 = 2 бита.
В результате наблюдений, для студента В наиболее вероятной оценкой является «5» (р1 = 1/2), вероятность оценки «4» в два раза меньше (р2= 1/4), а вероятности оценок «2» и «3» еще в два раза меньше (р3=p4=1/8). Так как данные события не являются равновероятными, для подсчета количества информации воспользуемся формулой Шеннона:
I=- (1/2·log2l/2+1/4·log2l/4+1/8·log2l/8+1/8·log2l/8)бит= 1,75 бит
(log2l/2=-1, log2l/4=-2, log2l/8=-3).
Ответ: 2 бита; 1,75 бит.
Пример 2. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение том, что выпал номер 17?
Решение. Поскольку вытаскивание любого из 32 шаров равновероятно, то количество информации об одном выпавшем номере находится из уравнения: 2I =32. Так как 32=25, то I=5 бит. (Ответ не зависит от того, какой именно выпал номер).
Ответ: 5 бит.
Пример 3. Для регистрации на сайте пользователю требуется придумать пароль. Длина пароля – ровно 11 символов. В качестве символов используются десятичные цифры и 12 различных букв алфавита, причём все буквы используются в двух начертаниях: как строчные, так и заглавные (регистр буквы имеет значение).
Под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов, при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов.
Определите объём памяти, который занимает хранение 60 паролей (пароль должен занимать ЦЕЛОЕ число байт).
Решение.
согласно условию, в пароле можно использовать 10 цифр (0...9) + 12 заглавных букв алфавита + 12 строчных букв, всего 10+12+12=34 символа;
для кодирования 34 символов нужно выделить 6 бит памяти (5 бит не хватает, они позволяют закодировать только 25=32 варианта);
для хранения всех 11 символов пароля нужно 11*6 = 66 бит;
поскольку пароль должен занимать целое число байт, берем ближайшее большее (точнее, не меньшее) значение, которое кратно 8: это 72= 9*8; то есть один пароль занимает 9 байт;
следовательно, 60 паролей занимают 9*60 = 540 байт.
Ответ: 540 байт.
Пример 4. В базе данных хранятся записи, содержащие информацию о студентах:
<Фамилия> – 16 символов: русские буквы (первая прописная, остальные строчные);
<Имя> – 12 символов: русские буквы (первая прописная, остальные строчные);
<Отчество> – 16 символов: русские буквы (первая прописная, остальные строчные);
<Год рождения> – числа от 1960 до 1997.
Каждое поле записывается с использованием минимально возможного количества бит. Определите минимальное (целое) количество байт, необходимое для кодирования одной записи, если буквы е и ё считаются совпадающими.
Решение.
итак, нужно определить минимально возможные размеры в битах для каждого из четырех полей и сложить их;
известно, что первые буквы имени, отчества и фамилии – всегда заглавные, поэтому можно хранить их в виде строчных и делать заглавными только при выводе на экран;
таким образом, для символьных полей достаточно использовать алфавит из 32 символов (русские строчные буквы, «е» и «ё» совпадают, пробелы не нужны);
для кодирования каждого символа 32-символьного алфавита нужно 5 бит (32=25), поэтому для хранения имени, отчества и фамилии нужно
(16+12+16)*5=220 бит;
для года рождения есть 38 вариантов, поэтому для него нужно отвести 6 бит
(26 =64≥38);
таким образом, всего требуется 226 бита или 29 байт.
Ответ: 29 байт.
Пример 5. Текст содержит 150 страниц; на каждой странице – 40 строк, в каждой строке – 60 символов (для записи текста использовался 256-символьный алфавит). Каков объем информации в Мбайтах содержится в документе?
Решение. Мощность алфавита равна 256 символов, поэтому один символ несет 1 байт информации. Значит, страница содержит 40·60 = 2400 байт информации. Объем всей информации в документе (в разных единицах):
2400·150 = 360 000 байт.
360000/1024 = 351,6 Кбайт.
351,5625/1024 = 0,3 Мбайт.
Ответ: 0,3 Мбайт.
Пример 6. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов (страница текста), если его объем составляет 1,25 Кбайта?
Решение. Переведем информационное сообщение в биты:
1,25*1024*8=10240 бит.
Определим количество бит на один символ:
10240:2048=5 бит.
По формуле для мощности алфавита определим количество символов в алфавите:
N=2i=25=32 символа.
Ответ: 32 символа. |
 Скачать 158.5 Kb.
Скачать 158.5 Kb.