Измерение параметров электромагнитного контура
 Скачать 282.5 Kb. Скачать 282.5 Kb.
|
 Министерство образования Российской Федерации Санкт-Петербургский государственный горный институт им. Г.В. Плеханова (технический университет)  Отчёт по лабораторной работе № 4.По дисциплине: Общая и техническая физика(наименование учебной дисциплины согласно учебному плану) Тема: Измерение параметров электромагнитного контураВыполнил: студент гр. РТ-07 ______________ /Глухов А.В./ (подпись) (Ф.И.О.) ОЦЕНКА: _____________ Дата: __________________ ПРОВЕРИЛ:Преподаватель: ______ ____________ /Колосько А.Г./(должность) (подпись) (Ф.И.О.) Санкт-Петербург 2008 год. Цель работы: Экспериментальное определение индуктивности и добротности электромагнитного контура. Индуктивностьконтура равна отношению собственного магнитного потока, созданного некоторым током , протекающим по контуру, к силе этого тока. Электроёмкость данного проводника это величина равная отношению заряда, сообщённого проводнику, к изменению потенциала, вызванному этим зарядом. Добро́тность — характеристика колебательной системы, определяющая остроту резонанса и показывающая, во сколько раз запасы энергии в реактивных элементах контура больше, чем потери энергии на активных. Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии в течение каждого периода. Колебания в системе с высокой добротностью затухают медленно. Резонанс – явление возрастания амплитуды установившихся вынужденных колебаний до максимального значения при приближении частоты изменения внешней силы к частоте свобод. Свободные механические колебания всегда оказываются затухающими, т.е. колебаниями с убывающей амплитудой. Колебательный контур – электрическая цепь, в которой могут происходить колебания с частотой, определяемой параметрами самой цепи. Простейший колебательный контур содержит катушку индуктивности и конденсатор, соединенный последовательно или параллельно. Конденсатор – это система из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Диэлектриками или изоляторами называются такие тела, через которые электрические заряды не могут переходить от заряженного тела к незаряженному. Электрический заряд – физическая величина, определяющая электромагнитное взаимодействие. Амплитуда – модуль максимального смещения тела от положения равновесия. Вынужденные колебания – колебания, в цепи под действием внешней переодической электродвижущей силы. Частота колебаний – физическая величина обратная периоду колебаний. Период колебаний – минимальный интервал времени, через который происходит повторение движения тела. Свободные колебания – колебания в системе, которые возникают после выведения ее из положения равновесия. Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура. Индуктивность – это коэффициент пропорциональности L между силой тока I в контуре и магнитным потоком Ф, создаваемым этим током. Сила тока - отношение заряда, переносимого через поперечное сечение проводника за интервал времени, к этому интервалу времени. Магнитный поток – число силовых линий магнитного поля, пронизывающих замкнутый контур. Это величина равная произведению магнитной индукции В, площади S поверхности, ограниченную контуром, и косинусом угла между вектором магнитной индукции и нормалью к поверхности. Магнитное поле – особая форма материи, существующей независимо от нас, наших знаний о нем, обладающее свойствами отличающие его от других видов полей. Оно порождается электрическим током( движущимися зарядами), обнаруживается по действию на электрический ток. Магнитная индукция – физическая величина, равная отношению максимального значения модуля силы Ампера, действующей на проводник с током, к силе тока в проводнике и его длине. Сила Ампера – сила, с которой магнитное поле действует на проводник с током. Активным сопротивлением R называется физическая величина, определяемая отношение мощности Р переменного тока на участке электрической цепи к квадрату действующего значения силы тока I на участке. Электромагнитные колебания – это периодические или почти периодические изменения заряда, силы тока, напряжения. Мощность – отношение работы тока ко времени, за которое эта работа совершена. Работа тока – работа сил электрического поля, создающего электрический ток. Напряжение - отношение работы, совершаемой любым электрическим полем при перемещении положительного заряда из одной точки поля в другую, к значению заряда. В работе используется закон перехода энергии электрического поля в конденсаторе в энергию магнитного поля в катушке и обратно. Схема установки: Э 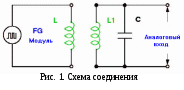 лектрический колебательный контур состоит из ёмкости С, индуктивности L1 и активного сопротивления R проводов (рис.1). При помощи функционального генератора (FG) напряжение прямоугольных импульсов низкой частоты подается на катушку возбуждения L. Для контура L1C имеются катушки различных длин l, диаметров 2rи числа витков N(соответствующие значения для номера каждой катушки представлены в таблице 2), емкость считается известной и установлена в разъёмник. лектрический колебательный контур состоит из ёмкости С, индуктивности L1 и активного сопротивления R проводов (рис.1). При помощи функционального генератора (FG) напряжение прямоугольных импульсов низкой частоты подается на катушку возбуждения L. Для контура L1C имеются катушки различных длин l, диаметров 2rи числа витков N(соответствующие значения для номера каждой катушки представлены в таблице 2), емкость считается известной и установлена в разъёмник. Расчетные формулы: 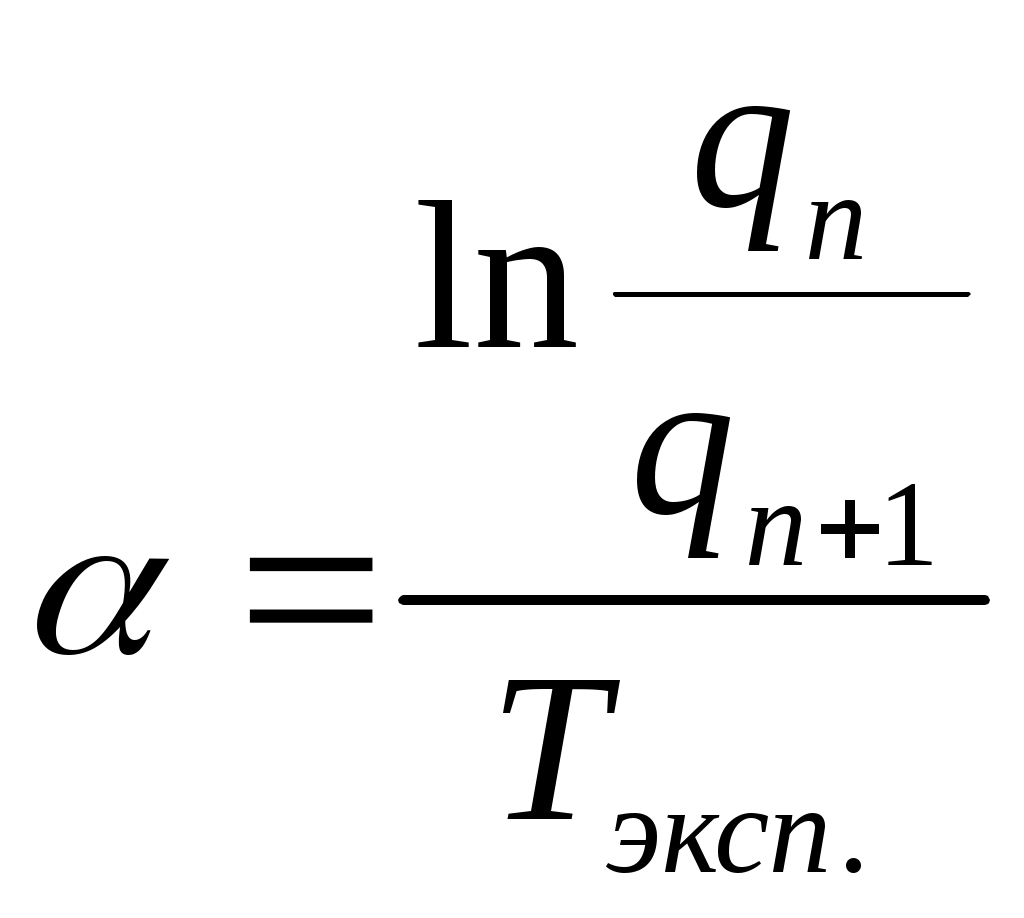 - коэффициент затухания; - коэффициент затухания;Таблица №1. Исследования основных параметров колебательного контура.
Таблица №2. Характеристики катушек
Примеры вычислений: Погрешности: При выполнении данной работы следует учитывать только погрешности приборов, которые составляют: Графики зависимости: График №1 для L1= f(N) для катушек №№ 3,6,7 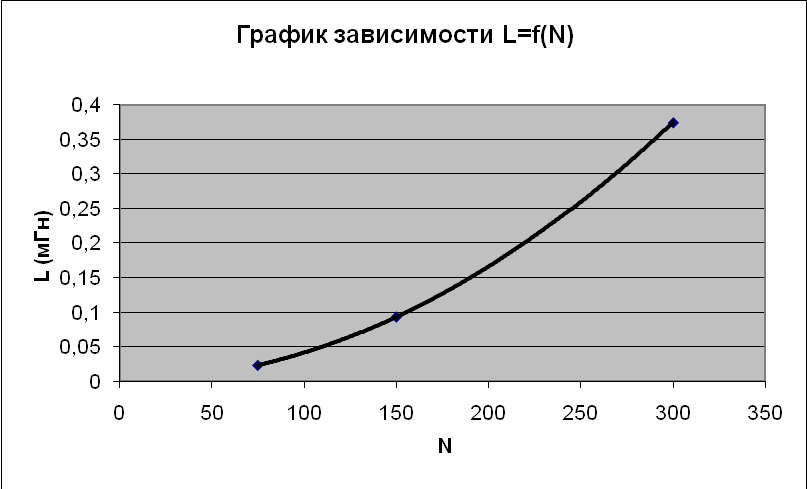 График №2 для L1= f(l) для катушек №№ 1,4,5 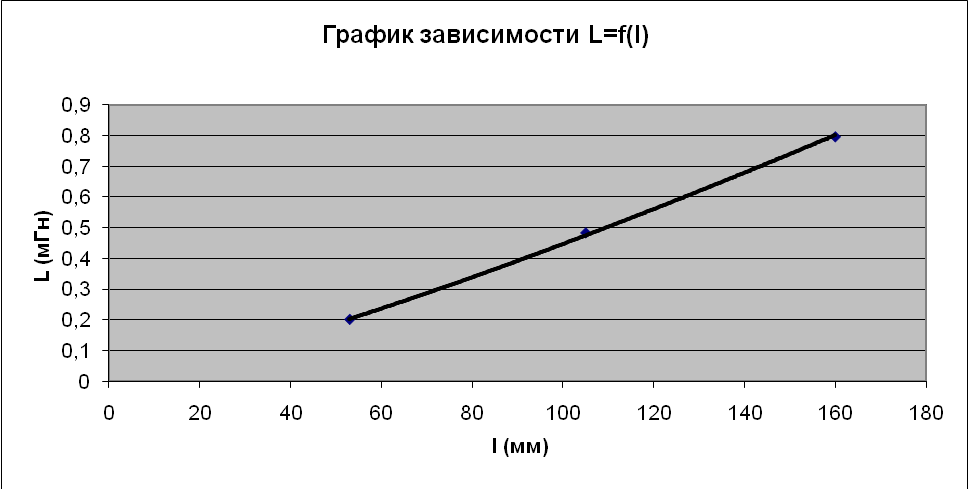 График №3 для L1= f(r) для катушек №№ 1,2,3 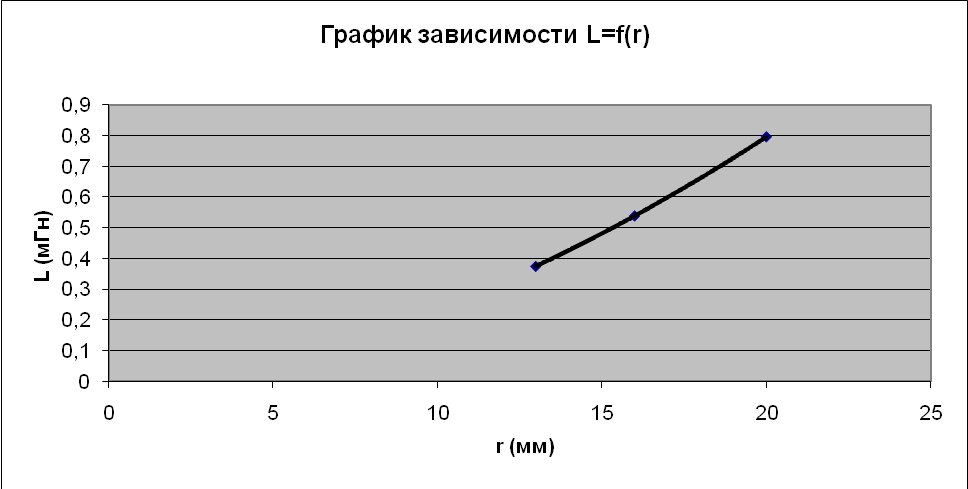 График №4 для Т = f(L1) для всех катушек. 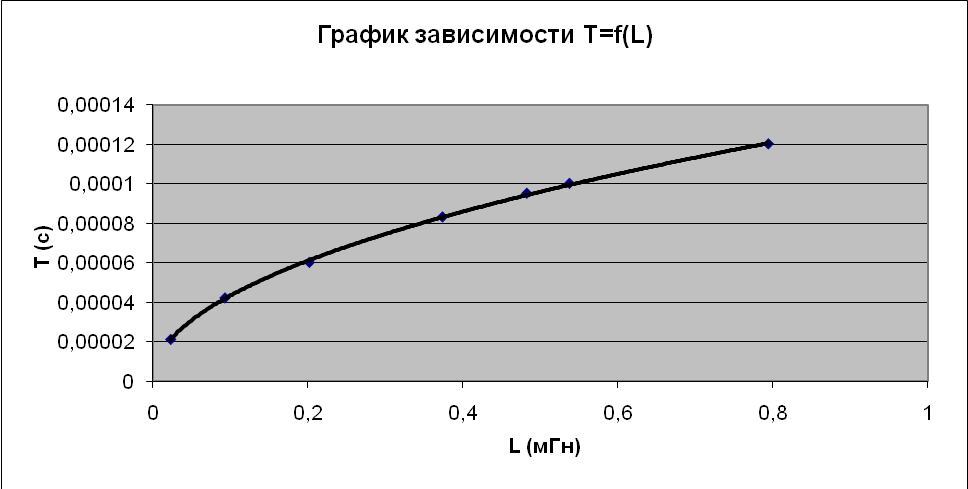 Вывод: в данной лабораторной работе мною были произведены измерения и вычисления для определения индуктивности и добротности электромагнитного контура. По результатам проделанной работы были получены зависимости L1= f(N), L1= f(l), L1 = f(r), Т = f(L1);которые не существенно откланяются, от теоретически ожидаемого результата. На графике зависимости L=f(N) видим параболическую зависимость, что соответствует подобной зависимости из формулы На графике зависимости L=f(l) видим прямую зависимость, что соответствует формуле На графике зависимости L=f(r) видим степенную зависимость и это соответствует подобной зависимости из формулы На графике зависимости T=f(L) видим корневую зависимость, что соответствует подобной зависимости из формулы |
