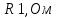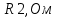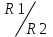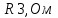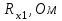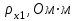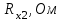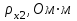ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ТОКОПРОВОДЯЩИХ МОДЕЛЕЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА. Измерение сопротивлений токопроводящих моделей при помощи моста уитстона
 Скачать 63.78 Kb. Скачать 63.78 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ТВ отчет По виртуальной лабораторной работе №8 по дисциплине «Физика» Тема: “ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ТОКОПРОВОДЯЩИХ МОДЕЛЕЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА”
Санкт-Петербург 2022 ЛАБОРАТОРНАЯ РАБОТА № 8 ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ТОКОПРОВОДЯЩИХ МОДЕЛЕЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА Цель работы: ознакомление с методом измерения сопротивлений при помощи моста постоянного тока; приобретение навыков расчета сопротивлений проводников переменного сечения; определение удельных сопротивлений материалов токопроводящих моделей. Приборы и принадлежности: стенд для сборки измерительной цепи; токопроводящие модели; магазины образцовых сопротивлений; нуль-индикатор (гальванометр); источник тока. Общие сведения Сопротивление проводников зависит от их формы и размеров, от рода вещества и его состояния. Для проводников в форме цилиндров постоянного поперечного сечения сопротивление равно: 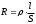 , (1) , (1) где l и S - длина и сечение проводника, соответственно; - удельное сопротивление материала проводника. Удельное сопротивление является одной из основных электрических характеристик вещества. Оно определяется тока в веществе при заданной величине напряженности электрического поля 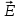 (закон Ома в дифференциальной форме): (закон Ома в дифференциальной форме):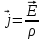 а также удельную тепловую мощность тока 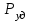 , т.е. количество тепла, выделяющегося в единицу времени в единицу объема (закон Джоуля - Ленца в дифференциальной форме): , т.е. количество тепла, выделяющегося в единицу времени в единицу объема (закон Джоуля - Ленца в дифференциальной форме): 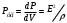 . .Зная значение 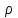 , можно рассчитать размеры проводника, требуемые для получения заданного его сопротивления, или наоборот – значение сопротивления при известных геометрических размерах проводника. , можно рассчитать размеры проводника, требуемые для получения заданного его сопротивления, или наоборот – значение сопротивления при известных геометрических размерах проводника.Выражение (1) имеет ограниченное применение: оно не пригодно для проводников переменного сечения, в которых плотность тока не одинакова в любом сечении, например, при расчете сопротивления утечки цилиндрического конденсатора, заполненного проводящей средой. Расчет таких сопротивлений производят, разбивая (руководствуясь соображениями симметрии) проводники (или проводящую среду) на множество элементов длиной 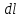 и поперечным сечением и поперечным сечением 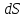 так, чтобы плотность тока в любой точке отдельного элемента была одинаковой. Сопротивление каждого отдельного элемента равно так, чтобы плотность тока в любой точке отдельного элемента была одинаковой. Сопротивление каждого отдельного элемента равно 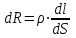 , а сопротивление проводника на участке от , а сопротивление проводника на участке от 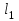 до до 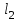 будет будет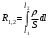 , ,где S - поперечное сечение проводника, представленное в виде некоторой функции от 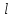 . . Если такое разбиение невозможно, или зависимость S от 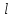 слишком сложна, используют подобие электрического поля в однородной проводящей среде с током электростатическому полю в диэлектрике при условии, что удельное сопротивление проводящей среды много больше удельного сопротивления материала электродов. Иначе говоря, распределение потенциала в проводящей среде с током окажется таким же, что и в диэлектрике (или вакууме), если, не меняя размеров и формы электродов, их взаимного расположения и разности потенциалов между ними, проводящую среду заменить диэлектрической. При этом выполняется соотношение слишком сложна, используют подобие электрического поля в однородной проводящей среде с током электростатическому полю в диэлектрике при условии, что удельное сопротивление проводящей среды много больше удельного сопротивления материала электродов. Иначе говоря, распределение потенциала в проводящей среде с током окажется таким же, что и в диэлектрике (или вакууме), если, не меняя размеров и формы электродов, их взаимного расположения и разности потенциалов между ними, проводящую среду заменить диэлектрической. При этом выполняется соотношение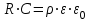 (2) (2)где R - сопротивление утечки между двумя электродами в проводящей среде с удельным сопротивлением ; C - емкость конденсатора, образованного этими же электродами в среде с относительной диэлектрической проницаемостью . Таким образом, расчет сопротивления утечки между электродами в проводящей среде можно свести к расчету емкости конденсатора, образованного этими же электродами, т.е., по существу, к задаче электростатики. Расчет емкости конденсатора производится по формуле , где Q - заряд на одном из электродов; - разность потенциалов между электродами. Выражение для получается из связи напряженности E и потенциала электрического поля (E = –grad): 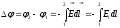 , (3) , (3) где El - проекция вектора Е на направление l, вдоль которого производится интегрирование. Выражение для El, подставляемое в формулу (3), находится по принципу суперпозиции напряженностей электрических полей E1 и E2 создаваемых зарядами электродов Q и -Q, либо по теореме Гаусса: 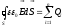 . .В результате расчета получается выражение для 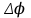 , представленное функцией заряда Q, геометрических размеров, формы и взаимного расположения электродов. В этом выражении коэффициент пропорциональности перед и - есть величина, обратная емкости конденсаторы, образованного электродами. Формула для расчета сопротивления утечки между электродами в проводящей среде получается из соотношения (2). , представленное функцией заряда Q, геометрических размеров, формы и взаимного расположения электродов. В этом выражении коэффициент пропорциональности перед и - есть величина, обратная емкости конденсаторы, образованного электродами. Формула для расчета сопротивления утечки между электродами в проводящей среде получается из соотношения (2).Следует также отметить, что из-за подобия распределения полей в проводящей среде и в диэлектрике проводящая среда с током может служить моделью для исследования электростатических полей. Например, вместо трудоемких расчетов или непосредственного измерения емкости какой-либо системы проводников сложной формы поместить модели этих проводников в проводящую среду, измерить сопротивление между ними, а затем найти емкость, используя соотношение (2). Во многих случаях такая методика оказывается предпочтительнее. Протокол наблюдений Для коаксиального кабеля 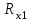
Внешний радиус Внутренний радиус Толщина проводящей поверхности Для двухпроводной линии 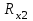
Радиус двухпроводной линии Длина двухпроводной линии Толщина Выполнил: Гоношилкин Даниил Юрьевич Факультет ФРТ Группа № 1105 “__” ___________ 2021 Преподаватель: Дедык А.И. Вопросы: Выведите условия баланса моста. Дайте определение мощности тока. Чем отличаются полная мощность, мощность. выделяющаяся во внешней и внутренних цепях. Мощность электрического тока — это физическая величина, определяемая как количество работы, которая совершается источником электрического напряжения для переноса электрического заряда (q) по проводнику за единицу времени t. Мощность, развиваемая источником тока во всей цепи, называется полной мощностью. 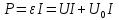 Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностью Pпол=UI. Величина UoI соответствует мощности, бесполезно расходуемой внутри источника, Ее называют мощностью потерь Po=UoI. Таким образом, полная мощность равна сумме полезной мощности и мощности потерь Pоб=Pпол+P0. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||