Изоморфизм Евклидовых векторных пространств. Изоморфизм Евклидвых векторных пространств. Изоморфизм евклидовых векторных пространств
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Изоморфизм евклидовых векторных пространств Определение 4.3. Два линейных пространства 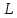 и и 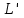 называют изоморфными, если существует линейное биективное отображение называют изоморфными, если существует линейное биективное отображение 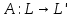 . При этом само отображение A называют изоморфизмом линейных пространств . При этом само отображение A называют изоморфизмом линейных пространств 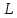 и и 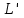 . .Как следует из данного определения, изоморфизм представляет собой линейный оператор нулевого дефекта и максимального ранга. Примером изоморфизма линейного пространства в себя является тождественный оператор. Теорема об изоморфизме евклидовых пространств Теорема 4.2. Два конечномерных линейных пространства изоморфны тогда и только тогда, когда они имеют одинаковую размерность. Пусть линейные пространства 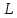 и и 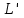 имеют одинаковую размерность n. Мы докажем изоморфность этих линейных пространств, построив отображение имеют одинаковую размерность n. Мы докажем изоморфность этих линейных пространств, построив отображение 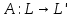 , являющееся изоморфизмом. Для этого выберем произвольные базисы , являющееся изоморфизмом. Для этого выберем произвольные базисы 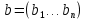 в линейном пространстве в линейном пространстве 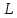 и и 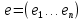 в линейном пространстве в линейном пространстве 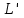 . Любой вектор . Любой вектор 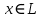 может быть разложен в базисе b, т.е. представлен в виде может быть разложен в базисе b, т.е. представлен в виде 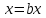 , где x — столбец координат этого вектора в базисе b. Вектору , где x — столбец координат этого вектора в базисе b. Вектору 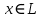 поставим в соответствие вектор поставим в соответствие вектор 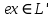 , который в базисе eлинейного пространства , который в базисе eлинейного пространства 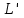 имеет те же координаты, что и вектор x в базисе b. Заданное таким образом отображение имеет те же координаты, что и вектор x в базисе b. Заданное таким образом отображение 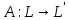 является линейным оператором. Действительно, если взять произвольные векторы является линейным оператором. Действительно, если взять произвольные векторы 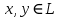 со столбцами координат со столбцами координат 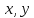 то то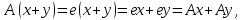 так как при сложении векторов их координаты складываются. Точно так же при умножении вектора x со столбцом координат x на произвольное число 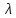 получаем получаем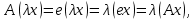 где опять-таки использованы правила умножения вектора на где опять-таки использованы правила умножения вектора на число в координатах. Линейный оператор А является инъективным, так как равенство 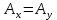 означает, что означает, что 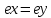 или или 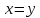 в силу единственности разложения вектора по базису. Поэтому в силу единственности разложения вектора по базису. Поэтому 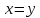 . .Линейный оператор А является сюрьективным, так как любой вектор 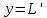 с координатами y в базисе e является образом вектора с координатами y в базисе e является образом вектора 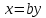 с теми же координатами y, что и y, но относительно „своего“ базиса b. Линейное, инъективное и сюрьективное отображение, по определению 4.3, и есть изоморфизм. Следовательно, линейные пространства с теми же координатами y, что и y, но относительно „своего“ базиса b. Линейное, инъективное и сюрьективное отображение, по определению 4.3, и есть изоморфизм. Следовательно, линейные пространства 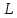 и и 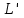 изоморфны, при этом изоморфизмом является построенный нами линейный оператор А. изоморфны, при этом изоморфизмом является построенный нами линейный оператор А.Предположим теперь, что линейные пространства 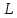 и и 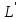 изоморфны и пусть отображение изоморфны и пусть отображение 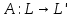 является соответствующим изоморфизмом. В n-мерном линейном пространстве является соответствующим изоморфизмом. В n-мерном линейном пространстве 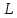 выберем некоторый базис выберем некоторый базис 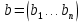 и докажем, что система векторов и докажем, что система векторов 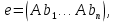 состоящая из образов базисных векторов, является базисом в состоящая из образов базисных векторов, является базисом в 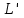 . .Во-первых, система векторов е линейно независима. Возьмем произвольную линейную комбинацию этой системы векторов с некоторыми коэффициентами 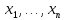 и приравняем нулевому вектору 0' в и приравняем нулевому вектору 0' в 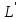 : :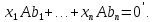 Левая часть равенства является образом некоторого вектора x: 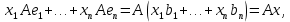 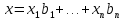 , координатами которого в выбранном базисе b являются коэффициенты линейной комбинации. Так как отображение A инъективно, а нулевой вектор из , координатами которого в выбранном базисе b являются коэффициенты линейной комбинации. Так как отображение A инъективно, а нулевой вектор из 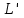 является образом нулевого вектора из является образом нулевого вектора из 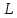 , заключаем, что , заключаем, что 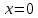 , поскольку , поскольку 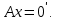 Итак, Итак,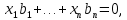 а это возможно, лишь если все коэффициенты линейной комбинации равны нулю. Во-вторых, любой вектор 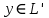 можно представить в виде линейной комбинации системы векторов e. В самом деле, так как отображение А сюрьективно, вектор у является образом некоторого вектора x, имеющего в базисе b столбец координат x. Тогда можно представить в виде линейной комбинации системы векторов e. В самом деле, так как отображение А сюрьективно, вектор у является образом некоторого вектора x, имеющего в базисе b столбец координат x. Тогда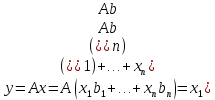 , ,и мы получаем разложение у по системе векторов е, коэффициентами в котором являются координаты вектора x в базисе b. Система векторов е линейно независима, и в ней можно разложить любой вектор линейного пространства 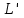 . Значит, эта система является базисом в . Значит, эта система является базисом в 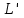 . При этом количество векторов в eсовпадает с количеством векторов в базисе b линейного пространства . При этом количество векторов в eсовпадает с количеством векторов в базисе b линейного пространства 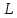 , следовательно, размерности пространств , следовательно, размерности пространств 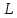 и и 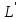 совпадают. совпадают. Следствие 4.1. Все n-мерные линейные пространства изоморфны линейному арифметическому пространству 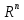 . .Построенный в доказательстве теоремы 4.2 изоморфизм связан с выбором базисов в линейных пространствах 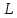 и и 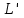 . Если в той или иной ситуации мы можем считать, что базис в линейном пространстве фиксирован, то вместо абстрактного n-мерного линейного пространства можно использовать „стандартное“ линейное арифметическое пространство . Если в той или иной ситуации мы можем считать, что базис в линейном пространстве фиксирован, то вместо абстрактного n-мерного линейного пространства можно использовать „стандартное“ линейное арифметическое пространство 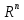 . Все рассуждения и выкладки в линейном арифметическом пространстве носят более конкретный и интуитивно понятный характер. . Все рассуждения и выкладки в линейном арифметическом пространстве носят более конкретный и интуитивно понятный характер.Но считать базис в линейном пространстве фиксированным не всегда приемлемо, поэтому нельзя считать идентичными произвольные n-мерные линейные пространства. Обычно отождествляют линейные пространства, между которыми существует „естественный“ изоморфизм, не связанный с выбором того или иного базиса. Например, как линейные пространства тождественны линейное пространство матриц типа 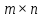 и линейное арифметическое пространство и линейное арифметическое пространство 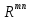 , так как между ними возникает изоморфизм, если установить соответствие между элементами матрицы типа , так как между ними возникает изоморфизм, если установить соответствие между элементами матрицы типа 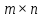 и компонентами mn-мерного арифметического вектора. Точно так же можно не различать линейное пространство строк длины n и линейное пространство столбцов высоты n. и компонентами mn-мерного арифметического вектора. Точно так же можно не различать линейное пространство строк длины n и линейное пространство столбцов высоты n.Указанное отождествление линейных пространств позволяет записывать векторы линейного арифметического пространства в зависимости от ситуации и как матрицы-строки, и как матрицы-столбцы. Напомним, что элементами n-мерного линейного арифметического пространства являются упорядоченные совокупности из n чисел. Порядок чисел в каждой такой совокупности можно задавать различными способами, и запись ее в строку или столбец — лишь две возможности из бесчисленного множества способов. Пример 4.6. В линейном пространстве 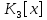 многочленов переменного x степени не выше трех элементы многочленов переменного x степени не выше трех элементы 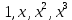 образуют базис. Этому базису соответствует изоморфизм между образуют базис. Этому базису соответствует изоморфизм между 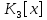 и и 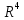 , при котором многочлену , при котором многочлену 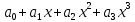 сопоставляется арифметический вектор ( сопоставляется арифметический вектор (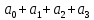 ). ).Ортогональное дополнение к подпространству Как следует из теоремы 2.7, в произвольном линейном пространстве 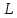 любое линейное подпространство любое линейное подпространство 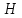 имеет прямое дополнение, т.е. такое линейное подпространство имеет прямое дополнение, т.е. такое линейное подпространство 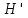 , что , что 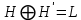 . Такое линейное подпространство . Такое линейное подпространство 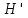 не является единственным. Однако в случае евклидова пространства среди всех возможных прямых дополнений к данному линейному подпространству одно выделяется. не является единственным. Однако в случае евклидова пространства среди всех возможных прямых дополнений к данному линейному подпространству одно выделяется.Определение 3.8. Ортогональным дополнением линейного подпространства 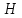 в евклидовом пространстве в евклидовом пространстве 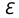 называют множество называют множество  всех векторов всех векторов 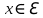 , ортогональных каждому вектору линейного подпространства , ортогональных каждому вектору линейного подпространства 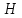 . .Пример 3.15. В евклидовом пространстве 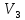 свободных векторов рассмотрим линейное подпространство векторов, параллельных данной плоскости (см. пример 2.1). Тогда ортогональным дополнением свободных векторов рассмотрим линейное подпространство векторов, параллельных данной плоскости (см. пример 2.1). Тогда ортогональным дополнением  будет множество векторов, перпендикулярных к этой плоскости (рис. 3.6, а), в то время как в качестве прямого дополнения будет множество векторов, перпендикулярных к этой плоскости (рис. 3.6, а), в то время как в качестве прямого дополнения 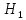 можно взять подпространство векторов, коллинеарных произвольной прямой, пересекающей плоскость в единственной точке, т.е. не параллельной плоскости и не лежащей в этой плоскости (рис. 3.6, б). Отметим, что в данном случае можно взять подпространство векторов, коллинеарных произвольной прямой, пересекающей плоскость в единственной точке, т.е. не параллельной плоскости и не лежащей в этой плоскости (рис. 3.6, б). Отметим, что в данном случае  является линейным подпространством в является линейным подпространством в 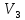 . . Теорема 3.6. Ортогональное дополнение  линейного подпространства линейного подпространства 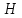 в евклидовом подпространстве в евклидовом подпространстве 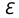 является линейным подпространством в является линейным подпространством в 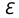 , причем , причем 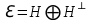 и и 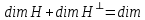 Чтобы доказать, что  является линейным подпространством в является линейным подпространством в 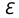 , нужно проверить условия 1) и 2) определения 2.1. Взяв два произвольных вектора x и y, принадлежащих , нужно проверить условия 1) и 2) определения 2.1. Взяв два произвольных вектора x и y, принадлежащих  , умножим скалярно их сумму на произвольный вектор , умножим скалярно их сумму на произвольный вектор 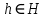 . .Получим: 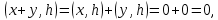 т.е. для любых векторов 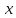 и и 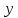 из множества из множества  их сумма их сумма 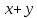 принадлежит тому же множеству. принадлежит тому же множеству.Теперь рассмотрим произведение вектора 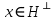 на произвольное действительное число на произвольное действительное число 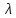 . Для произвольного вектора . Для произвольного вектора 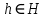 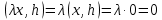 , ,и поэтому 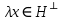 , если , если 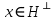 . Следовательно, . Следовательно,  является линейным подпространством в является линейным подпространством в 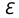 . .Отметим, что любой вектор 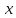 , принадлежащий пересечению , принадлежащий пересечению 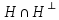 , ортогонален самому себе: , ортогонален самому себе: 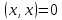 , так как любой вектор , так как любой вектор  из ортогонален любому вектору подпространства из ортогонален любому вектору подпространства 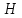 . Но вектор ортогонален самому себе лишь в том случае, когда он нулевой (аксиома г) скалярного умножения). Поэтому . Но вектор ортогонален самому себе лишь в том случае, когда он нулевой (аксиома г) скалярного умножения). Поэтому 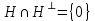 , а сумма , а сумма 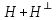 рассматриваемых линейныx подпространств является прямой (см. теорему 2.3). Докажем, что эта прямая сумма совпадает со всем евклидовым пространством рассматриваемых линейныx подпространств является прямой (см. теорему 2.3). Докажем, что эта прямая сумма совпадает со всем евклидовым пространством 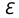 . .Выберем некоторый ортонормированный базис 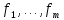 в линейном подпространстве в линейном подпространстве 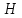 и дополним его до базиса и дополним его до базиса 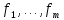 во всем евклидовом пространстве во всем евклидовом пространстве 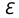 , , 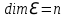 . Исходя из этого базиса построим при помощи процесса Грама — Шмидта ортонормированный базис . Исходя из этого базиса построим при помощи процесса Грама — Шмидта ортонормированный базис 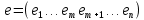 . Так как первые . Так как первые 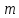 векторов векторов 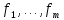 исходного базиса попарно ортогональны и имеют единичную длину, процесс ортогонализации оставит их без изменения, т.е. исходного базиса попарно ортогональны и имеют единичную длину, процесс ортогонализации оставит их без изменения, т.е. 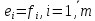 . Векторы . Векторы 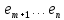 ортогональны каждому из векторов ортогональны каждому из векторов 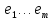 базиса линейного подпространства базиса линейного подпространства 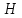 и, следовательно, ортогональны и, следовательно, ортогональны 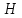 , так как , так как 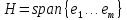 . Поэтому все они попадают в ортогональное дополнение . Поэтому все они попадают в ортогональное дополнение  . .Рассмотрим произвольный вектор 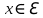 и запишем его разложение по базису и запишем его разложение по базису 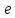 : :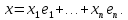 Легко увидеть, что 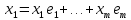 есть вектор из есть вектор из 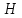 , а , а 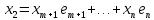 есть вектор из есть вектор из  , при этом , при этом 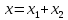 . Следовательно, . Следовательно, 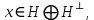 и так как вектор и так как вектор 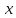 выбирался произвольно, то выбирался произвольно, то 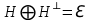 . .Согласно следствию из теоремы 2.5, из соотношения 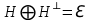 вытекает следующее равенство для размерностей: вытекает следующее равенство для размерностей: 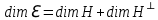 . .Следствие 3.1. Каково бы ни было линейное подпространство 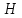 в евклидовом пространстве в евклидовом пространстве 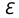 , любой вектор , любой вектор 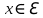 можно однозначно представить в виде можно однозначно представить в виде 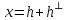 , (3.11) , (3.11)где 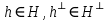 . .Действительно, это утверждение означает, что 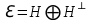 . .Вектор 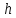 в разложении (3.11) называют ортогональной проекцией вектора в разложении (3.11) называют ортогональной проекцией вектора 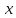 на линейное подпространство на линейное подпространство 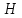 , а вектор , а вектор 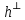 — ортогональной составляющей вектора — ортогональной составляющей вектора 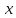 относительно линейного подпространства относительно линейного подпространства 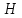 . .Как построить ортогональное дополнение к данному линейному подпространству? Пусть линейное подпространство 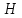 определено наиболее распространенным способом — как линейная оболочка некоторой системы векторов определено наиболее распространенным способом — как линейная оболочка некоторой системы векторов 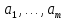 . .Согласно определению 3.8 ортогонального дополнения, любой вектор 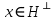 должен быть ортогонален каждому из векторов должен быть ортогонален каждому из векторов 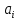 : :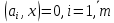 (3.12) (3.12)Наоборот, если вектор 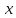 удовлетворяет системе равенств (3.12), т.е. он ортогонален каждому из векторов удовлетворяет системе равенств (3.12), т.е. он ортогонален каждому из векторов 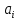 , то этот вектор ортогонален и любой линейной комбинации системы векторов , то этот вектор ортогонален и любой линейной комбинации системы векторов 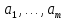 (см. 3.5). Значит, (см. 3.5). Значит, 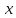 ортогонален каждому вектору линейного подпространства ортогонален каждому вектору линейного подпространства 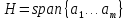 и принадлежит линейному подпространству и принадлежит линейному подпространству  . .Итак, система уравнений (3.12) описывает ортогональное дополнение линейного подпространства 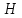 . Запишем эту систему в координатах в некотором ортонормированном базисе . Запишем эту систему в координатах в некотором ортонормированном базисе 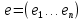 . Пусть векторы . Пусть векторы 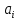 в этом базисе имеют разложения в этом базисе имеют разложения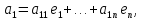 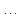 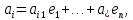 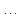 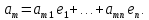 Координаты произвольного вектора 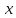 в том же базисе обозначим в том же базисе обозначим 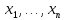 . Т.е. полагаем, что . Т.е. полагаем, что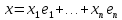 . .Тогда в ортонормированном базисе 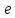 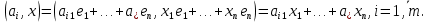 Таким образом, система (3.12), записанная в координатах относительно ортонормированного базиса 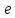 , имеет вид , имеет вид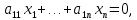 …… (3.13) …… (3.13) 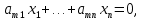 т.е. представляет собой однородную систему из т.е. представляет собой однородную систему из 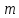 линейных алгебраических уравнений с линейных алгебраических уравнений с 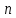 неизвестными. Строки матрицы А этой системы совпадают с наборами координат векторов неизвестными. Строки матрицы А этой системы совпадают с наборами координат векторов 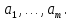 Поэтому матрица А имеет ранг, равный рангу системы векторов Поэтому матрица А имеет ранг, равный рангу системы векторов 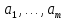 , т.е. этот ранг совпадает с размерностью линейного подпространства , т.е. этот ранг совпадает с размерностью линейного подпространства  . .Каждое решение системы (3.13) представляет собой набор координат некоторого вектора из  и наоборот, любой вектор из и наоборот, любой вектор из  описывает решение системы (3.13). Поэтому можно сказать, что множество всех решений этой системы есть линейное подпространство описывает решение системы (3.13). Поэтому можно сказать, что множество всех решений этой системы есть линейное подпространство  . Согласно теореме 3.6, это подпространство имеет размерность . Согласно теореме 3.6, это подпространство имеет размерность 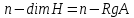 . Множество решений однородной системы линейных алгебраических уравнений (СЛАУ) описывается при помощи фундаментальной системы решений. Напомним, что столбцы фундаментальной системы решений линейно независимы, а любое решение однородной СЛАУ представляется в виде линейной комбинации столбцов фундаментальной системы решений. Другими словами, фундаментальная система решений — это базис в подпространстве всех решений данной однородной СЛАУ. Каждый столбец фундаментальной системы решений представляет собой координатную запись вектора линейного подпространства . Множество решений однородной системы линейных алгебраических уравнений (СЛАУ) описывается при помощи фундаментальной системы решений. Напомним, что столбцы фундаментальной системы решений линейно независимы, а любое решение однородной СЛАУ представляется в виде линейной комбинации столбцов фундаментальной системы решений. Другими словами, фундаментальная система решений — это базис в подпространстве всех решений данной однородной СЛАУ. Каждый столбец фундаментальной системы решений представляет собой координатную запись вектора линейного подпространства  в выбранном базисе в выбранном базисе 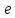 евклидова пространства евклидова пространства 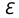 , при этом такие векторы в совокупности образуют базис подпространства , при этом такие векторы в совокупности образуют базис подпространства  . Мы здесь можем не различать фундаментальную систему решений системы (3.13) и соответствующий ей базис ортогонального дополнения . Мы здесь можем не различать фундаментальную систему решений системы (3.13) и соответствующий ей базис ортогонального дополнения  . .Пример 3.16. Пусть линейное подпространство 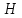 представляет собой линейную оболочку системы векторов, заданных координатами в некотором фиксированном ортонормированном базисе представляет собой линейную оболочку системы векторов, заданных координатами в некотором фиксированном ортонормированном базисе 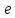 четырехмерного евклидова пространства четырехмерного евклидова пространства 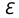 : :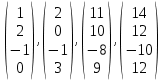 Найдем какой-либо базис ортогонального дополнения  . .Записываем систему вида (3.13), используя координаты векторов 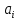 : :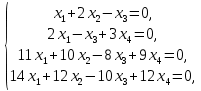 и находим ее фундаментальную систему решений. Это можно сделать, например, с помощью приведения матрицы системы к ступенчатому виду методом элементарных преобразований [III]. В качестве базисных переменных выберем 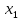 и и 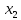 . Тогда фундаментальная система решений будет содержать два решения, например: . Тогда фундаментальная система решений будет содержать два решения, например: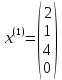 , , 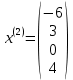 . .Столбцы найденной фундаментальной системы решений представляют собой координаты двух векторов 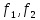 из из 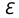 , образующих базис линейного подпространства , образующих базис линейного подпространства  , но этот базис не является ортонормированным. Чтобы получить ортонормированный базис , но этот базис не является ортонормированным. Чтобы получить ортонормированный базис  , достаточно применить процесс ортогонализации Грама — Шмидта. Сделав это, находим векторы , достаточно применить процесс ортогонализации Грама — Шмидта. Сделав это, находим векторы 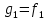 , ,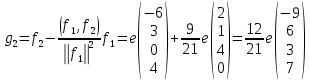 и ортонормированный базис в линейном пространстве  : :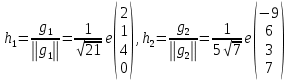 |
