Изучение электростатического поля методом моделирования
 Скачать 472.5 Kb. Скачать 472.5 Kb.
|
|
Лабораторная работа Э-1 ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ МЕТОДОМ МОДЕЛИРОВАНИЯ Цель работы: ознакомление с одним из методов моделирования электростатических полей, построение эквипотенциальных и силовых линий поля, расчёт его напряженности и оценка погрешности расчёта. Электростатическое поле представляет собой особый вид материи: оно возникает в пространстве, окружающем неподвижные электрические заряды и осуществляет взаимодействие между наэлектризованными телами.Электростатическое поле в каждой своей точке характеризуется силовой (напряжённость) и энергетической (потенциал) величинами. Напряжённость электростатического поля векторная величина, численно равная силе, с которой поле действует на положительный единичный пробный заряд, помещённый в данную точку поля 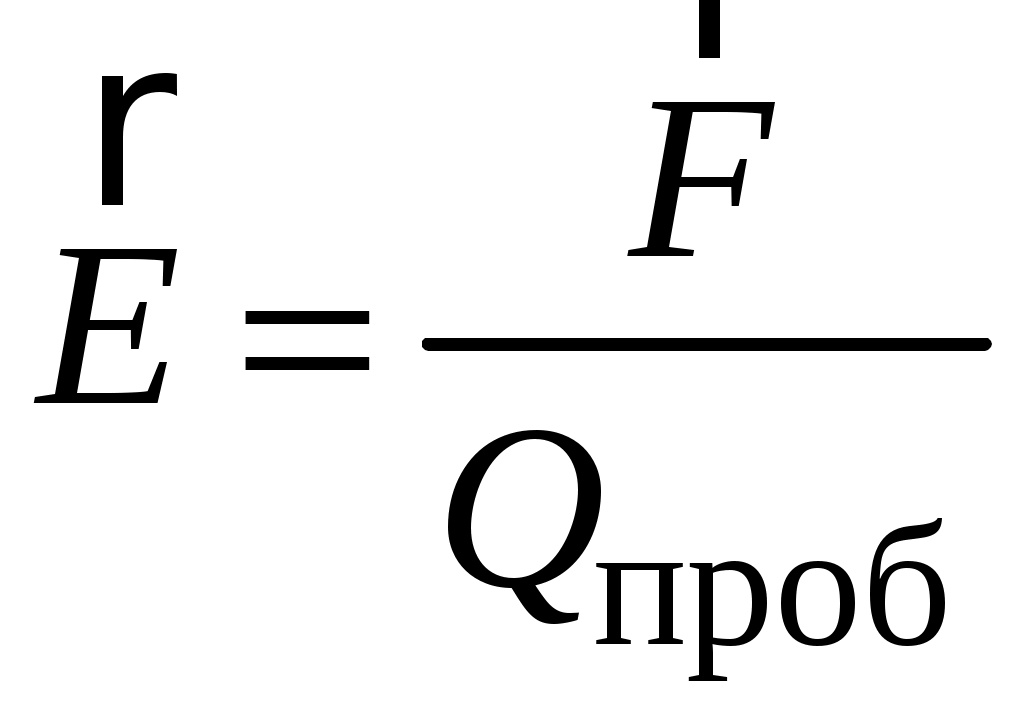 . (1.1) . (1.1)Направление вектора напряжённости совпадает с вектором силы, действующей на положительный заряд. Потенциал электростатического поля скалярная величина, численно равная потенциальной энергии единичного положительного пробного заряда, помещённого в данную точку поля 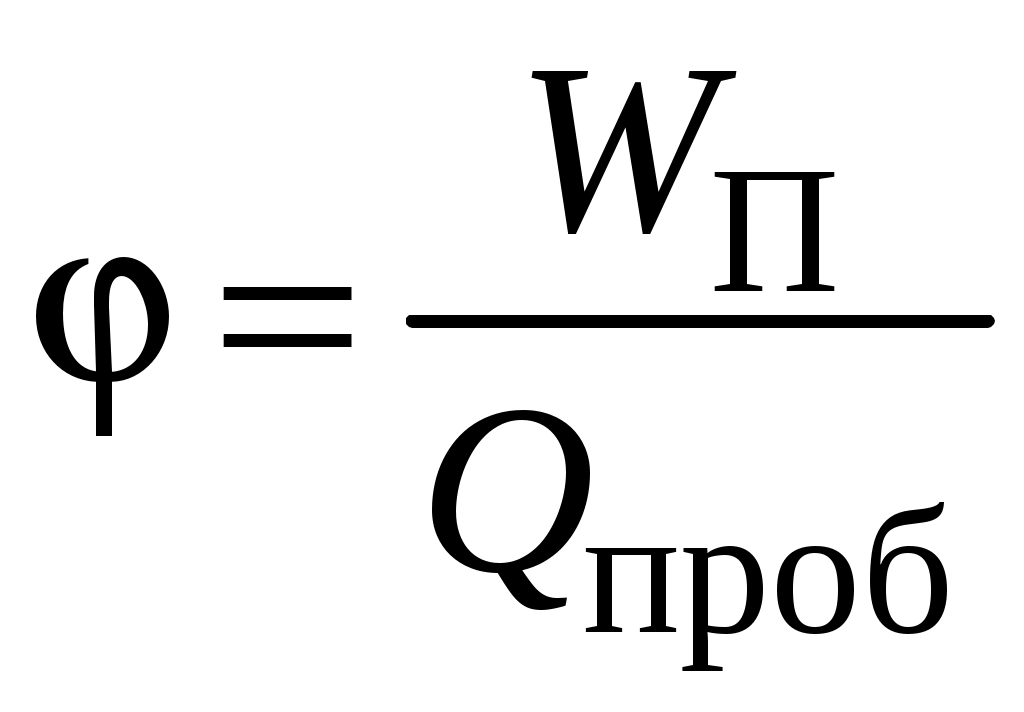 . (1.2) . (1.2) Следует заметить, что практический смысл имеет не сам потенциал, а разность потенциалов Для наглядного представления электростатических полей их принято изображать графически с помощью линий вектора напряжённости(силовых линий)и эквипотенциальных линий или поверхностей.Каждая линии вектора напряжённости проводится так, чтобы касательная к ней в каждой точке совпадала с направлением вектора напряжённости в этой точке. Тот факт, что касательная, как и любая прямая, имеет два взаимно противоположных направления, не вносит двузначности, поскольку силовой линии назначается вполне определённое направление (от положительного заряда к отрицательному), отмечаемое на чертеже стрелкой. Таким образом, каждой точке электрического поля соответствует свой вектор напряжённости. Поэтому силовые линии нигде не пересекаются между собой. (Если бы они пересеклись, то в точке пересечения имелось бы два разнонаправленных вектора Объединяя в электростатическом поле точки с одинаковым потенциалом, получают поверхности равного потенциала, или эквипотенциальные поверхности. Пересекаясь с плоскостью чертежа, эквипотенциальные поверхности образуют эквипотенциальные линии. Прочерчивая такие линии для разных значений потенциала, получают наглядное представление о том, как изменяется потенциал в данном поле. Перемещение пробного заряда по эквипотенциальной поверхности не требует совершения работы, так как потенциал остается величиной постоянной, то есть С другой стороны, эту работу можно найти по формуле 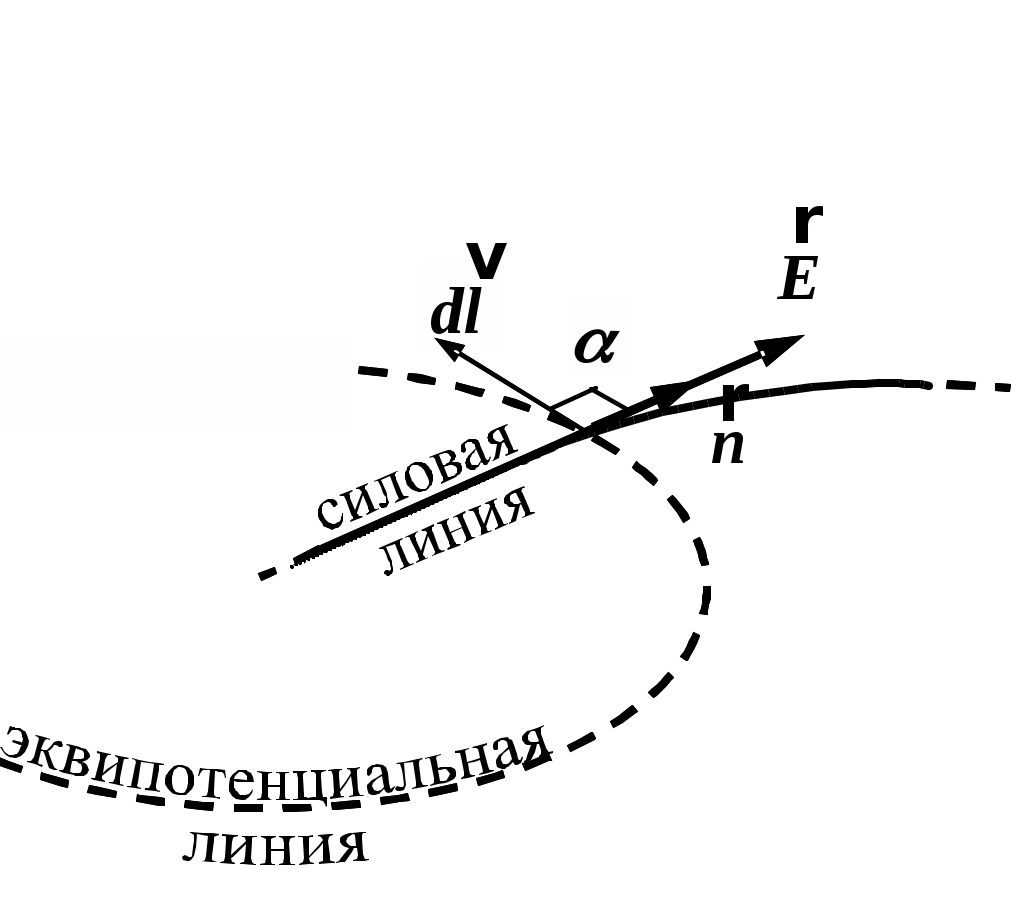 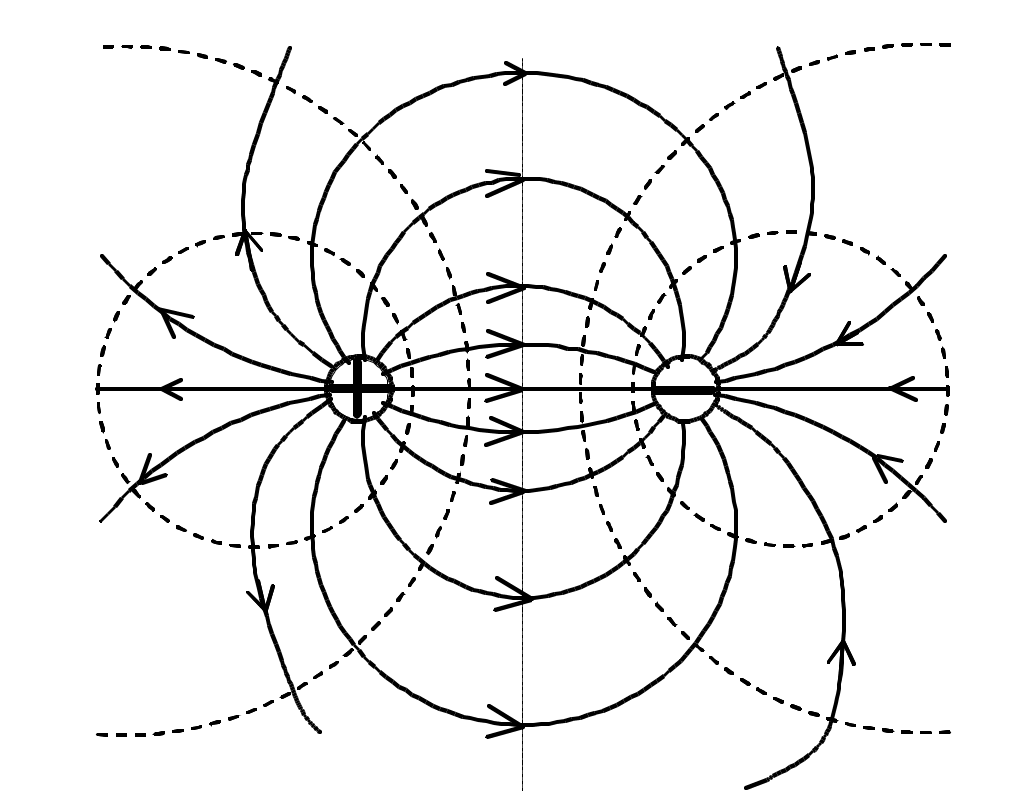 где – угол между векторами где – угол между векторами Рис. 1.1. Эквипотенциальные и силовые линии электрического поля Рис. 1.2. Пример построения силовых линий Значит, угол =90°. Таким образом, силовые линии всегда перпендикулярны к эквипотенциальнымповерхностям в точках их пересечения. На рис. 1.2 изображено плоское сечение электростатического поля двух разноимённо заряженных шаров. Силовые линии проведены здесь сплошными линиями, а эквипотенциальные линии – пунктирными. Однородным называется поле, вектор Потенциал наиболее быстро возрастает в направлении нормали где grad векторная величина, направление которой совпадает с направлением быстрейшего увеличения потенциала. Эта величина называется градиентом потенциала. Между напряжённостью и разностью потенциалов в каждой точке поля существует связь Если по формуле можно найти модуль вектора напряжённости на участке поля n. Описание метода исследования При исследовании сложных физических процессов широкое применение нашли модельные эксперименты. Различают физическое и математическоемоделирование. В первом случае модель и натура имеют одинаковую физическую природу, характер самого явления сохраняется, но геометрические размеры модели отличаются от натуры. Во втором случае физические явления разные, но их закономерности описываются одинаковыми дифференциальными уравнениями и граничными условиями. Такая тождественность математического описания позволяет заменить сложное исследование одного явления более простым исследованием другого [1]. Известно, что электрическое поле стационарного тока в слабопроводящей среде является потенциальным. Поэтому его можно использовать для моделирования электростатического поля заряженных тел в вакууме. При таком моделировании силовым линиям электростатического поля будут соответствовать линии тока, а поверхностям равного потенциала поверхности равных напряжений. Потенциалы различных точек модели могут быть измерены непосредственно вольтметром. Для исследования потенциала в электрических полях стационарного тока используются зонды, вводимые внутрь поля. Зондом является тонкий металлический стержень, хорошо изолированный по всей длине, кроме конца. Эксперимент значительно упростится, если проводить исследование плоского стационарного поля тока. В этом случае потенциалы измеряются при помощи зонда на поверхности слабопроводящей среды. Стационарное электрическое поле связано с наличием электрического тока, а это упрощает измерение разности потенциалов между любыми двумя точками поля. Для этого достаточно прикоснуться к этим точкам зондом, который подключен к вольтметру. Таким образом, на поверхности слабопроводящей среды могут быть получены линии равного потенциала. Силовые линии моделируемого поля строят так, чтобы касательные к ним были ортогональны к экспериментально полученным линиям равного потенциала (рис. 1.2). Описание установки Оборудование: регулируемый источник постоянного напряжения, слабопроводящая пластина с электродами, зонд, вольтметр. В настоящей работе в качестве слабопроводящей среды используется тонкий графитовый слой, нанесённый на стеклотекстолитовую пластину (рис. 1.3). Р 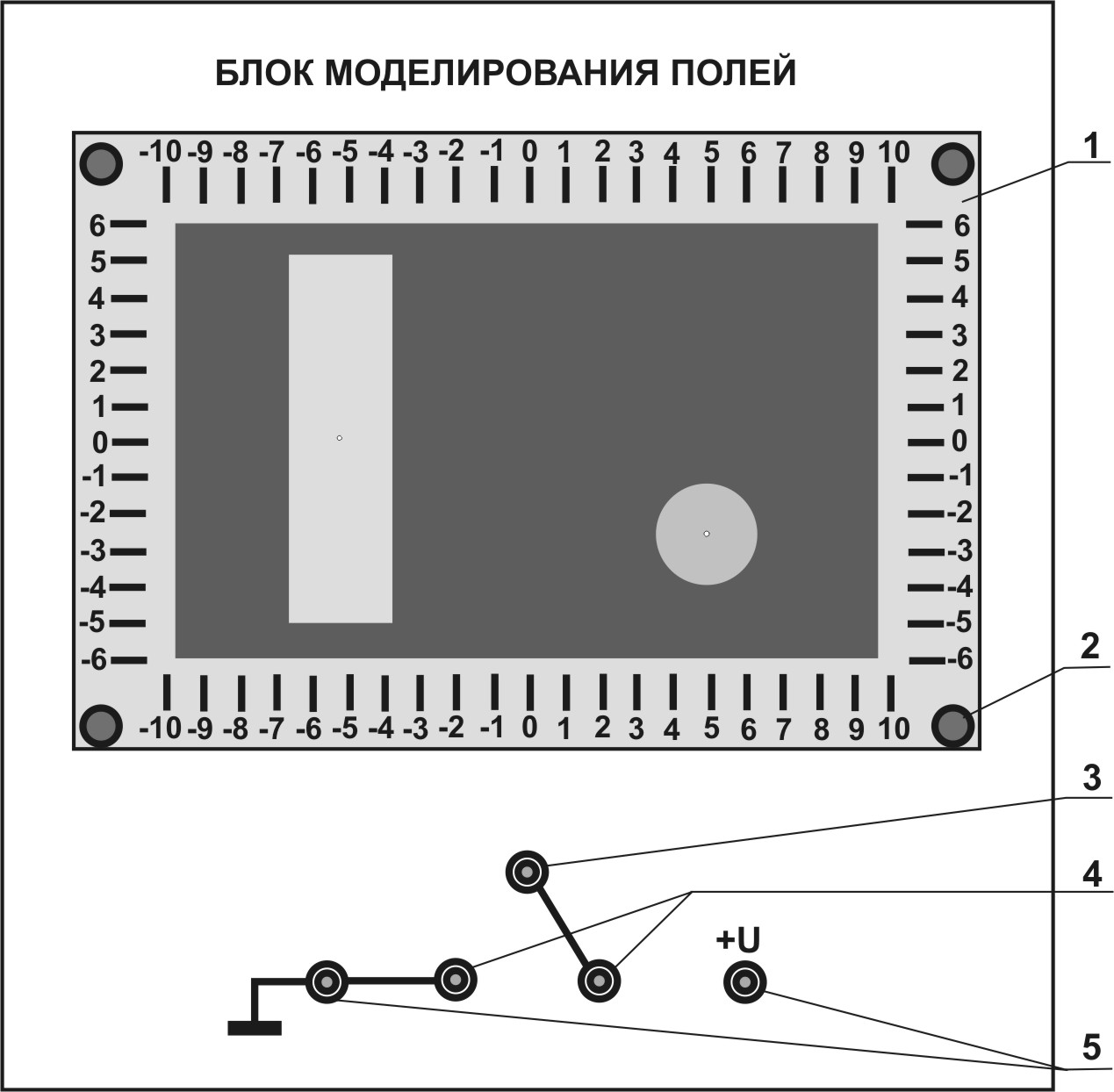 ис. 1.3. Блок моделирования полей: ис. 1.3. Блок моделирования полей:1 – слабопроводящая пластина для имитации электростатического поля с электродами и координатной сеткой; 2 – крепление пластины; 3 – вход для подключения зонда (щупа); 4 – входы для подключения вольтметра; 5 – входы для подключения регулируемого источника постоянного напряжения Для исследования электростатического поля собирают электрическую цепь по схеме, представленной на рис. 1.4. 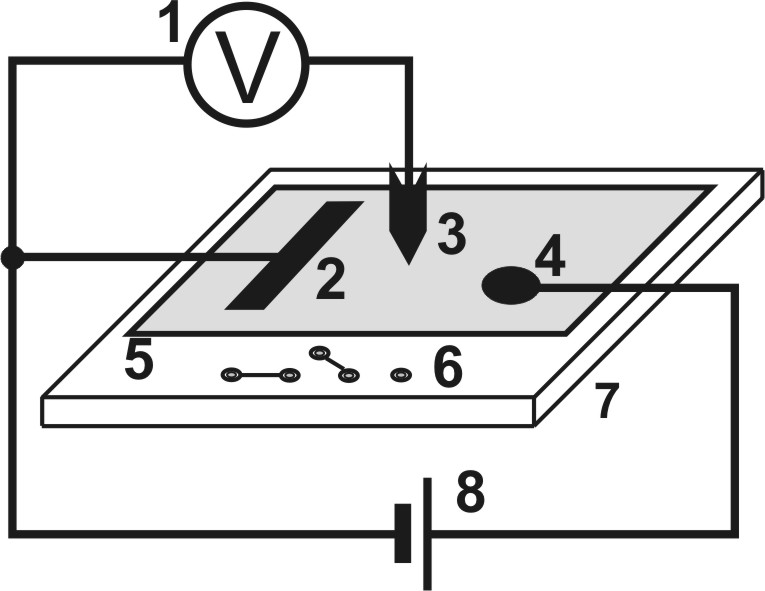 Рис. 1.4. Электрическая схема: 1 – вольтметр или мультиметр (режим V – вольтметр или мультиметр (режим V 2, 4 – электроды; 3 – зонд; 5 – слабо- Если зонд 3 поместить в произвольную точку пластины 5, то вольтметр 1 покажет значение потенциала поля в этой точке, измеренное относительно электрода 2, потенциал которого принимается равным нулю. Совокупность точек исследуемого поля с таким же значением потенциала образует эквипотенциальную поверхность. Выполнение работы 1. На лист миллиметровой бумаги формата А4 (210 2. Выбрать в качестве вольтметра для измерения постоянного напряжения один из мультиметров. Для этого переключатель рода работ мультиметра перевести в положение «V 3. Собрать электрическую цепь по схеме, приведенной на рис. 1.4. Внимание! На общий вход COM мультиметра подается отрицательное напряжение (провод «–» или «»), на вход V – положительное напряжение (провод «+»). 4. Кнопками «СЕТЬ» включить блок генераторов напряжения и блок мультиметров. Нажать кнопку «Исходная установка». 5. Кнопкой 6. Касаясь зондом электрода Э2, кнопками «Установка напряжения 0 … +15 В» установить по вольтметру заданную преподавателем разность потенциалов U между электродами. 7. Выбрать такой шаг изменения потенциала зонда 8. Около электрода с нулевым потенциалом найти точку поля с потенциалом 9. Повторить пп. 7, 8 для потенциалов: 10. Используя свойство ортогональности касательных к эквипотенциальным и силовым линиям электростатического поля, провести не менее пяти силовых линий. Их нужно проводить плавными кривыми без резких перегибов и обязательно указать их направление. Учтите, что с поверхностью электродов силовые линии должны пересекаться под прямым углом. 11. Выключить из сети блоки питания генераторов напряжений и мультиметров. Обработка результатов измерений 1. На наиболее однородной области моделируемого поля выбрать две соседние эквипотенциальные линии. На участке поля между ними рассчитать по формуле (1.8) модуль вектора напряжённости и указать его направление. Для однородного электростатического поля линии напряжённости параллельны вектору напряжённости. Оценка погрешности результатов измерений (см. приложение) 1. Систематическая относительная погрешность косвенного однократного измерения физической величины, описываемой формулой (1.8),находится как 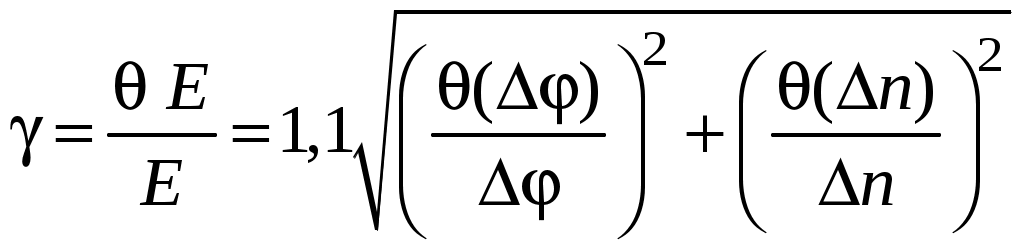 , % (1.10) , % (1.10)где 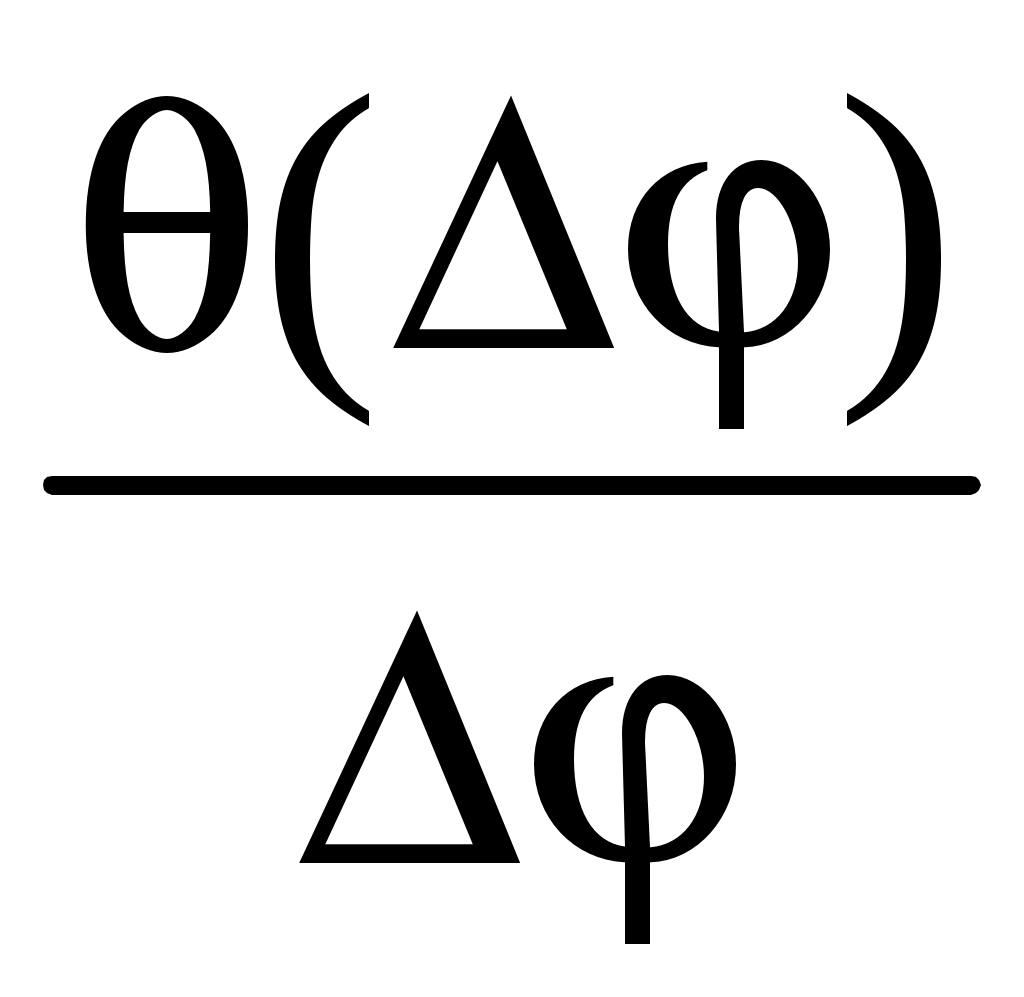 , , 2. Систематическая абсолютная погрешность находится из ее связи с относительной 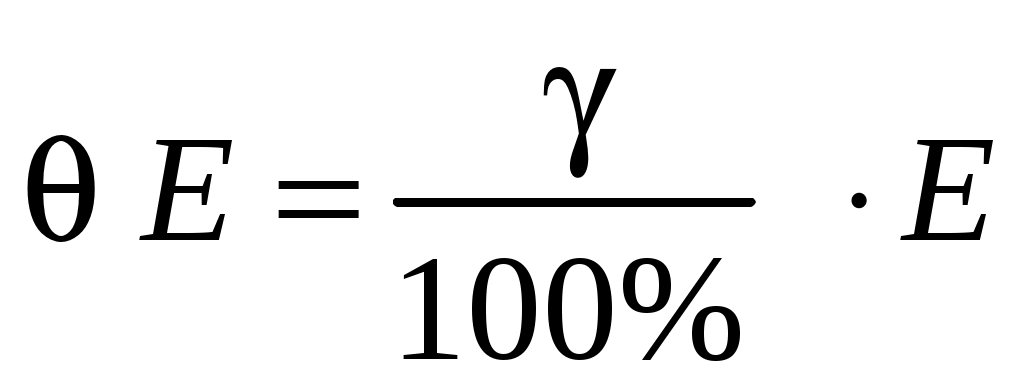 . (1.11) . (1.11)3. Оформить отчёт о выполнении работы в соответствии с прилагаемым образцом. ОТЧЁТ по лабораторной работе «Изучение электростатического поля методом моделирования» Исполнитель: студент(ка) гр.____ Цель работы: ... Краткое описание метода исследования:... Расчетные формулы: (объяснить входящие в формулы физические величины и указать единицы их измерения в системе СИ). Оборудование: ... Средства измерений и их характеристикиТаблица 1.1
Расчёты 1 Написать формулу, показать расчёт и записать результат! . E = … = … = … В/м; (1.8) 2. = … = … = … %; (1.10) 3. E = … = … = … В/м; (1.11) 4. Окончательный результат: Е = … … В/м, … Изобразить вектор напряжённости электрического поля на графике. 5. Вывод. Примечание. Графическое изображение модели электростатического поля прилагается к отчёту. |
