л.р гармоническое колебание физика. гармон кколеб. Изучение гармонических колебаний

• Название: Изучение гармонических колебаний
• Анкор: л.р гармоническое колебание физика
• Дата: 10.11.2022
• Размер: 170 Kb.
• Имя файла: гармон кколеб.doc
• Тип: Лабораторная работа; #781165

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ

БЕЛАРУСЬ

Гомельский государственный технический университет

имени П.О.Сухого

Кафедра физики

Лабораторная работа № 1-7

Начало работы

Выполнил студент гр. Э-13

Колесников П.М.

Принял преподаватель

Проневич О.И.

г. Гомель, 2001

Тема: Изучение гармонических колебаний.
Цель работы: Изучить гармоническое колебательное движение на примерах колебаний математического, физического и оборотного маятников. Используя математический и оборотный маятник, определить ускорение свободного падения.
Приборы: Универсальный маятник РМ-04, и другие приборы входящие в состав системы приборов для лаборатории «физические основы механики».
Теоретическая часть:

Гармоническим колебательным движением является движение, при котором тело движется во времени по синусоидальному или косинусоидальному закону.

Свойства гармонических колебаний: - Частота колебаний не зависит от амплитуды.

- Принцип суперпозиций.

Уравнением движения гармонического осциллятора является уравнение вида: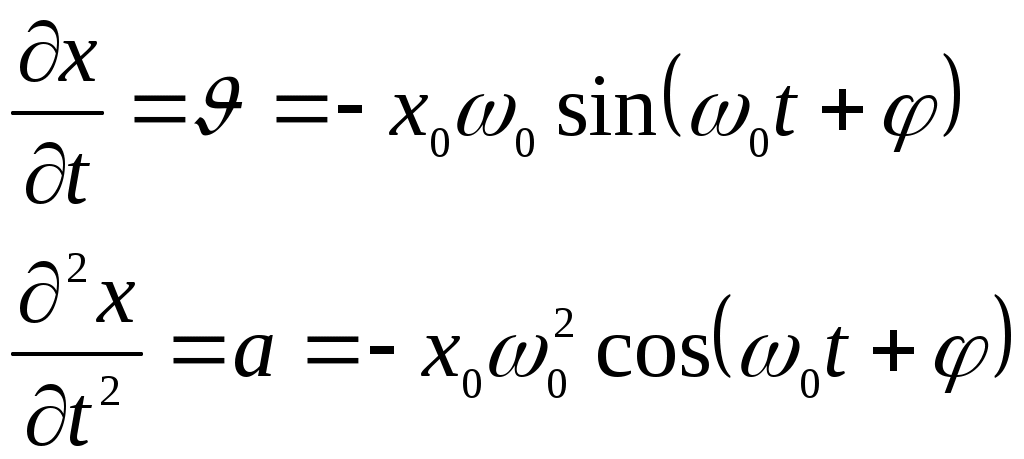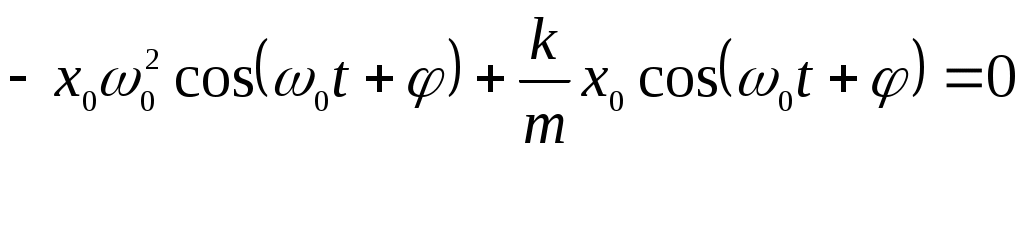

, где

, где А - амплитуда колебаний

- фаза колебаний



Частота:

Период:

Затухающие синусоидальные колебания:

, где величина - амплитуда затухающих колебаний, - коэффициент затухания , - собственная частота затухающих колебаний.

Затухающие колебания представляют собой непериодические колебания. Если 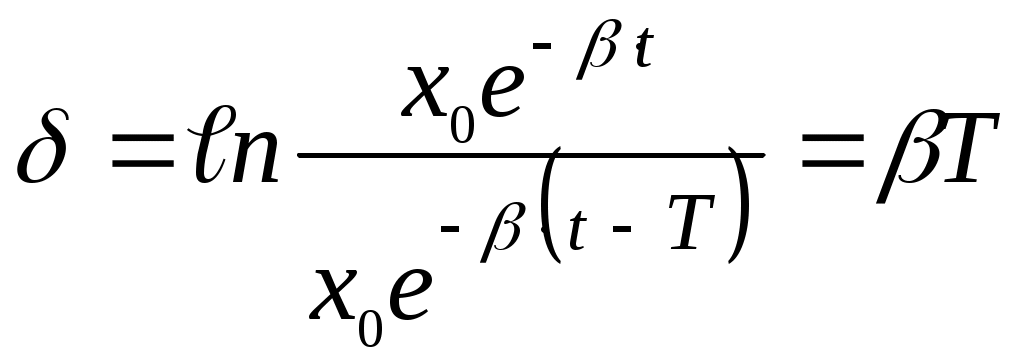, то для характеристики затухающих колебаний используют логарифмический дескремент затухания - это натуральный логарифм отношения амплитуды отстоящих друг от друга на период:



Если - такое движения системы не имеет колебательного характера и называется апериодическим.

Добротность – безразмерная величина, равная произведению на отношение энергии колебательной системы в произвольный момент времени к убыли этой энергии за промежуток времени от до



для слабо затухающих колебаний

Резонанс – явление резкого возрастания амплитуды колебаний при приближении циклической частоты возмущающей силы к значению резонансной частоты.

Физический маятник – твердое тело, имеющее возможность колебаться под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела.



Уравнение движения маятника имеет вид: , - расстояние от центра инерции маятника до оси качения (при малых колебаниях):



Циклическая частота колебаний физического маятника:



Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести (предельный случай физического маятника).

,

Приведенной длиной физического маятника называется длина математического маятника, имеющего такой же период же период колебаний:



Оборотный маятник – разновидность физического маятника:



Ход работы.

1. 
   Определение ускорения силы тяжести с помощью математического маятника:
   
   • 
     Измеряем время n=10 полных колебаний математического маятника, опыт повторяем три раза:
     

Таблица №1

	t,c	tср,c	Tср,c	g,m/c2	,m
1	12,808
2	12,807	12,809	1,281	9,625	0,4
3	12,811

• 
  Находим абсолютную и относительную погрешности измерений: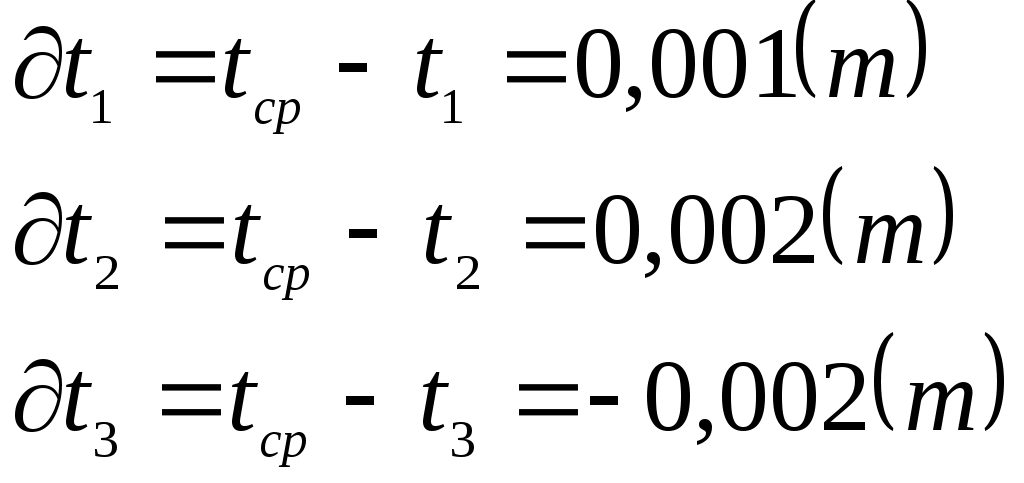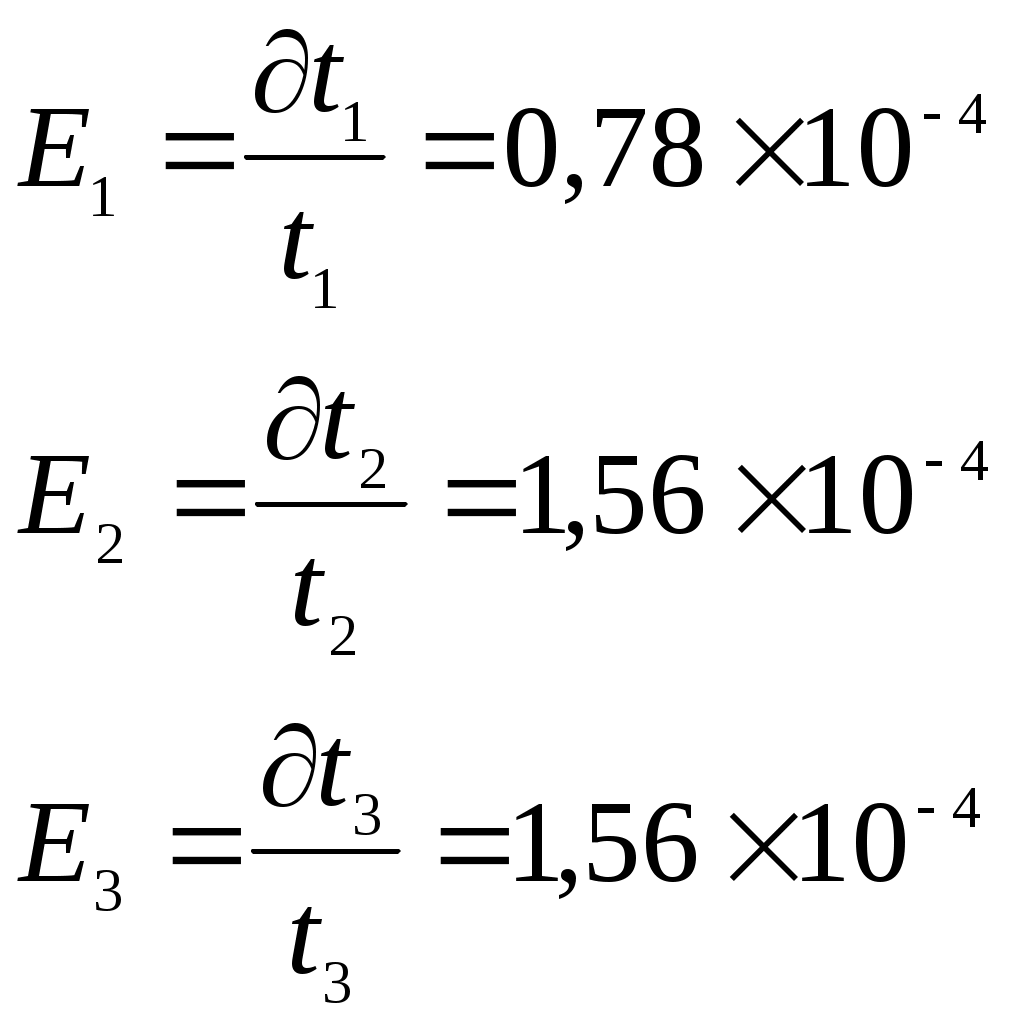
  

2. 
   Определение ускорения свободного падения с помощью оборотного маятника:
   
   • 
     измеряем время 10 полных колебаний оборотного маятника, опыт повторяем три раза: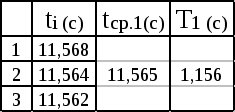
     

- Переворачиваем маятник и измеряем время 10 полных колебаний оборотного маятника, опыт повторяем три раза: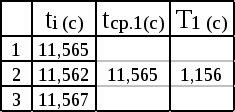

• 
  При T₁=T₂, расстояние между опорами
  
• 
  По формуле находим ускорение силы тяжести:
  

Определение момента инерции маятника:

3. 
   Собираем маятник в соответствии с требованием опыта и устанавливаем на опору.
   

Определяем момент инерции маятника при разных положениях груза по формуле:

• 
  Все измерения согласно опыта записываем в таблицу: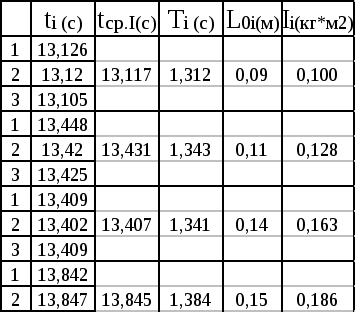
  

6. Строим график зависимости :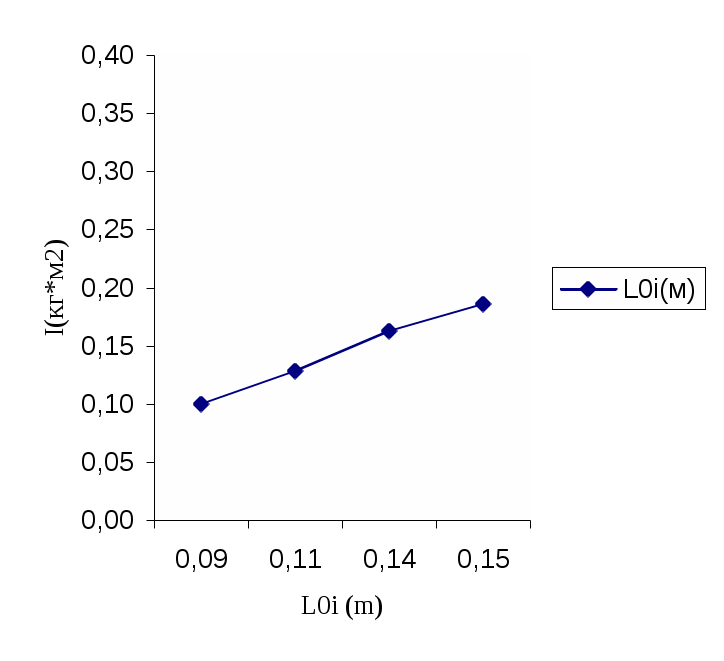



7. Вывод: Изучили гармоническое колебательное движение на примерах колебаний математического, физического и оборотного маятников. Используя математический и оборотный маятник, определили ускорение свободного падения.