изучение колебаний математического маятника. ЛР1Физика. Изучение колебаний математического маятника
 Скачать 216.56 Kb. Скачать 216.56 Kb.
|
|
Лабораторная работа №1. Тема: «Изучение колебаний математического маятника» Цель работы: Вычисление ускорения свободного падения шарика по результатам указанных измерений. Теоретическая часть: Если размеры шарика много меньше длины l нити, то шарик можно рассматривать как материальную точку; а если масса шарика много больше массы нити, то последнюю можно считать невесомой. Нить также можно считать нерастяжимой при условии, что сила тяжести шарика вызывает бесконечно малое удлинение нити. Действительно, в исходном состояние нить направлена вертикально вниз. В этом случае сила F натяжения нити и сила mg тяжести шарика совпадают с направлением нити, но противоположно направлены. Так как нить нерастяжима, то обе силы уравновешивают друг друга, то есть F = mg. Шарик находится в покое. Такое состояние маятника называется положением его равновесия. Очевидно, что траекторией движения шарика будет дуга окружности радиуса l. Такие движения называются колебаниями. Однако если наблюдать данный процесс в течение довольно короткого времени, то колебательный процесс можно признать незатухающим. maτ= - mg sin φ Здесь aτ – тангенциальное ускорение, m – масса шарика. Знак минус справа учитывает то обстоятельство, что при движении от положения равновесия вверх сила тяжести препятствует этому движению. Угловое ускорение ε шарика определяется как вторая производная по времени от угла φ, то есть 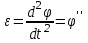 . . Такое уравнение в математике называют обыкновенным дифференциальным уравнением второго порядка. Его можно упростить, если учесть, что при малых углах φ, измеренных в радианах 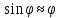 . Тогда вместо будем иметь . Тогда вместо будем иметь 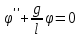 . . Уравнение описывает движение маятника. Его ещё называют уравнением гармонического осциллятора. Таким образом, видно, что изменения угла φ по времени происходит по синусоидальному закону. Величина φ0, равная максимальному углу отклонения от положения равновесия, называется амплитудой гармонических колебаний. Величина амплитуды в данном случае зависит от первоначального отклонения. Величина же 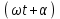 стоящая под знаком синуса называется фазой. Фаза растёт пропорционально времени. Величина стоящая под знаком синуса называется фазой. Фаза растёт пропорционально времени. Величина 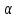 под знаком синуса называется начальной фазой, которая в рассматриваемом движении равна нулю. под знаком синуса называется начальной фазой, которая в рассматриваемом движении равна нулю.Функция синуса, определяющая характер колебательных движений, суть периодическая функция с величиной периода равного 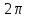 . Последнее означает, что если через T обозначить период колебаний маятника, то можно написать следующее равенство для величины фазы . Последнее означает, что если через T обозначить период колебаний маятника, то можно написать следующее равенство для величины фазы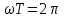 , где , где  – круговая частота. – круговая частота.Теперь с учётом для периода Т будем иметь:   Такие колебания называются изохронными. Формулу можно ещё представить так: 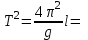 kl, kl,Функциональная зависимость  , построенная по экспериментальным точкам, позволяет определить угловой коэффициент k, через числовое значение которого ускорение g свободного падения шарика вычисляется так: , построенная по экспериментальным точкам, позволяет определить угловой коэффициент k, через числовое значение которого ускорение g свободного падения шарика вычисляется так: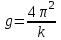 . .Кроме того, по единичным измерениям T и l ускорение g можно вычислить ещё из такого соотношения: 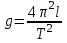 . .Порядок проведения эксперимента: Следовательно, чтобы определить диапазон значений φ0 , при которых справедливо соотношение, необходимо для нескольких значений φ0 произвести измерения, позволяющие построить зависимости  , далее из указанных функциональных зависимостей вычислить угловой коэффициент k и для выбранных углов φ0 вычислить значения g по (12), и сравнить их с общепринятым значением g = 9,8 м/с2. Те углы φ0, для которых вычисленная величина g с учётом погрешности измерений сохранит одинаковые числовые значения и определяет диапазон изохронности колебаний, реализуемых данным прибором. , далее из указанных функциональных зависимостей вычислить угловой коэффициент k и для выбранных углов φ0 вычислить значения g по (12), и сравнить их с общепринятым значением g = 9,8 м/с2. Те углы φ0, для которых вычисленная величина g с учётом погрешности измерений сохранит одинаковые числовые значения и определяет диапазон изохронности колебаний, реализуемых данным прибором.Порядок измерений таков: Выбирается конкретное значение угла φ0, на которое необходимо отклонить шарик от положения равновесия Устанавливается длина маятника, производится опыт, в процессе которого измеряется период T. Опыт производится несколько раз так, что при фиксированном угле φ0 необходимо иметь от трёх до пяти измеренных значений l и T. Предлагается сделать по пять таких серий измерений для каждого из углов φ0, в качестве которых выбираются следующие три угла: φ0 = 10о; φ0 = 20о; φ0 = 30о. По многократно измеренным значениям l и T для выбранного угла φ0 вычисляются их средние арифметические по формулам: 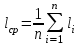 , , 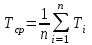 На приборе, реализующем колебательные движения маятника, имеется устройство, регулирующее длину нити. Подвижная платформа позволяет измерять длину маятника ещё одним способом. Для этого необходимо нить маятника вместе с шариком совместить с верхней плоскостью подвижной платформы. Данное же положение платформы можно зафиксировать на измерительной линейке – это будет длина нити вместе с шариком, из которой необходимо вычесть радиус шарика. Диаметр шарика необходимо измерить штангенциркулем. Период T колебаний маятника лучше определять так: измерить время t нескольких колебаний маятника и затем разделить это время на число колебаний. При этом надо иметь в виду, что под временем одного колебания подразумевается то время, в течение которого шарик из одного из крайних положений возвращается в то же положение. Для установления требуемого угла φ0 необходимо воспользоваться прямоугольной металлической пластиной, на которой из одной точки выходят несколько направляющих линий, наклонённых под различными углами к вертикальной линии, исходящей из этой точки. Эти углы можно измерить с помощью транспортира. Обработка результатов измерений: Любое из измеренных значений l и T, представленных в таблицах 1-3 не являются точными величинами, так как они измерены с определёнными погрешностями. В таких случаях в качестве точных значений указанных величин принимаются их средние арифметические, вычисляемые по формулам. Тогда под погрешностью измерения будем подразумевать модуль величины максимального отклонения всех измеренных величин от их среднего арифметического. А именно, погрешность ∆1 измерения длины маятника будем определять как ∆1 = max |li - lср|, а погрешность ∆2 - периода колебаний маятника следует вычислять так: ∆2 = max |Ti – Tср|. В формулах индекс i = 1,2,3 … пробегает все номера измерений соответствующих величин. Обработку результатов измерений будем производить на компьютере в программе Microsoft Excel и продемонстрируем технологию необходимых при этом расчётов на конкретных результатах измерений. Пусть таблица 3 заполнена следующими фактическими данными. Таблица 3.
Для каждой серии измерений необходимо по формулам вычислить lср и Tср, а затем построить зависимость Tср2 = f(lср). Для удобства введём обозначения: Tср2 = y1, lср = x1. Прежде чем перейти к указанным вычислениям построим в программе Excel таблицу 3 и заготовим формат таблицы 4, данные которой будут использованы при построении функциональной зависимости y1 = f(x1). В программе Excel таблица 3 формируется следующим образом. На Листе1 рабочей книги Excel активизируем диапазон ячеек ячейку A1:A2, объединим их и занесём в получившуюся объединённую ячейку с клавиатуры заголовок первого столбца: «n номер измерения», активизируем диапазон ячеек B1:C1, объединим их и занесём в получившуюся объединённую ячейку с клавиатуры общий заголовок второго и третьего столбца: «серия 1», активизируем ячейку B2 и занесём в неё с клавиатуры подзаголовок второго столбца таблицы 3: «l» после чего, активизируем ячейку С2 и занесём в неё с клавиатуры подзаголовок третьего столбца таблицы 3: «T». Повторим указанные действия для остальных столбцов таблицы 3. В результате выполнения вышеуказанных действий получим формат таблицы 3.  Теперь заполним полученный формат данными таблицы 3, в результате чего получим таблицу 3 в программе Excel.  Для построения формата таблицы 4 в программе Excel на Листе1 рабочей книги Excel активизируем ячейку A9 и вводим в неё с клавиатуры заголовок первого столбца: «n номер серии измерений», активизируем ячейку B9 и вводим в неё с клавиатуры заголовок второго столбца: «lср=x1». Аналогично заносим с клавиатуры заголовки третьего, четвёртого и пятого столбцов: «Tср», «Tср2=y1» и «y1 / x1» в ячейки C1, D1 и E1 соответственно. Далее, активизируем ячейку A10 и занесём в неё с клавиатуры цифру 1, в ячейку A11 цифру 2, активизируем диапазон ячеек A10:A11 и выполним автозаполнение до ячейки A14. В результате выполнения вышеуказанных действий получим таблицу 4. Таблица 4. 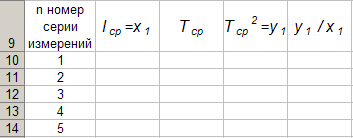 Технологию заполнения первой строки таблицы 4 продемонстрируем на обработке измерений серии 1. Для чего программируем первую формулу, получаем lср и заносим в таблицу 4. Для этого активизируем ячейку B10 и заносим с клавиатуры формулу «=СУММ(B3:B7)*(1/5)». Потом программируем вторую формулу. Для этого активизируем ячейку E2 и заносим с клавиатуры формулу «=СУММ(C3:C7)*(1/5)». Получаем Tср и возводим её в квадрат, после чего вычисляем отношение 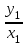 . Для этого активизируем ячейку D10 и заносим с клавиатуры формулу «=C10^2», затем активизируем ячейку E10 и заносим с клавиатуры формулу «=D10/B10». После всех этих действий первая строка таблицы 4 принимает вид: . Для этого активизируем ячейку D10 и заносим с клавиатуры формулу «=C10^2», затем активизируем ячейку E10 и заносим с клавиатуры формулу «=D10/B10». После всех этих действий первая строка таблицы 4 принимает вид: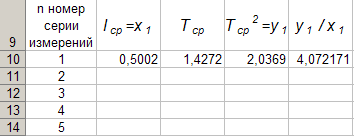 После повторения указанных расчётов для других серий Таблица 4 принимает окончательных вид: 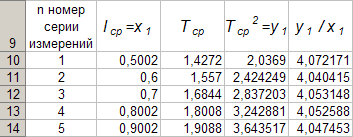 Данные таблицы 4 позволяют с помощью программы Excel построить график функциональной зависимости y1 = f(x1). Для этого активизируем диапазон ячеек D10:D14, вызовем Мастер Функций программы Excel, выберем тип диаграммы «Точечная», вид первый. Подведём курсор мыши к кнопке «Далее» и выполним однократное нажатие левой клавиши мыши. После этого перейдём на вкладку Ряд. Для этого подведём курсор мыши в вкладке «Ряд», находящейся в верхней части окна «Мастер Диаграмм» и выполним однократное нажатие ЛКМ. Далее установим курсор в поле «Значения Х» после чего подведём курсор мыши к ячейке B10, нажмём ЛКМ и не отпуская её переместим курсор мыши до ячейки B14 после чего отпустим ЛКМ. В результате в поле «Значения Х» будет записана формула «=Лист1!$B$10:$B$14». Теперь подведём курсор мыши к кнопке «Далее» и выполним подряд два нажатия ЛКМ после чего переместим курсор мыши на кнопку «Готово» и выполним однократное нажатие ЛКМ. На Листе1 рабочей книги Excel появится график функциональной зависимости y1 = f(x1). Активизируем строку 10 и добавим новую строку, после чего занесём с клавиатуры в ячейки A10:E10 цифру «0». Далее, подведём курсор мыши к любой точке графика и выполним однократное нажатие ЛКМ. Увеличим диапазон данных графика, для чего подведём курсор мыши к границе диапазона значений y1 и передвинем маркер, расположенный в правом верхнем углу границы до ячейки D10. Аналогично поступим с диапазоном x1. 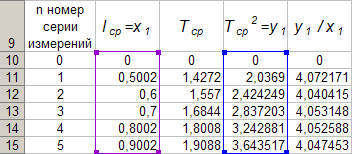 Теперь подведём курсор мыши к любой точке графика и выполним однократное нажатие правой клавиши мыши. В появившемся контекстном меню подведём курсор мыши к команде «Добавить линию тренда» и выполним однократное нажатие ЛКМ. Рисунок 1 иллюстрирует результат указанных построений. 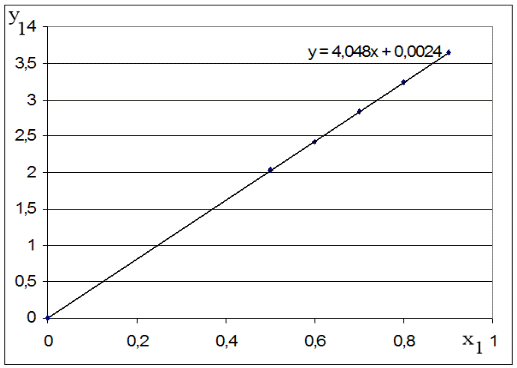 Рис 1. Из рисунка 1 следует, что зависимость y1 = f(x1) имеет линейный характер и описывается уравнением y1 = 4,048 x1 + 0,0024. Уравнение показывает, что угловой коэффициент k из уравнения оказывается равным: k = 4,0493. Если это значение k подставить в формулу, то получим величину ускорения свободного падения. Угловой коэффициент k в уравнении можно вычислить и из данных таблицы 4 по формуле 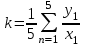 . .Для этого активизируем ячейку A17 и занесём в неё с клавиатуры формулу «=СУММ(E11:E15)*(1/5)» 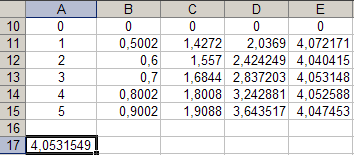 получим k = 4,053, т.е. число близкое к числу k, полученному из графика, изображённого на рисунке 1. Очевидно, что число 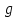 , полученное по формуле с использованием величины k из уравнения будет обладать некоторой погрешностью. , полученное по формуле с использованием величины k из уравнения будет обладать некоторой погрешностью.Чтобы вычислить эту погрешность вернёмся к данным таблиц 3 и 4. Вначале в программе Excel создадим формат новой таблицы 5. Для чего на Листе1 рабочей книги Excel активизируем ячейку A19 и занесём в неё с клавиатуры заголовок первого столбца: «n номер серии измерений», активизируем ячейку B19 и занесём в неё с клавиатуры заголовок второго столбца: «∆1». Аналогично занесём с клавиатуры заголовки третьего столбца: «∆2» в ячейку C19. Далее, активизируем ячейку A20 и занесём в неё с клавиатуры цифру 1, в ячейку A21 цифру 2, активизируем диапазон ячеек A20:A21 и выполним автозаполнение до ячейки A26. В результате выполнения вышеуказанных действий получим таблицу 5. Таблица 5. 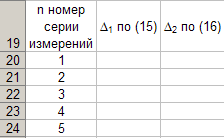 При программировании формул и необходимо li и Ti, каждой серии измерений брать из таблицы 3, а lср и Tср из данных таблицы 4. Чтобы вычислить ∆1 для первой серии измерений необходимо активизировать ячейку M3 и занести в неё с клавиатуры формулу «=ABS(B3-B$11))» после чего выполним автозаполнение до ячейки M7. Теперь в ячейку B20 занесём с клавиатуры формулу «=МАКС(M3:M7)». Для вычисления ∆2 по данным той же серии необходимо активизировать ячейку N3 и занести в неё с клавиатуры формулу «=ABS(C3-C$11)» после чего выполним автозаполнение до ячейки N7. Теперь в ячейку C20 занесём с клавиатуры формулу «=МАКС(N3:N7)». В результате таблица 5 принимает вид: 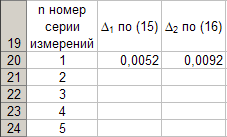 После выполнения расчётов для данных других серий измерений таблица 5 принимает вид: 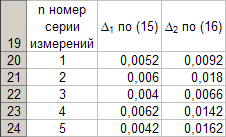 Из данных таблицы 5 очевидно, что для каждой серии измерений точные значения длины l маятника и периода T колебаний маятника определяются такl = lср ± ∆1, T = Tср ± ∆2. При этом оказывается, что ∆1 и ∆2 различны для каждой из длин маятника. Из формул следует, что прямая линия рисунка 1 проведена с погрешностью и в её окрестности имеет место так называемый разброс экспериментальных данных. Чтобы учесть разброс опытных данных, вычислим ещё две функциональные зависимости: (Tср + ∆2)2 = f(lср + ∆1), (Tср - ∆2)2 = f(lср - ∆1). Для вычисления зависимости введём новые обозначения: x2 = (lср + ∆1), y2 = (Tср + ∆2)2. Прежде чем приступить к вычислениям по формулам и образуем формат новой таблицы 6 с помощью программы Excel, по указанному ранее алгоритму, тогда получим: Таблица 6.  При вычислении x2 и y2 по (22) и (23) необходимо пользоваться данными таблиц 4 и 5. Вначале вычисляем x2 и полученные числа заносим таблицу 6. Для этого активизируем ячейку B27 и занесём в неё с клавиатуры формулу «=B11+B20». Затем вычисляем y2 для этого активизируем ячейку C27 и занесём в неё с клавиатуры формулу «=(C11+C20)^2». Теперь активизируем диапазон ячеек B27:C27 и выполним автозаполнение до ячейки C31. После чего таблица 6 заполнится следующими данными: 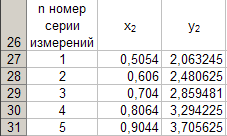 По данным таблицы 6 строим график зависимости y2 = y2(x2) (см. рис. 2) по описанной ранее технологии. 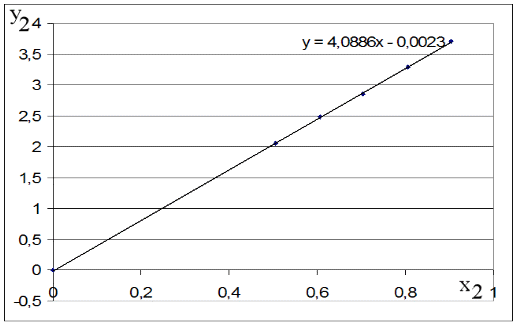 Из рисунка 2 видно, что зависимость y2 = y2(x2) определяется уравнением y2 = 4,0886 x2 – 0,0023. Переходим к вычислению функциональной зависимости. Для этого введём две вспомогательные формулы: x3 = lср - ∆1, y3 = (Tср - ∆2)2. Вычисление по этим формулам производится по данным таблиц 1 и 2, а результаты указанных вычислений заносятся в таблицу 7. Вначале вычисляем x3. Для этого активизируем ячейку B34 и занесём в неё с клавиатуры формулу «=B11-B20». Затем вычисляем y3 для этого активизируем ячейку C34 и занесём в неё с клавиатуры формулу «=(C11-C20)^2». Теперь активизируем диапазон ячеек B34:C34 и выполним автозаполнение до ячейки C38. Данные этой таблицы оказываются следующими: 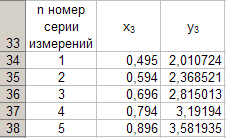 Функциональная зависимость y3 = y3(x3), построенная по данным таблицы 7 указана на рисунке 3.  Из рисунка 6 следует, что y3 = 4,0073 x3 + 0,0071. Значения углового коэффициента k по данным уравнений (17), (24), (27) заносим в таблицу 8. 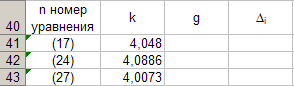 Программируем формулу и вычисляем g, соответствующее каждому значению k. Заносим полученные значения g в таблицу 8. Для этого активизируем ячейку C41 и занесём в неё с клавиатуры формулу «=(4*ПИ()^2)/B41». После этого выполним автозаполнения до ячейки C43. 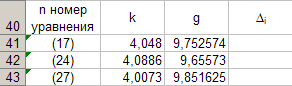 Теперь вычисляем среднее значение g по формуле 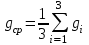 Для этого активизируем ячейку C45 и занесём в неё с клавиатуры формулу «=(1/3)*СУММ(C41:C43)». 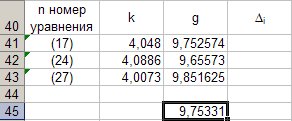 Оно оказывается равным 9,75331, которое принимаем за точное значением. Погрешность определения данного значения g вычисляем по формуле: Δ3 = max |gi – gср| = max |Δi|. Для этого активизируем ячейку D41 и занесём в неё с клавиатуры формулу «=ABS(C41-C$45)». После этого выполним автозаполнения до ячейки D43. 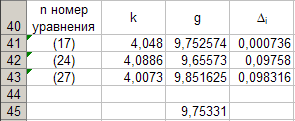 Вычисляем Δi и заносим в таблицу 8. Для этого активизируем ячейку D45 и занесём в неё с клавиатуры формулу «=МАКС(D41:D43)». 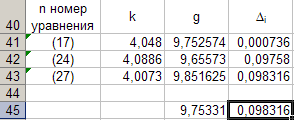 Из данных таблицы 8 следует, что Δ3 = 0,098316. Таким образом, ускорение g свободного падения, полученное на данном приборе, в результате косвенных измерений оказалось равным g = 9,7533 ± 0,0983. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
