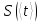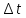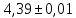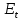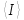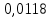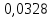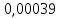Лабораторная работа №2. Изучение вращательного движения с помощью маятника Максвелла
 Скачать 131.27 Kb. Скачать 131.27 Kb.
|
|
Лабораторная работа №2 Тема: "Изучение вращательного движения с помощью маятника Максвелла". Цель работы: Экспериментальная проверка основного закона динамики вращательного движения. Определение момента инерции тела относительно оси, проходящей через центр масс тела.
1. Масса маятника 
2. Масса маятника 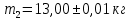
Расчёты производятся для каждой из масс m1 и m2 по отдельности, и для каждой массы заполняется своя таблица расчётов. Последующие пункты проделаны для каждой массы по отдельности. 1. Масса маятника 
1. Вычисляем среднее значение времени <t>. 2. Найдем отклонения 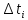 каждого из пяти измерений каждого из пяти измерений 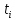 от среднего значения времени от среднего значения времени 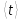 . .3. Возведем в квадрат каждое отклонение 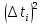 и просуммируем квадраты отклонений и просуммируем квадраты отклонений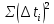 . .4. Рассчитаем среднее квадратичное отклонение S, применив для его расчёта формулу для выборочной оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей  Буквой 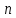 обозначено число измерений, в нашем случае обозначено число измерений, в нашем случае 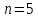 . .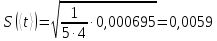 5. Умножив вычисленное значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени: 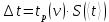 , ,где 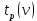 – коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы – коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы 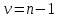 . Для . Для 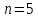 измерений при доверительной вероятности измерений при доверительной вероятности 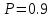 из таблицы коэффициентов Стьюдента находим из таблицы коэффициентов Стьюдента находим . .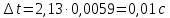 , ,6. Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается. Тогда результат измерения времени t запишем в виде: 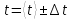 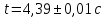 7. Произведем расчет относительной погрешности в определении времени Et (в процентах) по формуле 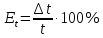 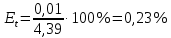 8. Вычислим момент инерции маятника по формуле 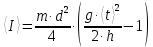 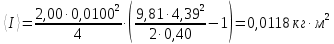 9. Рассчитаем относительную 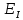 и абсолютную и абсолютную 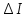 погрешности соответственно по формулам погрешности соответственно по формулам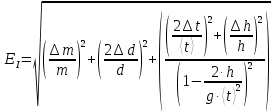 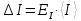 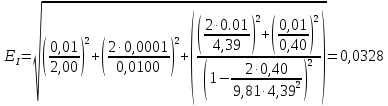 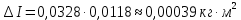 10. Представим конечный результат момента инерции в стандартной форме. 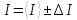 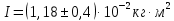 2. Массамаятника 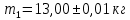
1. Вычисляем среднее значение времени <t>. 2. Найдем отклонения 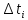 каждого из пяти измерений каждого из пяти измерений 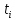 от среднего значения времени от среднего значения времени 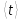 . .3. Возведем в квадрат каждое отклонение 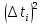 и просуммируем квадраты отклонений и просуммируем квадраты отклонений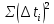 . .4. Рассчитаем среднее квадратичное отклонение S, применив для его расчёта формулу для выборочной оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей  Буквой 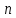 обозначено число измерений, в нашем случае обозначено число измерений, в нашем случае 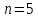 . .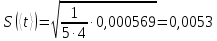 5. Умножив вычисленное значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени: 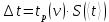 , ,где 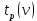 – коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы – коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы 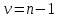 . Для . Для 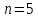 измерений при доверительной вероятности измерений при доверительной вероятности 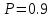 из таблицы коэффициентов Стьюдента находим из таблицы коэффициентов Стьюдента находим . .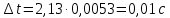 , ,6. Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается. Тогда результат измерения времени t запишем в виде: 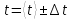 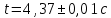 7. Произведем расчет относительной погрешности в определении времени Et (в процентах) по формуле 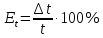 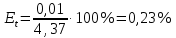 8. Вычислим момент инерции маятника по формуле 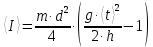  9. Рассчитаем относительную 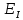 и абсолютную и абсолютную 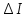 погрешности соответственно по формулам погрешности соответственно по формулам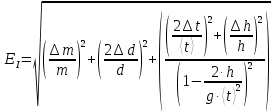 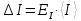 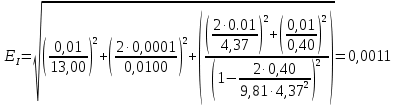  10. Представим конечный результат момента инерции в стандартной форме. 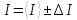 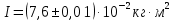   | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||