|
|
MATEM шпор 2. Ж f(x)f(x1
қисық
$$$536Қисық теңдеуімен берілген. теңдеуімен берілген.  -ті табыңыз: Ж: ctgt\2 -ті табыңыз: Ж: ctgt\2
$$$ 537Қисық теңдеуімен берілген. теңдеуімен берілген.  -ті табыңыз: Ж: 3t2+1\2t -ті табыңыз: Ж: 3t2+1\2t
$$$ 538Қисық теңдеуімен берілген. теңдеуімен берілген.  -ті табыңыз: Ж: 3\2et -ті табыңыз: Ж: 3\2et
$$$ 539Қисық теңдеуімен берілген. теңдеуімен берілген.  -ті табыңыз: Ж: t2-1\2t -ті табыңыз: Ж: t2-1\2t
$$$ 540 Ж: Ж: 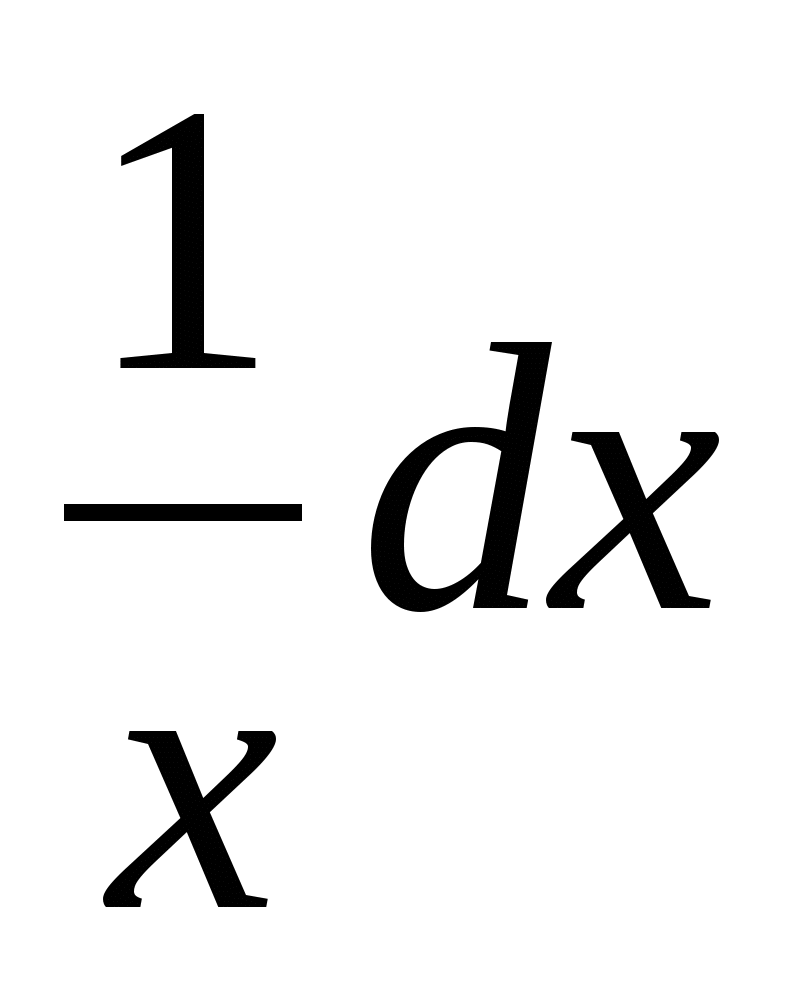
$$$ 541 Ж: 4dx Ж: 4dx
$$$ 542Лопиталь ережесі бойынша шегін тап  Ж: Ж: 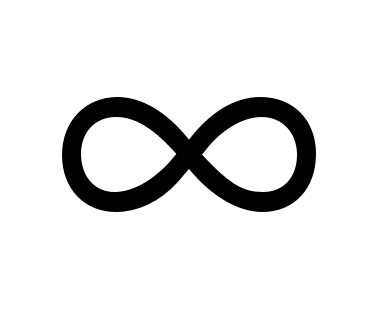
$$$ 543Лопиталь ережесі бойынша шегін тап  Ж: 2 Ж: 2
$$$ 544 көбейтіндісінің туындысының формуласын көрсет Ж: f’g+fg’ көбейтіндісінің туындысының формуласын көрсет Ж: f’g+fg’
$$$ 545 туындысының формуласын көрсетіңіз Ж: f’(x)±g’(x) туындысының формуласын көрсетіңіз Ж: f’(x)±g’(x)
$$$ 546
 туындысының формуласын көрсетіңіз: туындысының формуласын көрсетіңіз: 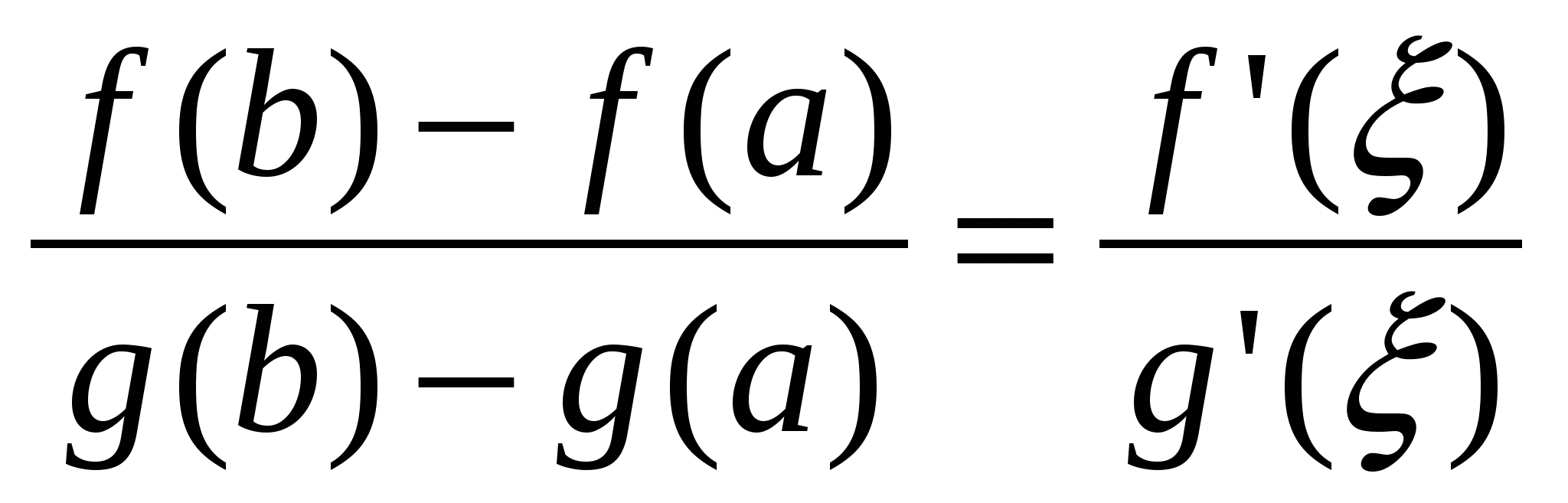
$$$ 547 туындысының формуласын көрсетіңіз: Ж: cf’(x), c=const туындысының формуласын көрсетіңіз: Ж: cf’(x), c=const
$$$ 548 функциясының функциясының  табыңыз: Ж: 2sinxcosx табыңыз: Ж: 2sinxcosx
$$$ 549 функциясының функциясының  табыңыз: Ж: 34\(5x+8)2 табыңыз: Ж: 34\(5x+8)2
$$$ 550 функциясының функциясының  табыңыз: Ж: 16(2x-7)7 табыңыз: Ж: 16(2x-7)7
ИНТЕГРАЛ
$$$ 551 интегралын табыңыз: Ж: sinx-sin3x\3 интегралын табыңыз: Ж: sinx-sin3x\3
$$$ 552 Ж: F(x)+C Ж: F(x)+C
$$$ 553 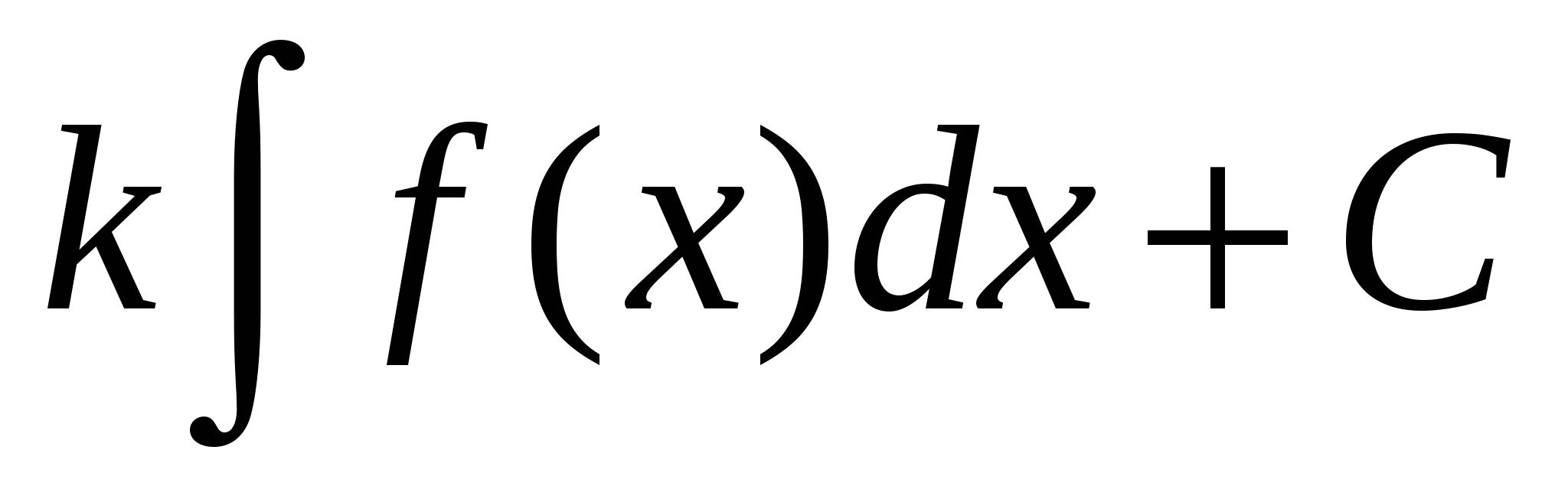
$$$ 554 Ж: Ж: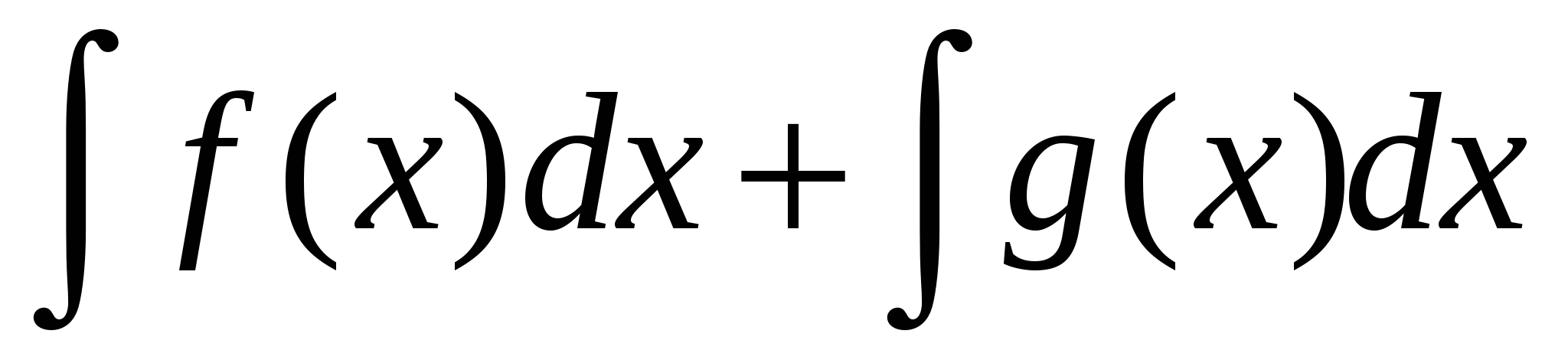
$$$ 555
Егер  болса, онда болса, онда  Ж:1\a F(ax)+C Ж:1\a F(ax)+C
$$$ 556
Егер  болса, онда болса, онда  Ж:F(x+b)+C Ж:F(x+b)+C
$$$ 557
Егер  болса, онда болса, онда  Ж: 1\a F(ax+b)+C Ж: 1\a F(ax+b)+C
$$$ 558
 Ж: f(x) Ж: f(x)
$$$ 559
Егер  болса, онда болса, онда  Ж: xm+1\m+1 Ж: xm+1\m+1
$$$ 560
Егер  , ,  болса, онда болса, онда  Ж: ax\lna+C Ж: ax\lna+C
$$$ 561 Ж: Ж: 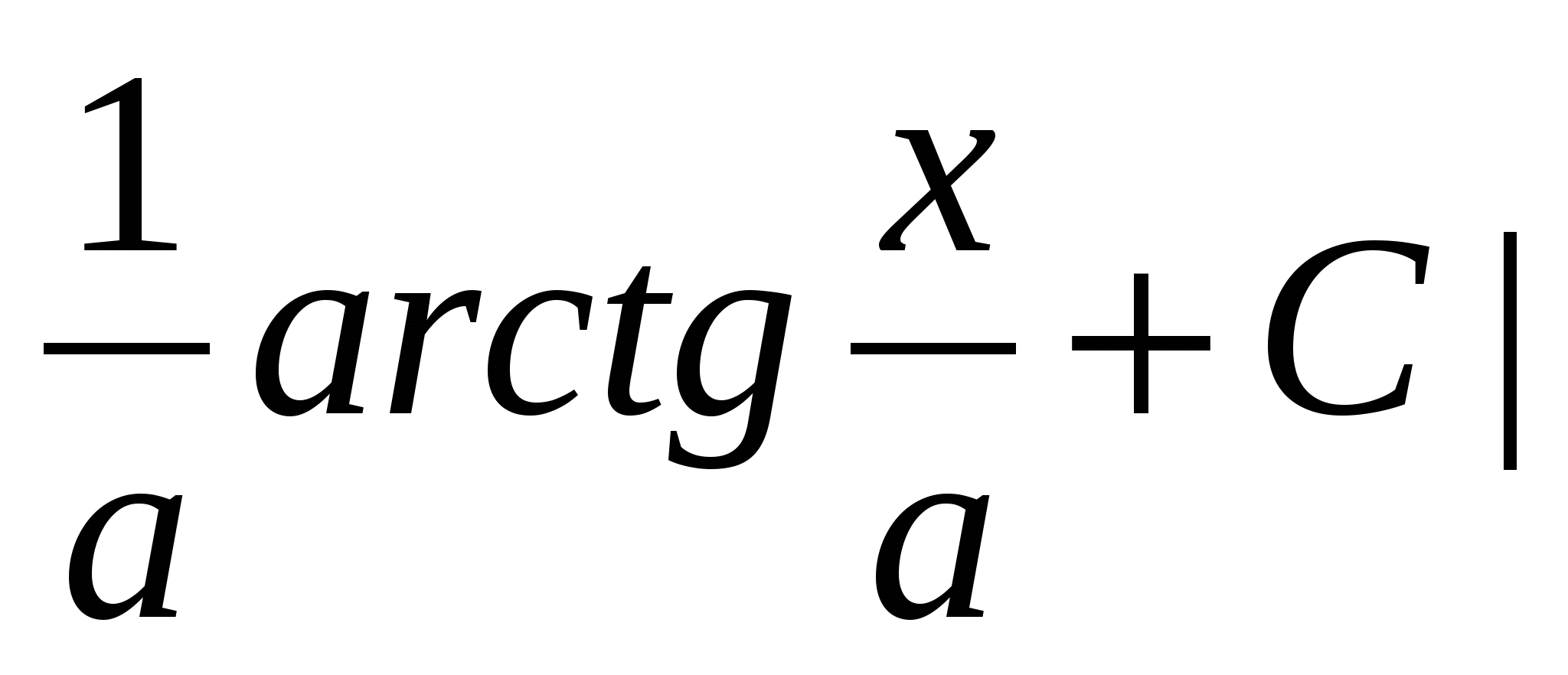
$$$ 562
Егер  болса, онда болса, онда  Ж: Ж: 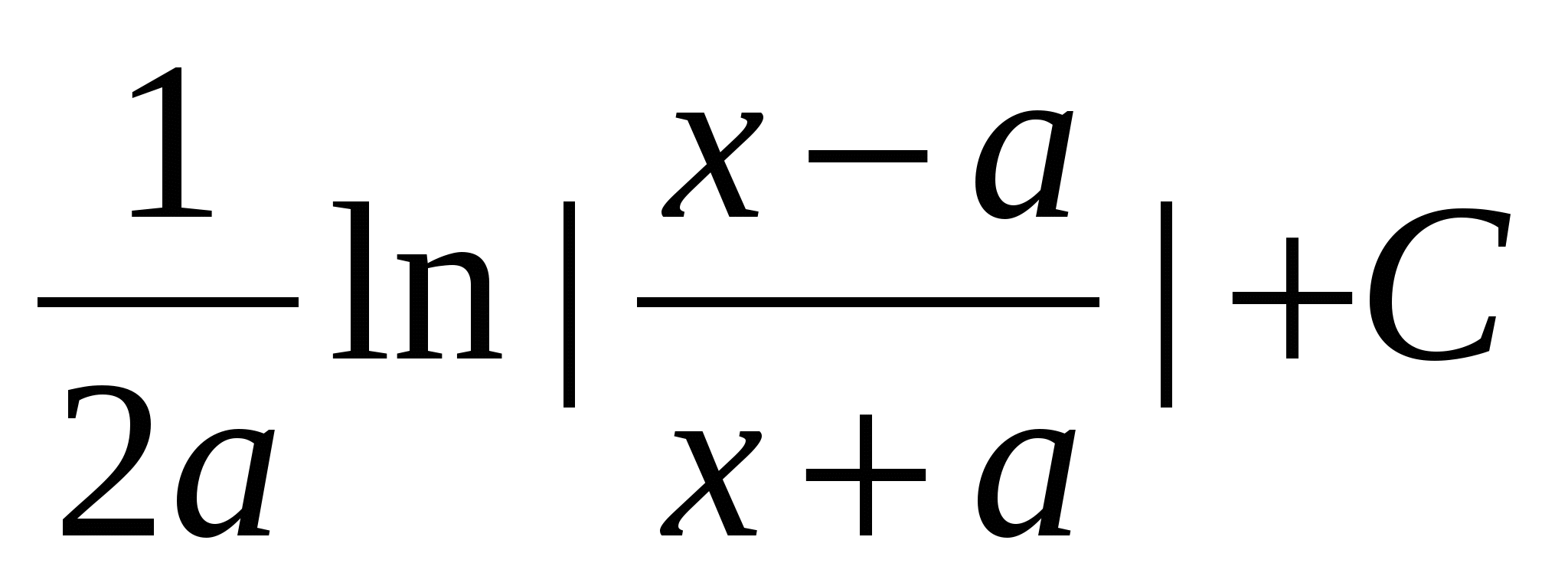
$$$ 563
Егер  болса, онда болса, онда  Ж: arcsin x\a+C Ж: arcsin x\a+C
$$$ 564
Егер  - дифференциалданатын функциялар болса, онда - дифференциалданатын функциялар болса, онда  Ж: Ж: 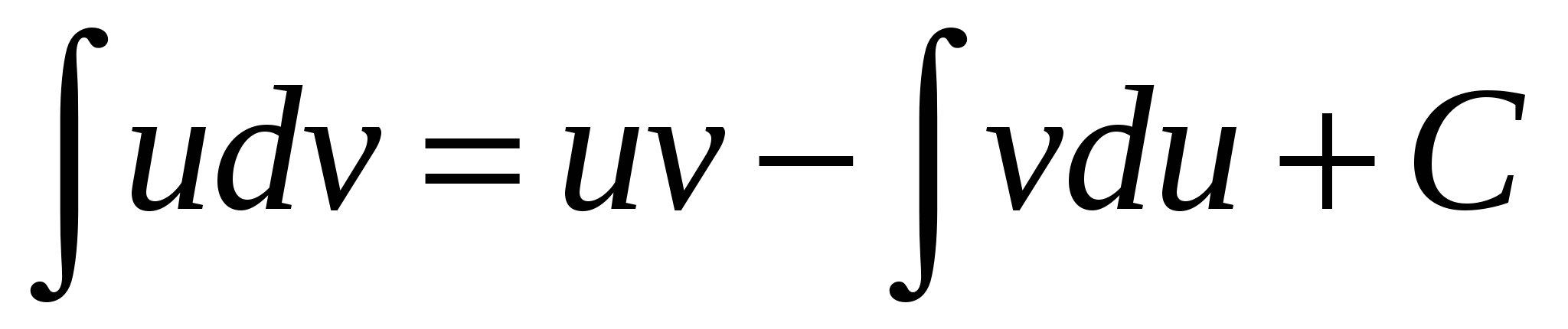
$$$ 565 Ж: tgx+c Ж: tgx+c
$$$ 566 Ж: -ctgx+C Ж: -ctgx+C
$$$ 567 Ж: Ж: 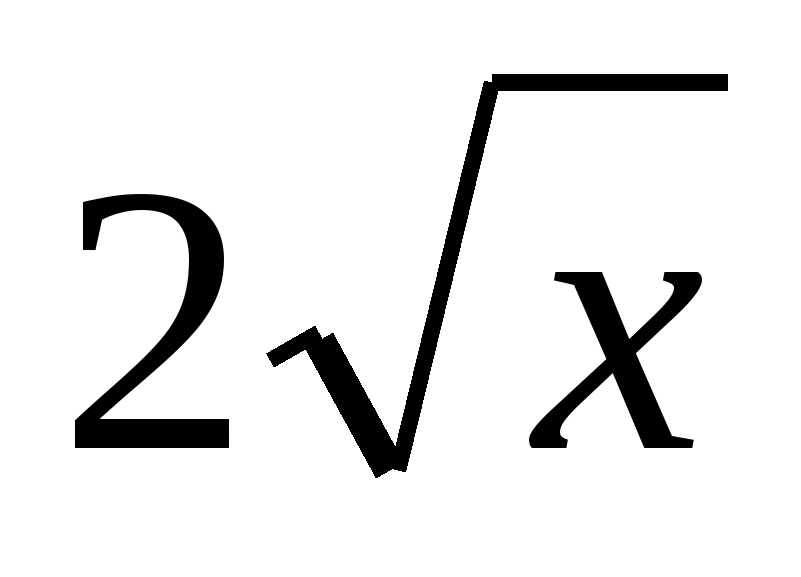 +C +C
$$$ 568 Ж: ln|x|+C Ж: ln|x|+C
$$$ 569 Ж: Ж: 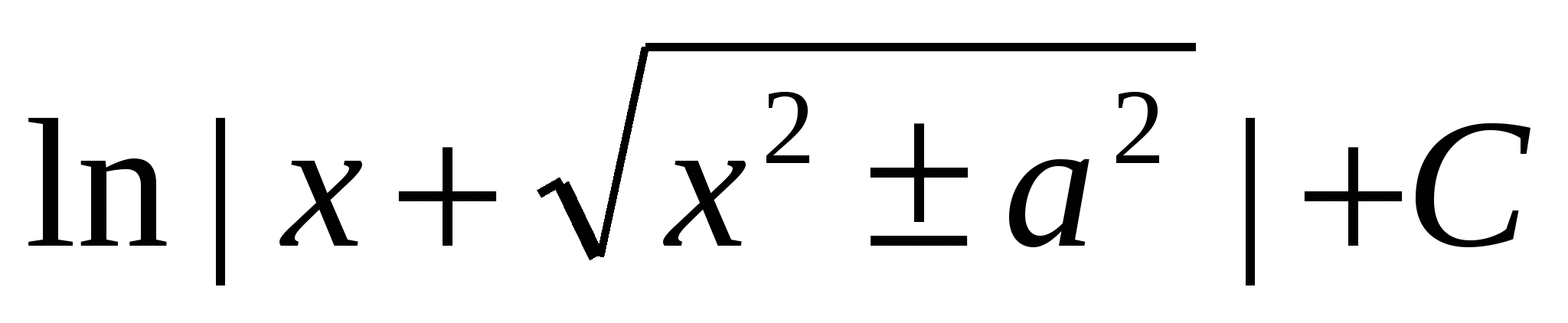
$$$ 570
 кесіндісіндегі кесіндісіндегі  функциясының анықталған интегралы функциясының анықталған интегралы  Ж: Ж: 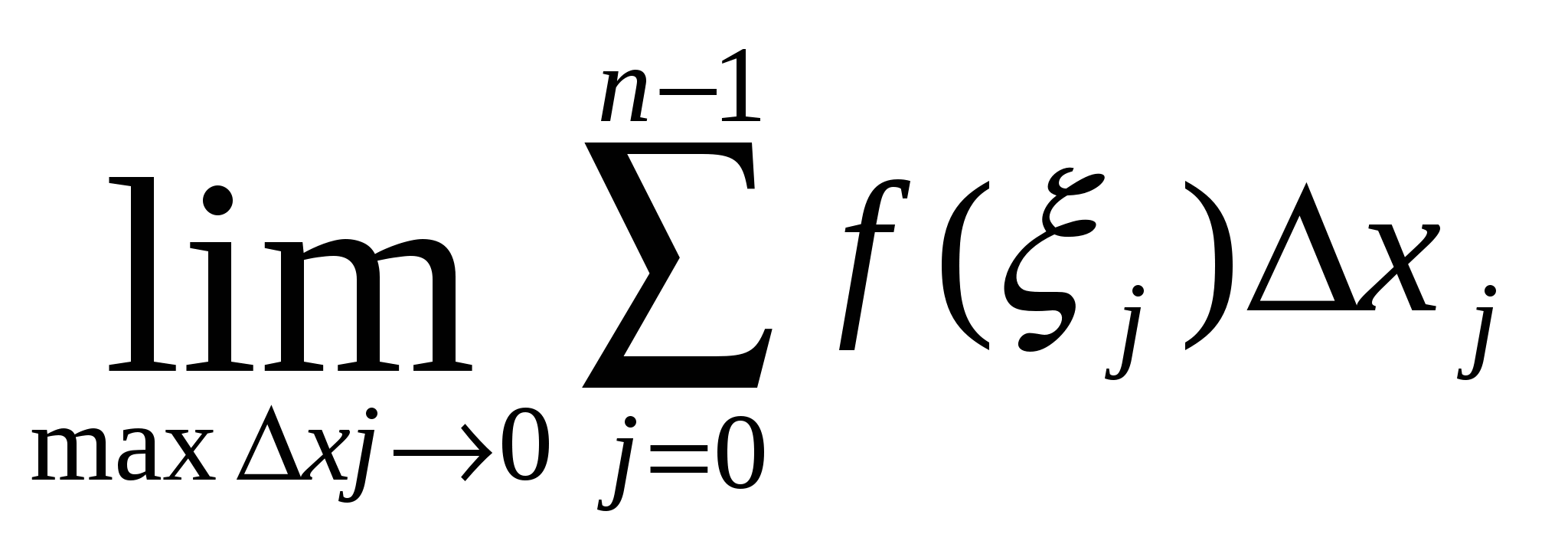 j=0,..,n-1 j=0,..,n-1
$$$ 571
 анықталмаған интегралын есептеңіз: Ж: -1\2 cos(2x+3)+C анықталмаған интегралын есептеңіз: Ж: -1\2 cos(2x+3)+C
$$$ 572
Егер  функциясы функциясы  кесіндісінде интегралданса және кесіндісінде интегралданса және  теңсіздігі орындалса, онда теңсіздігі орындалса, онда  Ж: Ж: 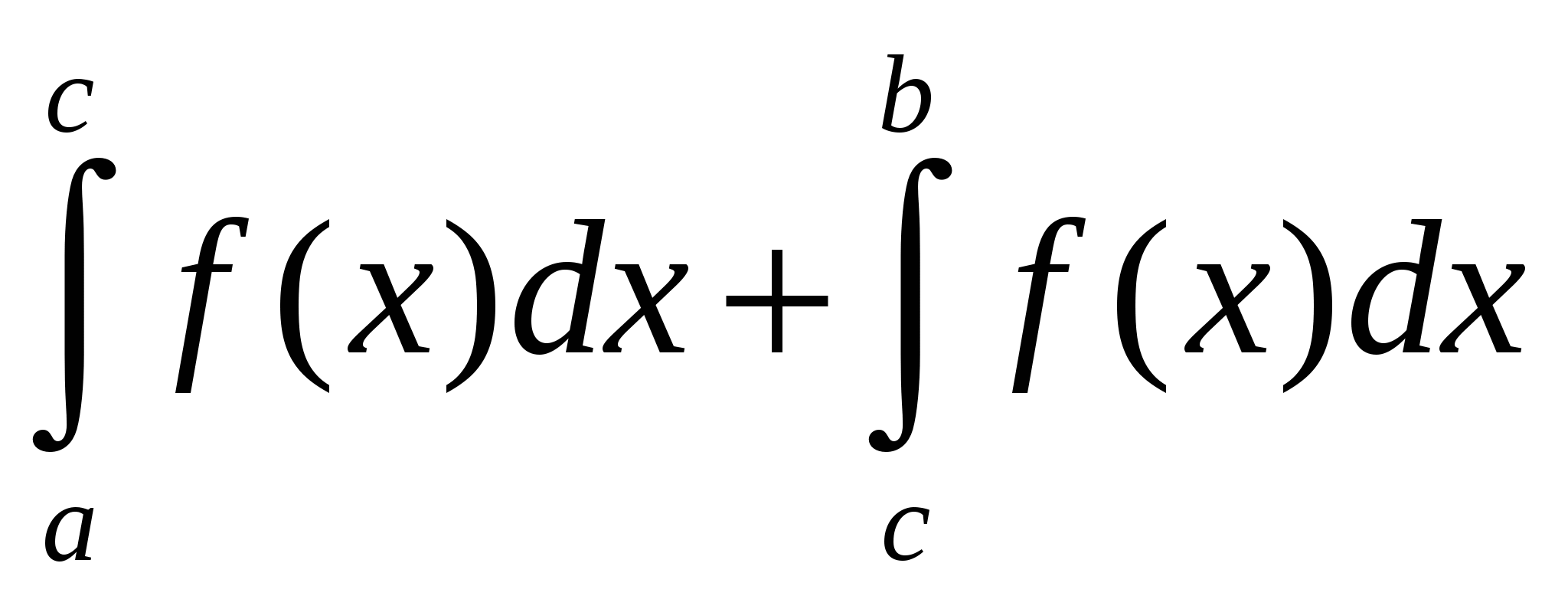
$$$ 573
Егер  , ,  функциялары функциялары  кесіндісінде интегралданса және кесіндісінде интегралданса және  , онда Ж: , онда Ж: 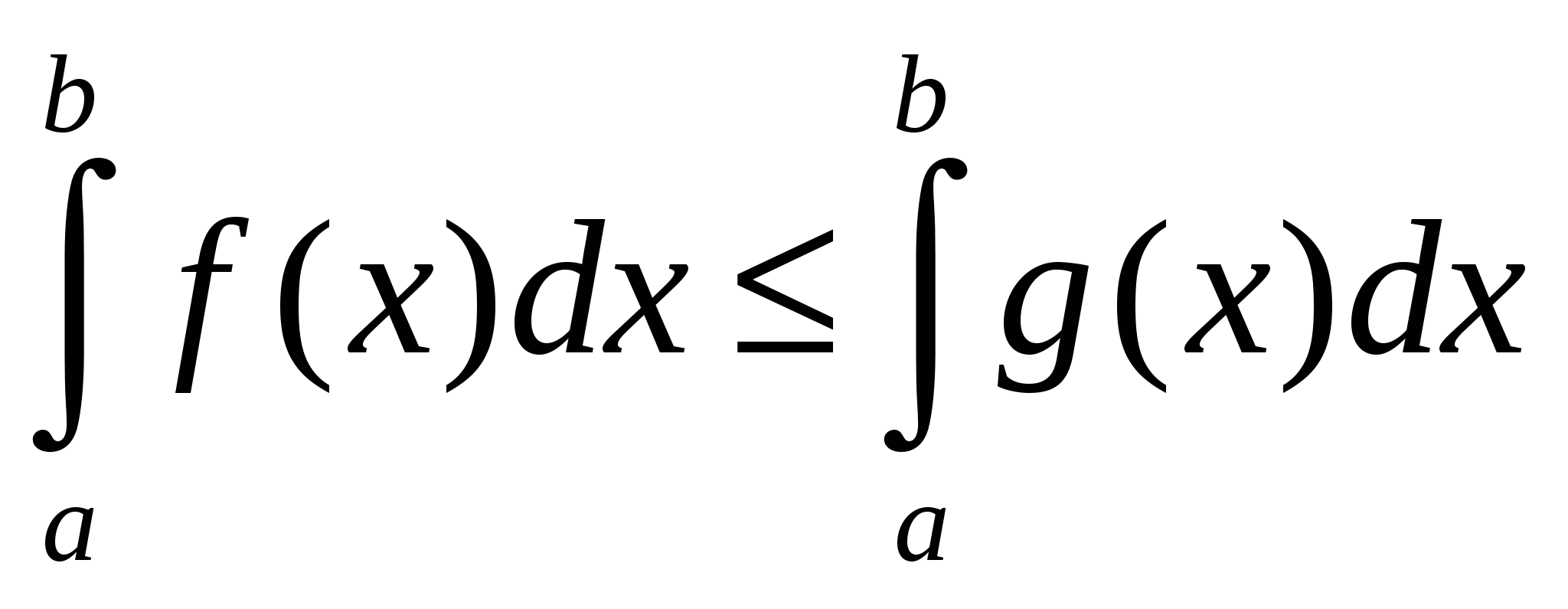
$$$ 574
Егер  функциясы функциясы  кесіндісінде үзіліссіз болса және кесіндісінде үзіліссіз болса және  оның қайсыбір алғашқы функциясы болса, онда оның қайсыбір алғашқы функциясы болса, онда  Ж: F(b)-F(a) Ж: F(b)-F(a)
$$$ 575
Егер  функциясы жұп болса, онда функциясы жұп болса, онда  Ж:2 Ж:2
$$$ 576
Егер  функциясы тақ болса, онда функциясы тақ болса, онда  Ж:0 Ж:0
$$$ 5771-ші текті меншіксіз интеграл  Ж: Ж: 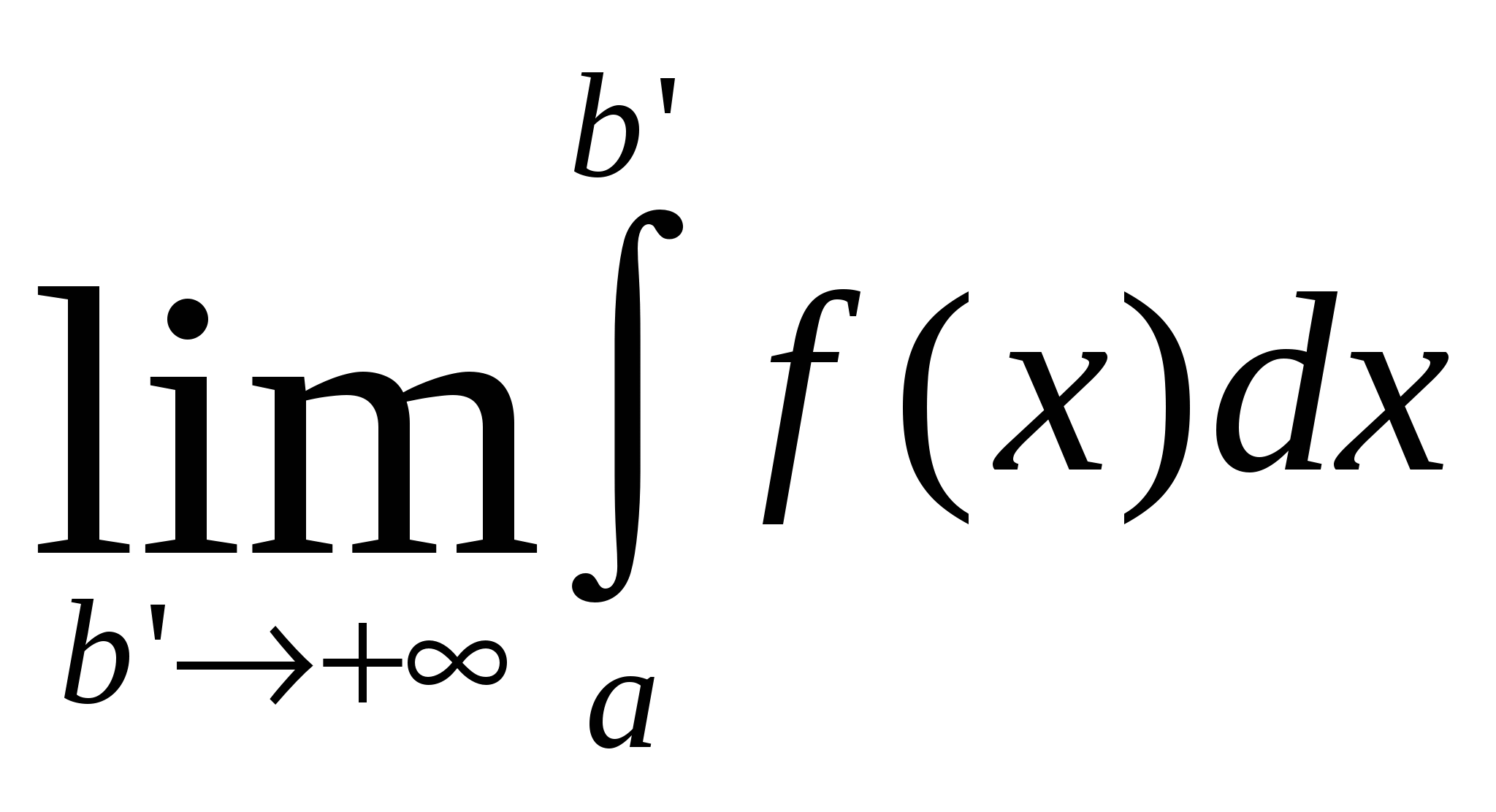
$$$ 578
Егер  кесіндісінде параметрлік теңдеумен берілген кесіндісінде параметрлік теңдеумен берілген  қисығында қисығында  , ,  функциялары үзіліссіз болса, онда функциялары үзіліссіз болса, онда  Ж: Ж: 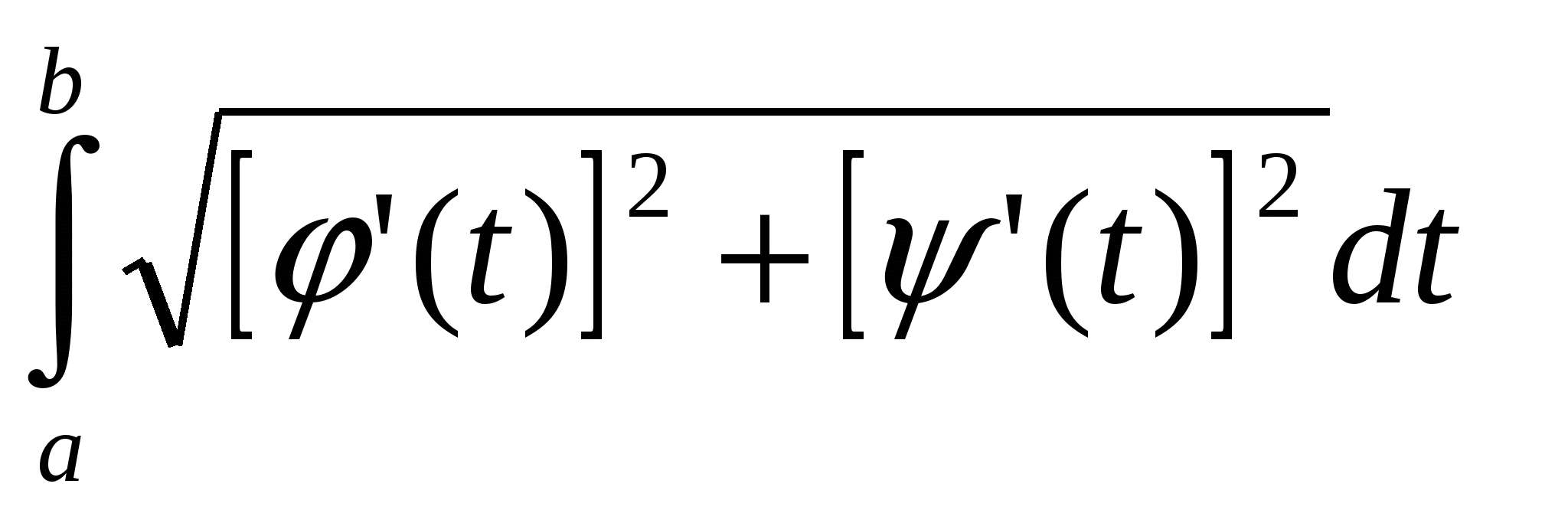
$$$ 579
Егер  қисығы қисығы  теңдеуімен берілсе, онда теңдеуімен берілсе, онда  Ж: Ж: 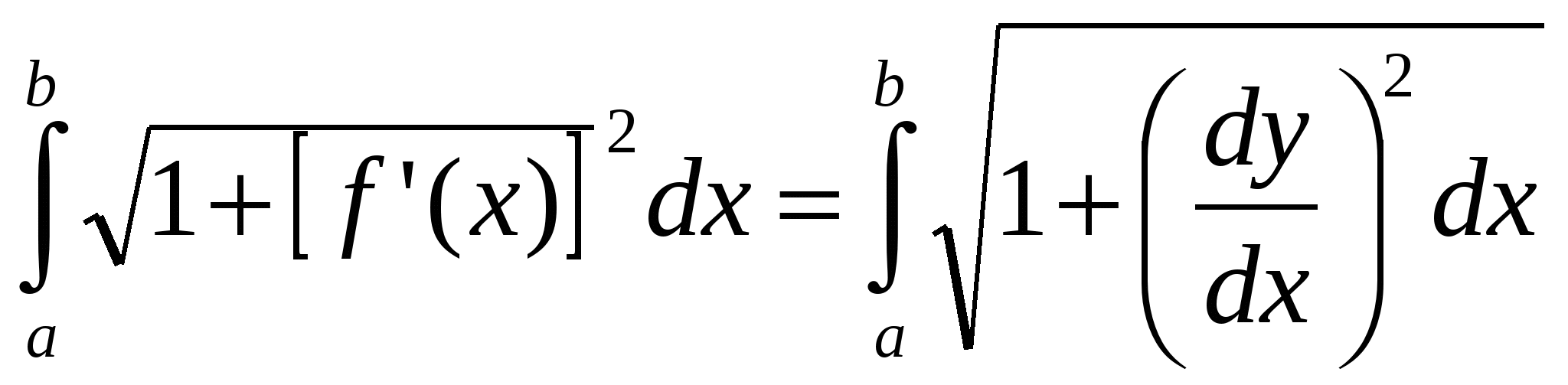
$$$ 580
Егер  қисығы поляр координат жүйесінде қисығы поляр координат жүйесінде  , ,  теңдеуімен берілсе, онда теңдеуімен берілсе, онда  Ж: Ж: 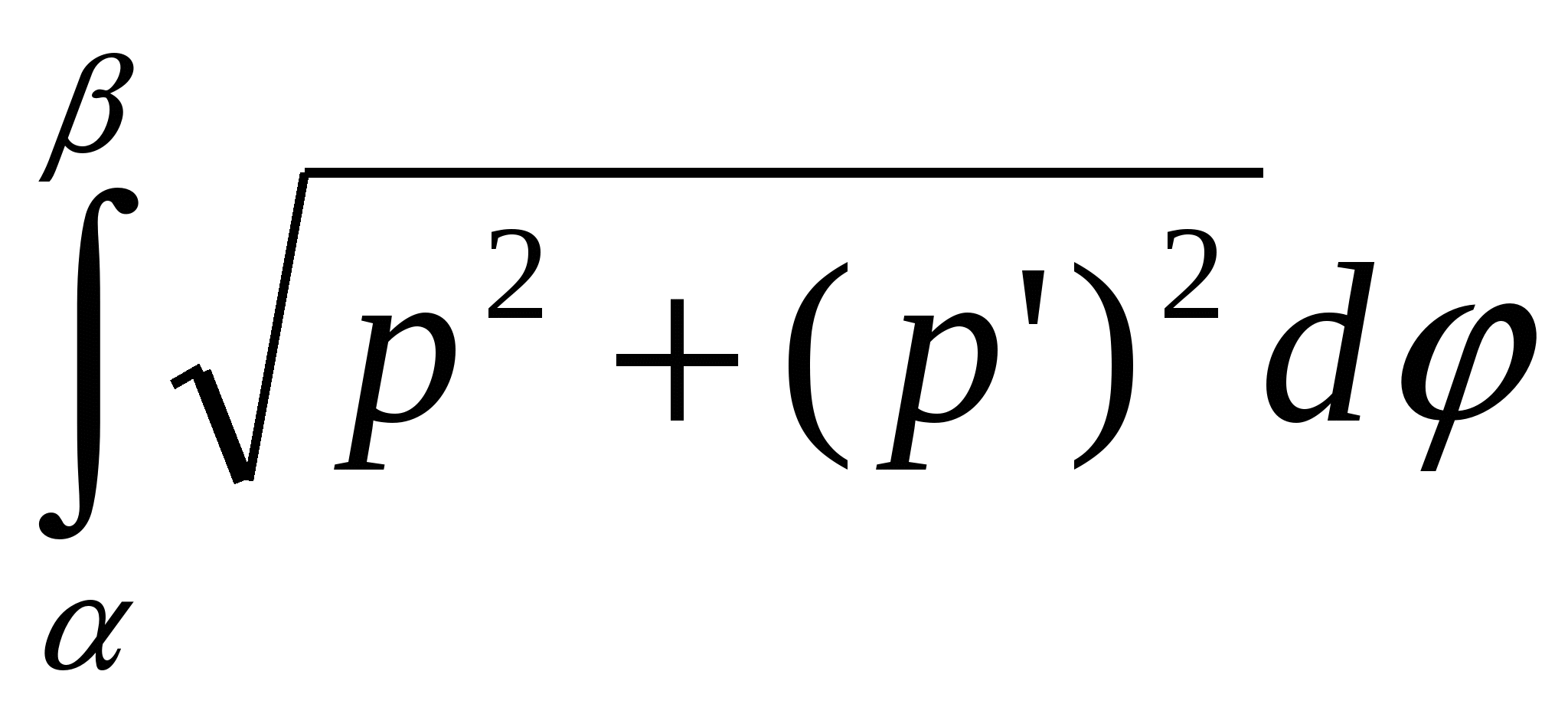
$$$ 581
Егер  кесіндісінде кесіндісінде  функциясының таңбалары шектеулі рет ауысса, онда функциясының таңбалары шектеулі рет ауысса, онда  , ,  , ,  , ,  сызықтарымен қоршалған сызықтарымен қоршалған  жазық фигурасының ауданы былай есептелінеді: Ж: жазық фигурасының ауданы былай есептелінеді: Ж: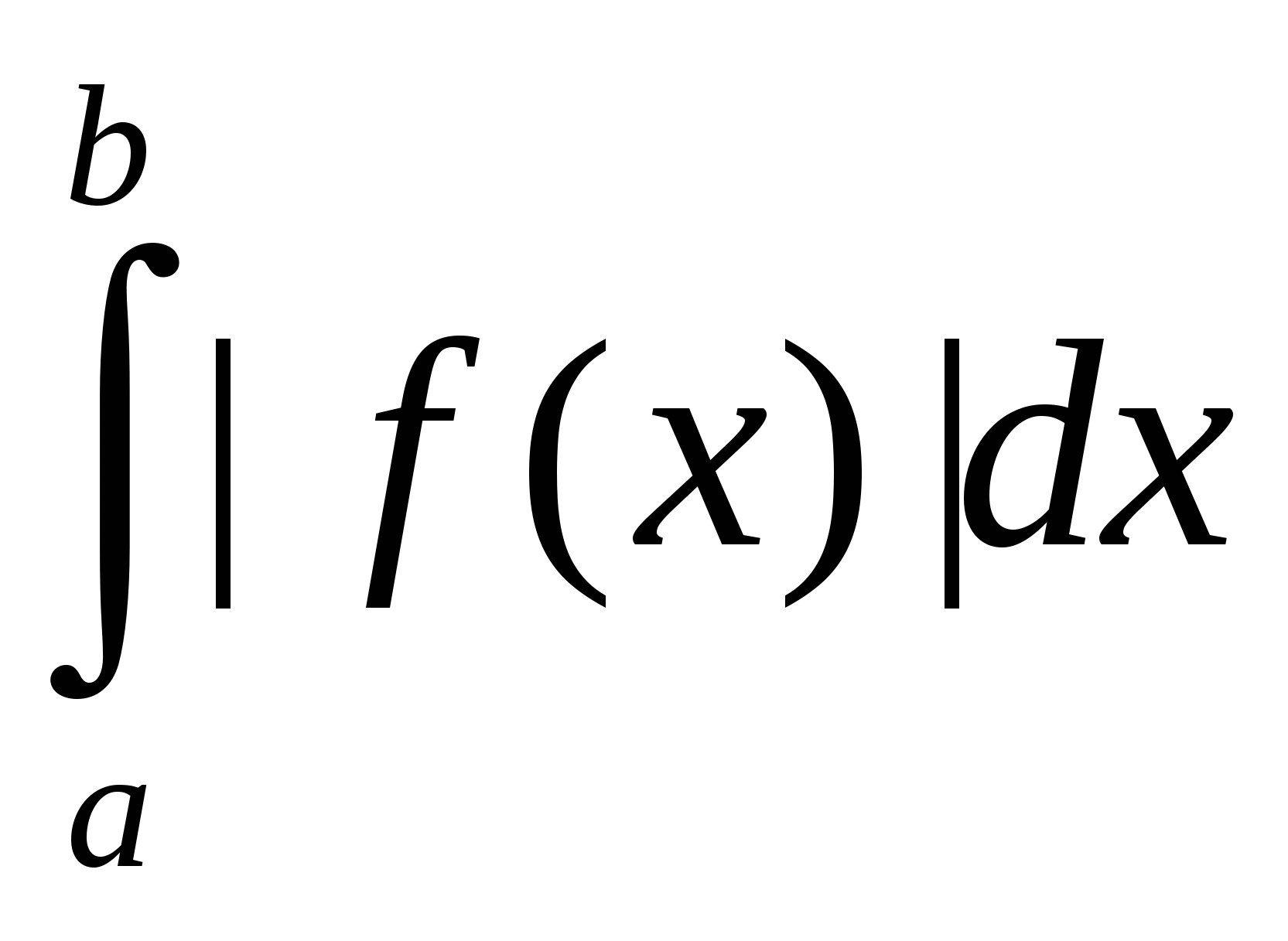
$$$ 582
 , ,  , ,  сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді: Ж: сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді: Ж: 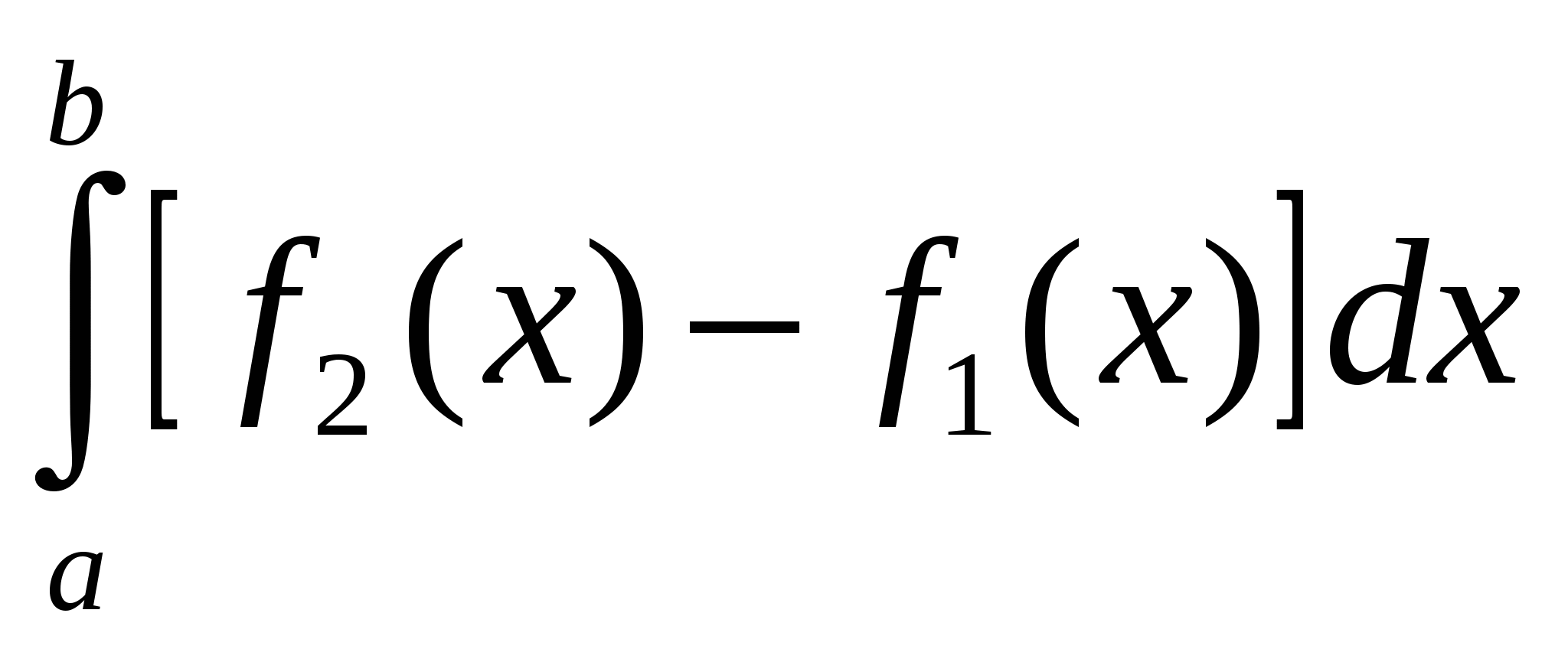
$$$ 583
 сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:1\2 Ж: сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді:1\2 Ж: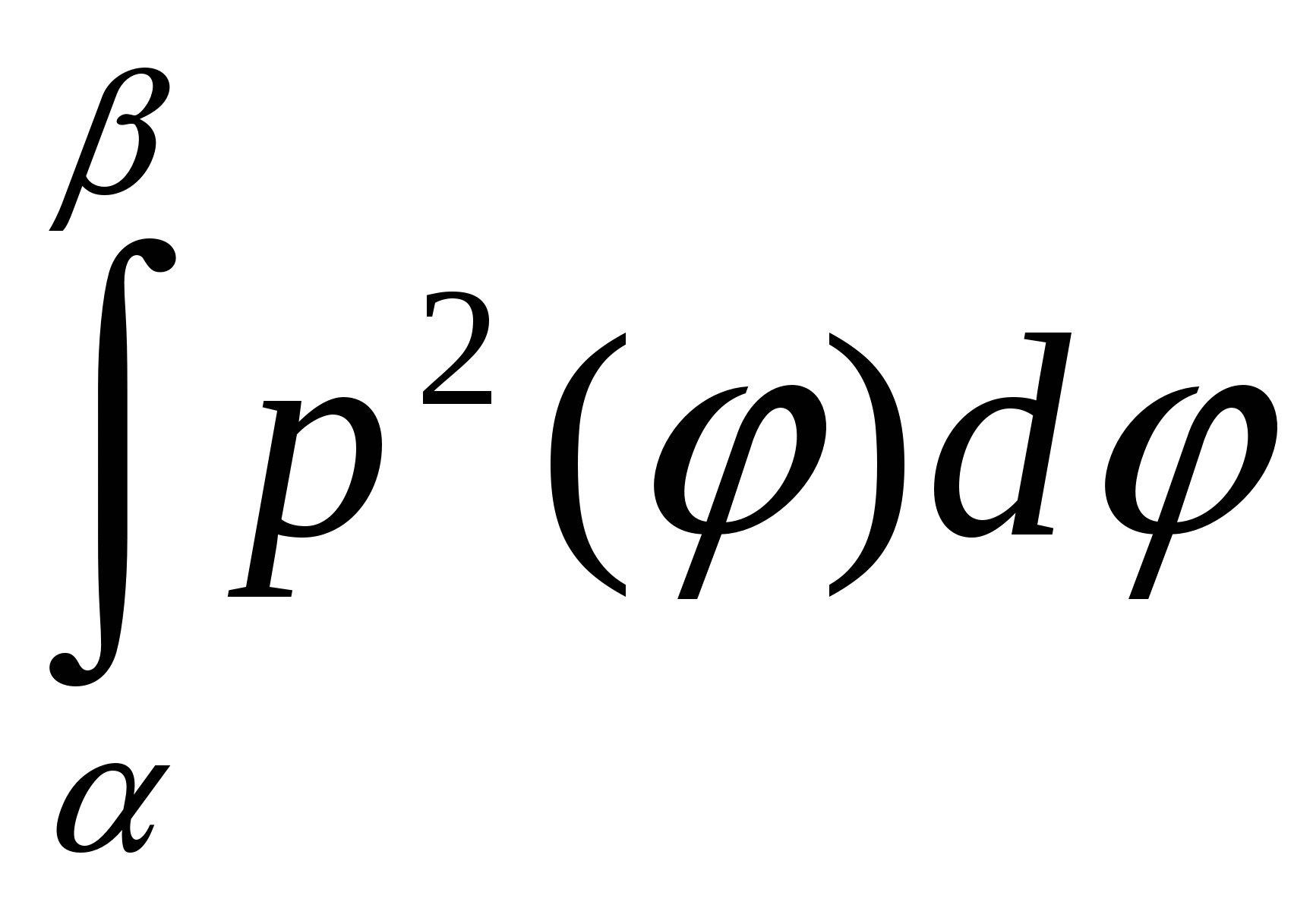
$$$ 584Параметрлік теңдеумен берілген  сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді: Ж: сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді: Ж: 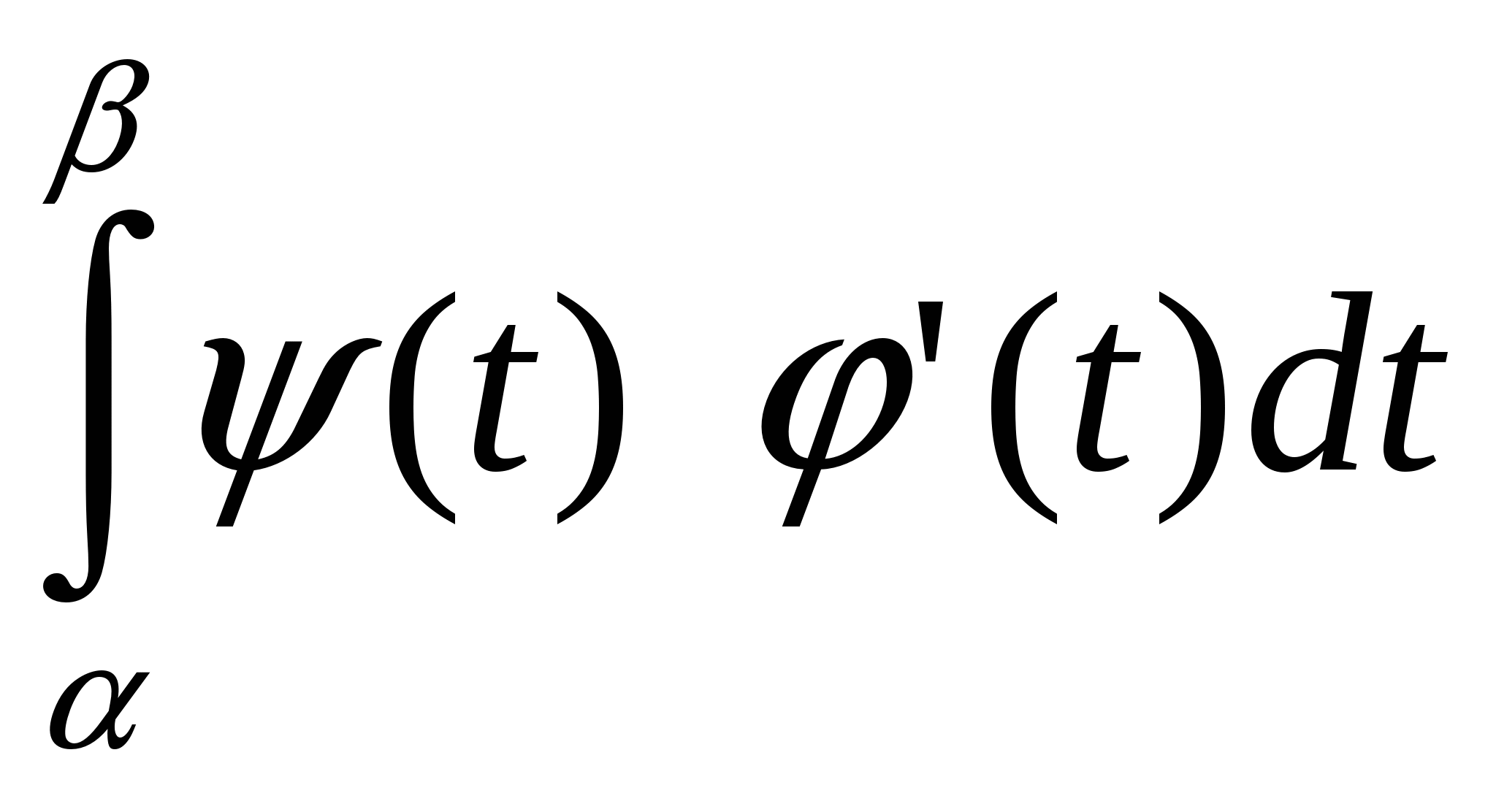
$$$ 585 қисығын қисығын  ( ( ) өсімен айналдырғаннан пайда болған дененіің көлемі былай есептелінеді Ж: ) өсімен айналдырғаннан пайда болған дененіің көлемі былай есептелінеді Ж: 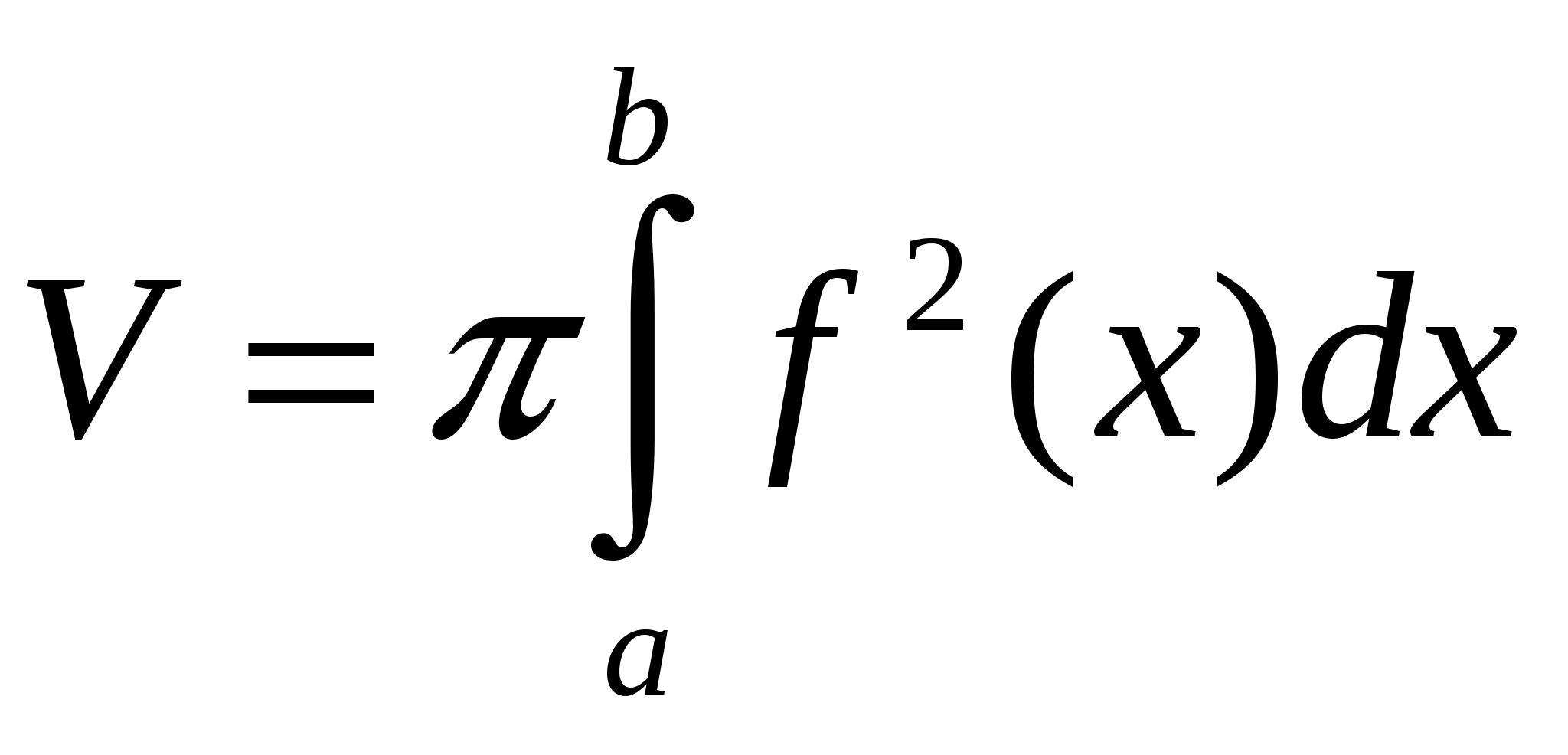
$$$ 586 Ж: Ж: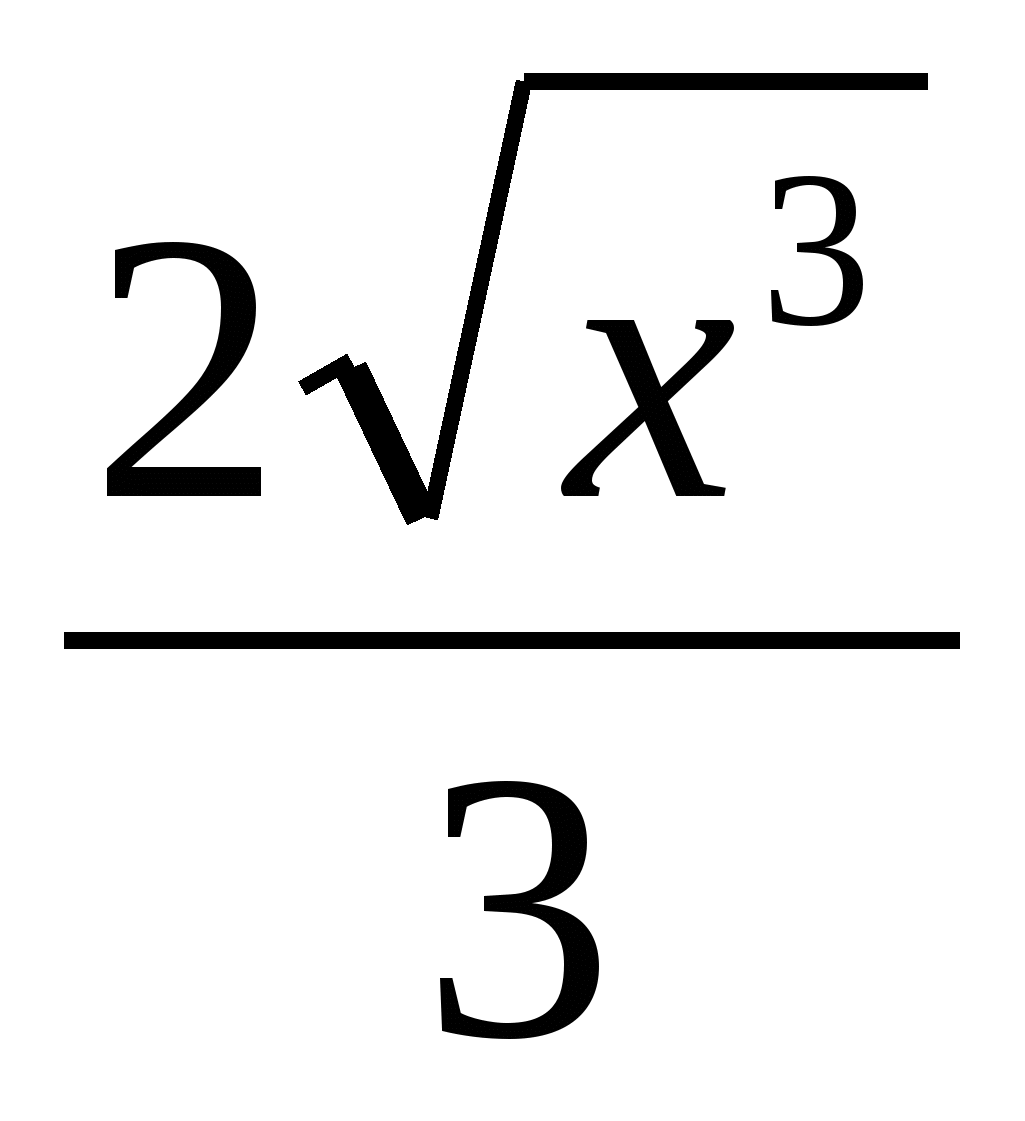
$$$ 587 Ж: Ж: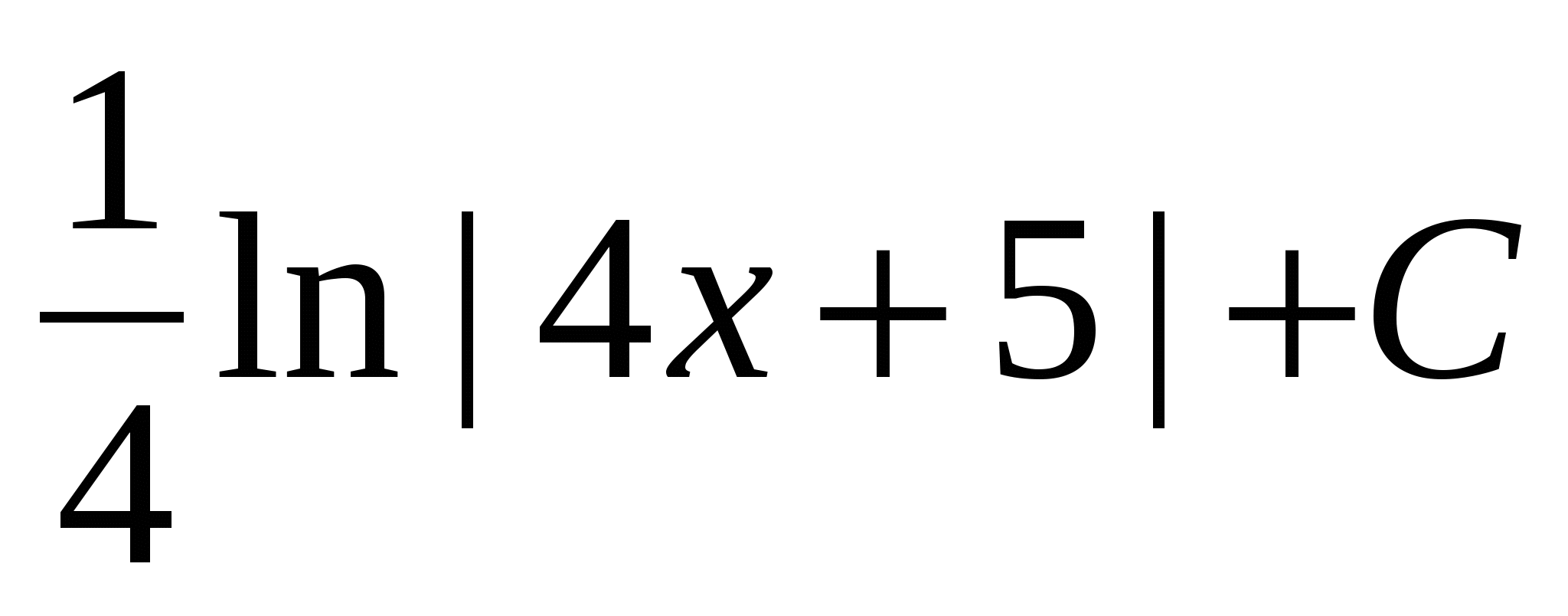
$$$ 588 Ж: - Ж: - 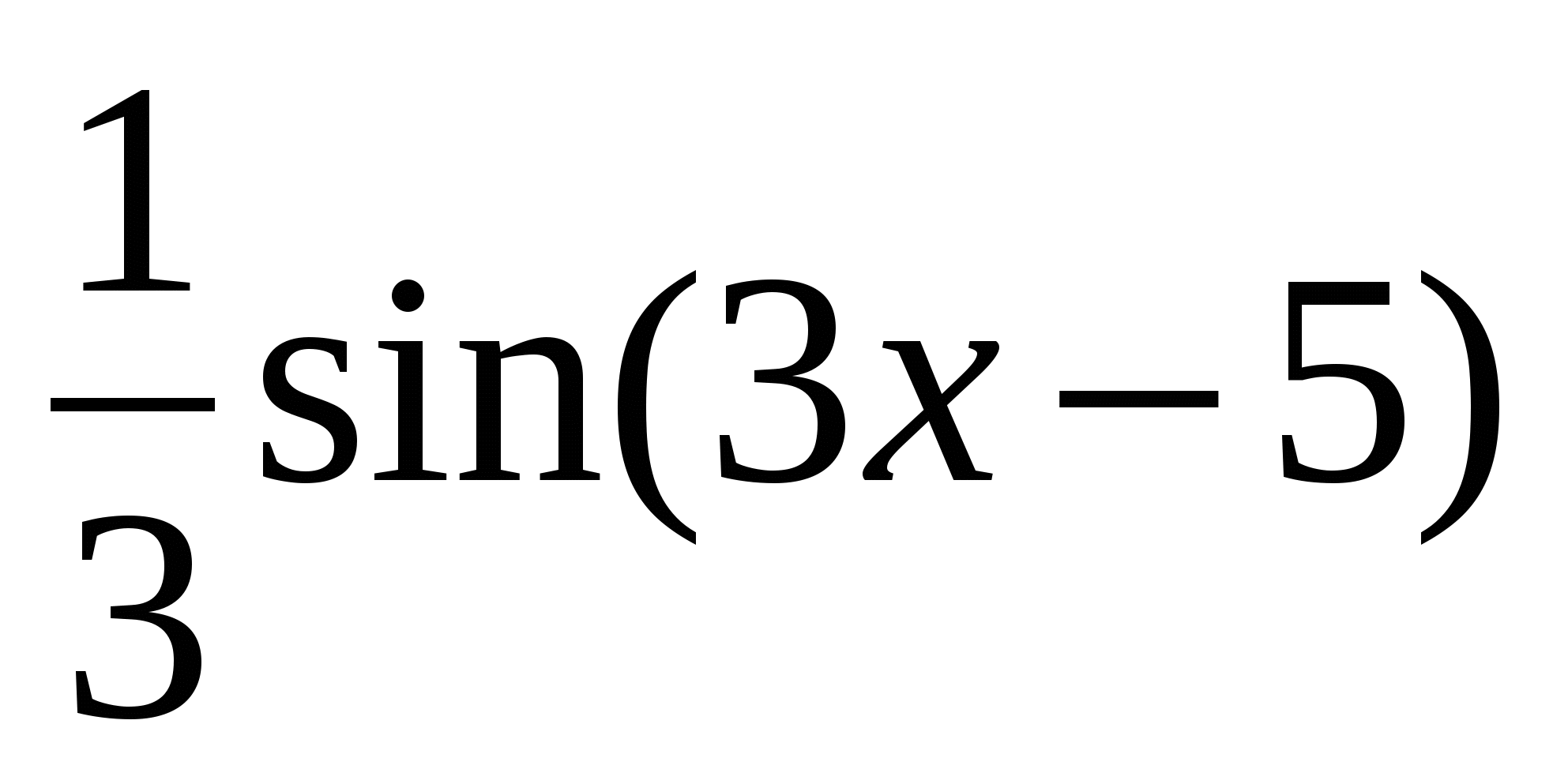
$$$ 589 Ж: cos(5-x) Ж: cos(5-x)
$$$ 590 Ж: Ж: 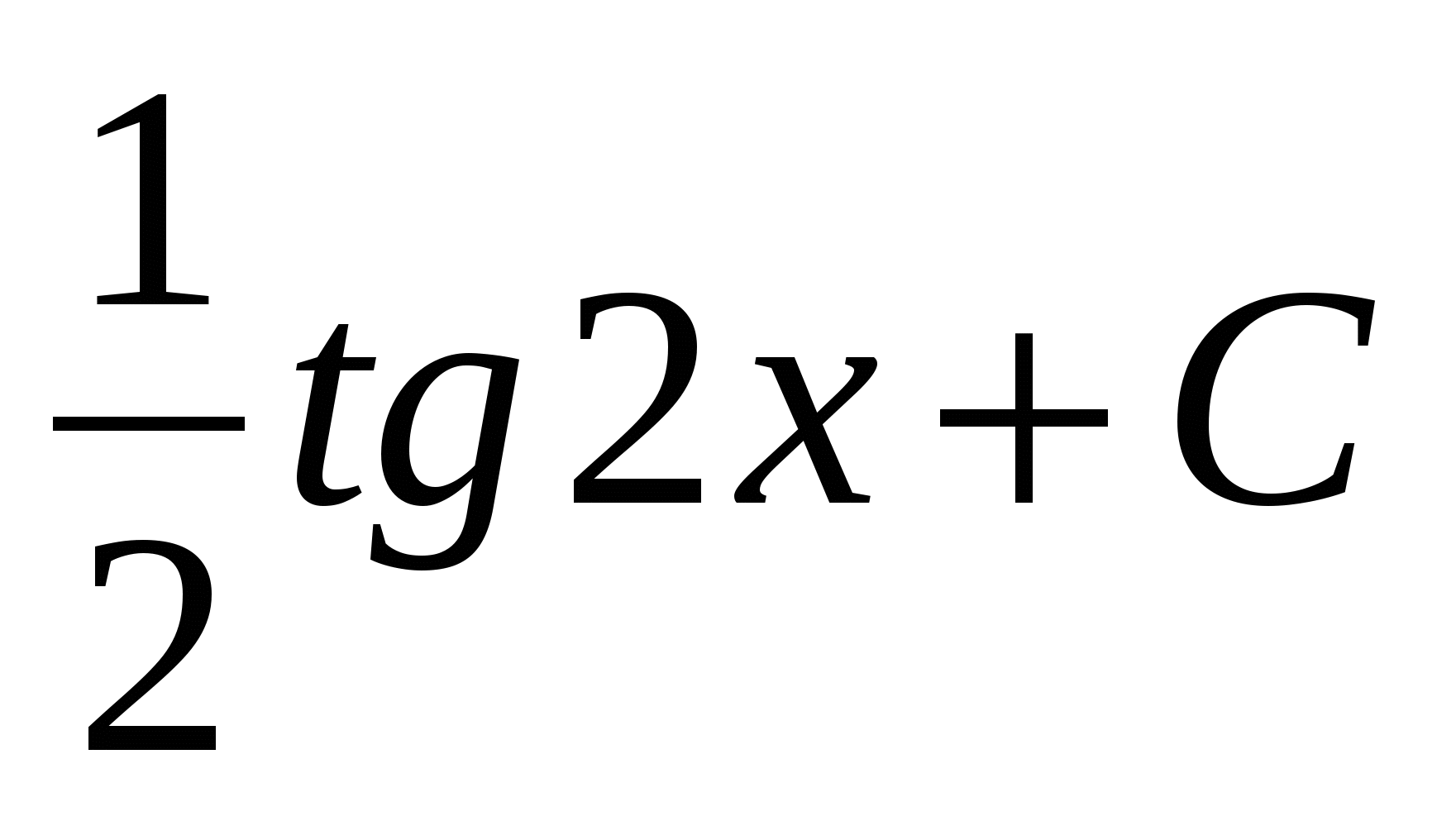
$$$ 591 Ж: Ж: 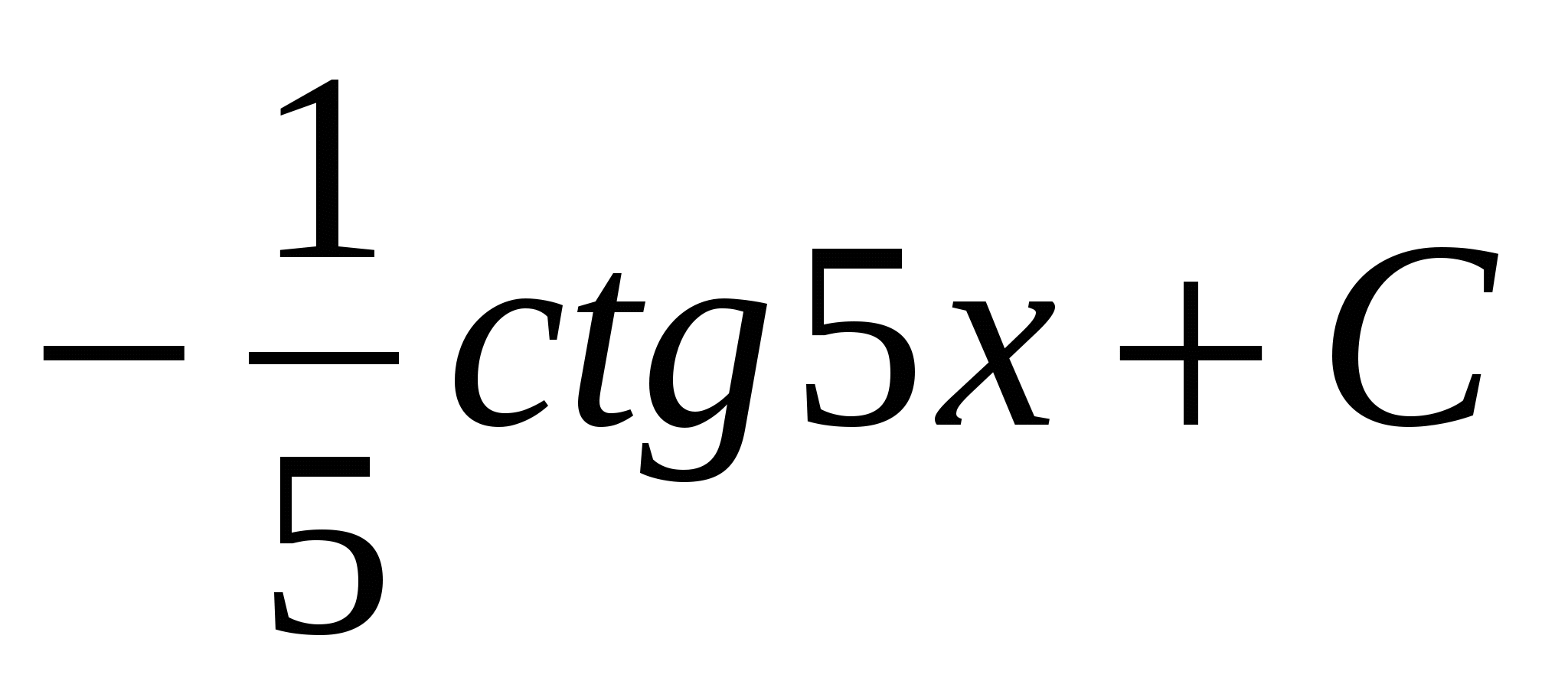
$$$ 592 Ж: Ж: 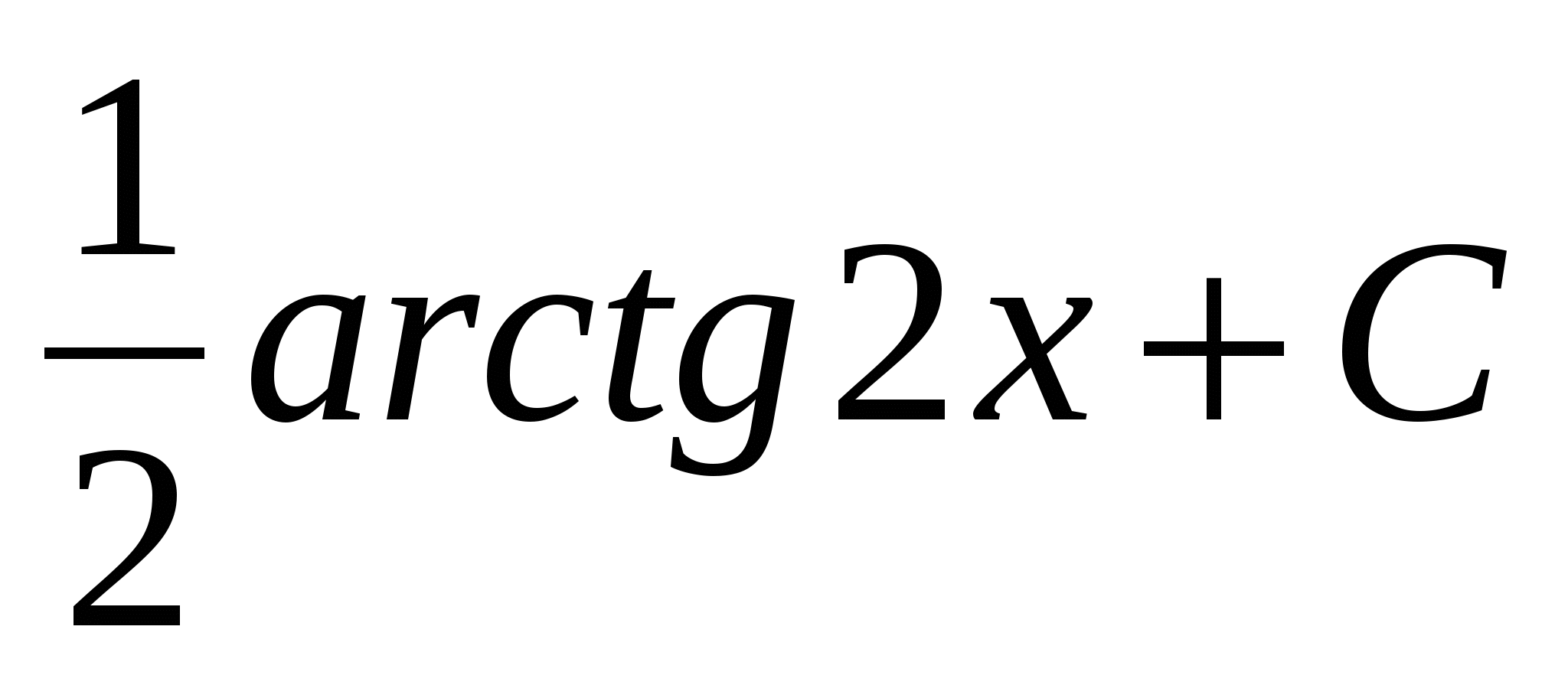
$$$ 593 Ж: Ж: 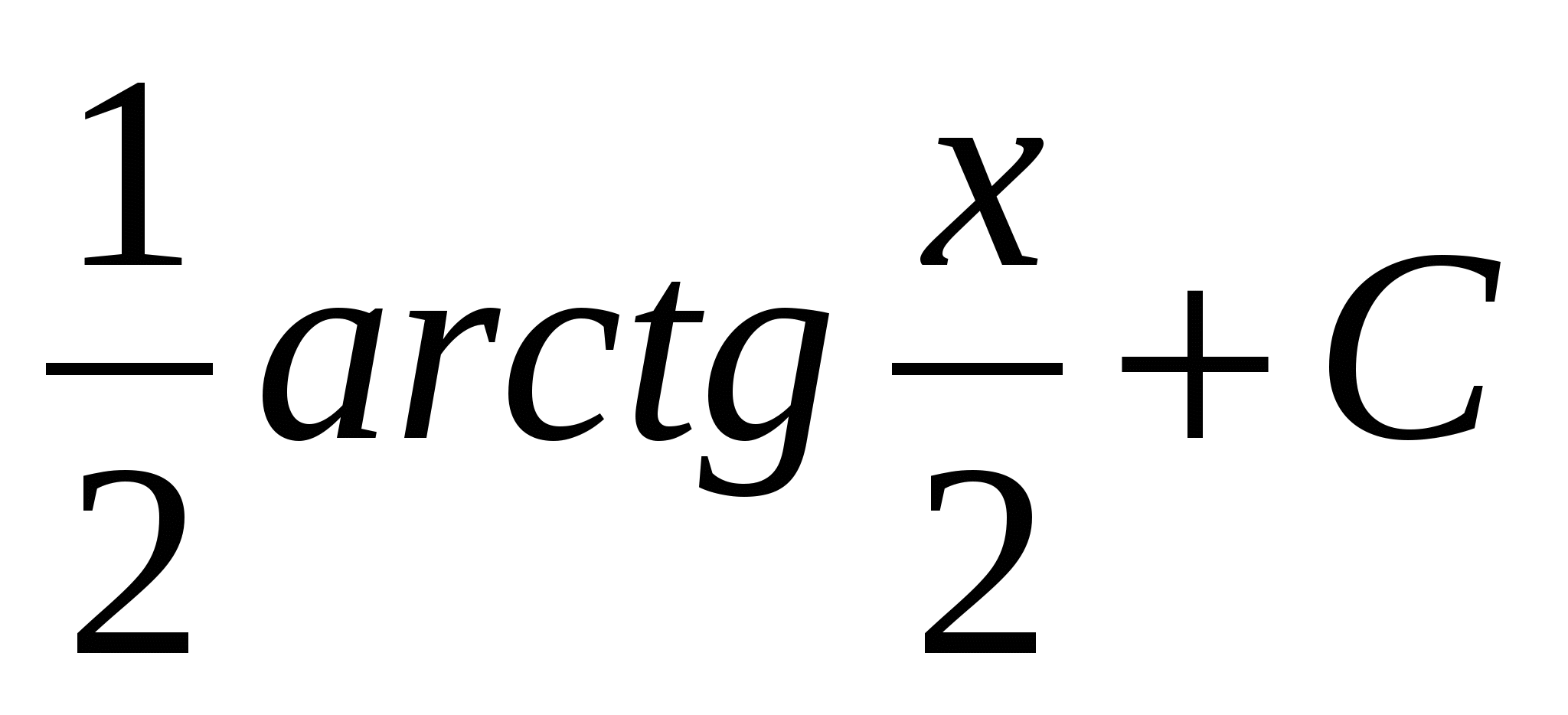
$$$ 594 Ж:arctgx+C Ж:arctgx+C
$$$ 595 Ж: Ж: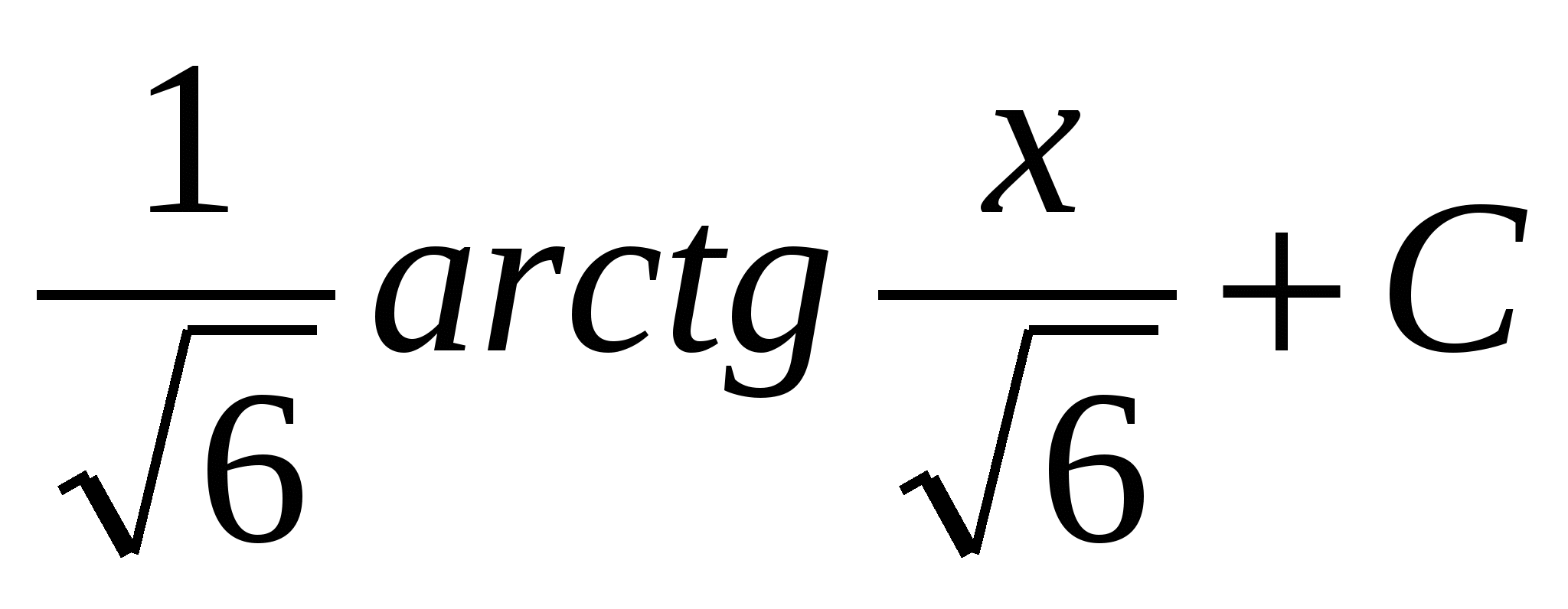
$$$ 596 Ж: Ж: 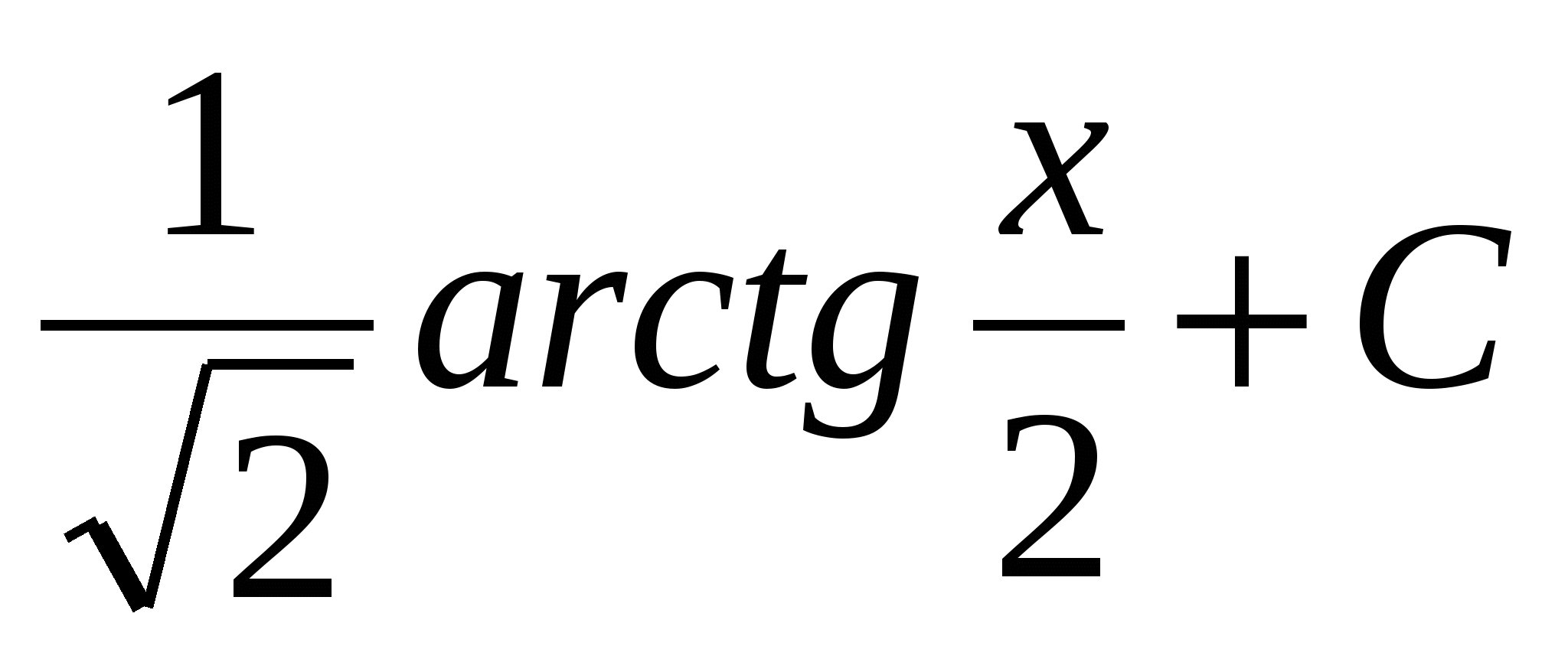
$$$ 597 Ж: arcsinx+C Ж: arcsinx+C
$$$ 598 Ж: Ж: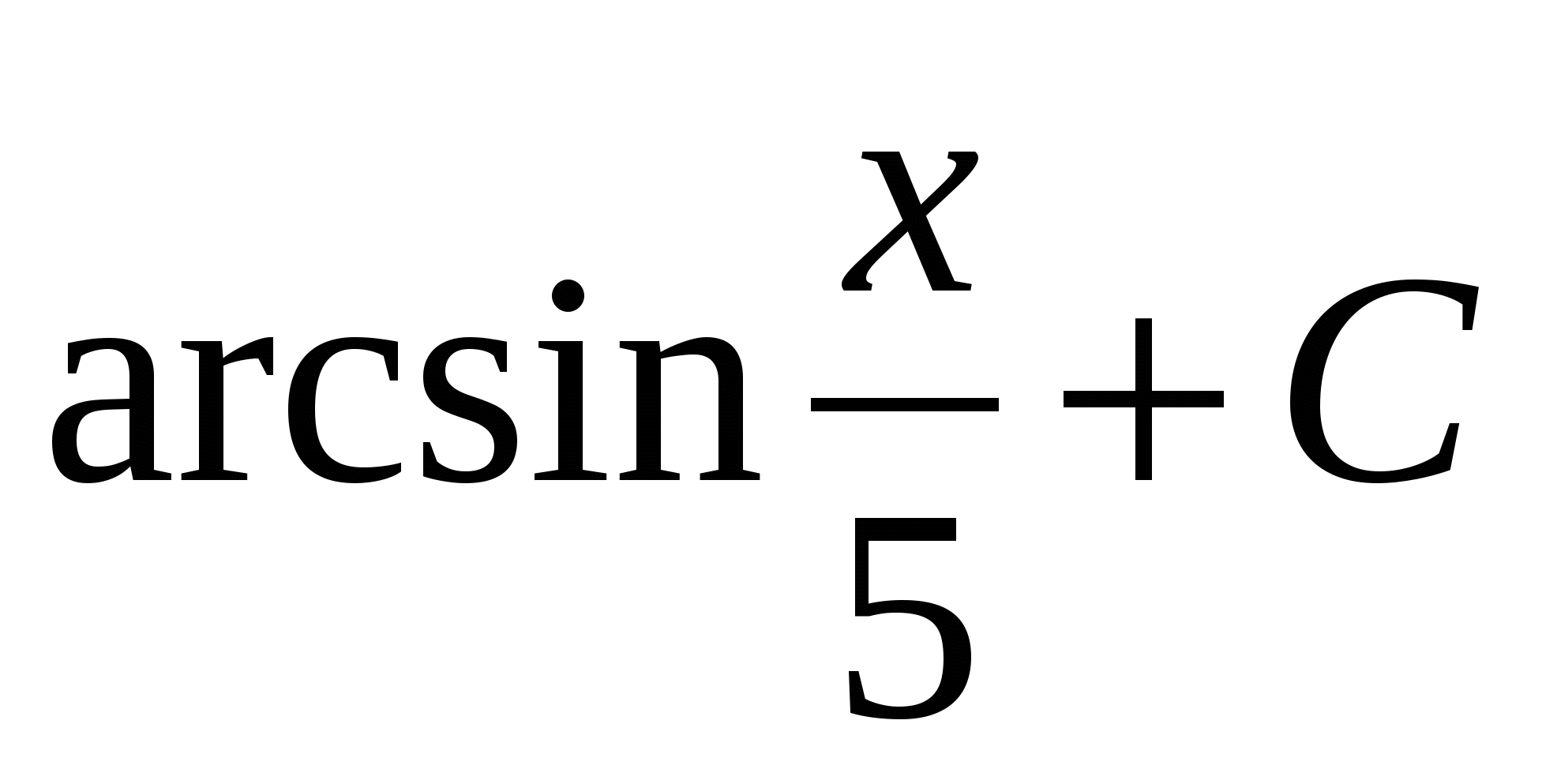
$$$ 599 Ж: Ж: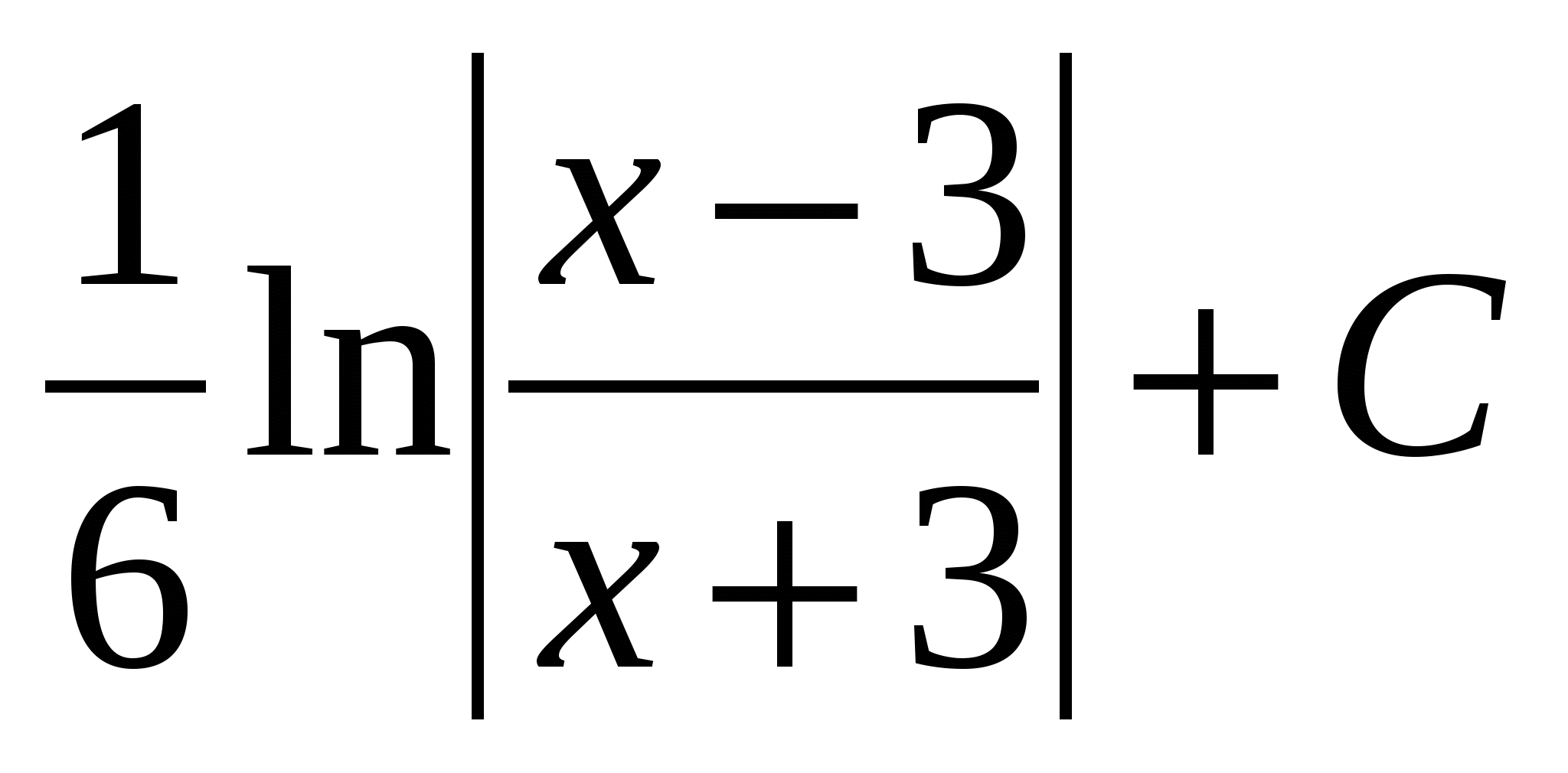
$$$ 600 |
|
|
 Скачать 0.6 Mb.
Скачать 0.6 Mb. туындысының формуласын көрсетіңіз:
туындысының формуласын көрсетіңіз:  Ж:
Ж:  Ж:
Ж:  Ж:2
Ж:2 Ж:0
Ж:0 Ж:
Ж: 