Статья_январь_2008. К оценке одного параметра функциональнонормального распределения
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
Исакова А.Я. К оценке одного параметра функционально-нормального распределения суточных сумм жидких осадков Как известно, ливневые осадки характеризуются большой временной и пространственной изменчивостью. По этой причине, к примеру, Р.К.Линслей с соавторами [3] отмечают, что одним из важных вопросов гидрометеорологии является «перенос ливней», т.е. использование характеристик ливня по данному пункту на другие пункты, или территории. Также верно отмечает А.Ф.Шахидов, что в практике гидрологических расчетов «…наибольшую сложность представляют расчеты максимального стока ливневых вод» и «… причиной разрушений…(сооружений) является превышение максимальных расходов дождевых вод над расчетными». И в дополнение к этому «…применяемые в настоящее время для определения максимального расхода ливневых вод СНиП 2.01.14-83…не учитывают региональные факторы формирования максимального стока» [4]. С учетом последнего замечания для условий Средней Азии разработаны методики расчетов максимумов дождевых паводков Ю.Б.Виноградовым, В.М.Денисовым и А.Ф.Шахидовым [1, 2, 4]. В качестве основных метеорологических параметров используются дождевые осадки редкой повторяемости. Статистической оценкой суточных сумм жидких осадков наиболее полно занимался Ю.Б.Виноградов. Им же даны для 638 осадкомерных пунктов Средней Азии и Южного Казахстана значения среднего числа дождей в году, слоем более 1,0 мм и суточные суммы жидких осадков различной обеспеченности. Имеет смысл напомнить, что в качестве нормализующей функции Ю.Б.Виноградов использовал выражение: где Н – суточная сумма жидких осадков слоем более 1,0 мм, а nH – показатель степени, изменяющийся в довольно узких пределах и для большинства метеопунктов равный 0,30. В дополнение к статистической оценке дождей Виноградовым были получены районные зависимости Hp%=f(Z), где р% - обеспеченности суточного слоя дождя (10 и 0,1% для «усеченной» выборки и 1% для всей совокупности дождей), Z – высота (км). Квантили дождя другой обеспеченности предлагается определять по кривой обеспеченности линейного вида, построенной с использованием упомянутых квантилей распределения. Параметр nH, по мнению Ю.Б.Виноградова, характеризует асимметричность распределения суточных осадков и для его расчета предлагает использовать эмпирическую кривую распределения Н. С учетом «функционального» масштаба распределение суточных осадков, как уже сказано, представляется прямой линией и, выбрав три равноотстоящих значения Н, можно рассчитать параметр nH 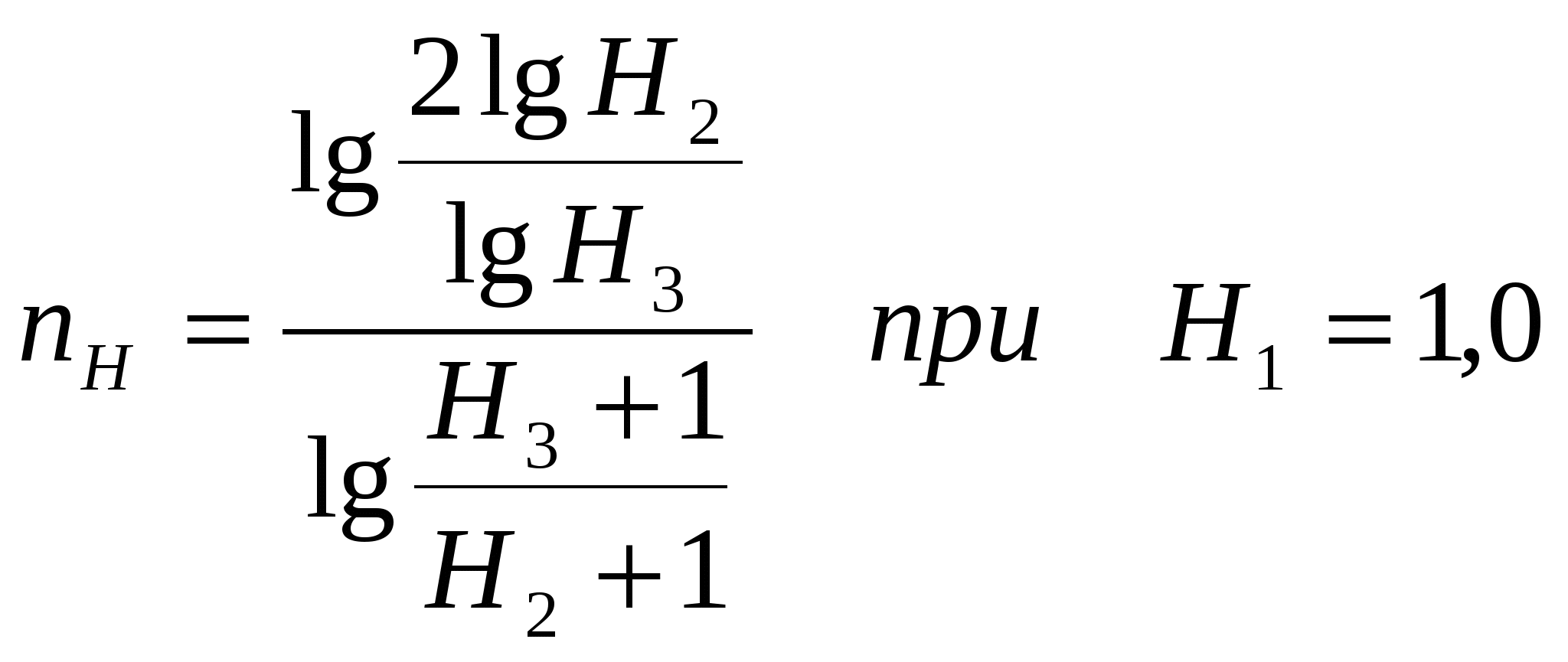 . (2) . (2)Нужно отметить, что, во-первых, не всегда удается аппроксимировать распределение обеспеченностей линейной связью и, во-вторых, при статистическом моделировании дождей необходима оценка параметра nH. В данной работе использованы значения nH для 233 метеопунктов Узбекистана и сопредельных территорий. В (табл. 1) приведены основные статистические характеристики распределения nH для всего Узбекистана и для выделенных районов. Таблица 1 Значения nH для метеопунктов Узбекистана
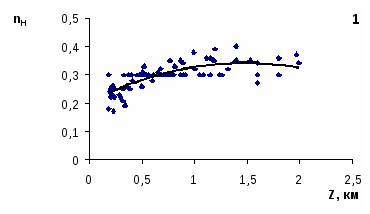
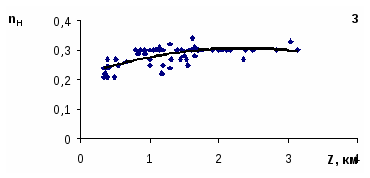
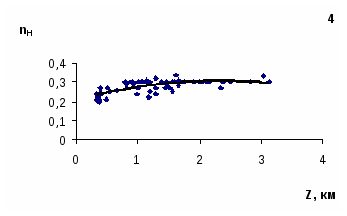
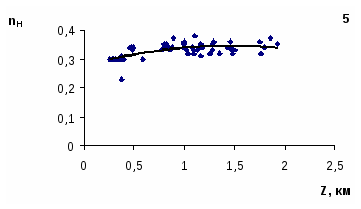
В дальнейшем, сохраняя схему районирования Виноградова, для пяти крупных районов Узбекистана были получены зависимости показателя степени nH от высоты местности (рис. 1). Как видно из приведенных зависимостей связи nH с высотой в целом повторяют аналогичные связи для всех характеристик жидких осадков – от предгорий до зоны гор в 1,5-2 км наблюдается рост nH. Максимум значений nH в диапазоне 1,5-2,0 км, затем величины этого параметра с ростом высоты местности уменьшаются, что связано с высотным изменением температур воздуха и увеличением доли твердых осадков на больших высотах. Зависимости nH=f(Z) для всех районов имеют вид: Значения параметров уравнений и коэффициенты тесноты связи для выбранных районов и для всей Республики приведены в (табл. 2). Таблица 2 Параметры связей nH=f(Z)
Как видно из (табл. 2) связи характеризуются относительно невысокими значения коэффициентов связи, что лишний раз говорит о большой пестроте распределения дождей. 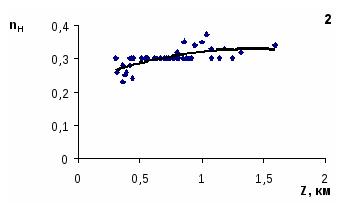
Отметим, что примерно для 45% метеопунктов Узбекистана значение показателя степени nH равно 0,30, однако, использование вычисленных по уравнению (3) значений этого показателя для малых рек, расположенных в различных географических и высотных зонах позволит более корректно выполнять расчеты суточных осадков различной обеспеченности и, соответственно, максимумов дождевых паводков. Литература
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||