ваы. К виду 2) можно прийти одним из следующих способов
 Скачать 113.62 Kb. Скачать 113.62 Kb.
|
|
А) Линейное уравнение это математическое выражение. Там переменные просто складываются или вычитаются. А в нелинейном уравнении неизвестные могут перемножаться, возводиться в степень, иметь квадратный корень из неизвестной или присутствует деление на переменную. Б) Для решения второй подзадачи существуют численные методы, из которых рассмотрим методы итераций, Ньютона и половинного деления. В) Если функция f(x) непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков, то на этом отрезке существует по крайней мере один корень уравнения. Г) Уравнение приводится к виду x=(x), что всегда можно сделать многими способами. Например, задано уравнение 5x-lnx=0. К виду (2.2) можно прийти одним из следующих способов: 1) x=5x-lnx+x=6x-lnx; 2) -x=5x-lnx-x, или x=lnx-4x; 3) x= 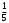 lnx. lnx.Геометрическая интерпретация метода итераций приведена на рис. 2.3. 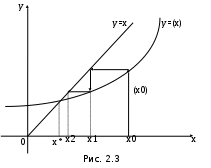  Возьмем на отрезке [,] произвольную точку x0 -начальное приближение и примем в качестве следующего приближения Возьмем на отрезке [,] произвольную точку x0 -начальное приближение и примем в качестве следующего приближенияx1= (x0). Затем аналогичным образом получим: x2= (x1), . . . . . . . . . xn= (xn-1). Процесс итераций следует продолжать до тех пор, пока не будет выполнено условие 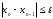 , где - заданная погрешность определения корня x* . , где - заданная погрешность определения корня x* .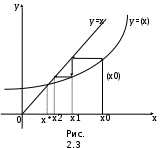 Метод итераций сходится, т.е. дает числовую последовательность x0, x1, x2, и т.д., сходящуюся к x*, если на отрезке [, ] выполняется условие 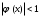 и расходится, если и расходится, если 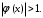 Д) Пусть дано уравнение (2.1), где функция f(x) непрерывна на отрезке [,] и f()f()<0. Для нахождения корня уравнения f(x), принадлежащего отрезку [,], делим отрезок пополам, т.е. выбираем начальное приближение 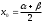 (рис. 2.5). Если f(x0)=0, то x0 является корнем уравнения. Если f(x0) (рис. 2.5). Если f(x0)=0, то x0 является корнем уравнения. Если f(x0) 0, то выбираем тот из отрезков [, x0] или [x0, ], на концах которого функция f(x) имеет противоположные знаки. Полученный отрезок снова делим пополам, проводим то же рассмотрение и т.д. 0, то выбираем тот из отрезков [, x0] или [x0, ], на концах которого функция f(x) имеет противоположные знаки. Полученный отрезок снова делим пополам, проводим то же рассмотрение и т.д. Процесс деления отрезков пополам продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданной точности (-<). Е)Пусть уравнение f(x)=0 имеет один корень на отрезке [, ], функция дифференцируема на этом отрезке, причем 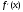 и и 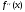 непрерывны и сохраняют постоянные знаки. непрерывны и сохраняют постоянные знаки. 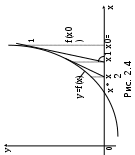 Возьмем некоторую точку x0 отрезка [,] и проведем в точке 1 графика функции касательную к кривой y=f(x) до пересечения с осью абсцисс. Координату x1 точки пересечения можно взять в качестве приближенного значения корня. Проведя касательную через новую точку 2 и находя точку ее пересечения с осью ОХ, получим второе приближение корня x2 и т.д. Возьмем некоторую точку x0 отрезка [,] и проведем в точке 1 графика функции касательную к кривой y=f(x) до пересечения с осью абсцисс. Координату x1 точки пересечения можно взять в качестве приближенного значения корня. Проведя касательную через новую точку 2 и находя точку ее пересечения с осью ОХ, получим второе приближение корня x2 и т.д. 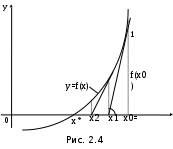 Выведем формулу для последовательных приближений к корню. Уравнение касательной, проходящей через точку 1, имеет вид: 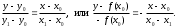 С другой стороны, 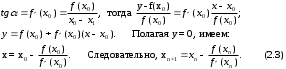 Вычисления по формуле (2.3) продолжаются до тех пор, пока не будет выполняться условие 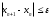 . .Начальное приближение x0 целесообразно выбирать так, чтобы выполнялось условие: 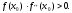 (2.4) (2.4)В противном случае сходимость метода Ньютона не гарантируется. Чаще всего выбирают x0= или x0=, в зависимости от того, для какой из этих точек выполняется условие (2.4). Ж) Метод Ньютона. |
