Лабораторная работа №1 Приближенное вычисление уравнения 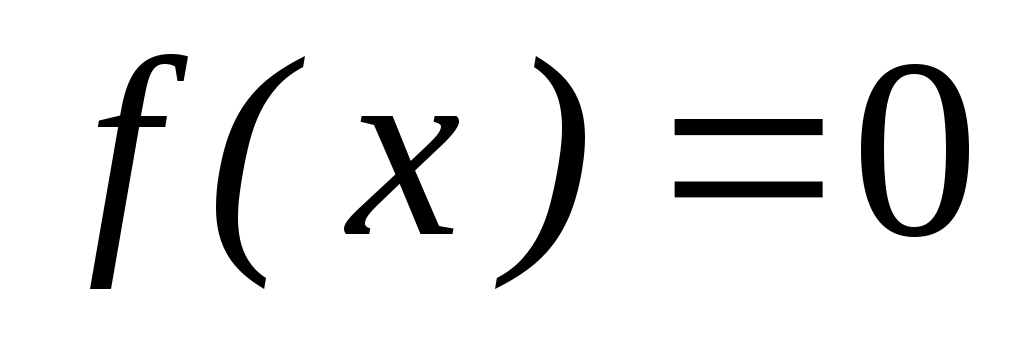 методом деления пополам (методом бисекций) методом деления пополам (методом бисекций)
Пусть задана непрерывная функция 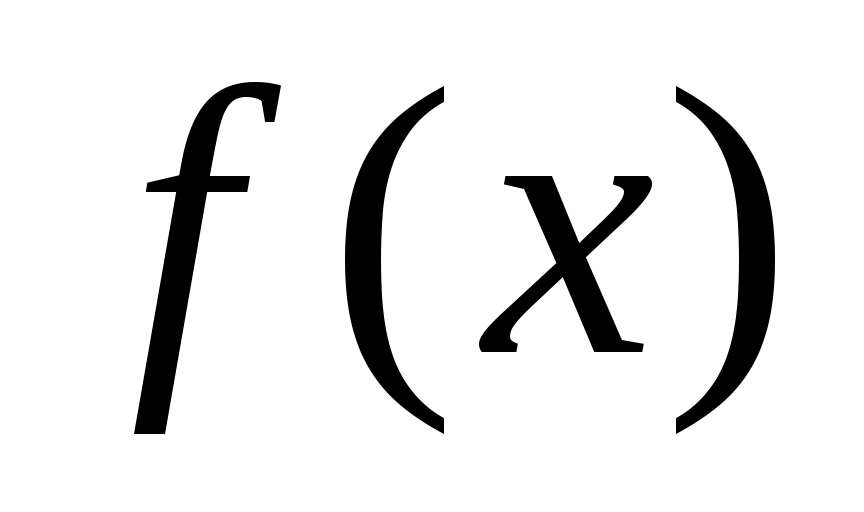 и требуется найти корень уравнения и требуется найти корень уравнения 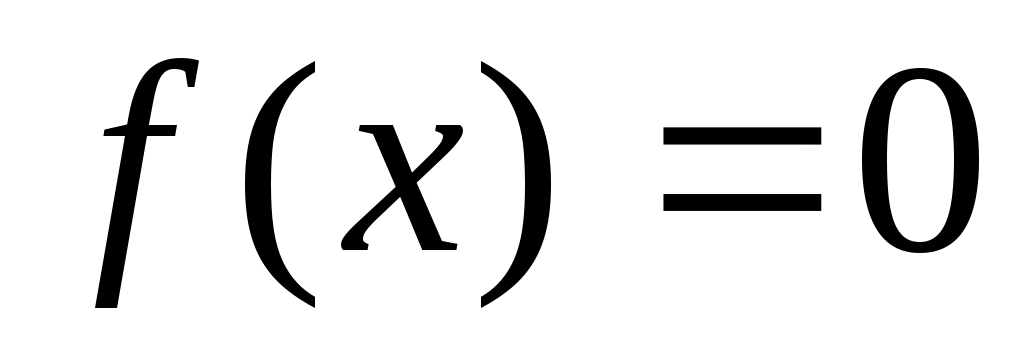 . Предположим, что найден отрезок . Предположим, что найден отрезок 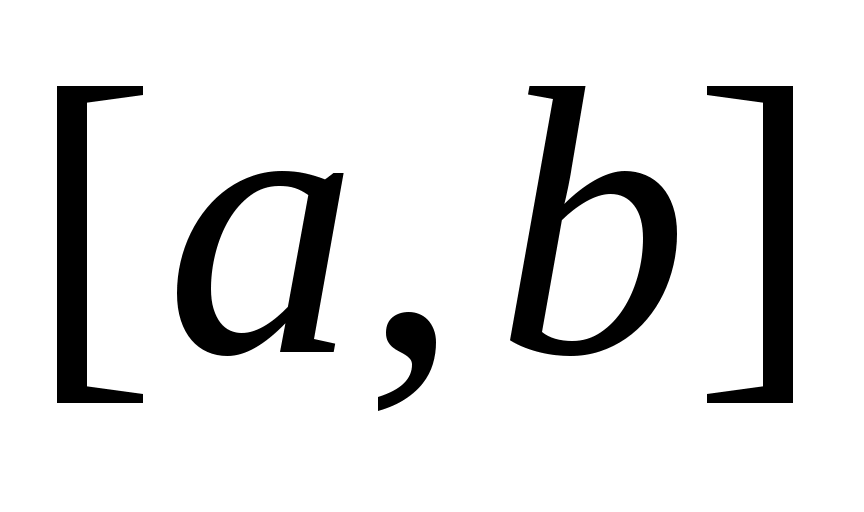 , такой, что , такой, что 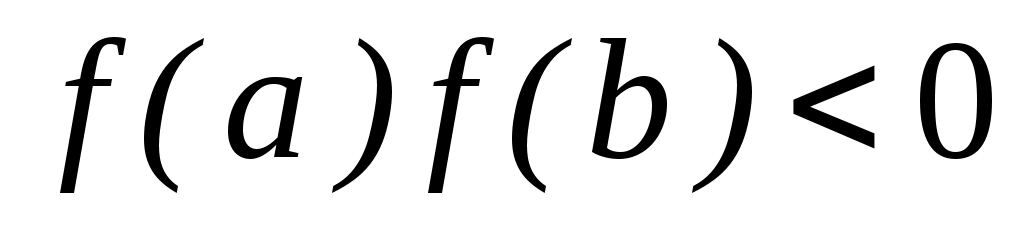 . Тогда согласно теореме Больцано-Коши внутри отрезка . Тогда согласно теореме Больцано-Коши внутри отрезка 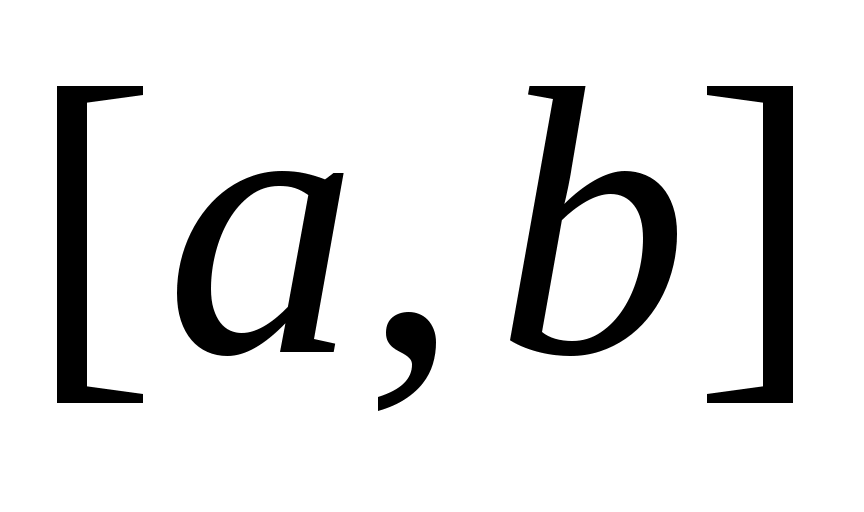 существует точка существует точка 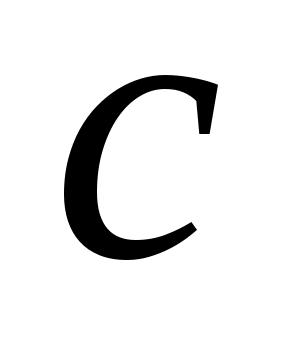 , в которой значение функции равно нулю, т.е. , в которой значение функции равно нулю, т.е. 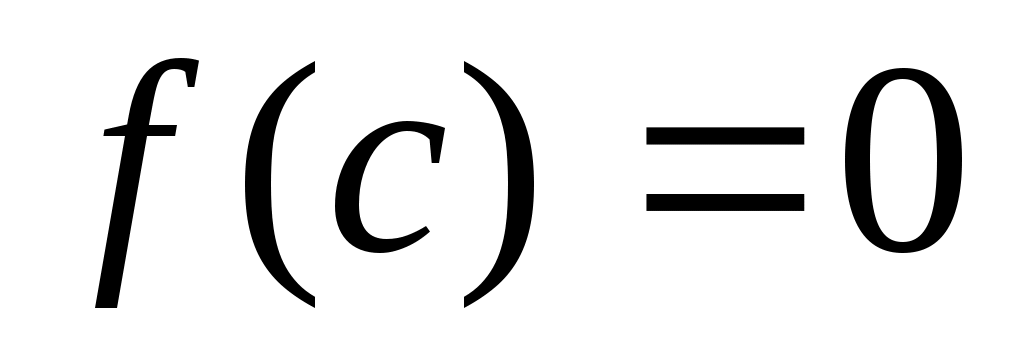 , , 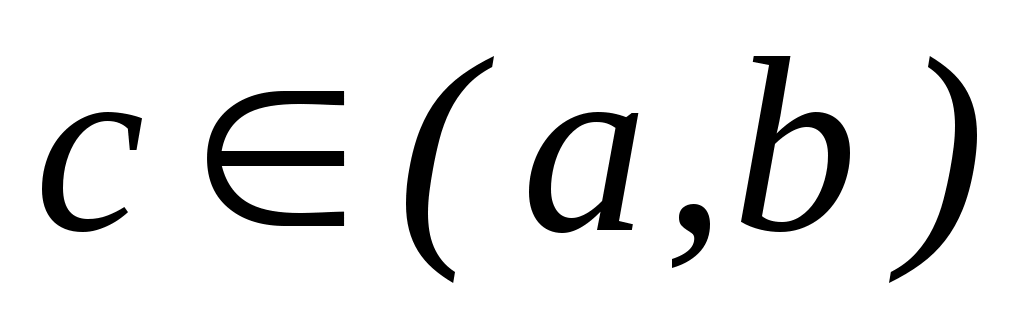 . Итерационный метод бисекций состоит в построении последовательности вложенных отрезков . Итерационный метод бисекций состоит в построении последовательности вложенных отрезков 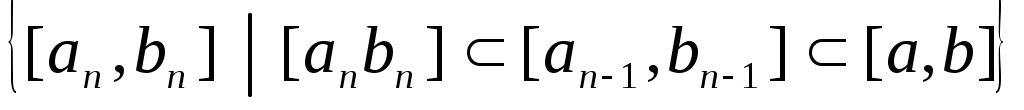 , на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти нуль функции , на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти нуль функции 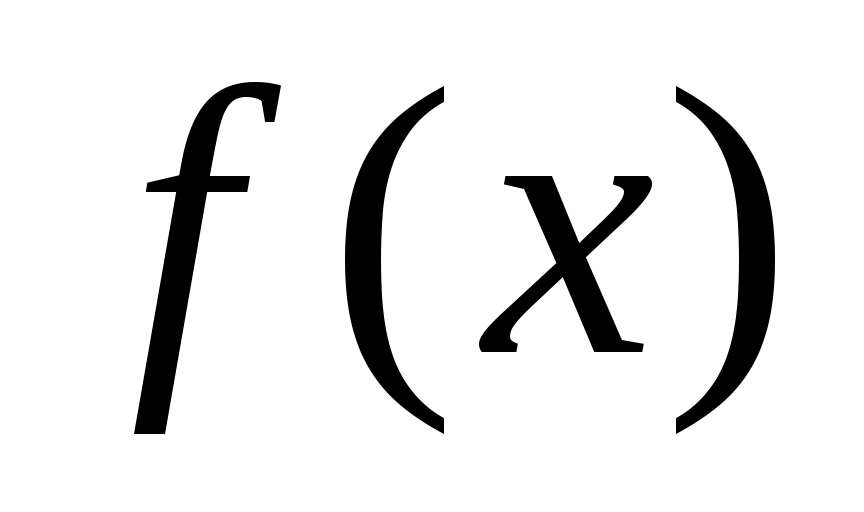 (корень уравнения (корень уравнения 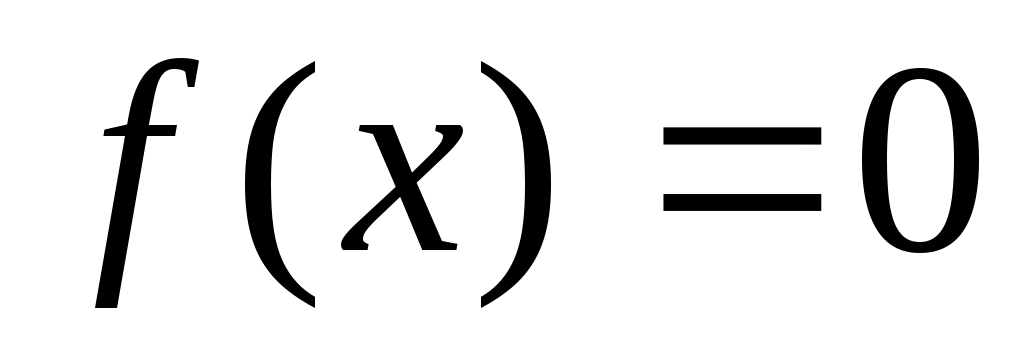 ) с любой заданной точностью. ) с любой заданной точностью.
Опишем один шаг итераций. Пусть на 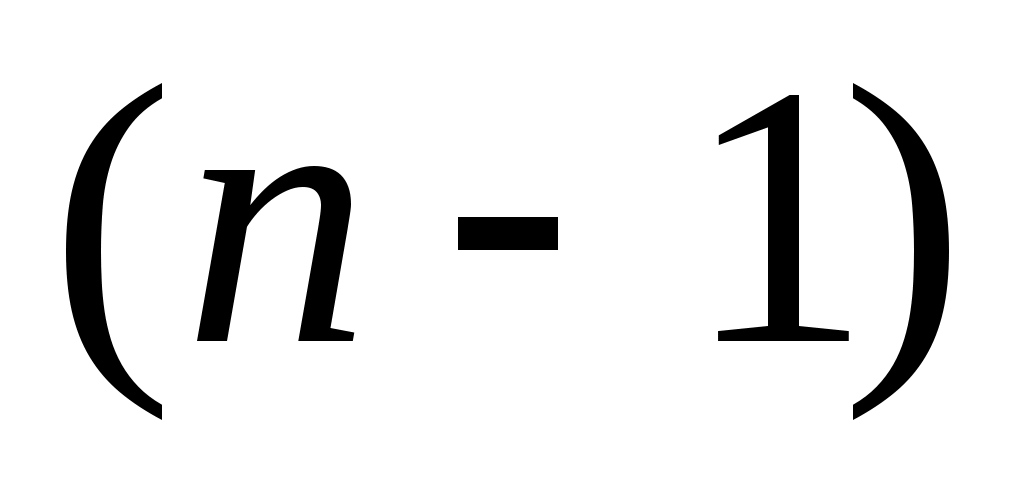 -м шаге найден отрезок -м шаге найден отрезок 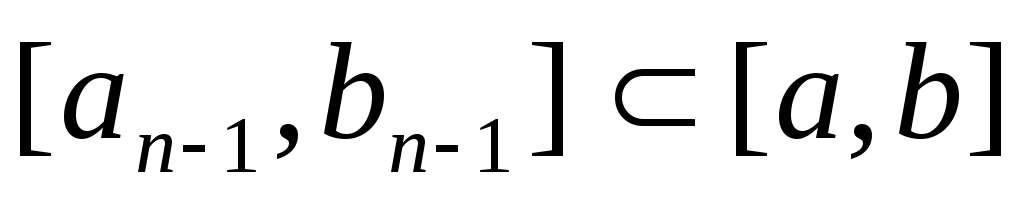 , такой, что , такой, что 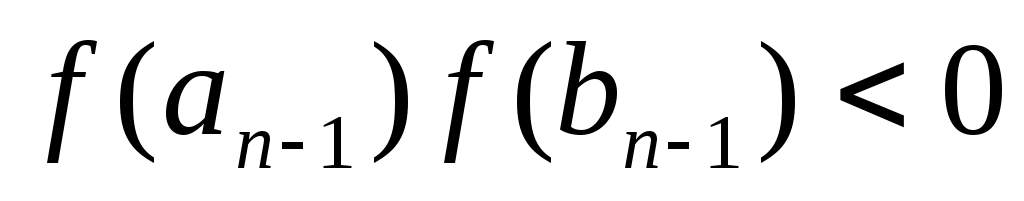 . Делим его пополам точкой . Делим его пополам точкой 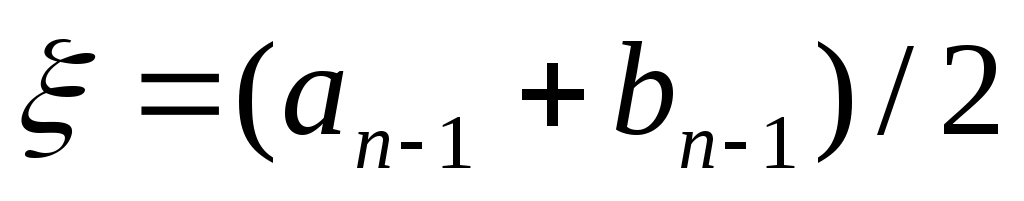 и вычисляем и вычисляем 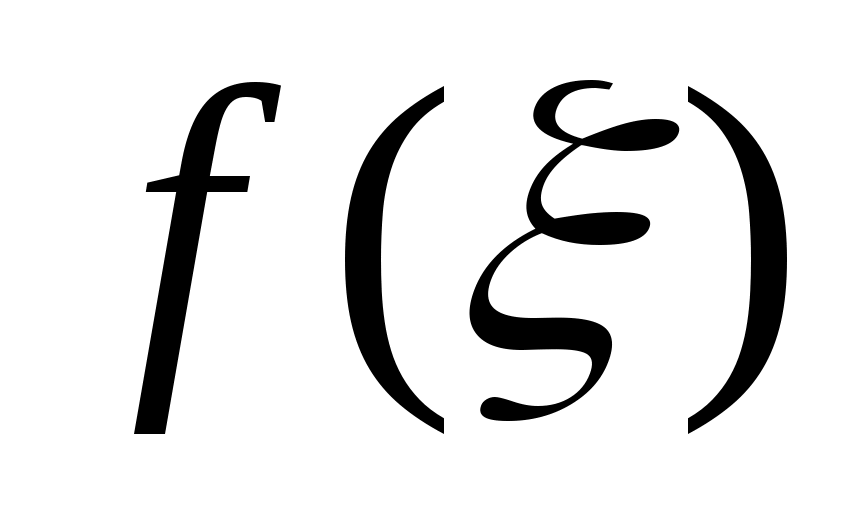 . Если . Если 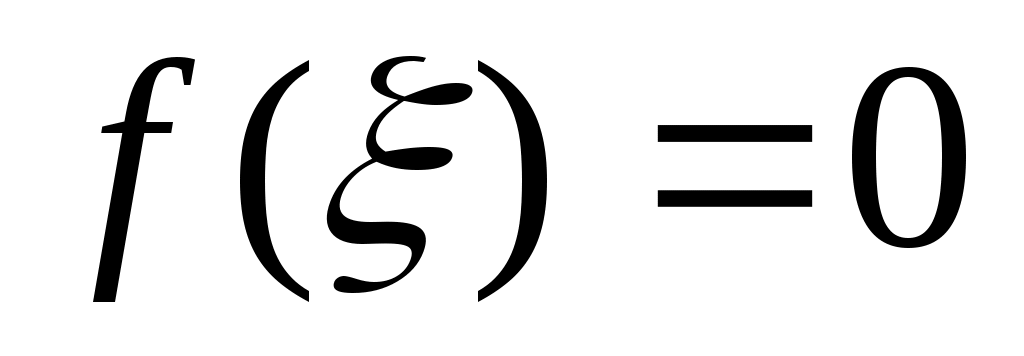 , то , то 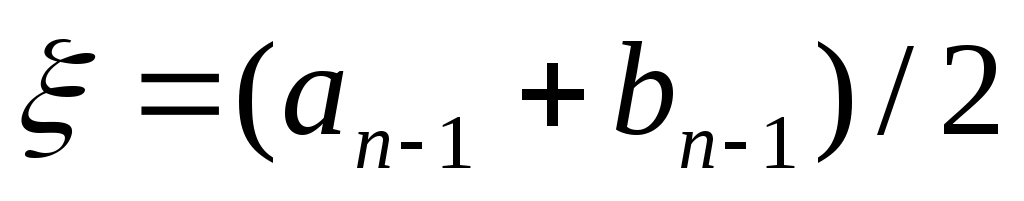 корень уравнения. Если корень уравнения. Если 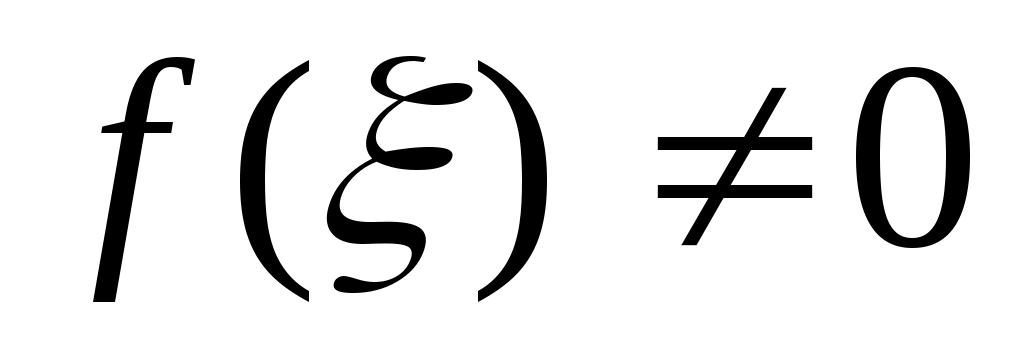 , то из двух половин отрезка выберем ту, на концах которой функция имеет противоположные знаки, так как один из корней лежит на этой половине. Таким образом, , то из двух половин отрезка выберем ту, на концах которой функция имеет противоположные знаки, так как один из корней лежит на этой половине. Таким образом,
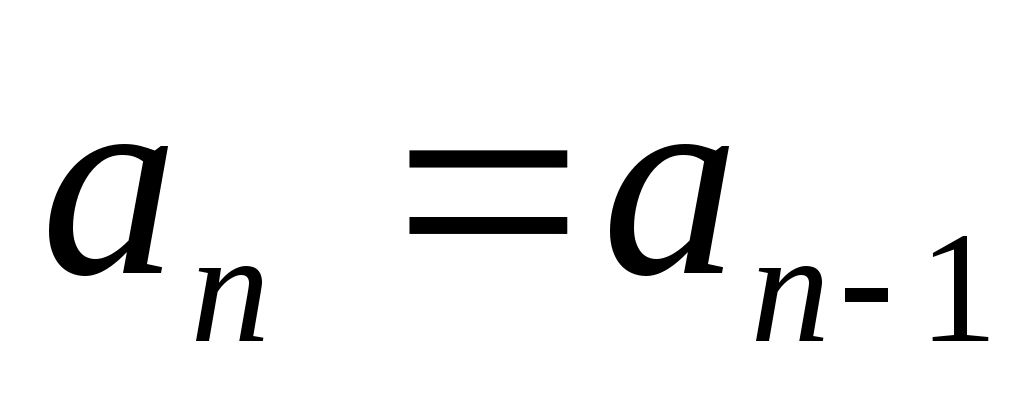 , , 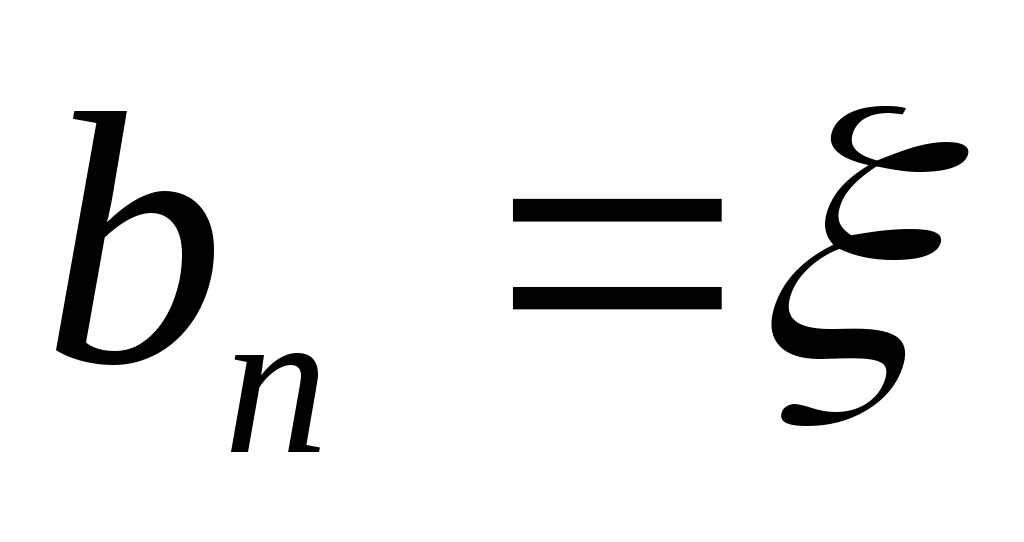 , если , если 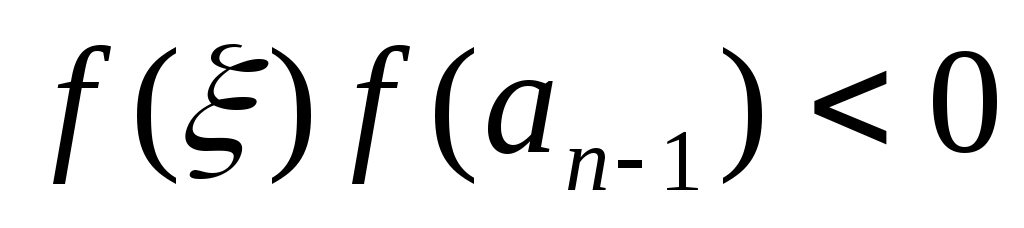 , ,
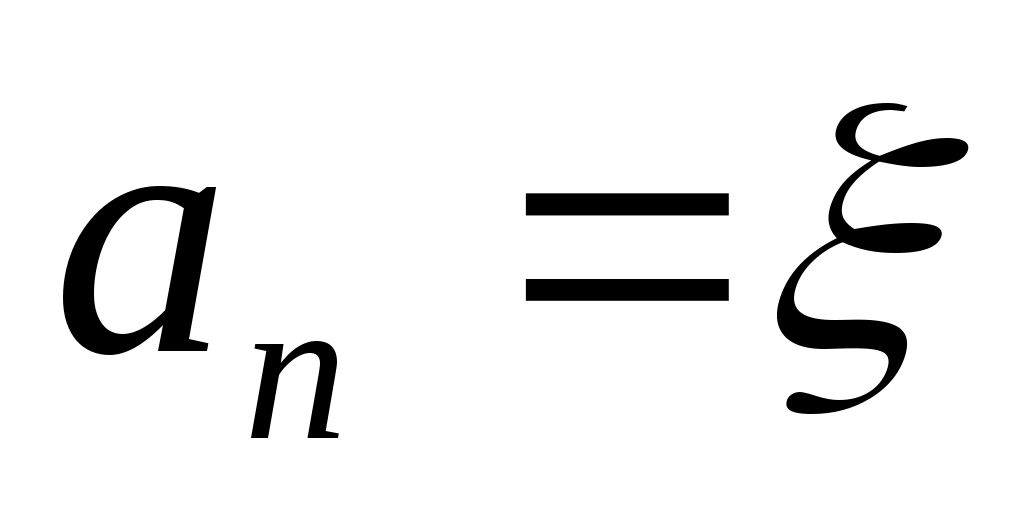 , , 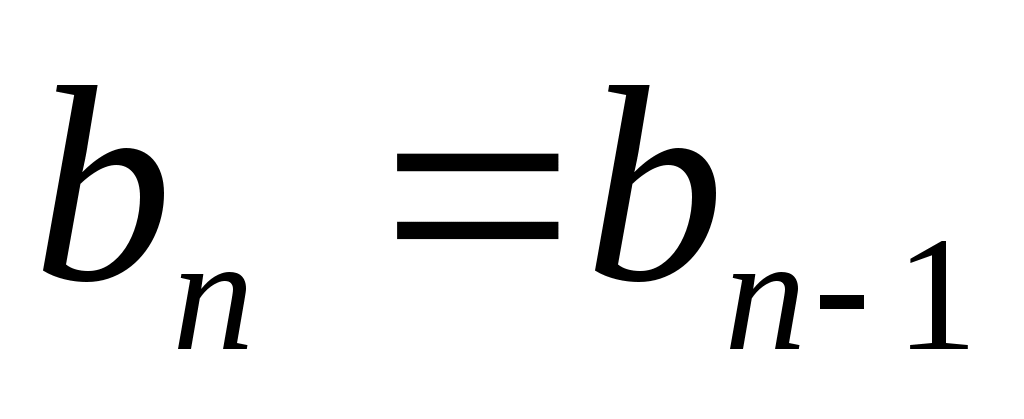 , если , если 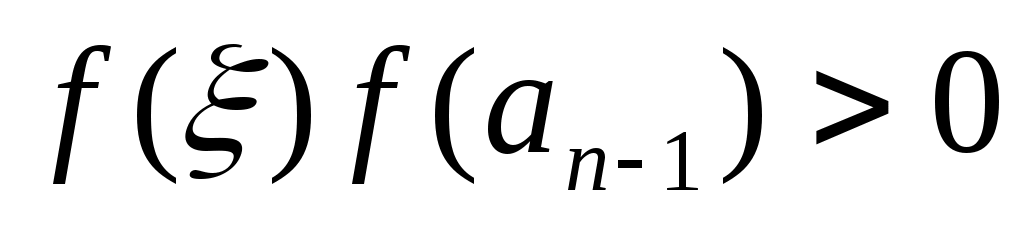 . .
Если требуется найти корень с точностью 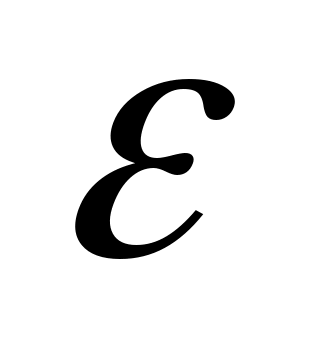 , то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше , то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 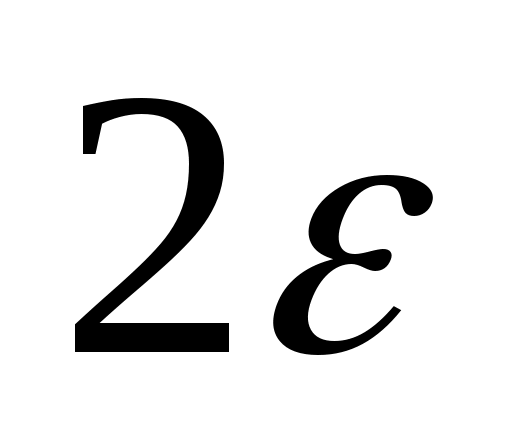 . Тогда координата середины отрезка и есть значение корня с требуемой точностью . Тогда координата середины отрезка и есть значение корня с требуемой точностью  . .
Метод бисекций – простой и надежный метод поиска простого корня* уравнения 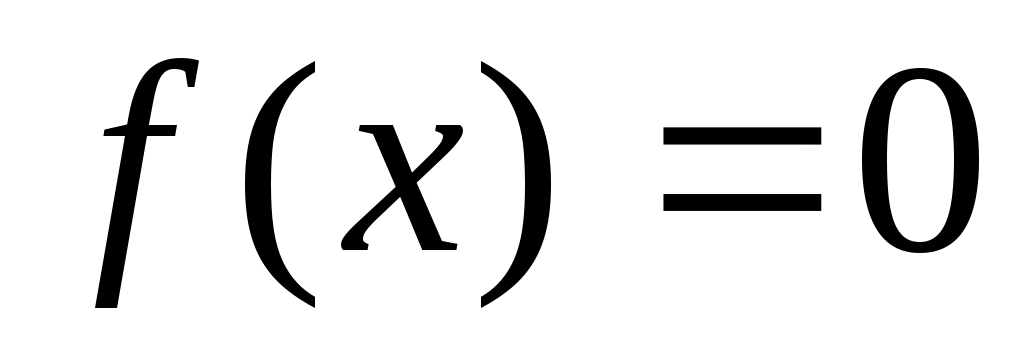 . Он сходится для любых непрерывных функций . Он сходится для любых непрерывных функций 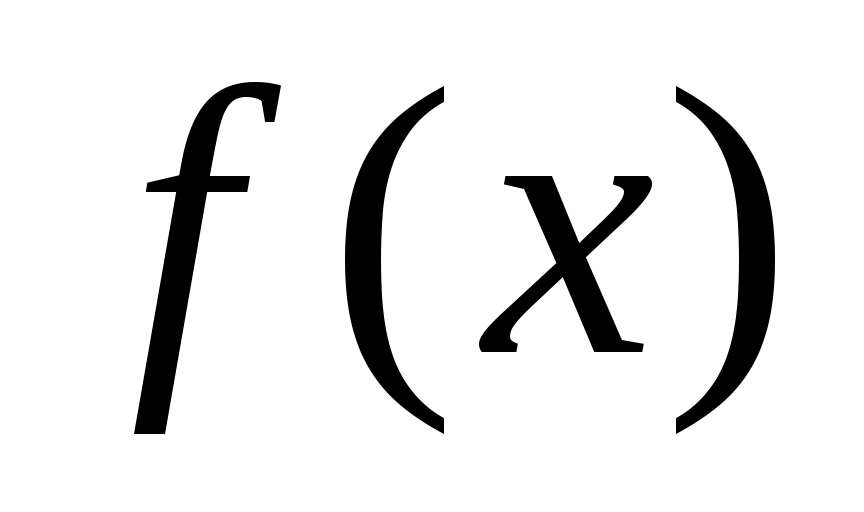 , в том числе недифференцируемых. Скорость сходимости невелика. Для достижения точности , в том числе недифференцируемых. Скорость сходимости невелика. Для достижения точности  необходимо совершить необходимо совершить  итераций, где итераций, где
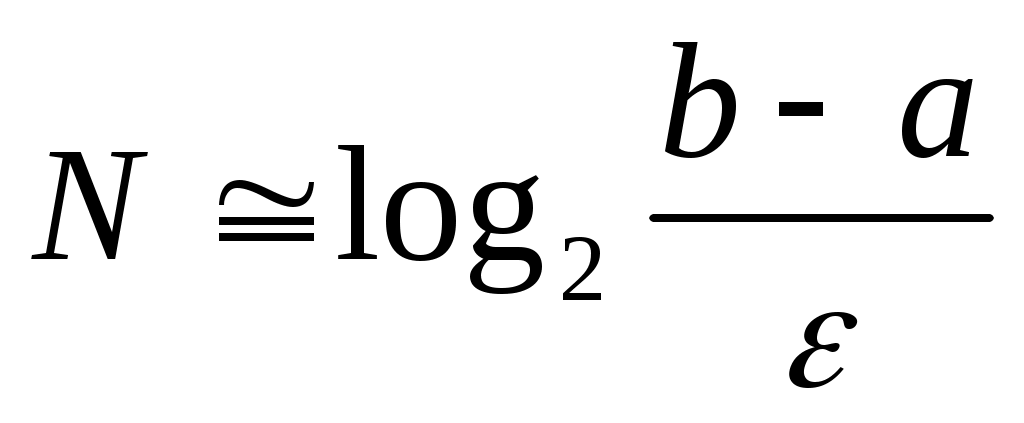 . .
Это означает, что для получения каждых трех верных десятичных знаков необходимо совершить около 10 итераций.
Если на отрезке 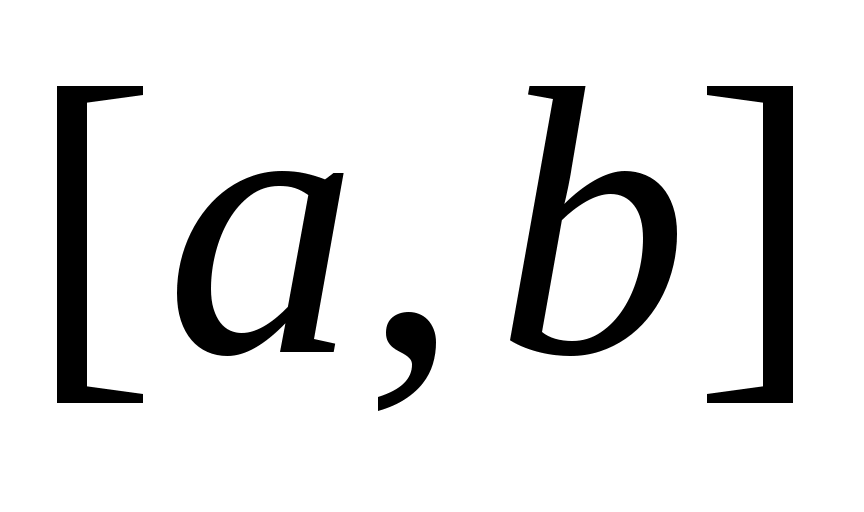 находится несколько корней уравнения находится несколько корней уравнения 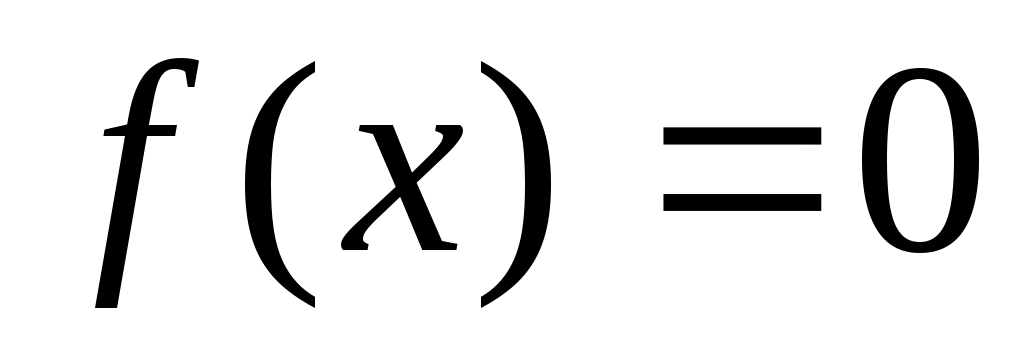 , то процесс сходится к одному из них. Метод неприменим для отыскания кратных корней четного порядка. В случае кратных корней нечетного порядка он менее точен. , то процесс сходится к одному из них. Метод неприменим для отыскания кратных корней четного порядка. В случае кратных корней нечетного порядка он менее точен.
Лабораторная работа №2 Решение системы нелинейных уравнений методом Ньютона
Рассмотрим систему 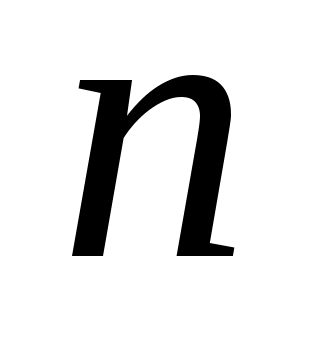 нелинейных уравнений с нелинейных уравнений с 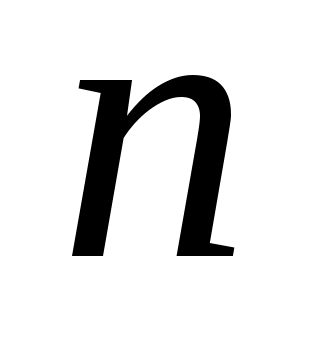 неизвестными неизвестными
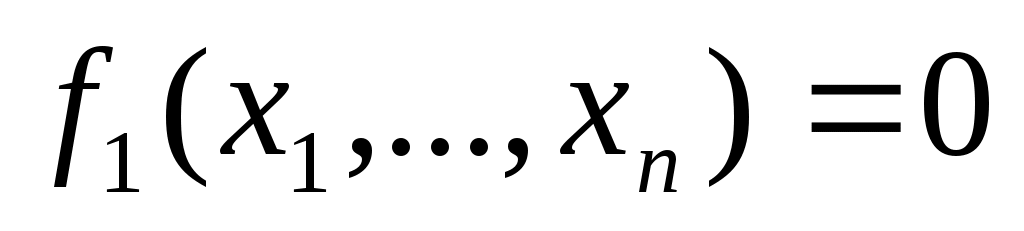 , ,
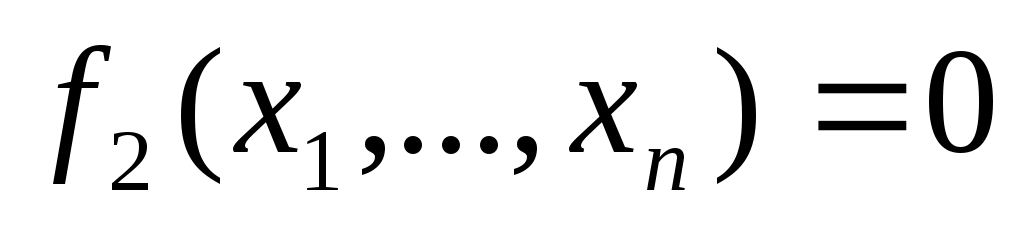 , (1) , (1)
……………….
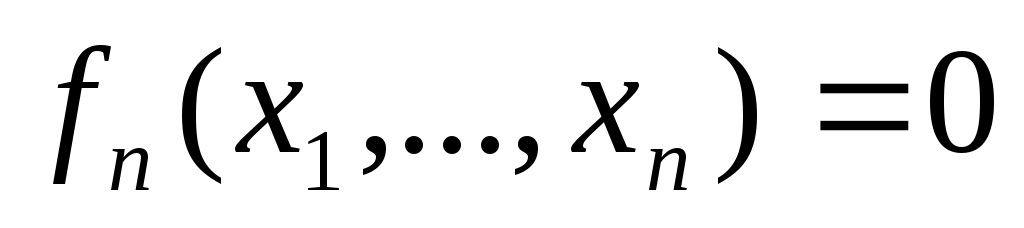
или в векторной форме
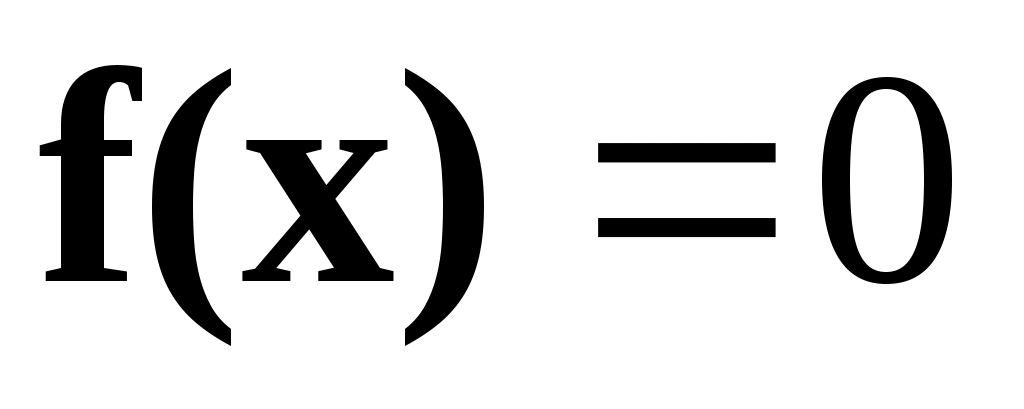 , (1’) , (1’)
где
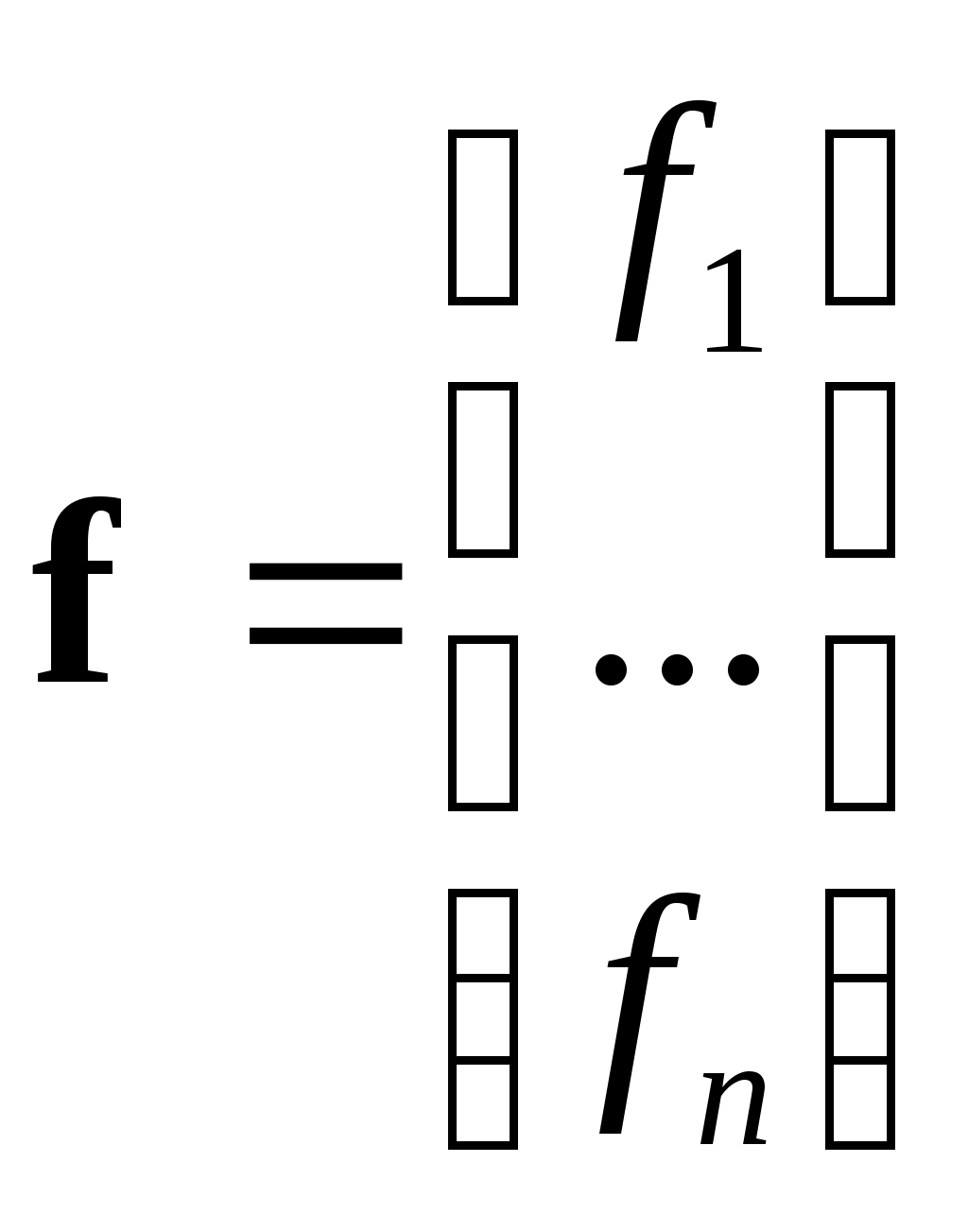 , , 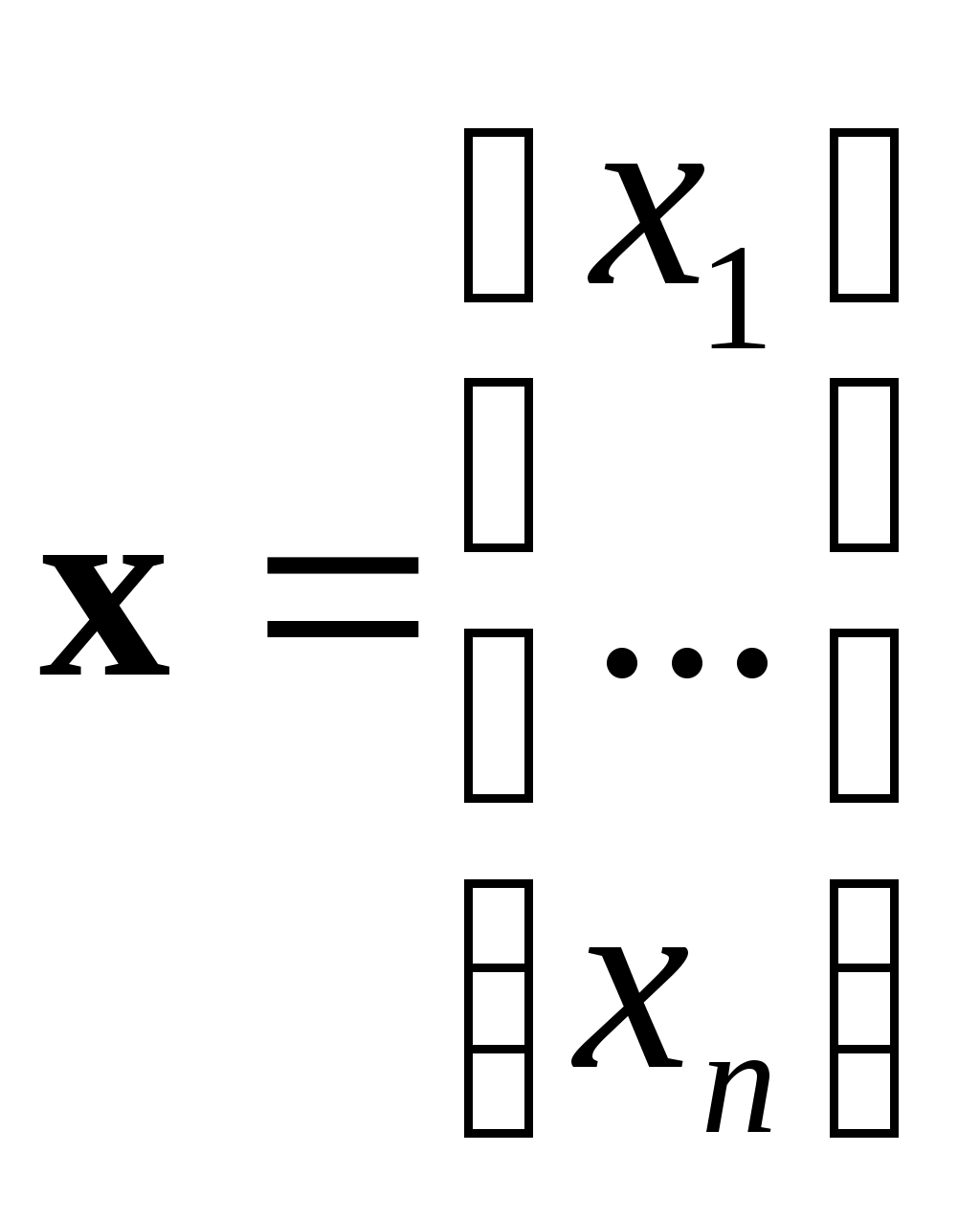 . .
Основная идея метода Ньютона состоит в выделении из уравнений системы линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем.
Пусть известно некоторое приближение 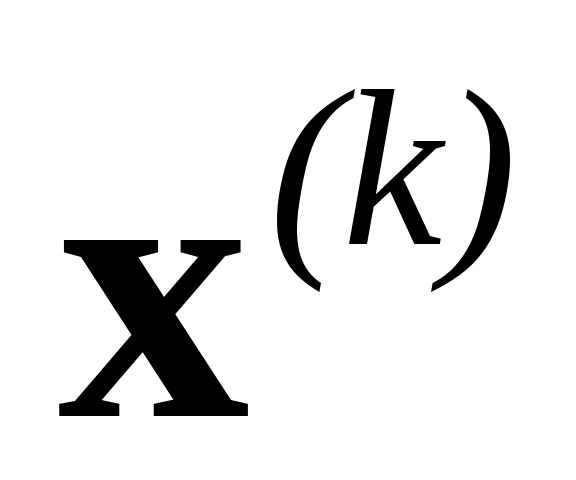 корня корня  . Тогда поправку . Тогда поправку 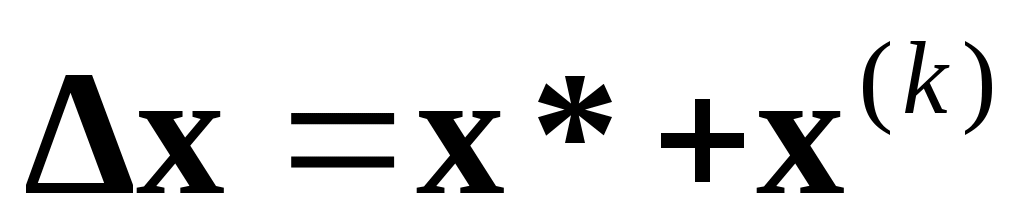 можно найти, решая систему можно найти, решая систему
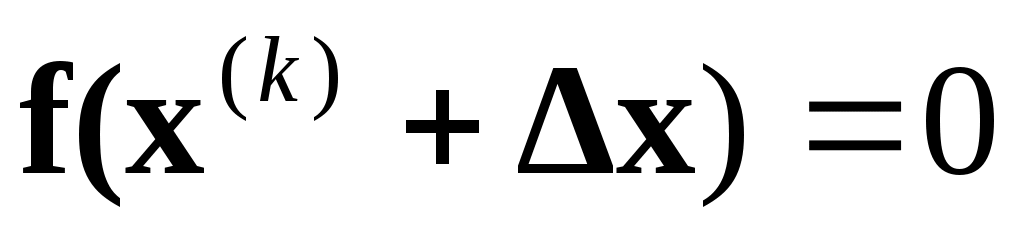 . .
Для определения  разложим векторную функцию разложим векторную функцию  в ряд по в ряд по 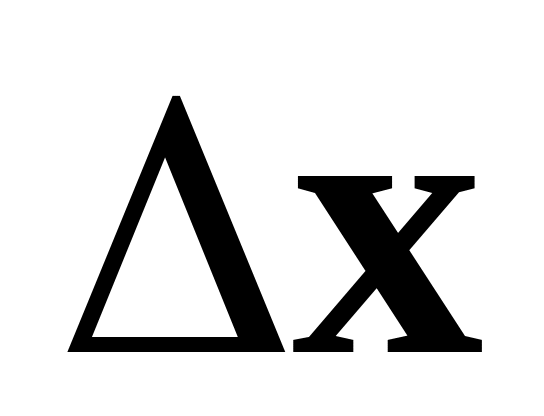 . Сохранив только линейные по . Сохранив только линейные по 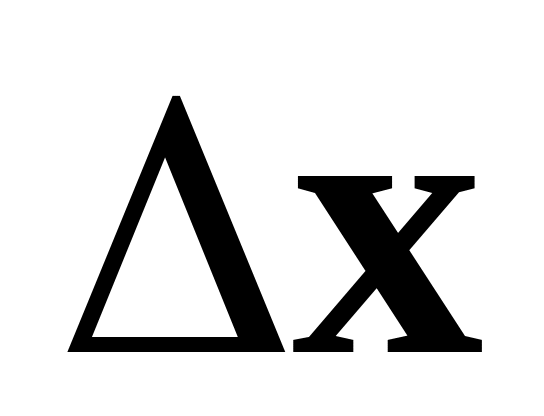 части, получим части, получим
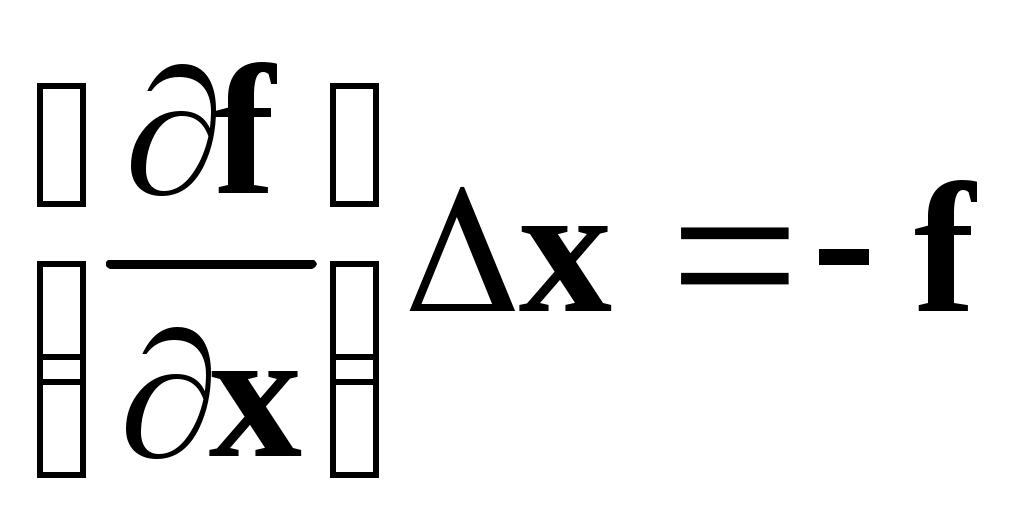 . .
Здесь через 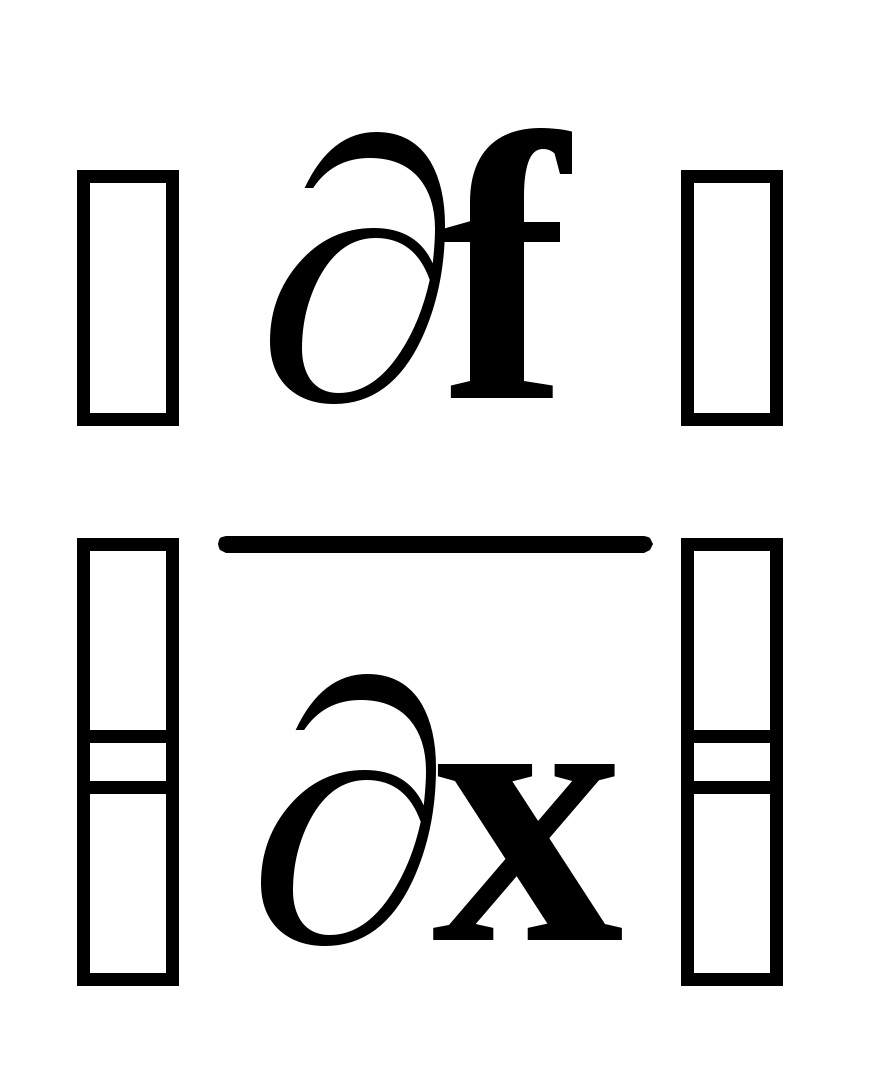 обозначена матрица производных обозначена матрица производных 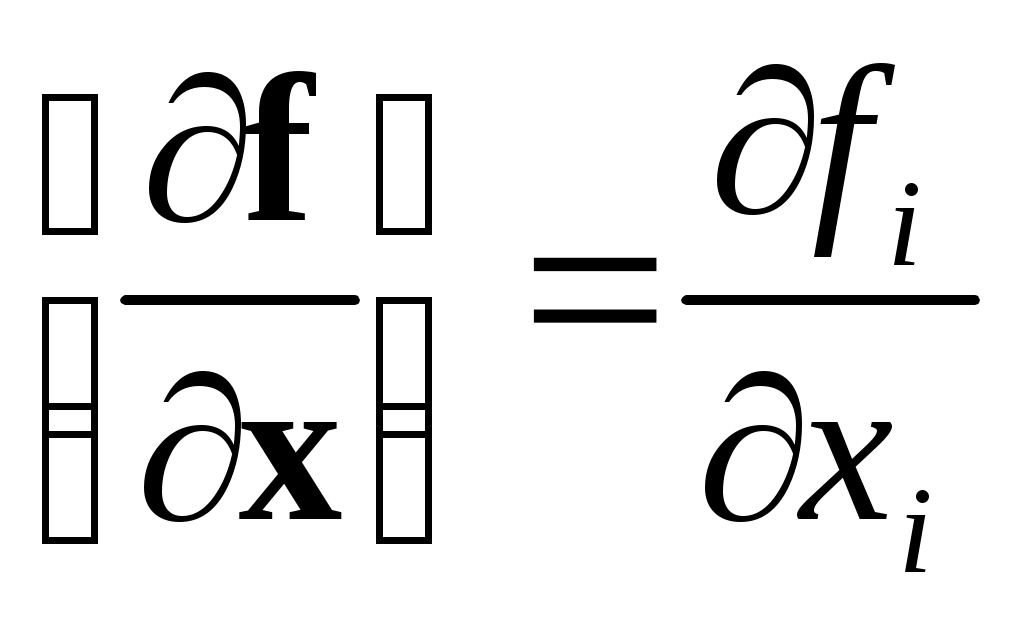 . .
Если 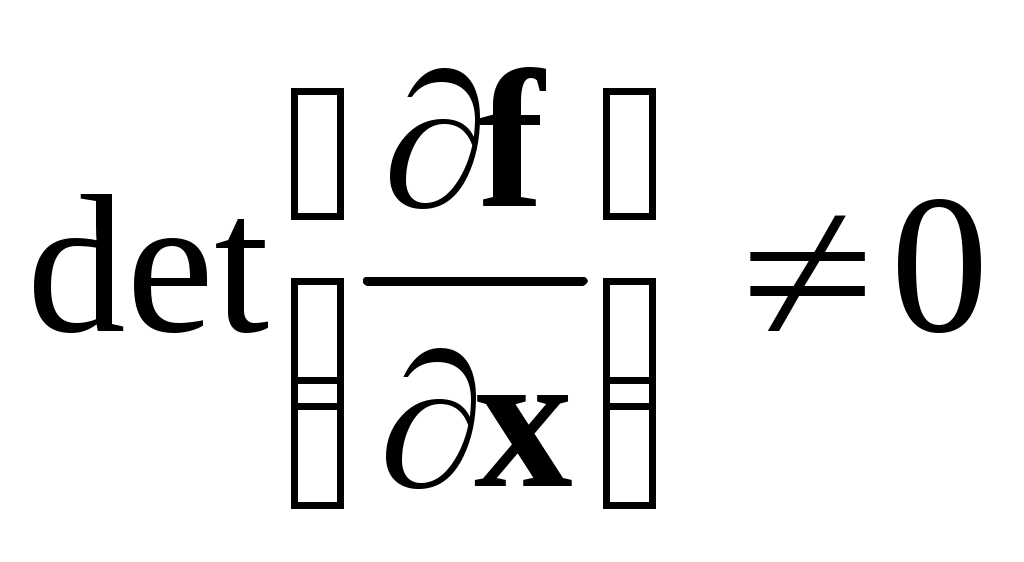 , то , то 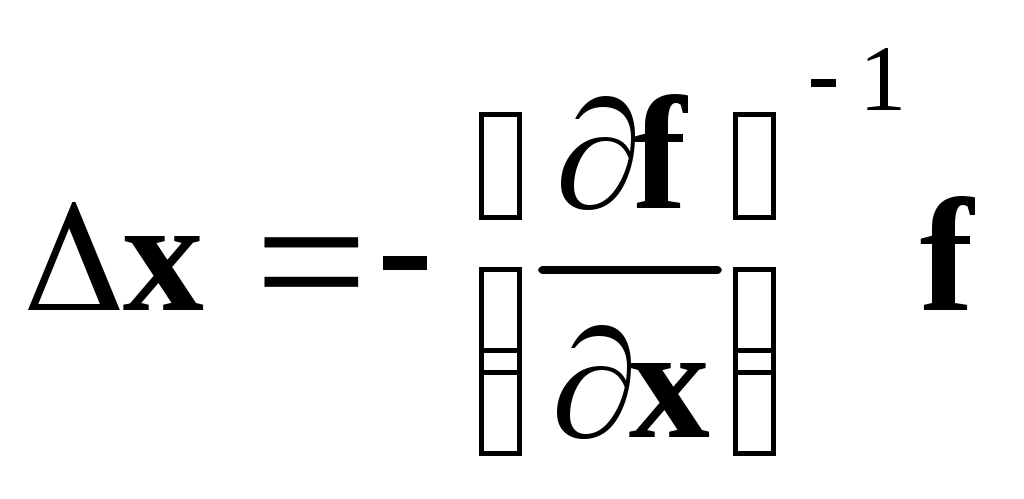 , где , где 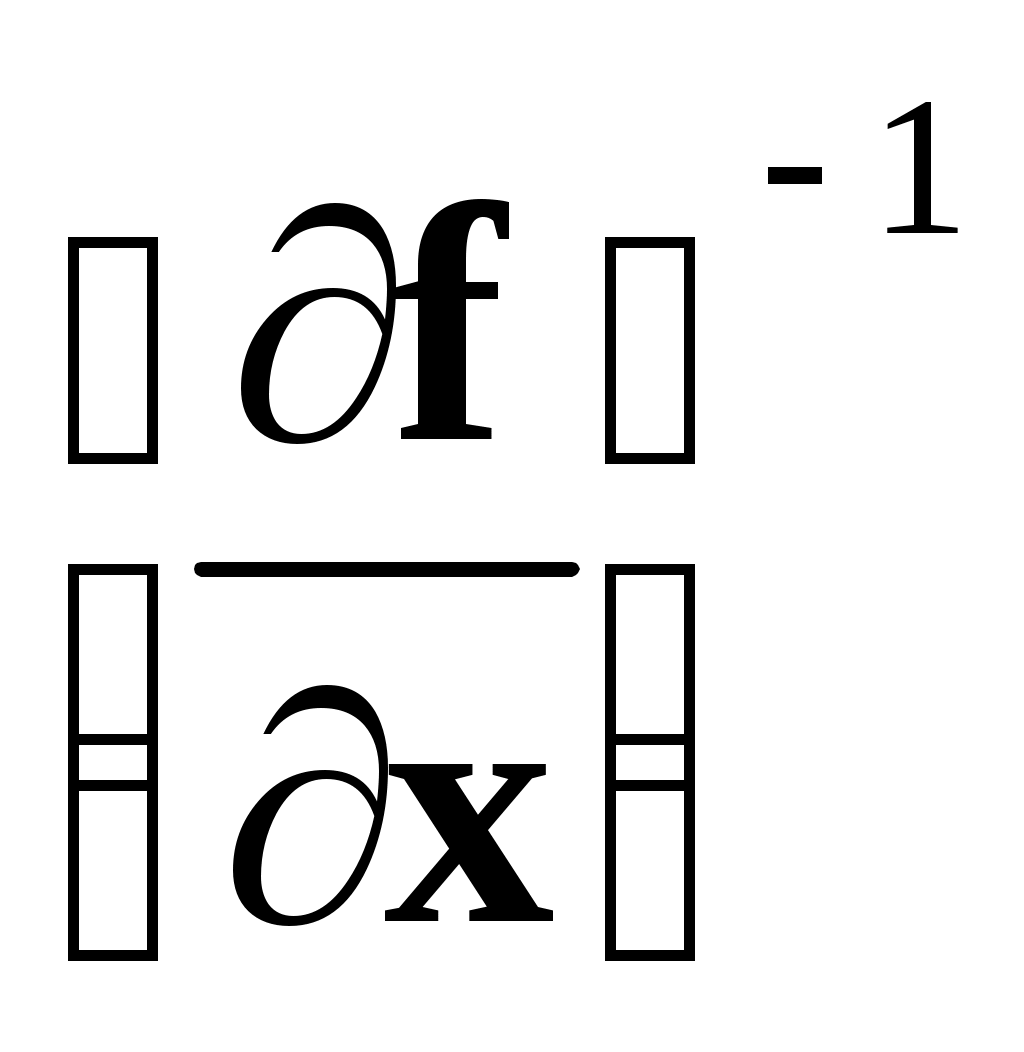 – матрица, обратная матрице производных. – матрица, обратная матрице производных.
Таким образом, последовательные приближения корня можно вычислять по формуле
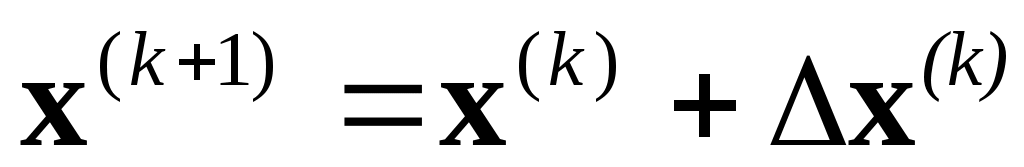 . .
Отсюда видно, что метод Ньютона решения системы (1) состоит в построении итерационной последовательности:
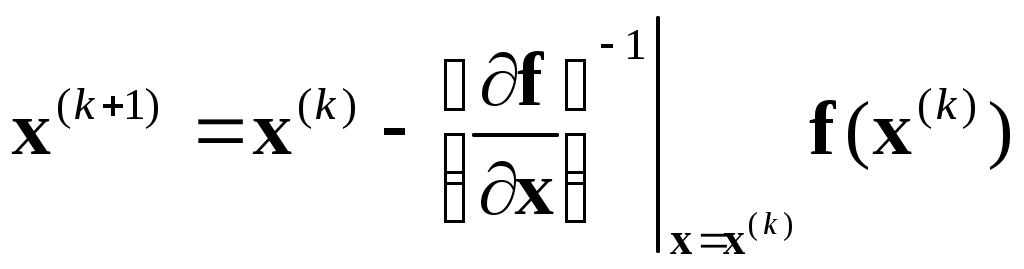 . (2) . (2)
Если 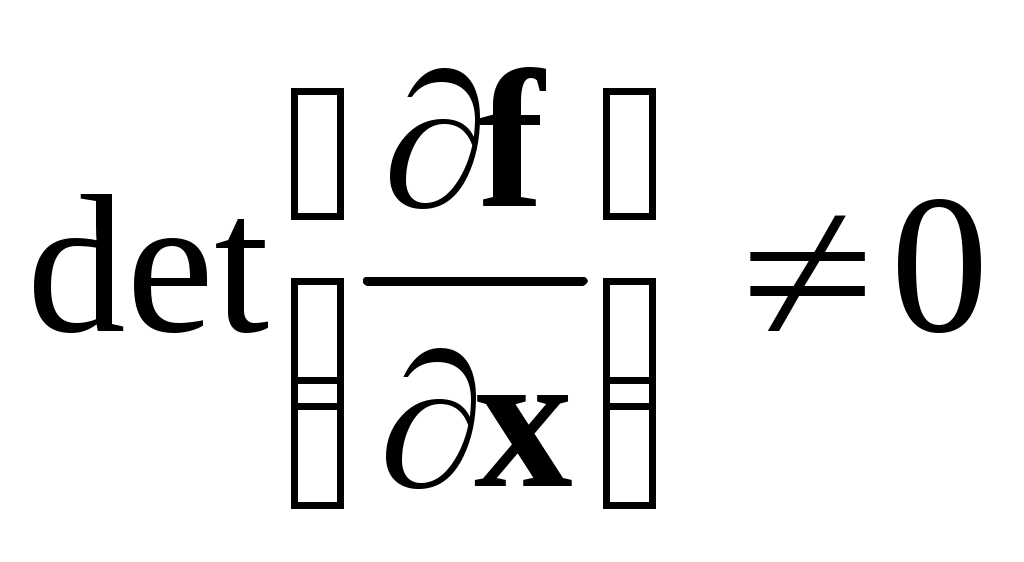 , то в достаточно малой окрестности корня , то в достаточно малой окрестности корня 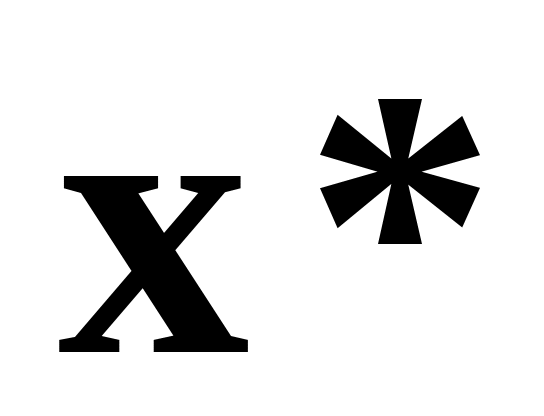 итерационный процесс (2) сходится, причем с квадратичной скоростью, т.е. если итерационный процесс (2) сходится, причем с квадратичной скоростью, т.е. если 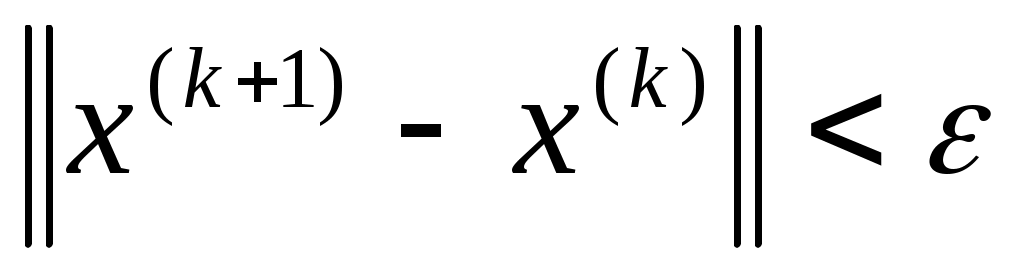 , то , то 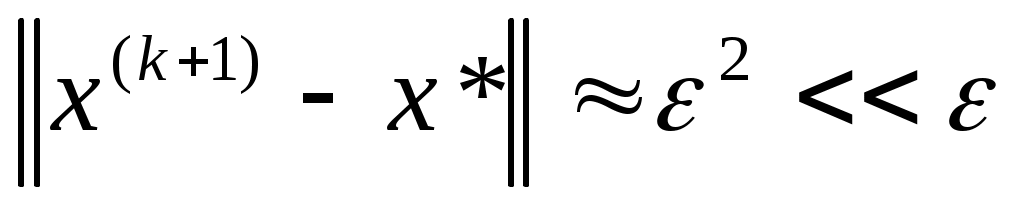 . Поэтому в качестве критерия окончания итерационного процесса можно использовать условие . Поэтому в качестве критерия окончания итерационного процесса можно использовать условие 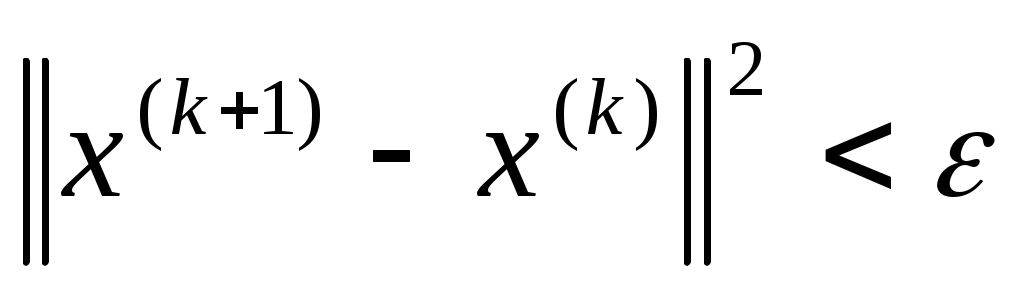 . Если начальное приближение выбрано удачно, то метод Ньютона сходится очень быстро. . Если начальное приближение выбрано удачно, то метод Ньютона сходится очень быстро.
Лабораторная работа №3 Решение системы линейных уравнений методом Гаусса
Методом Гаусса называют точный*) метод решения невырожденной системы линейных уравнений, состоящий в том, что последовательным исключением неизвестных систему
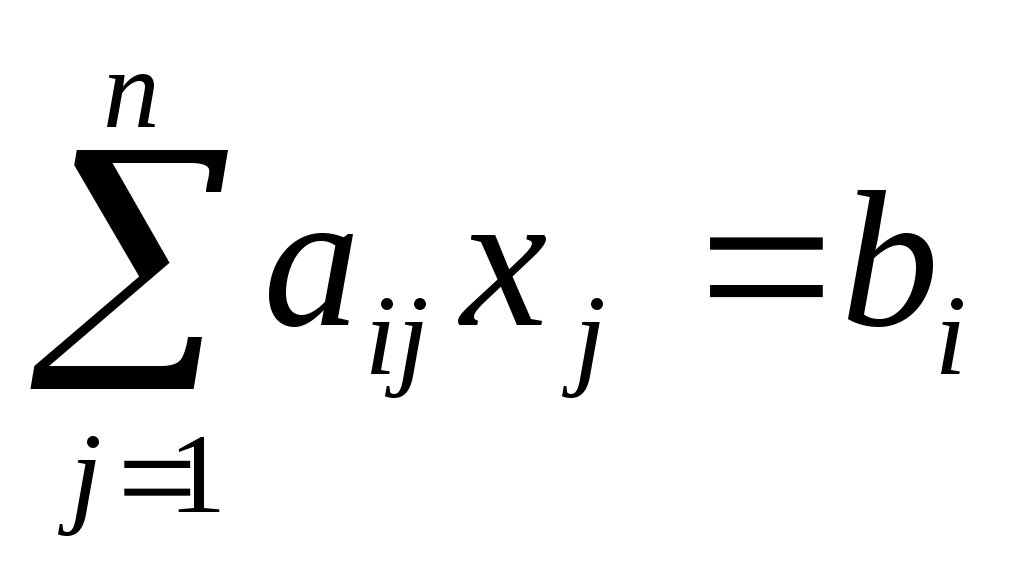 , , 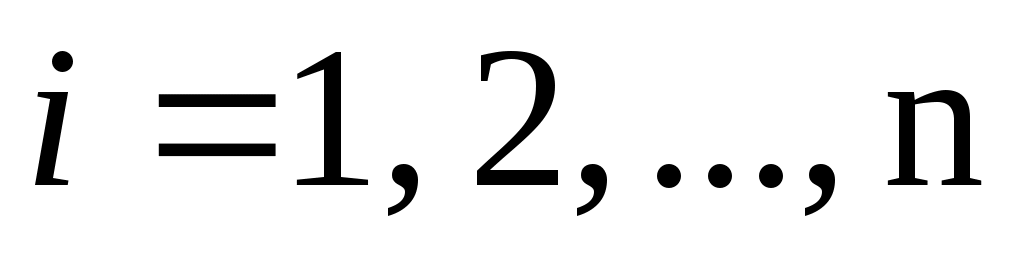 , ,
приводят к эквивалентной системе с треугольной матрицей
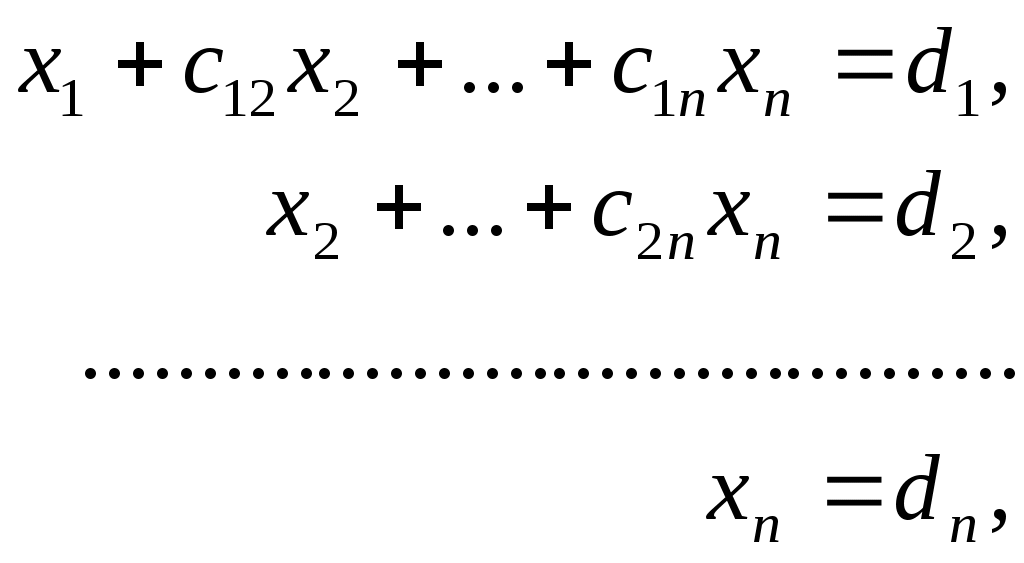
решение которой находят по рекуррентным формулам
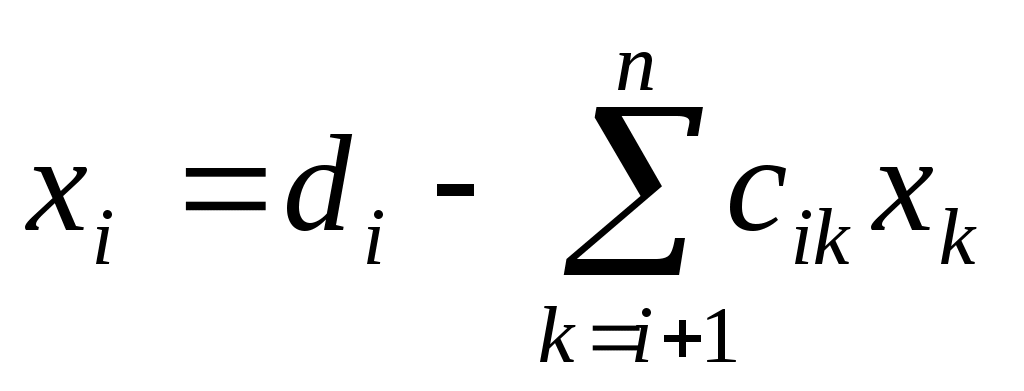 , , 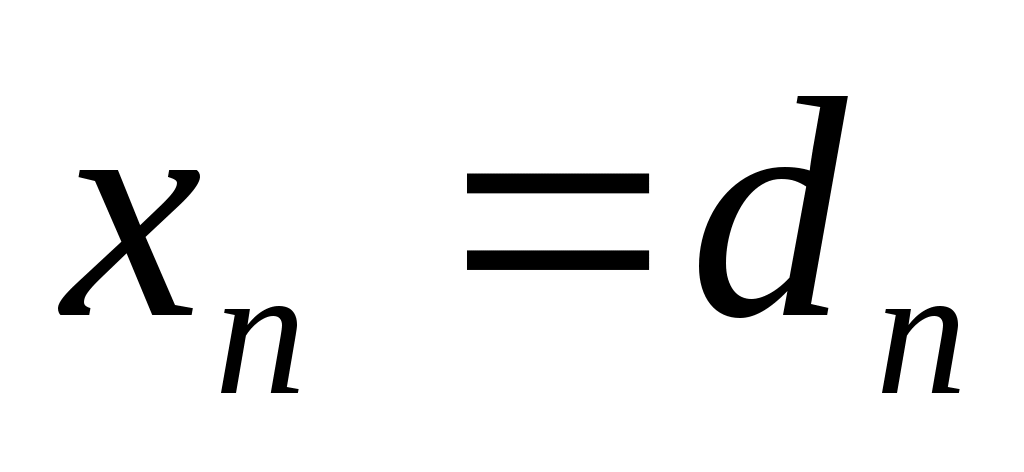 , , 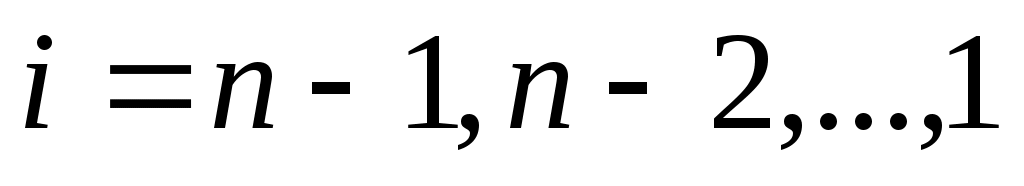 . .
Существует много вариантов этого метода. Рассмотрим схему с выбором главного элемента. Пусть исходная система имеет вид
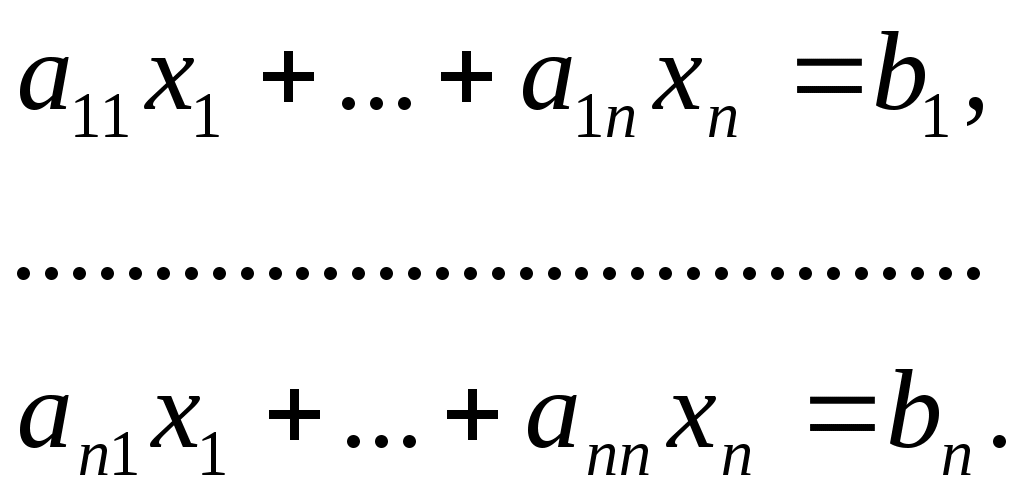 (1) (1)
Предположим, что 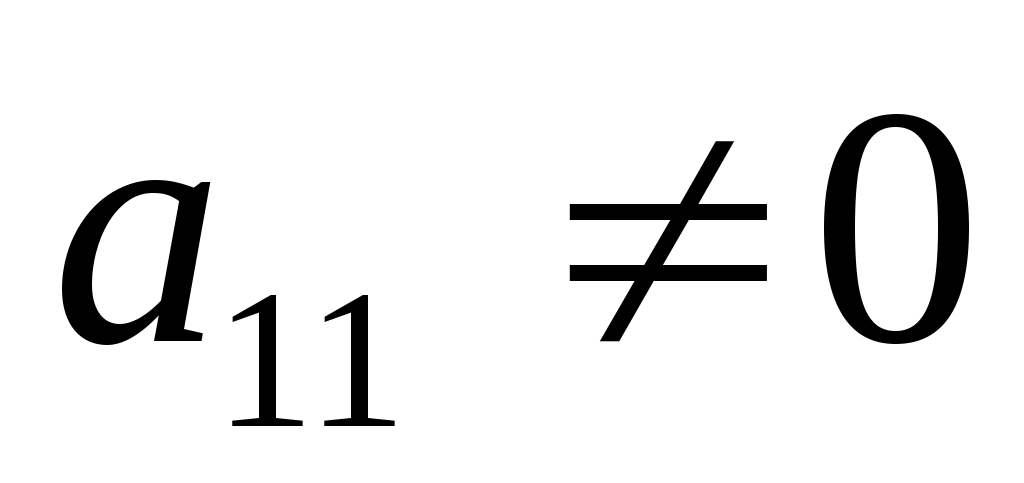 , и разделим обе части первого уравнения системы на , и разделим обе части первого уравнения системы на  . В результате получим . В результате получим
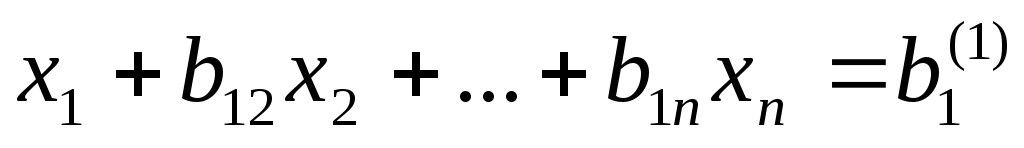 , (2) , (2)
где 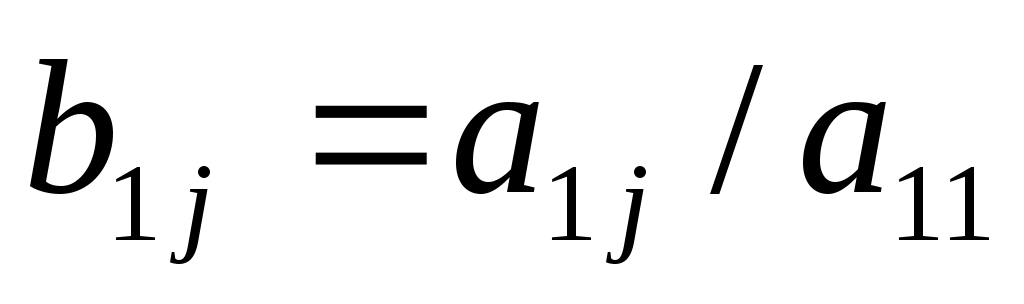 , , 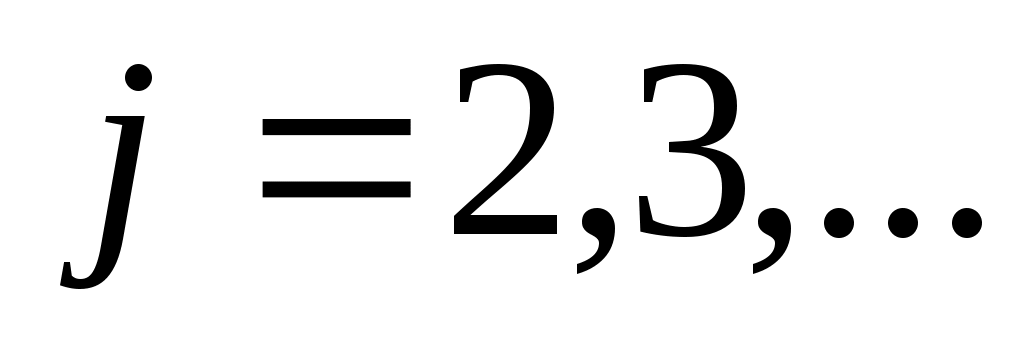 , , 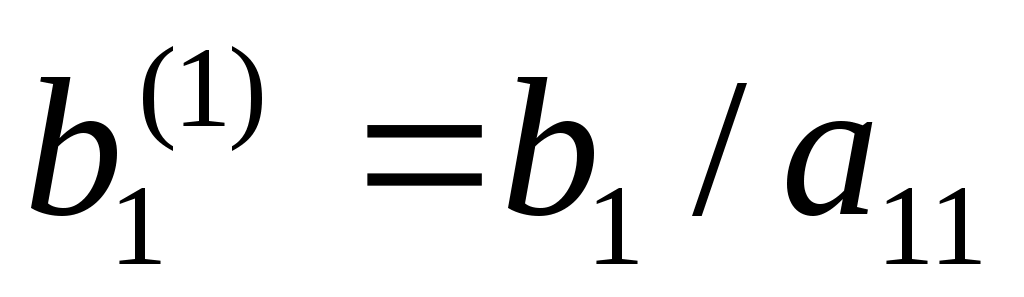 . С помощью уравнения (2) исключим во всех уравнениях системы (1), начиная со второго, слагаемые, содержащие . С помощью уравнения (2) исключим во всех уравнениях системы (1), начиная со второго, слагаемые, содержащие 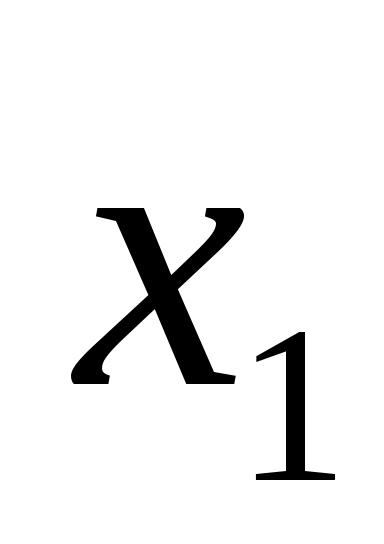 . Для этого умножаем обе части уравнения (2) последовательно на . Для этого умножаем обе части уравнения (2) последовательно на 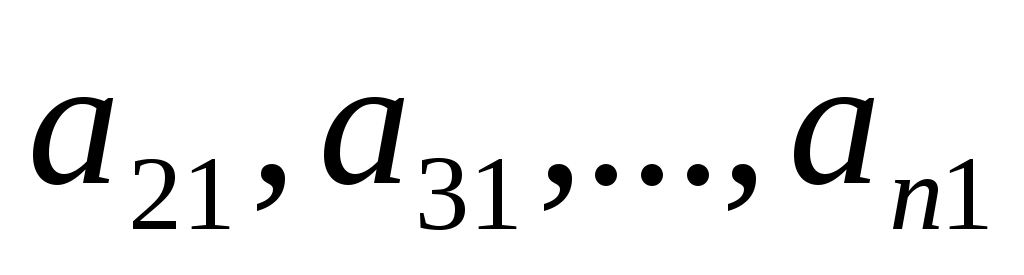 и вычитаем соответственно из второго, третьего, …, n–го уравнения системы (1). В результате получаем систему, порядок которой на единицу меньше порядка исходной системы: и вычитаем соответственно из второго, третьего, …, n–го уравнения системы (1). В результате получаем систему, порядок которой на единицу меньше порядка исходной системы:
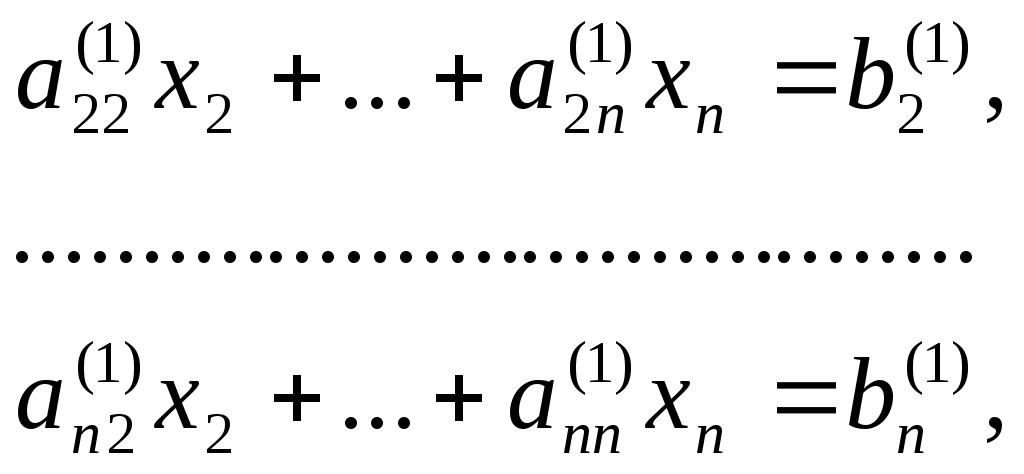
где 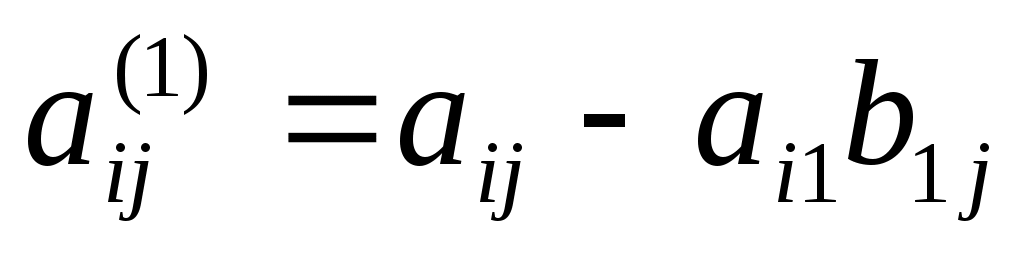 , , 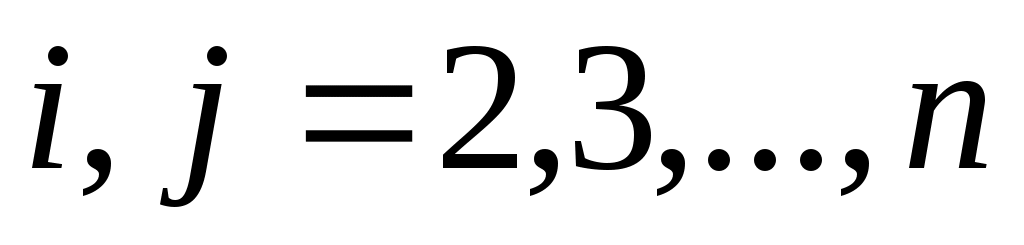 , , 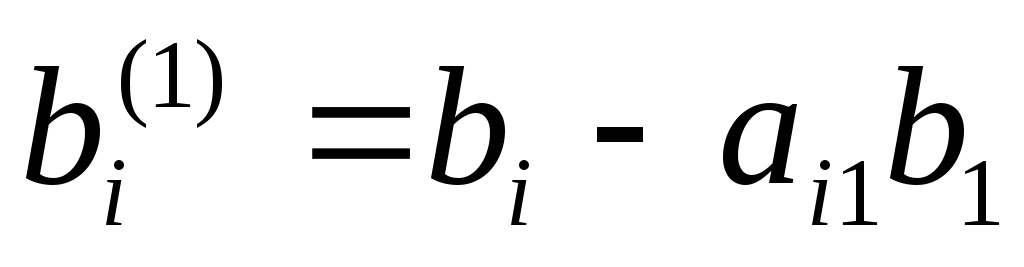 , , 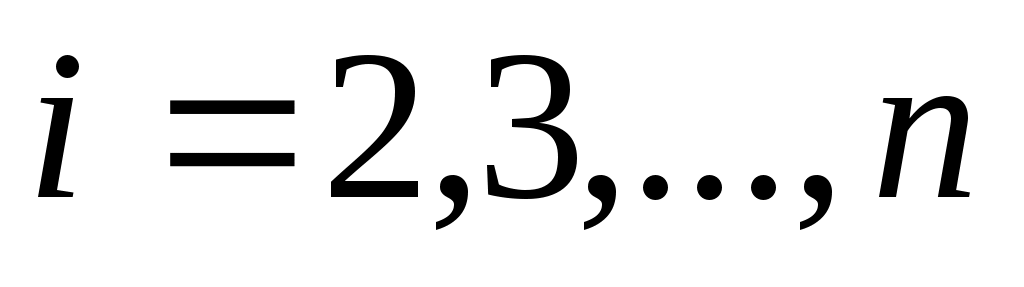 . .
Аналогично преобразуем полученную систему. В результате кратного повторения этого преобразования получим систему с треугольной матрицей
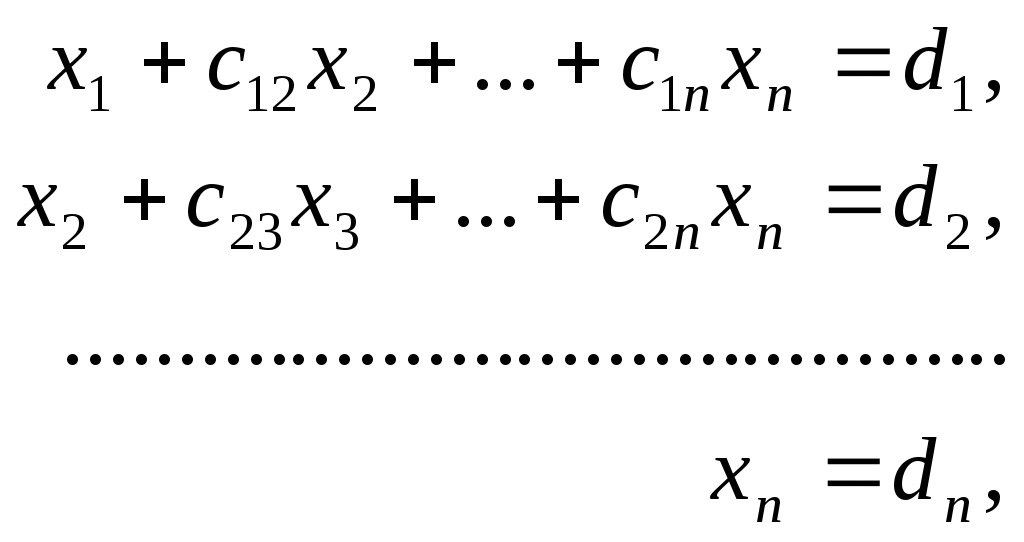 (3) (3)
которая эквивалентна системе (1) и легко решается. В самом деле, из последнего уравнения находим 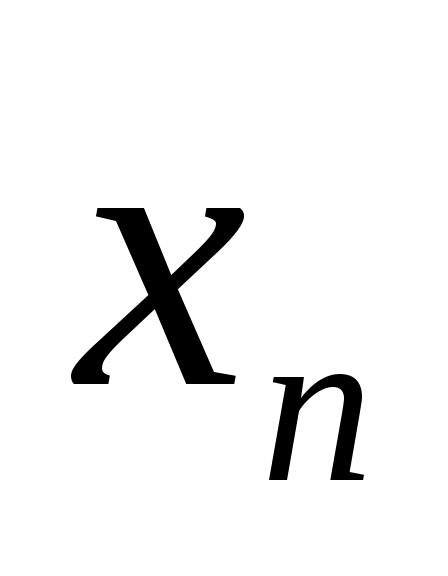 , подставляя , подставляя 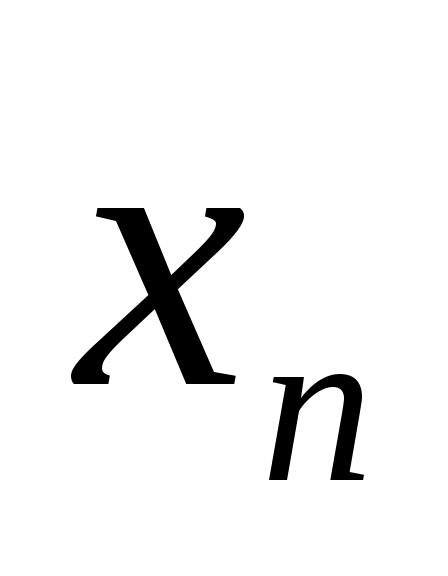 в предпоследнее уравнение, найдем в предпоследнее уравнение, найдем 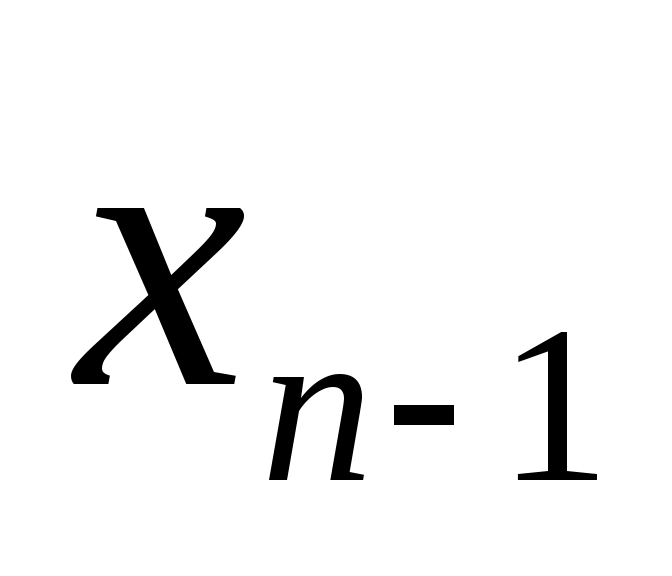 , затем , затем 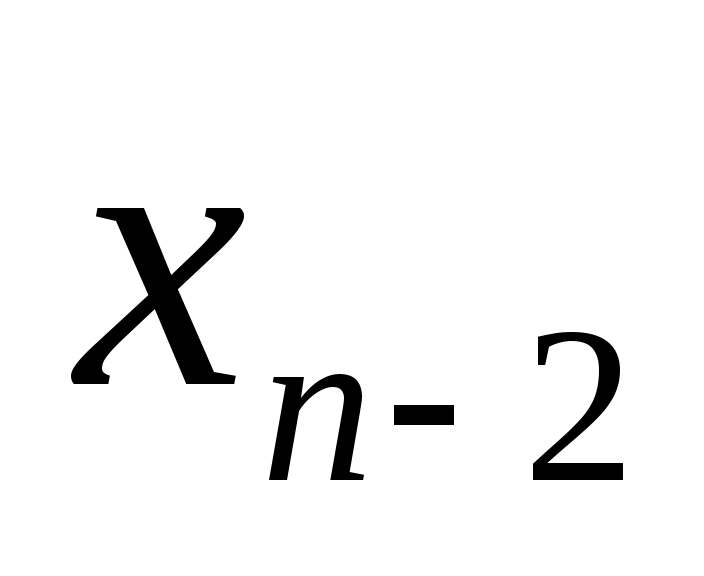 и т.д. до и т.д. до 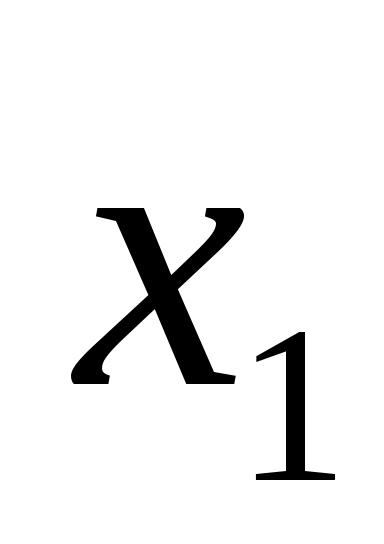 , которое находим из первого уравнения системы, когда уже известны , которое находим из первого уравнения системы, когда уже известны 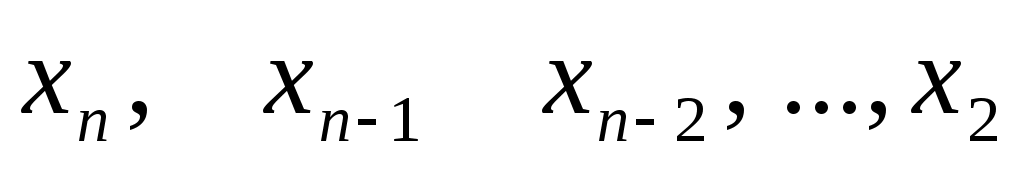 . .
Таким образом, вычисления по методу Гаусса распадаются на два этапа: на первом этапе, называемом прямым ходом метода, исходную систему преобразуют к треугольному виду. На втором этапе, который называют обратным ходом, решают треугольную систему (3), эквивалентную исходной.
Коэффициенты 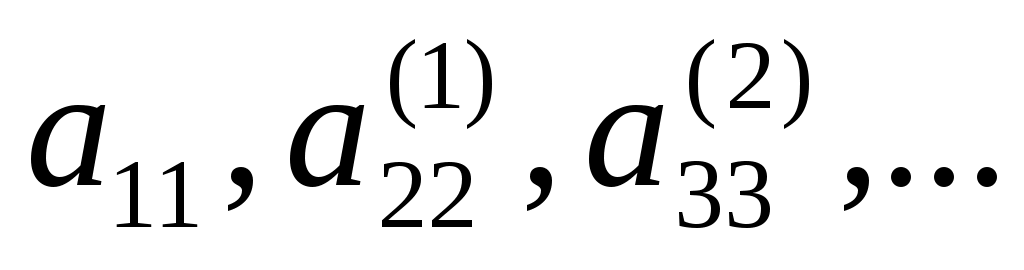 называют ведущими элементами метода Гаусса. На каждом шаге предполагалось, что называют ведущими элементами метода Гаусса. На каждом шаге предполагалось, что 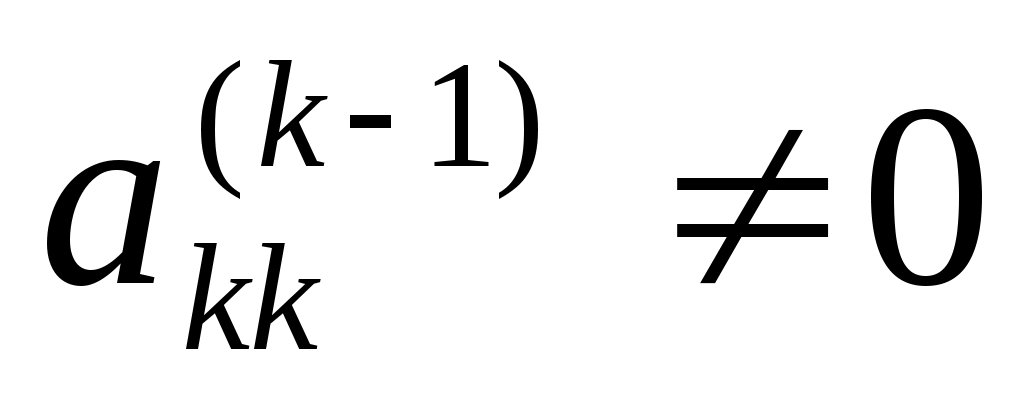 . Если окажется, что это не так, то в качестве ведущего элемента можно использовать любой другой ненулевой коэффициент системы. Однако если коэффициент . Если окажется, что это не так, то в качестве ведущего элемента можно использовать любой другой ненулевой коэффициент системы. Однако если коэффициент 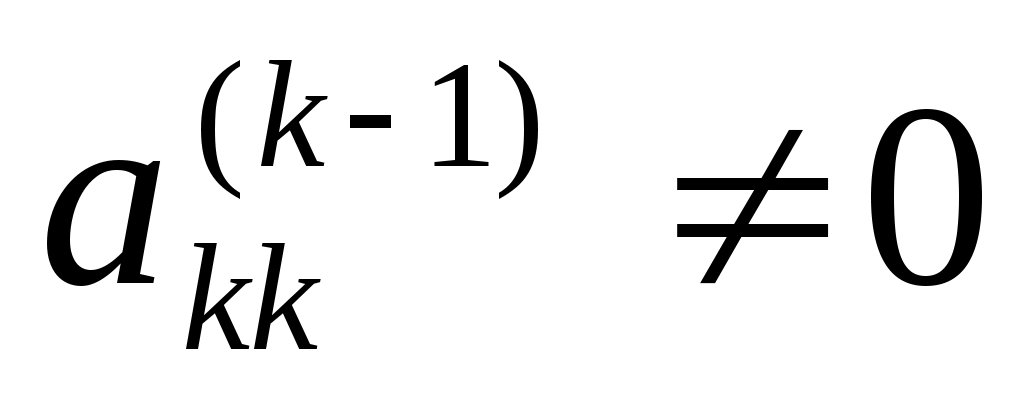 мал, то после деления на этот элемент и вычитания мал, то после деления на этот элемент и вычитания 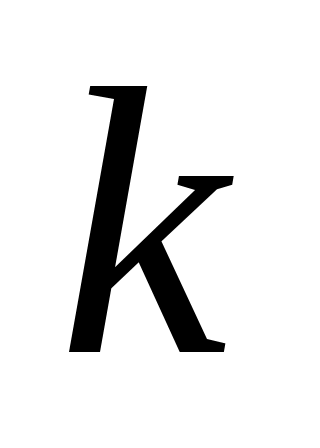 -го уравнения из последующий возникают большие погрешности округления. Чтобы избежать этого, на каждом этапе уравнения переставляют так, чтобы на главной диагонали оказался наибольший по модулю элемент -го уравнения из последующий возникают большие погрешности округления. Чтобы избежать этого, на каждом этапе уравнения переставляют так, чтобы на главной диагонали оказался наибольший по модулю элемент 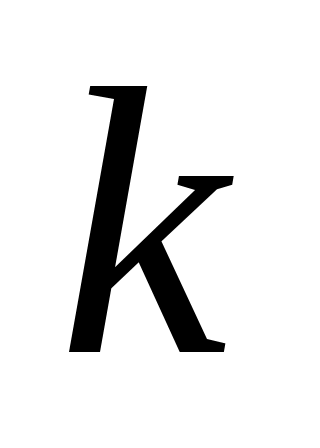 -го столбца. Если матрица системы хорошо обусловлена*), то в методе Гаусса с выбором главного элемента погрешности округления невелики. Одновременно с решением системы можно найти определитель матрицы системы. Нетрудно убедиться, что определитель матрицы системы равен произведению ведущих элементов, т.е. -го столбца. Если матрица системы хорошо обусловлена*), то в методе Гаусса с выбором главного элемента погрешности округления невелики. Одновременно с решением системы можно найти определитель матрицы системы. Нетрудно убедиться, что определитель матрицы системы равен произведению ведущих элементов, т.е.  . .
Лабораторная работа №4 Численное интегрирование
Пусть требуется найти определенный интеграл
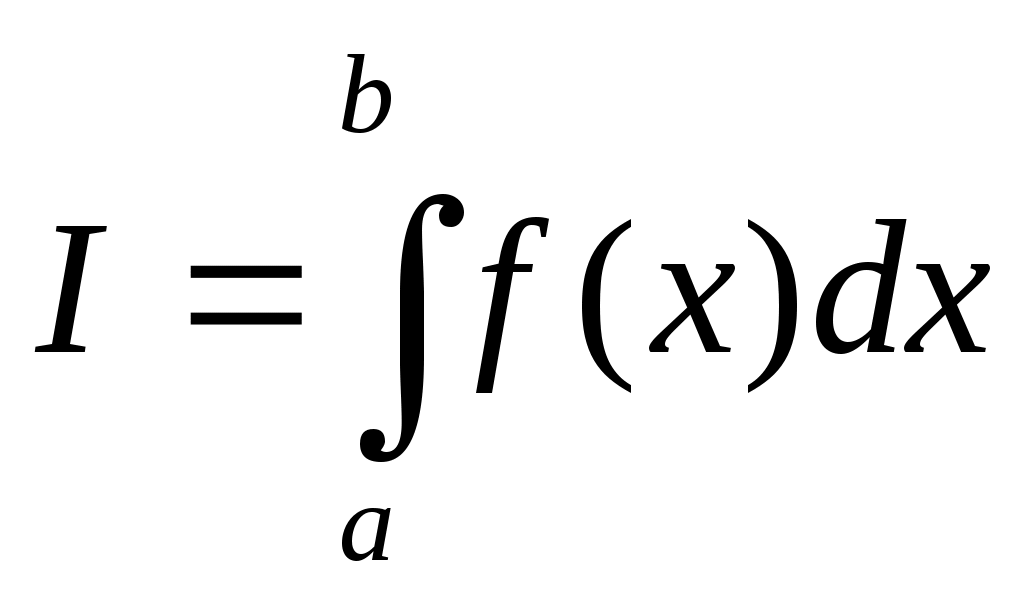 , ,
где функция 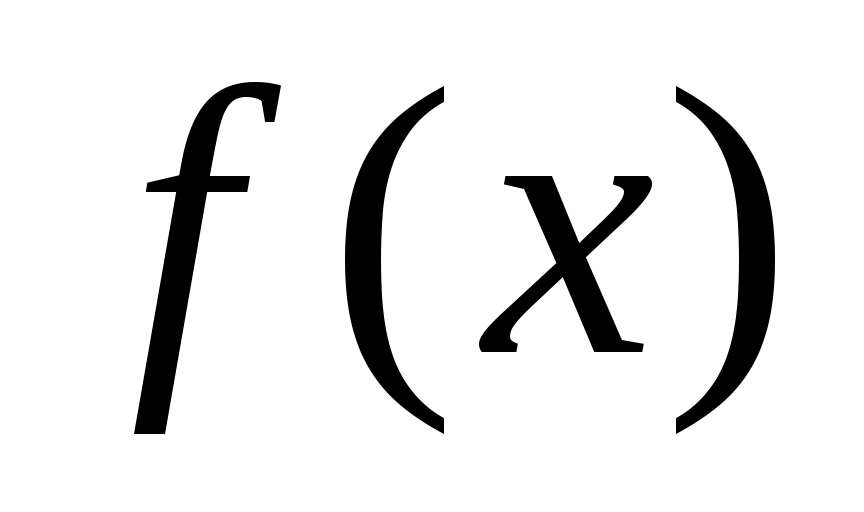 непрерывна на отрезке непрерывна на отрезке 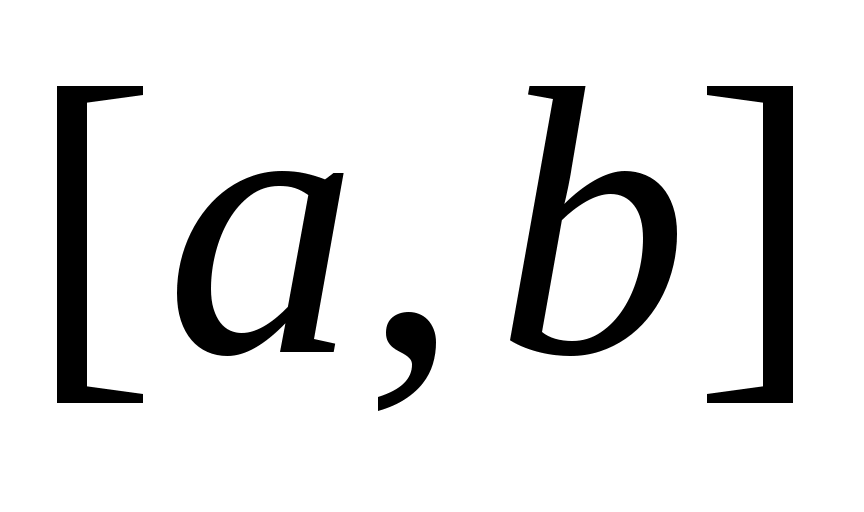 . .
Для приближенного вычисления интегралов чаще всего подынтегральную функцию заменяют «близкой» ей вспомогательной функцией, интеграл от которой вычисляется аналитически. За приближенное значение интеграла принимают значение интеграла от вспомогательной функции.
Заменим функцию на отрезке 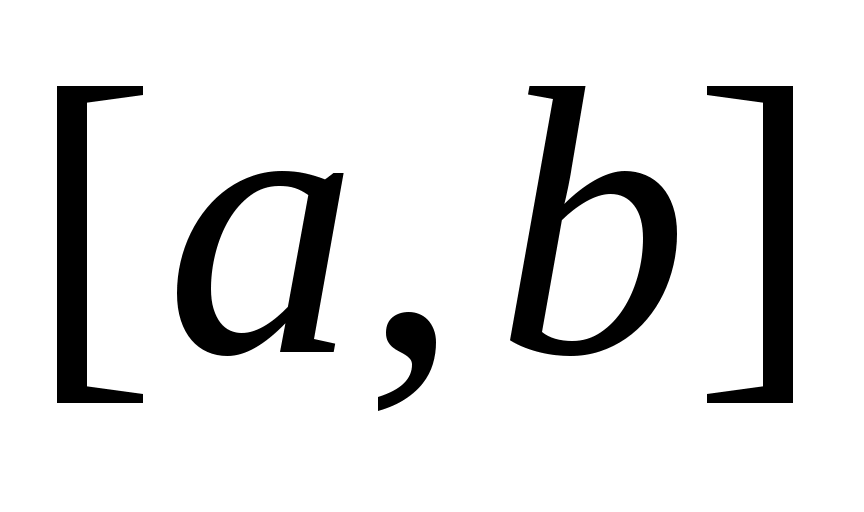 ее значением в середине отрезка. Искомый интеграл, равный площади криволинейной фигуры, заменяется на площадь прямоугольника. Из геометрических соображений нетрудно записать формулу прямоугольников ее значением в середине отрезка. Искомый интеграл, равный площади криволинейной фигуры, заменяется на площадь прямоугольника. Из геометрических соображений нетрудно записать формулу прямоугольников
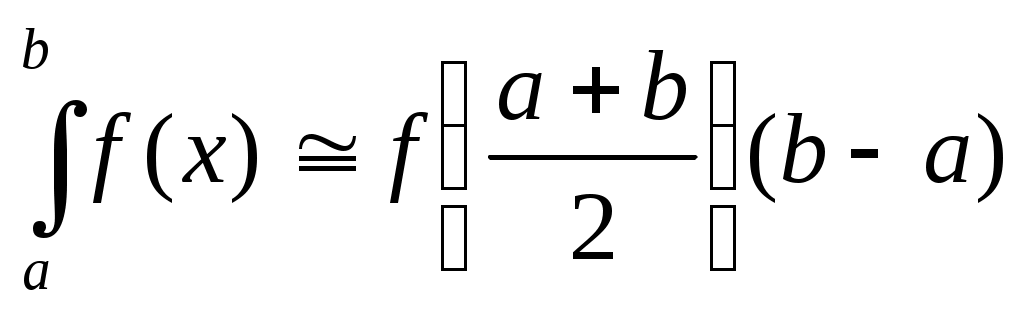 . .
Приблизив 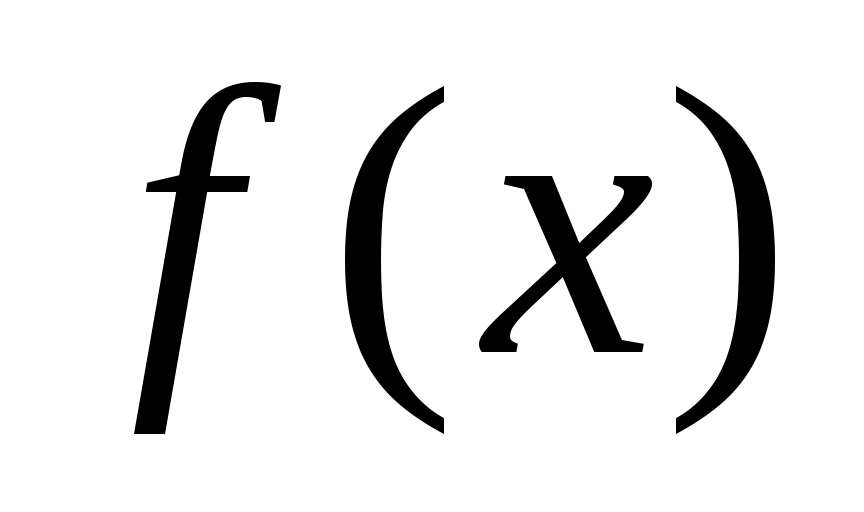 линейной функцией и вычислив площадь соответствующей трапеции, получим формулу трапеций линейной функцией и вычислив площадь соответствующей трапеции, получим формулу трапеций
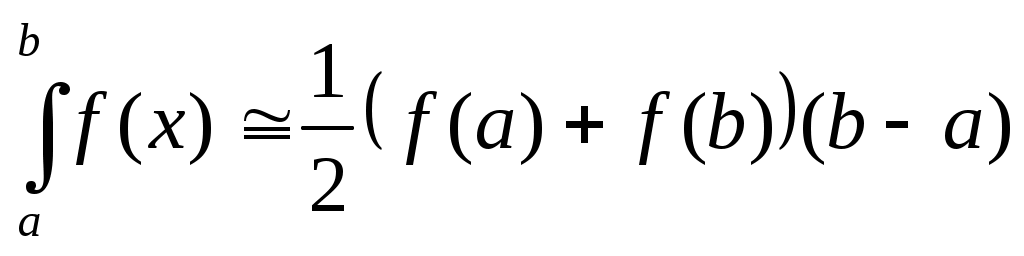 . .
Если же приблизить подынтегральную функцию параболой, проходящей через точки 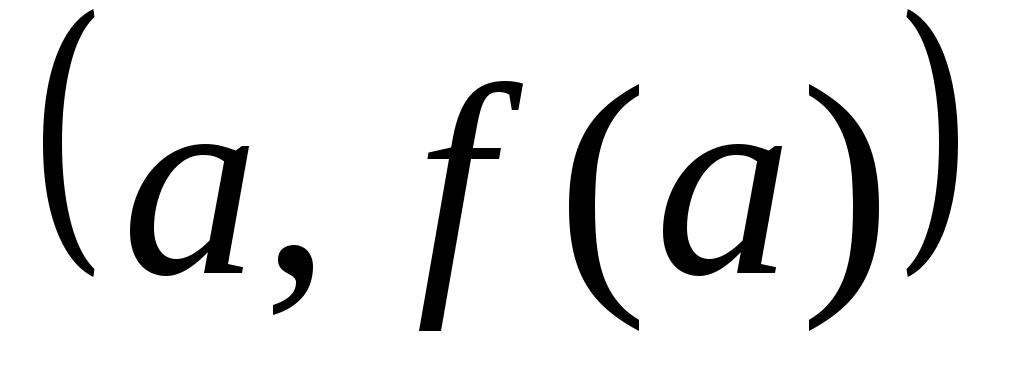 , , 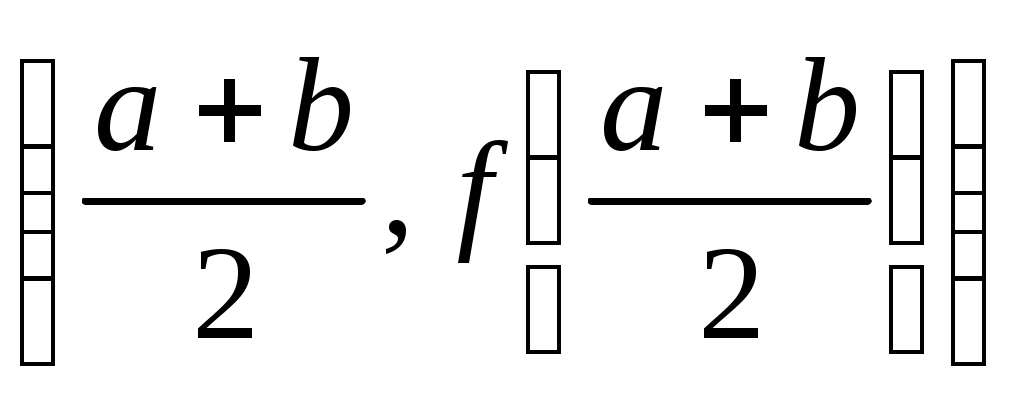 , , 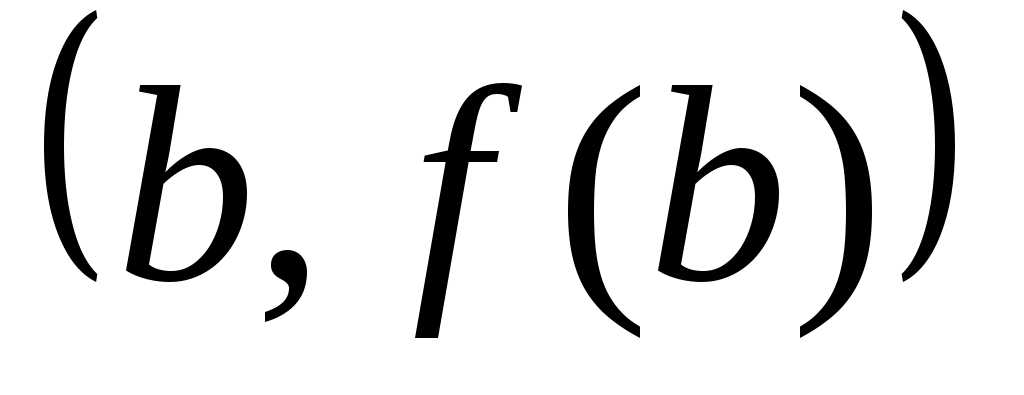 , то получим формулу Симпсона , то получим формулу Симпсона
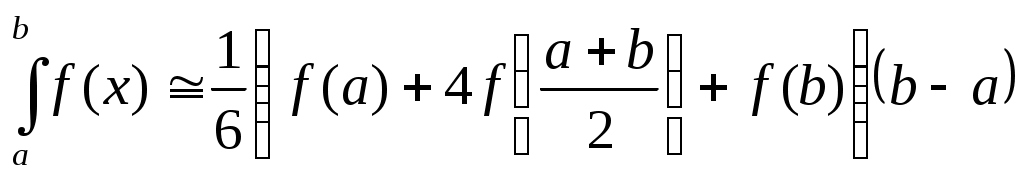 . .
Все три формулы хорошо иллюстрируются геометрически (рис. 2).
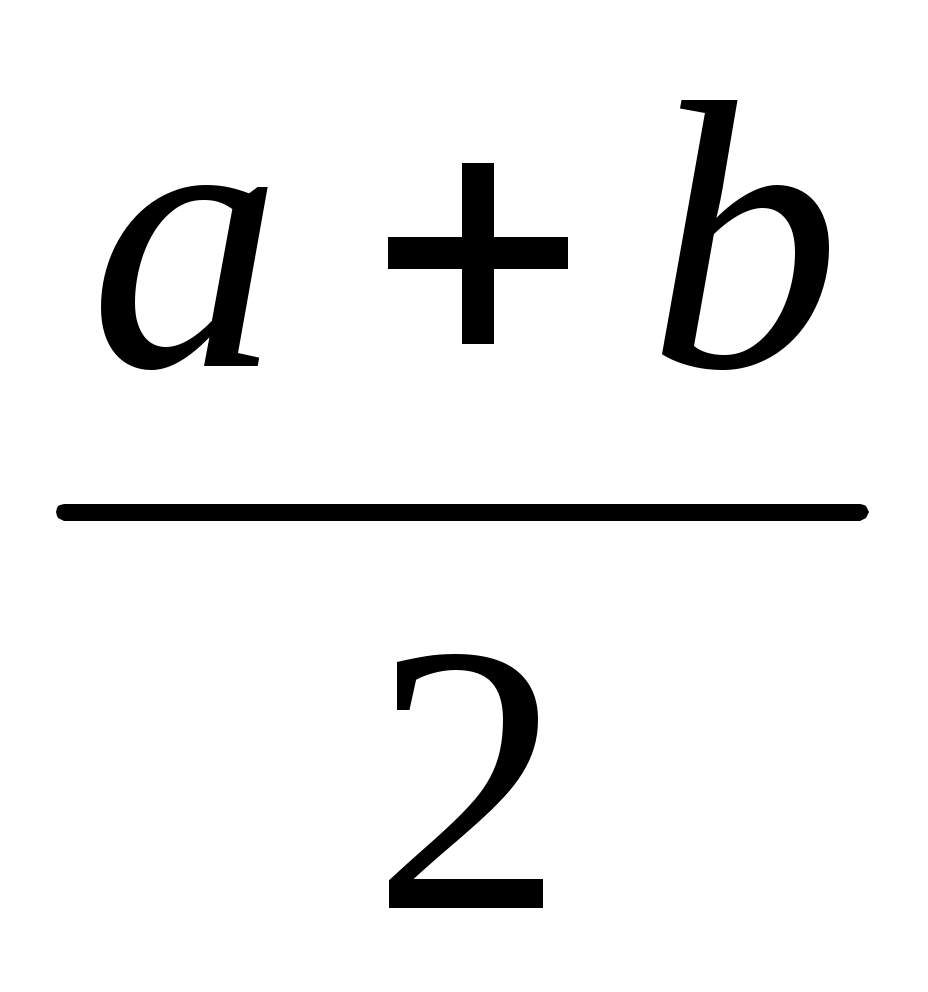

0
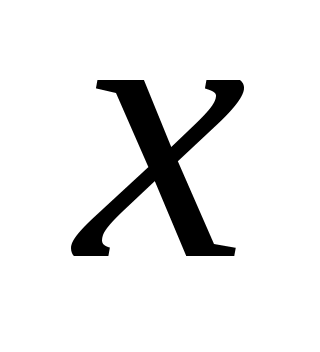
      


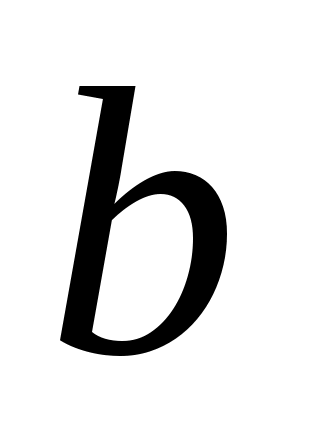
Рис.2.
Для повышения точности интегрирования применяют составные формулы. Для этого разбивают отрезок 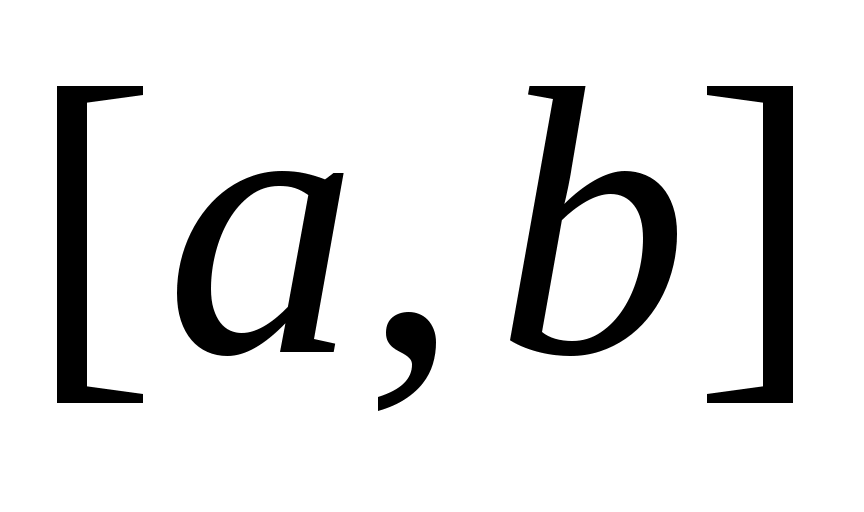 на четное на четное 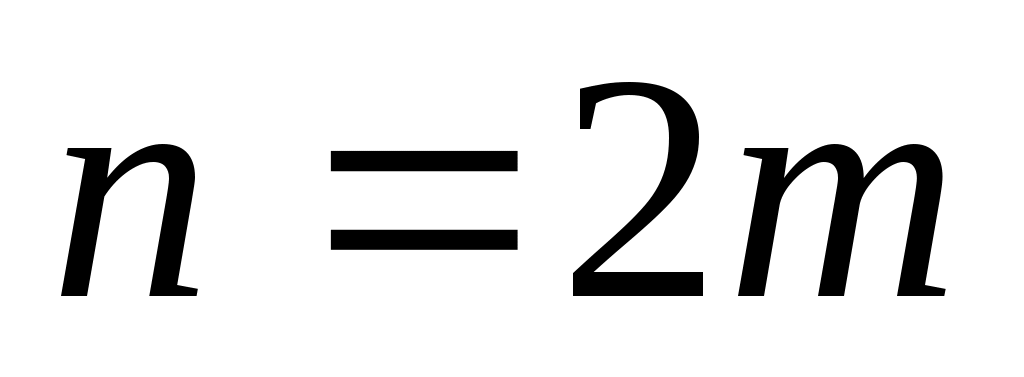 число отрезков длины число отрезков длины 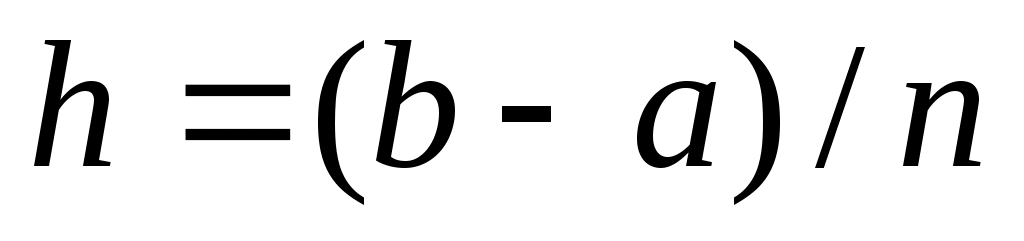 и на каждом из отрезков длины и на каждом из отрезков длины 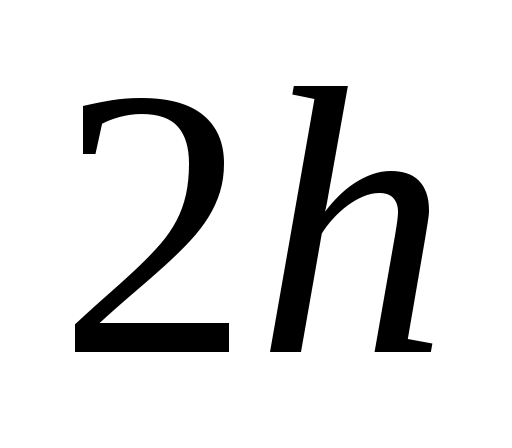 применяют соответствующую формулу. Таким образом получают составные формулы прямоугольников, трапеций и Симпсона. применяют соответствующую формулу. Таким образом получают составные формулы прямоугольников, трапеций и Симпсона.
На сетке 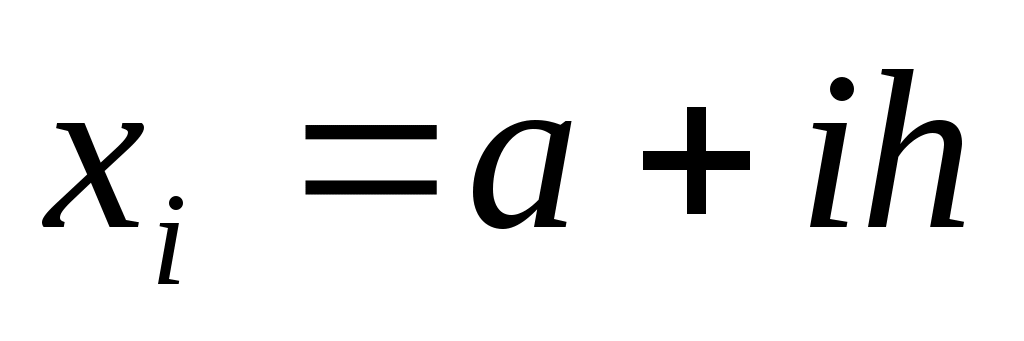 , , 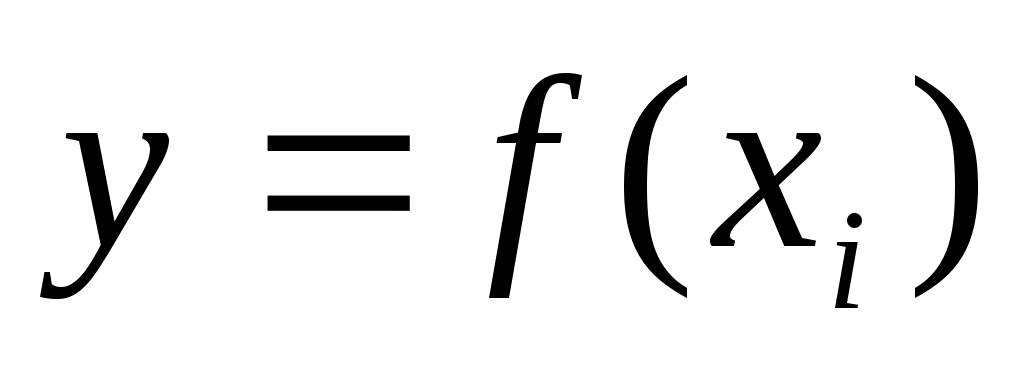 , , 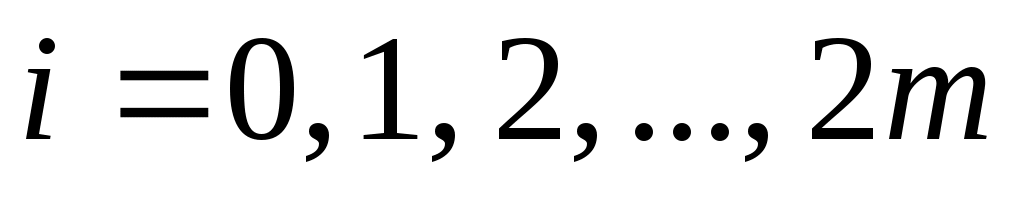 , составные квадратные формулы имеют следующий вид: , составные квадратные формулы имеют следующий вид:
формула прямоугольников
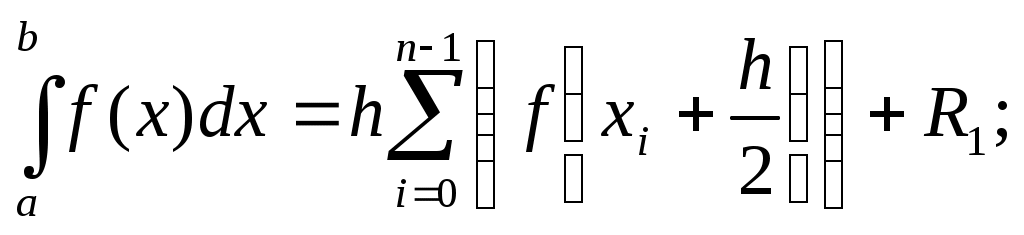
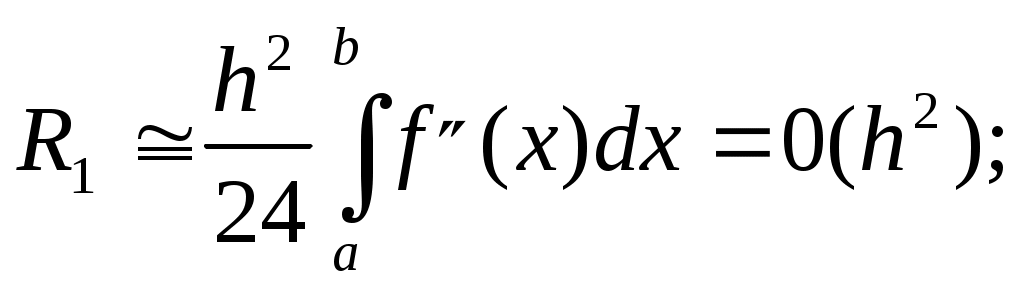
формула трапеций
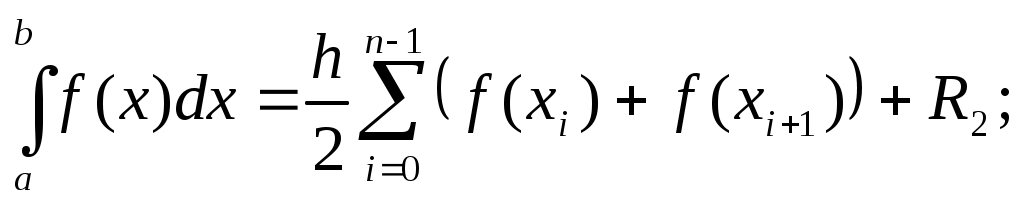
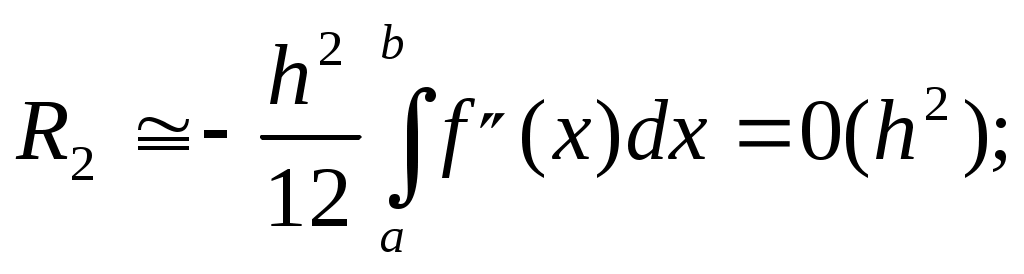
формула Симпсона
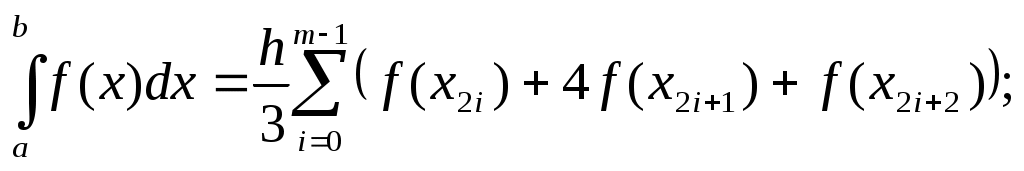
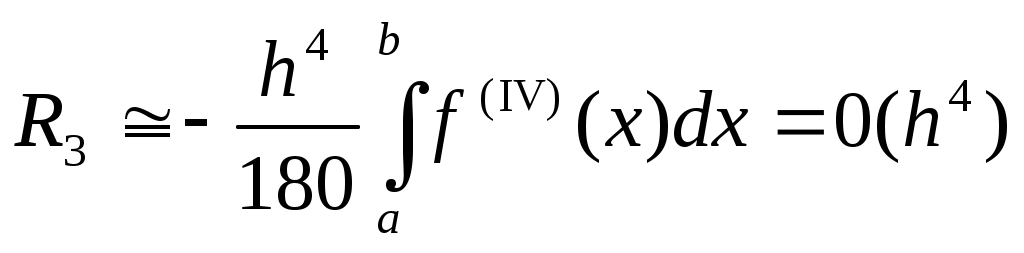 , ,
где 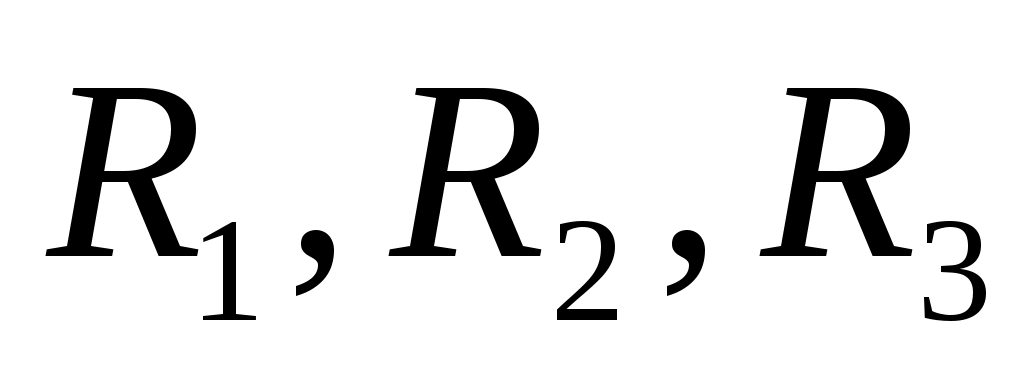 – остаточные члены*). Оценки остаточных членов получены в предположении, что соответствующие производные – остаточные члены*). Оценки остаточных членов получены в предположении, что соответствующие производные 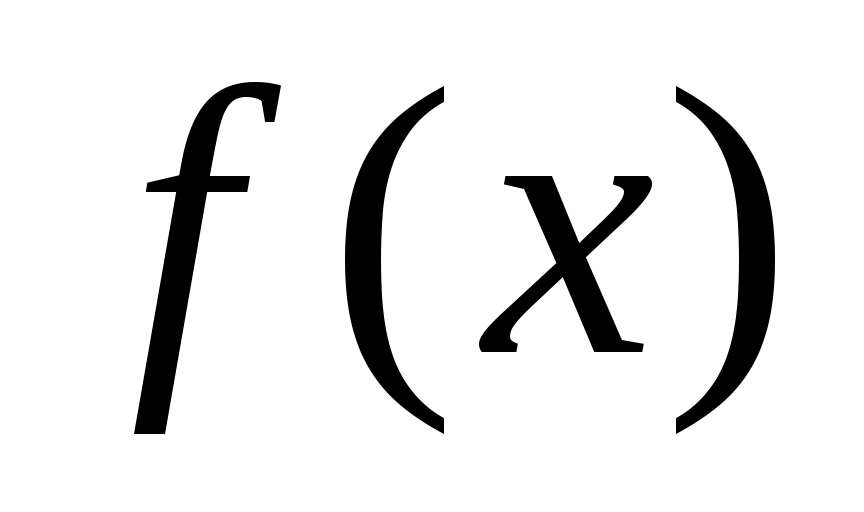 непрерывны на непрерывны на 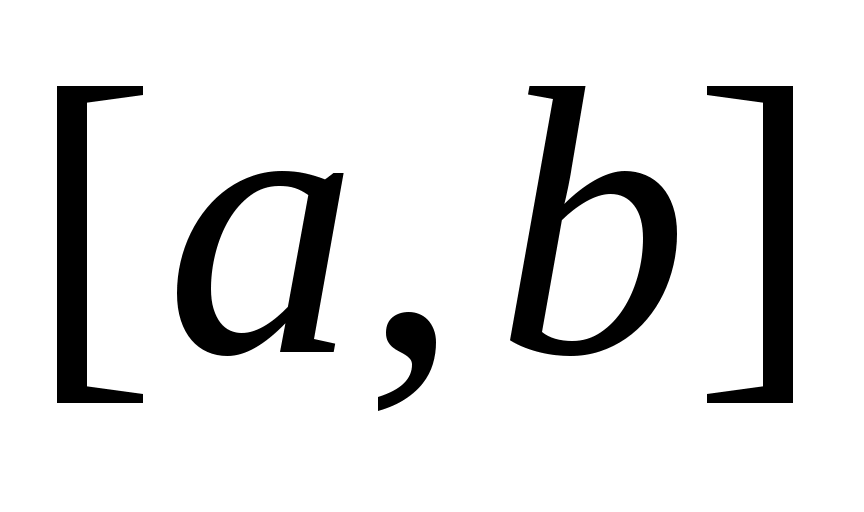 . Нетрудно показать, что при . Нетрудно показать, что при  приближенные значения интегралов для всех трех формул (в предположении отсутствия погрешностей округления**)) стремятся к точному значению интеграла. приближенные значения интегралов для всех трех формул (в предположении отсутствия погрешностей округления**)) стремятся к точному значению интеграла.
Любая попытка сравнить достоинства приведенных формул связана с вопросом типа «что больше 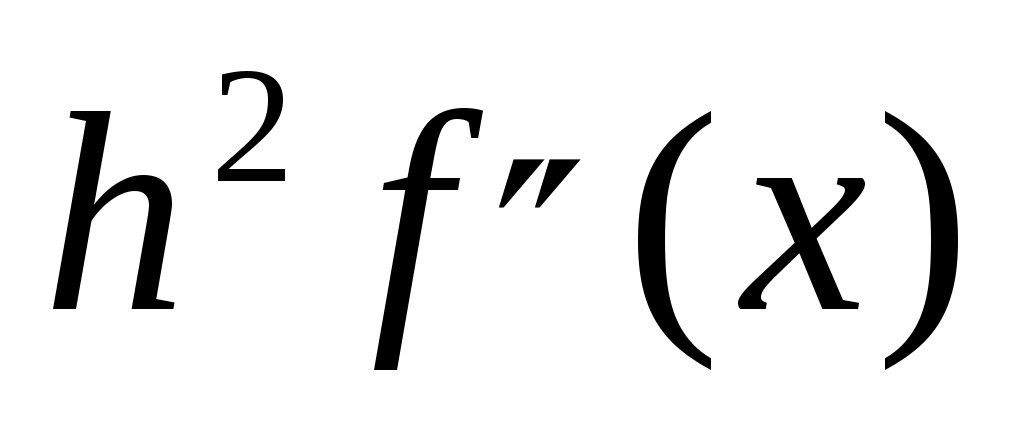 или или 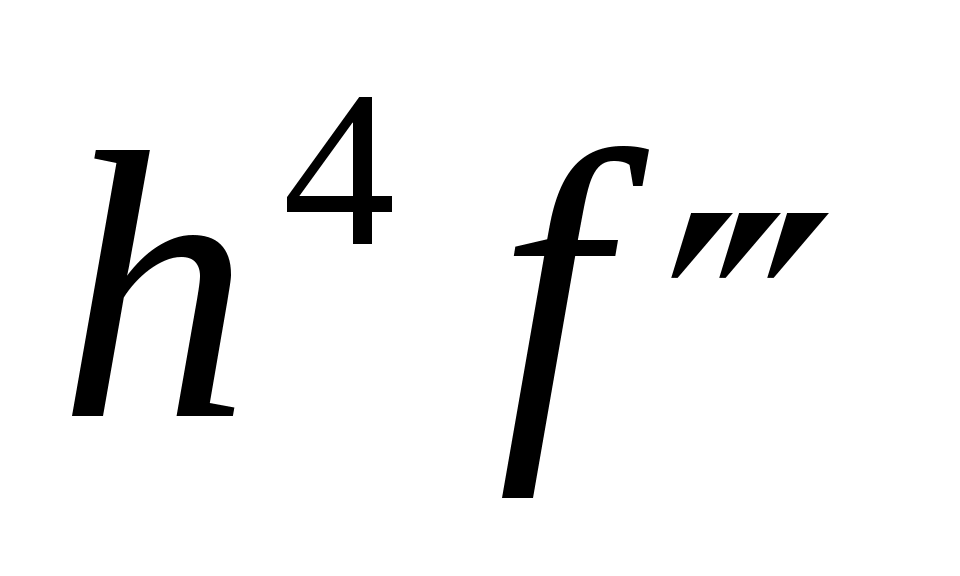 ?» Ответ зависит от свойств интегрируемой функции. Можно лишь утверждать, что остаточный член формулы прямоугольников примерно вдвое меньше, чем формулы трапеций, и оба они имеют порядок ?» Ответ зависит от свойств интегрируемой функции. Можно лишь утверждать, что остаточный член формулы прямоугольников примерно вдвое меньше, чем формулы трапеций, и оба они имеют порядок 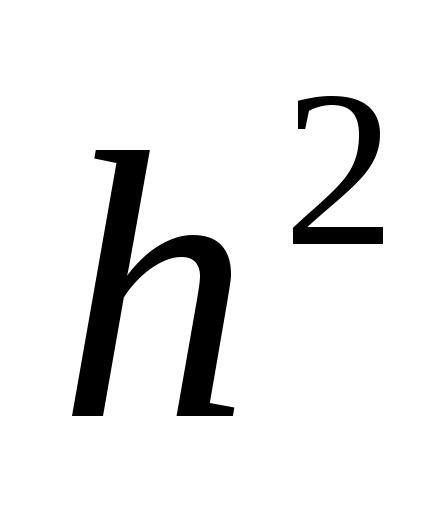 . А остаточный член формулы Симпсона убывает быстрее – со скоростью . А остаточный член формулы Симпсона убывает быстрее – со скоростью 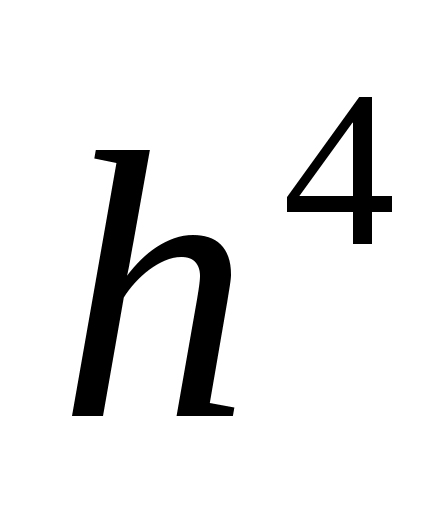 . .
Для практической оценки погрешности квадратурной формулы можно использовать правило Рунге. Для этого проводят вычисления на сетках с шагом 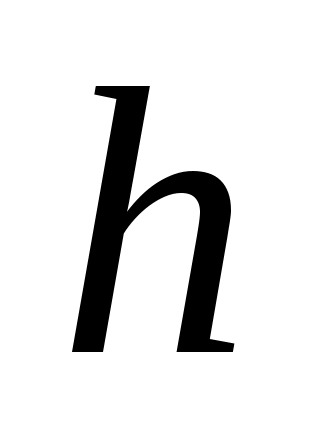 и и 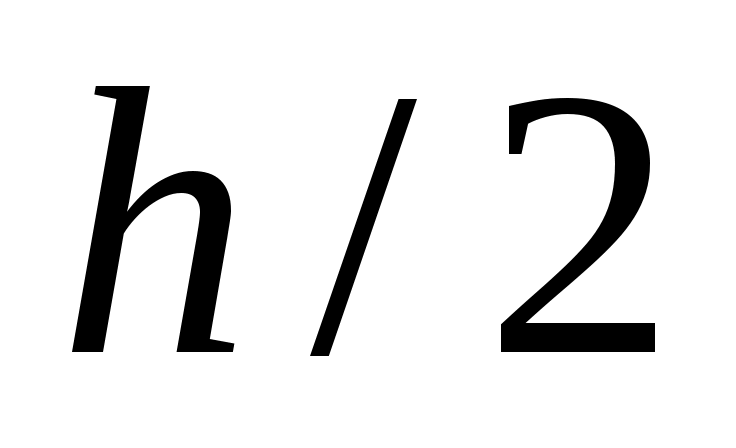 , получают приближенные значения интеграла , получают приближенные значения интеграла 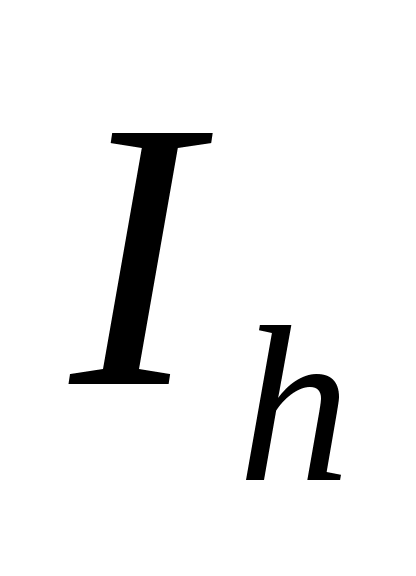 и и 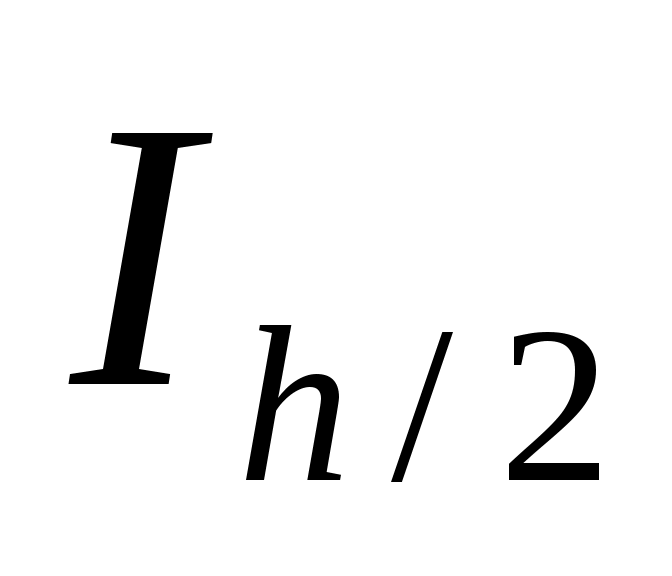 , и за окончательные значения интеграла принимают величины: , и за окончательные значения интеграла принимают величины:
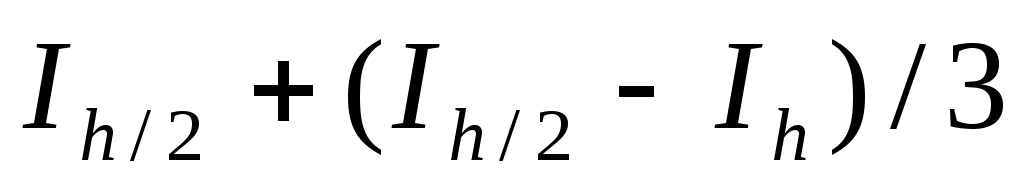 – для формулы прямоугольников; – для формулы прямоугольников;
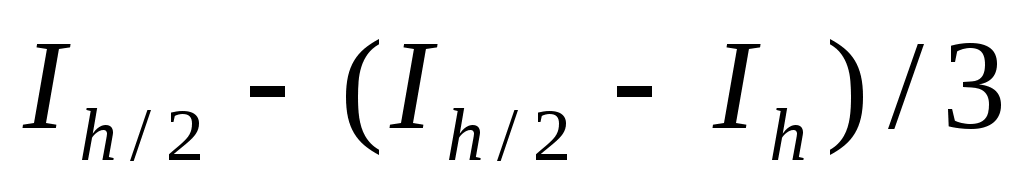 – для формулы трапеций; – для формулы трапеций;
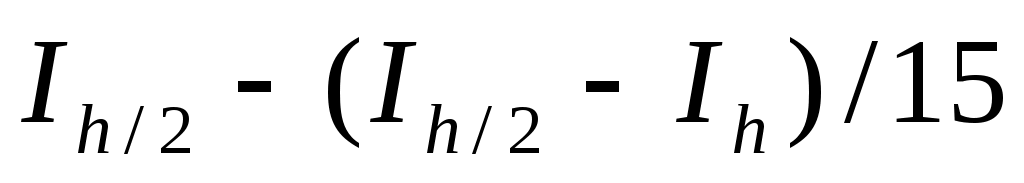 – для формулы Симпсона. – для формулы Симпсона.
При этом за погрешность приближенного значения интеграла принимаем величину
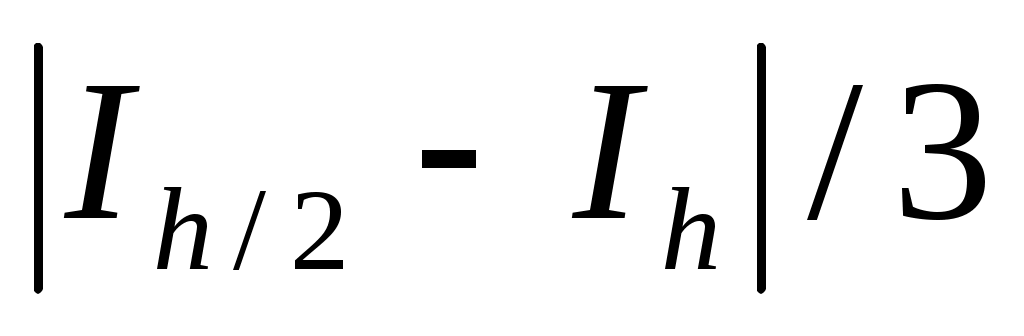 – для формул прямоугольников и трапеций – для формул прямоугольников и трапеций
и величину
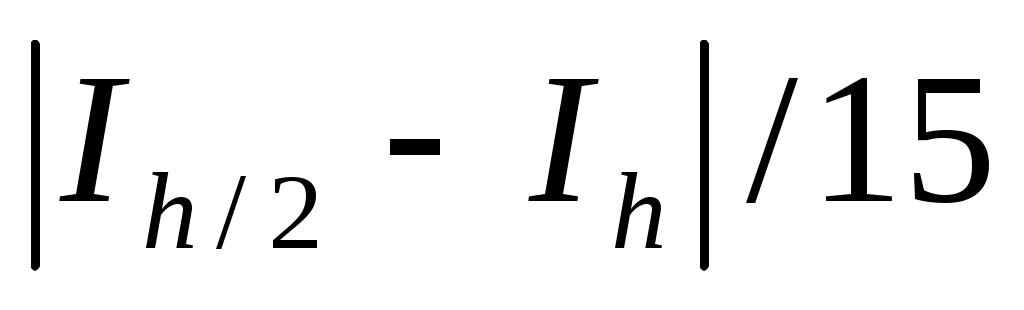 – для формулы Симпсона. – для формулы Симпсона.
Такую оценку погрешностей применяют обычно для построения адаптивных алгоритмов, т.е. таких алгоритмов, которые автоматически так определяют величину шага 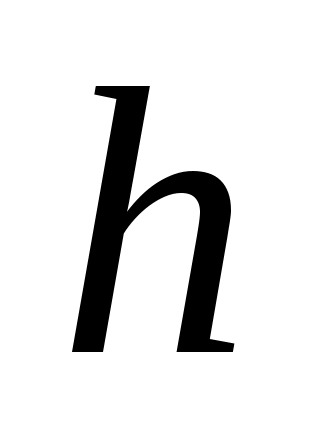 , что результат удовлетворяет требуемой точности. , что результат удовлетворяет требуемой точности.
В настоящей лабораторной работе предлагается с помощью правила Рунге найти по заданной погрешности 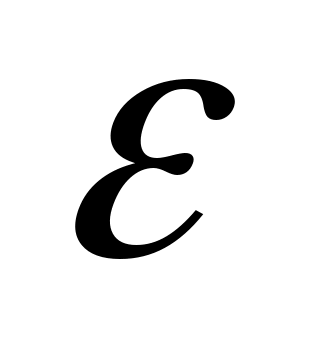 наибольшее значение шага наибольшее значение шага 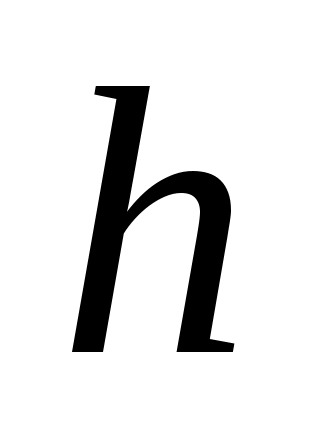 для каждой приведенной квадратурной формулы (наименьшее значение для каждой приведенной квадратурной формулы (наименьшее значение 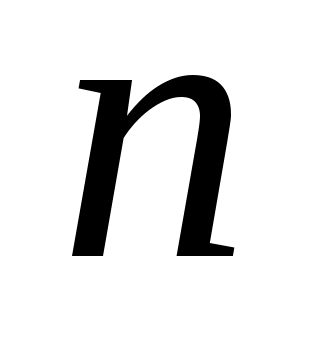 ). ).
Лабораторная работа №5 Приближенное решение задачи Коши методом Рунге-Кутта
Пусть требуется найти решение дифференциального уравнения 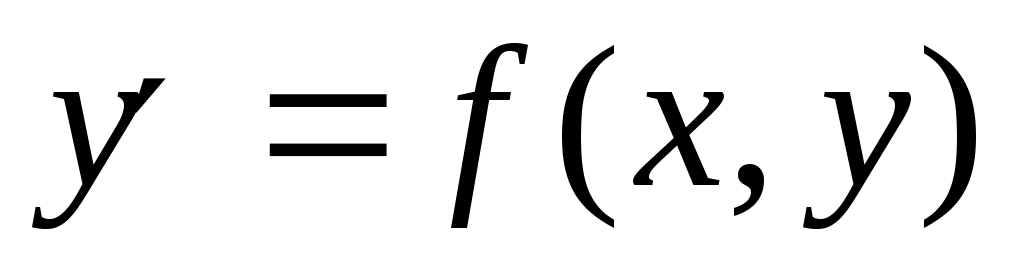 , удовлетворяющее начальному условию , удовлетворяющее начальному условию 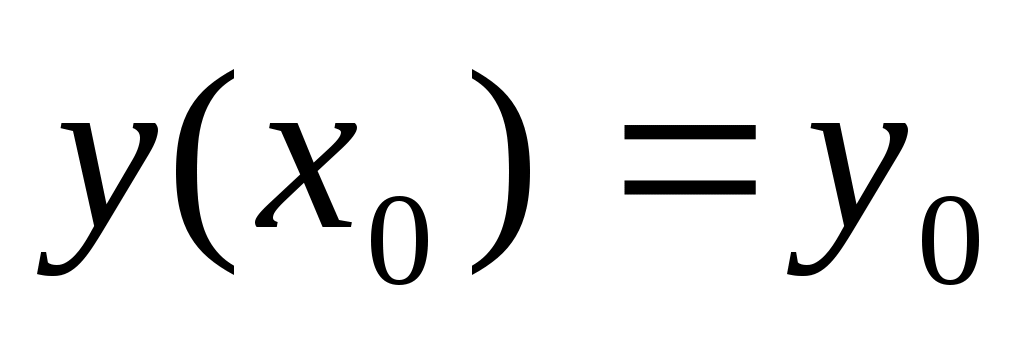 . .
Численное решение задачи состоит в построении таблицы приближенных значений 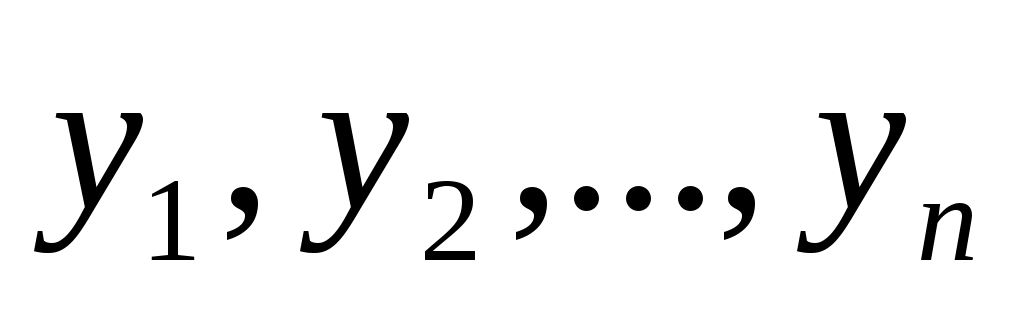 решения уравнения в точках решения уравнения в точках 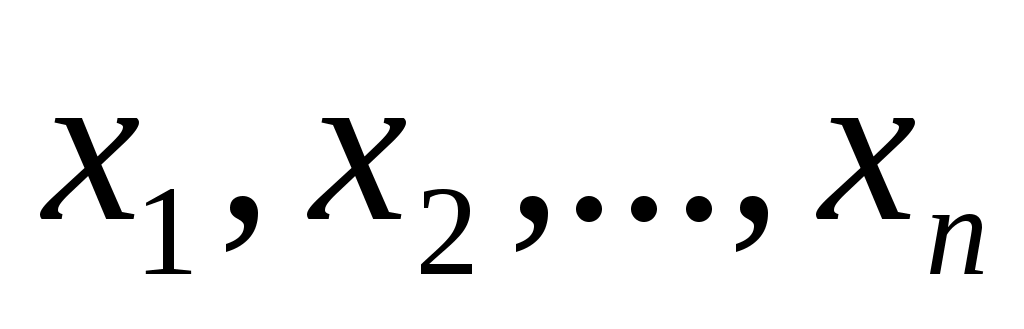 . Точки . Точки 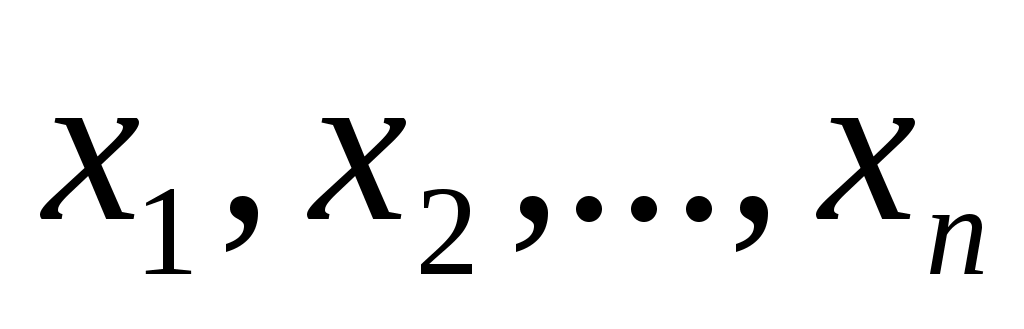 – узлы сетки. Используем систему равноотстоящих узлов. Величина – узлы сетки. Используем систему равноотстоящих узлов. Величина 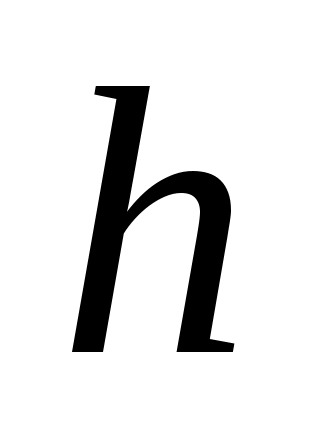 – шаг сетки – шаг сетки 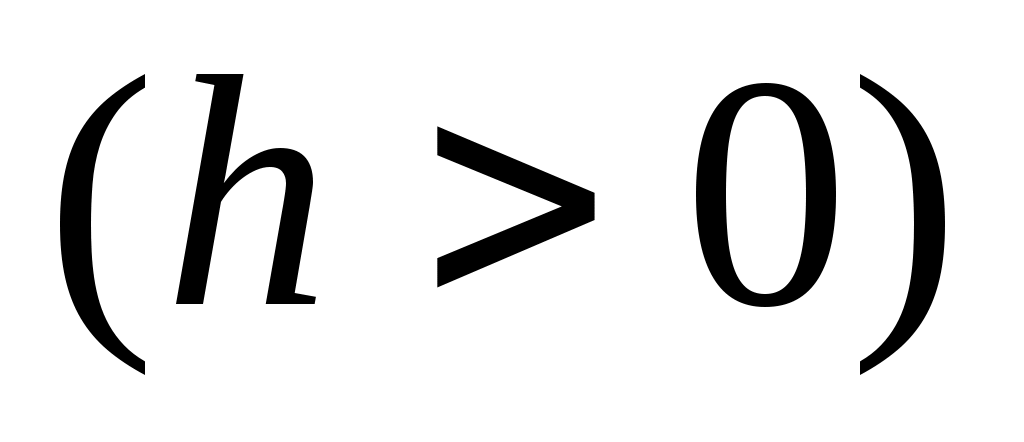 . Методом Рунге- Кутта в литературе обычно называют одношаговый метод четвертого порядка, относящийся к широкому классу методов типа Рунге-Кутта. В этом методе величины . Методом Рунге- Кутта в литературе обычно называют одношаговый метод четвертого порядка, относящийся к широкому классу методов типа Рунге-Кутта. В этом методе величины 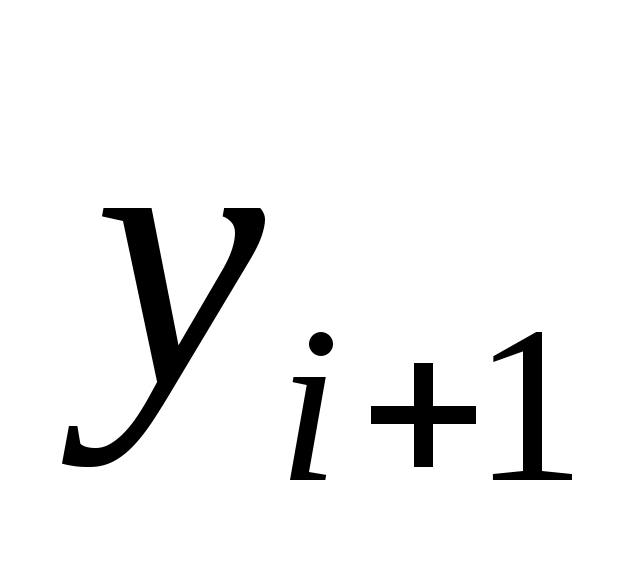 вычисляют по следующим формулам: вычисляют по следующим формулам:
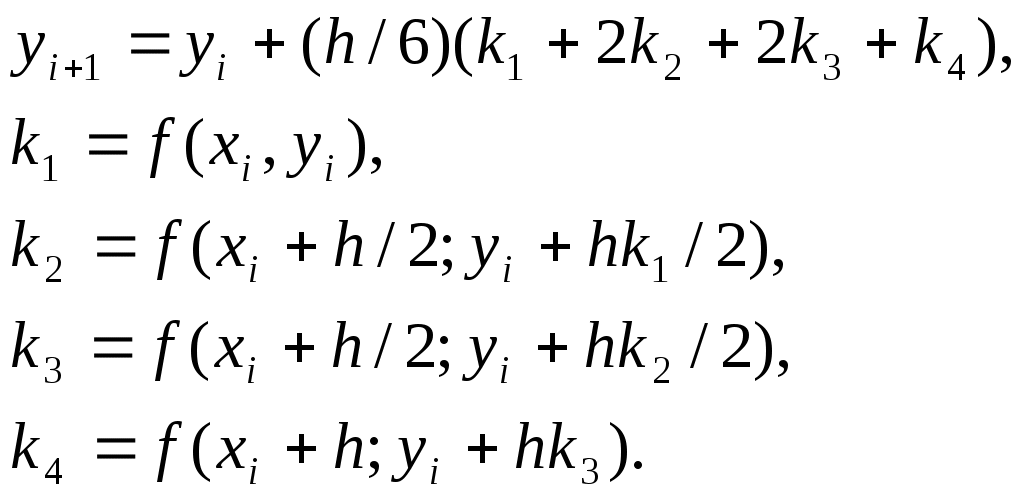 (1) (1)
Погрешность метода на одном шаге сетки равна 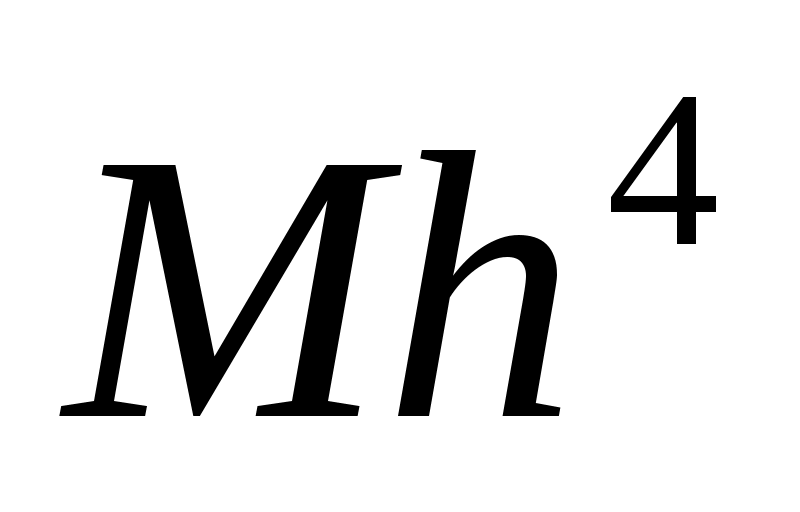 , но на практике оценить величину , но на практике оценить величину 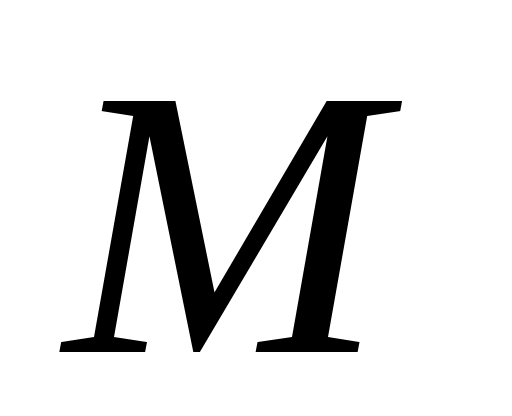 обычно трудно. При оценке погрешности используют правило Рунге. Для этого проводят вычисления сначала с шагом обычно трудно. При оценке погрешности используют правило Рунге. Для этого проводят вычисления сначала с шагом 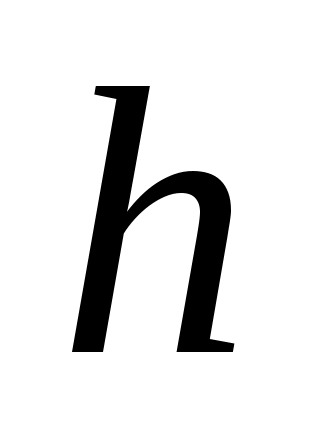 , а затем – с шагом , а затем – с шагом 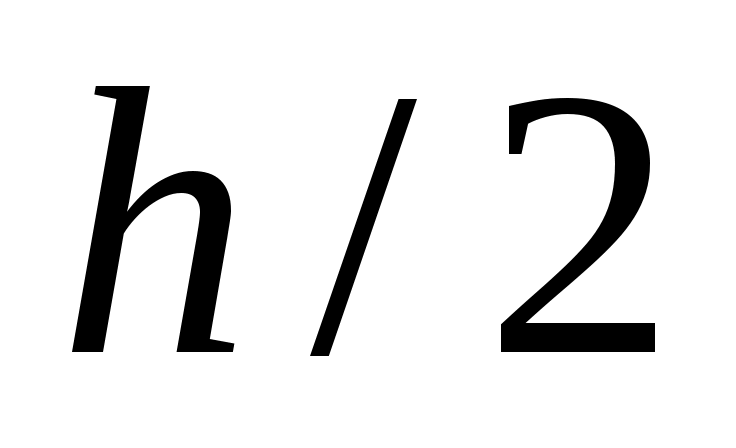 . Если . Если 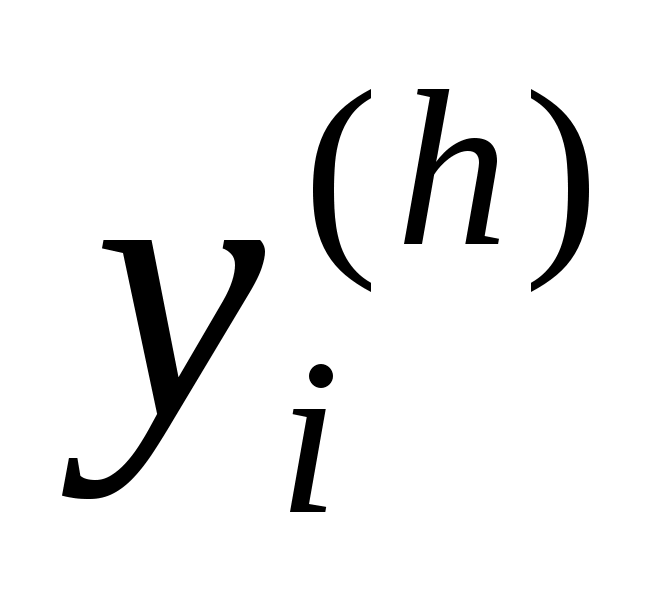 – приближение, вычисленное с шагом – приближение, вычисленное с шагом 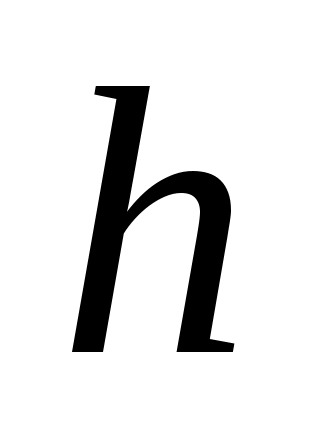 , а , а 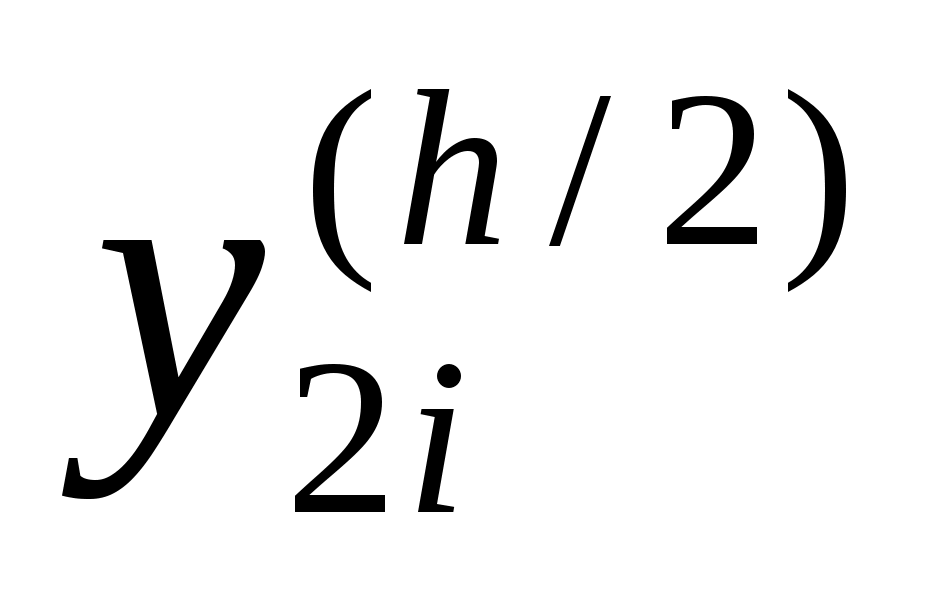 – с шагом – с шагом 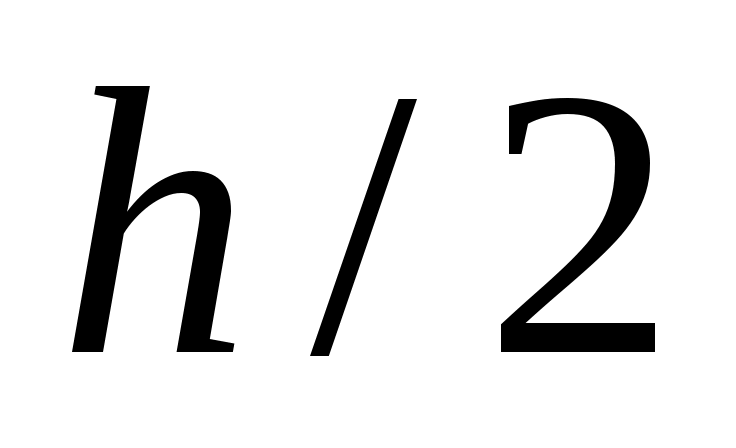 , то справедлива оценка , то справедлива оценка
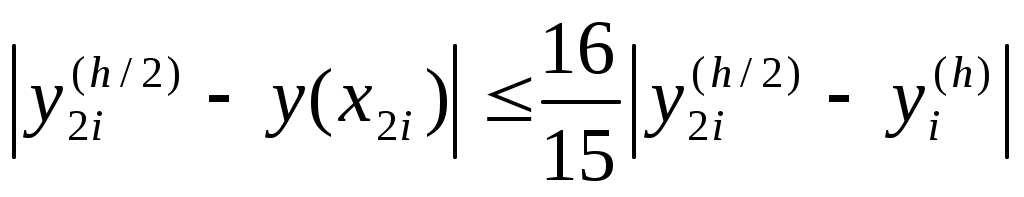 . .
За оценку погрешности вычислений с шагом 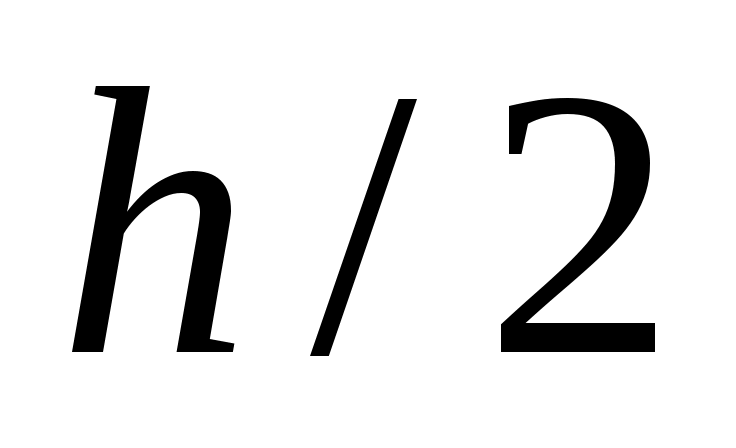 можно принять величину можно принять величину
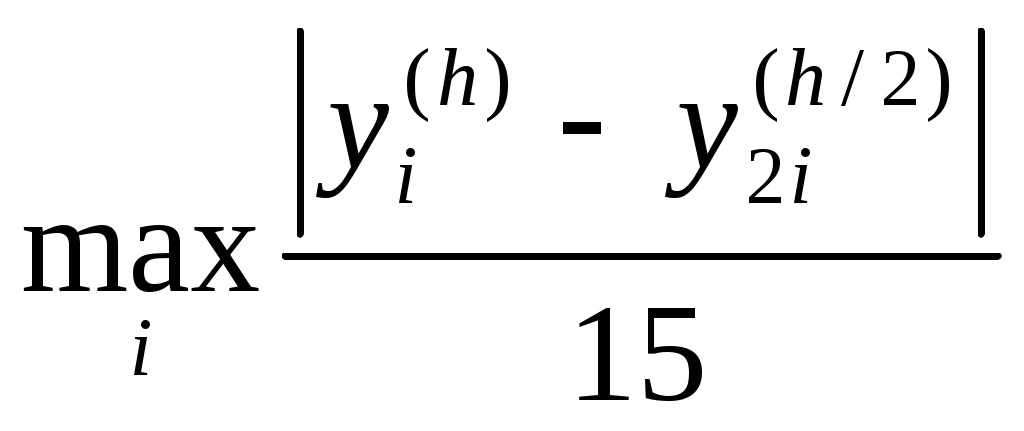 . .
Метод Рунге-Кутта легко переносится на нормальные системы дифференциальных уравнений вида
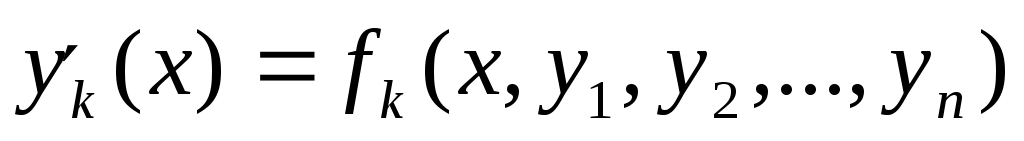 , , 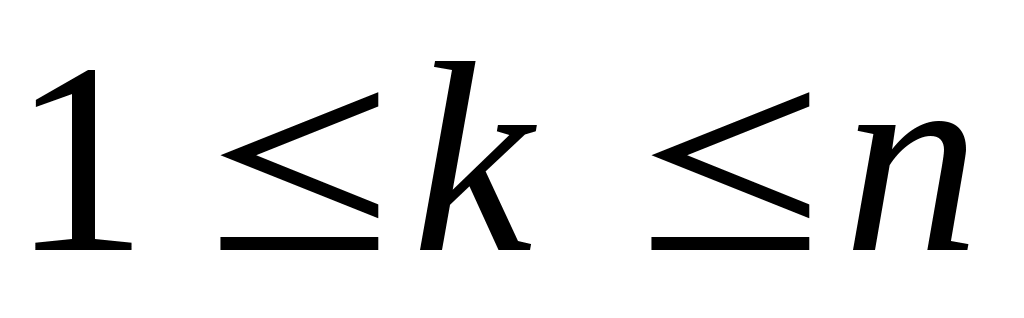 , ,
которые для краткости удобно записывать в векторной форме:
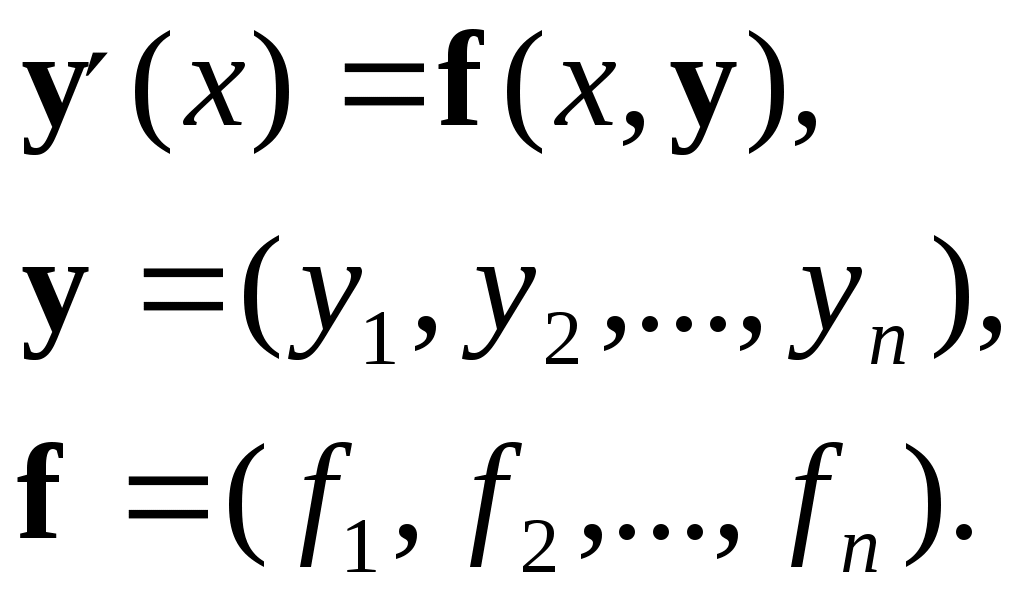
Для получения расчетных формул методом Рунге-Кутта достаточно в формулах (1) заменить 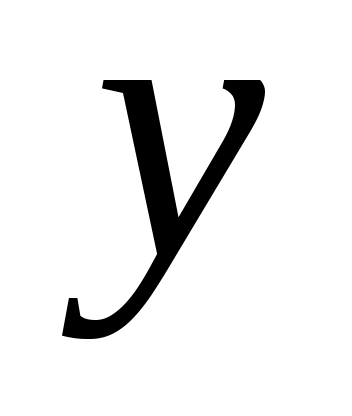 и и 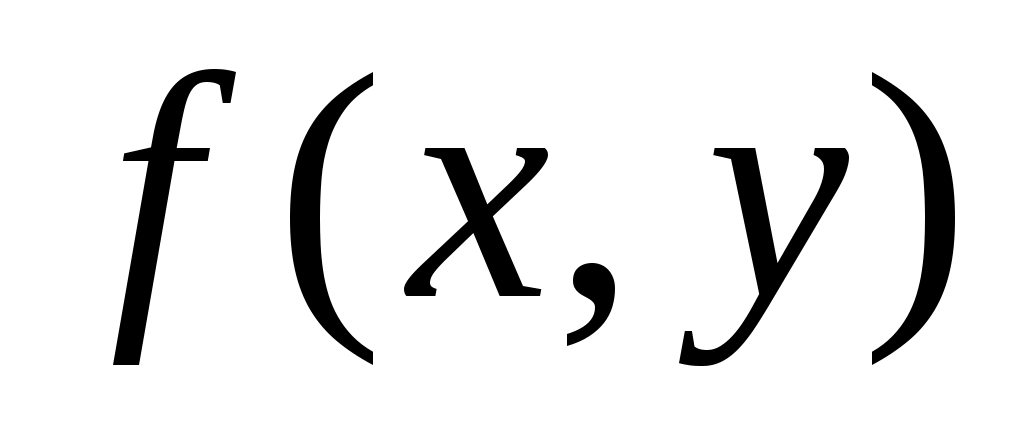 соответственно на соответственно на  и и 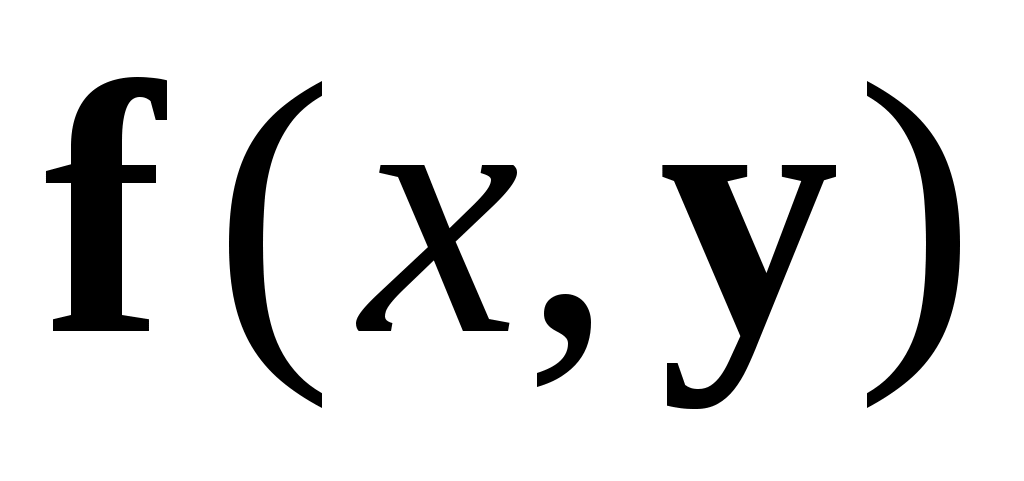 , а коэффициенты , а коэффициенты 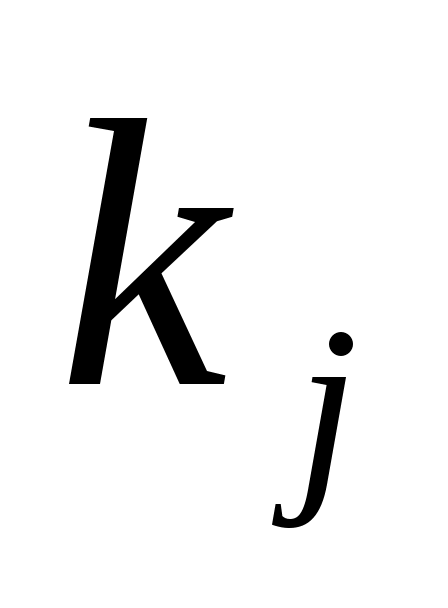 – на – на 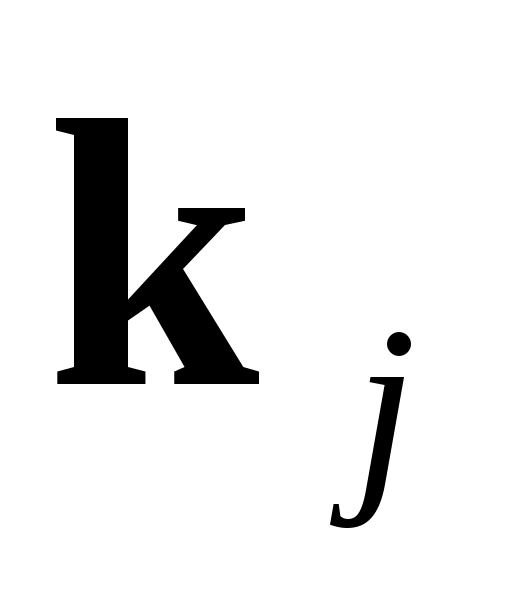  . .
Лабораторная работа №6
Аппроксимация функции с помощью кубического сплайна
Типичной задачей приближения функций является задача интерполяции: по заданной таблице чисел 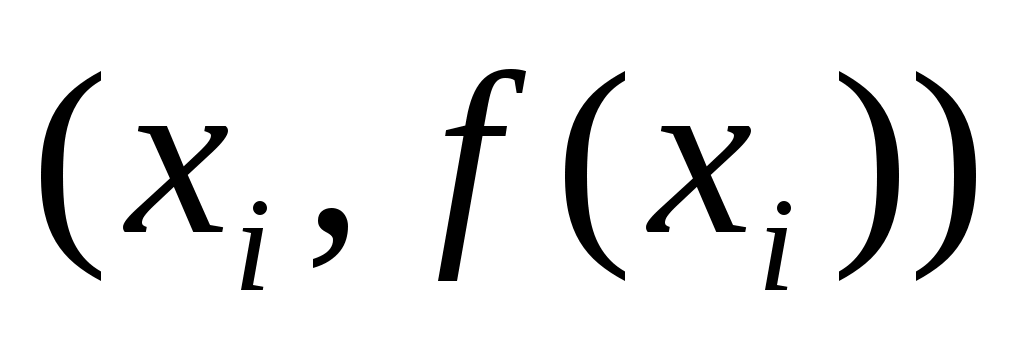 , , 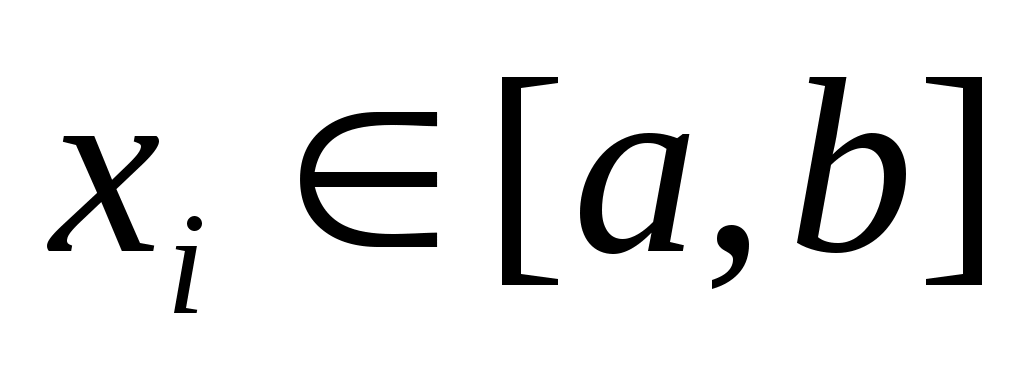 , , 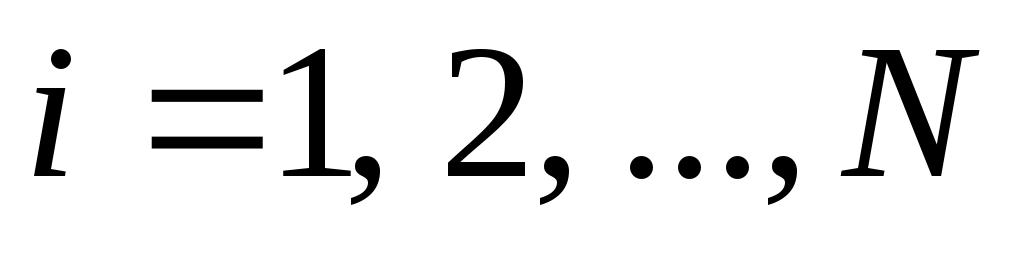 , вычислить функцию , вычислить функцию 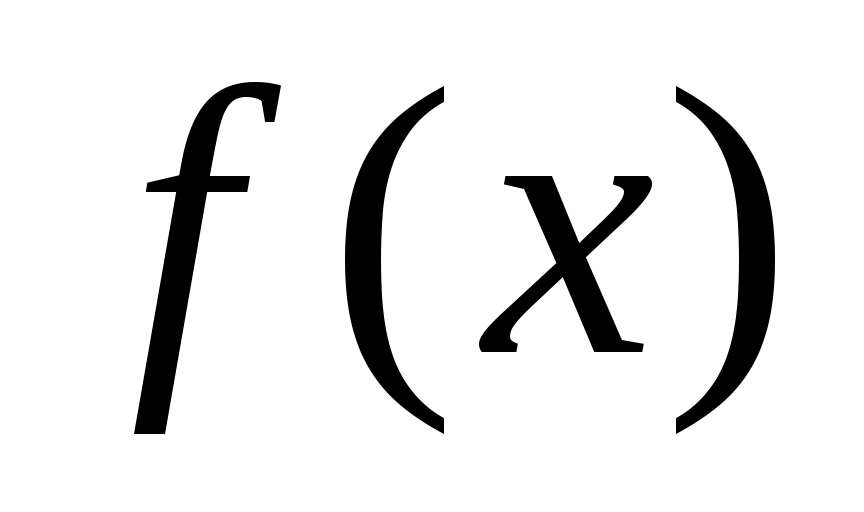 с той или иной точностью на отрезке с той или иной точностью на отрезке 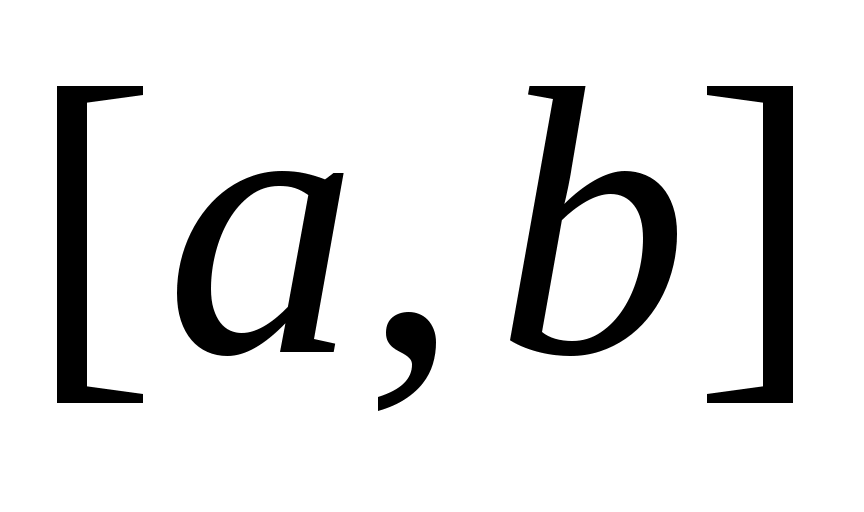 действительной оси. действительной оси.
Классический метод решения этой задачи основан на построении интерполяционного многочлена Лагранжа, определяемого равенством
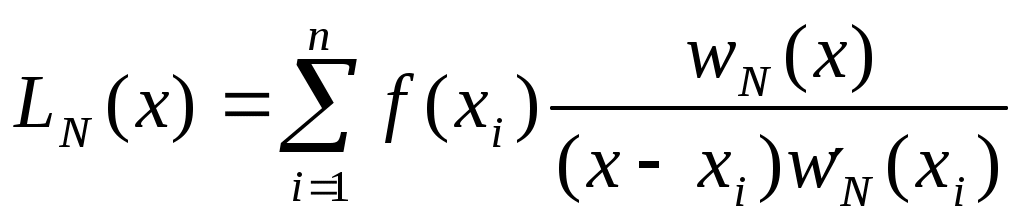 , , 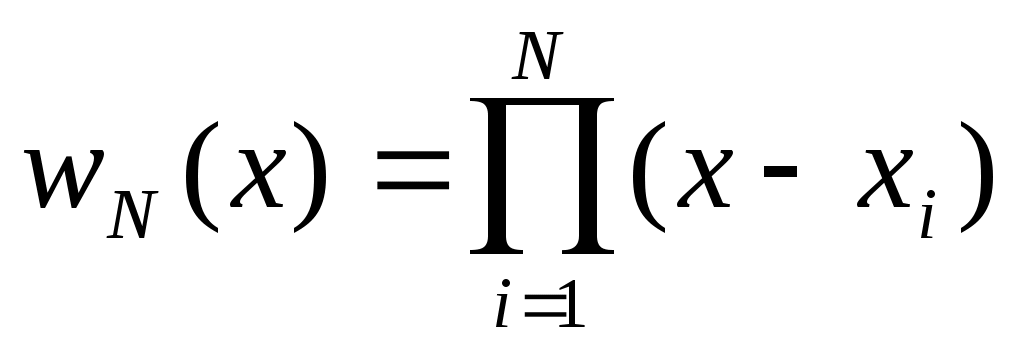 . .
Хотя, согласно теореме Вейерштрасса, всякая непрерывная на отрезке 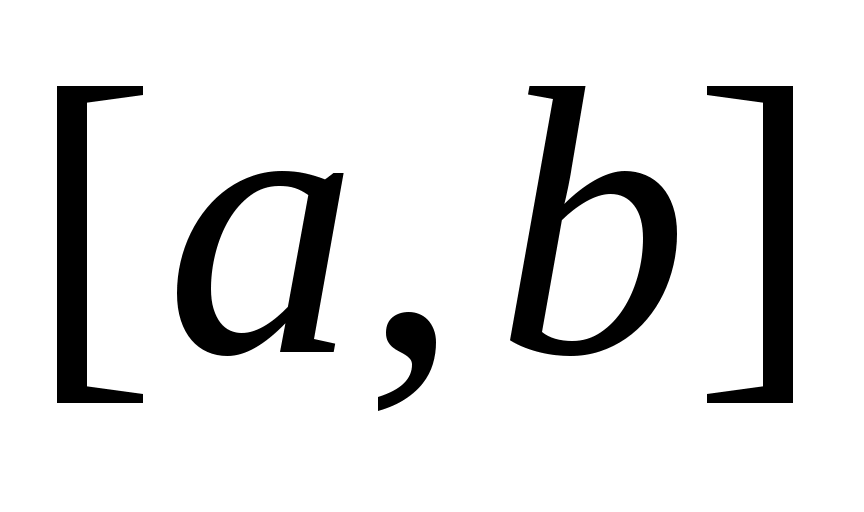 функция функция 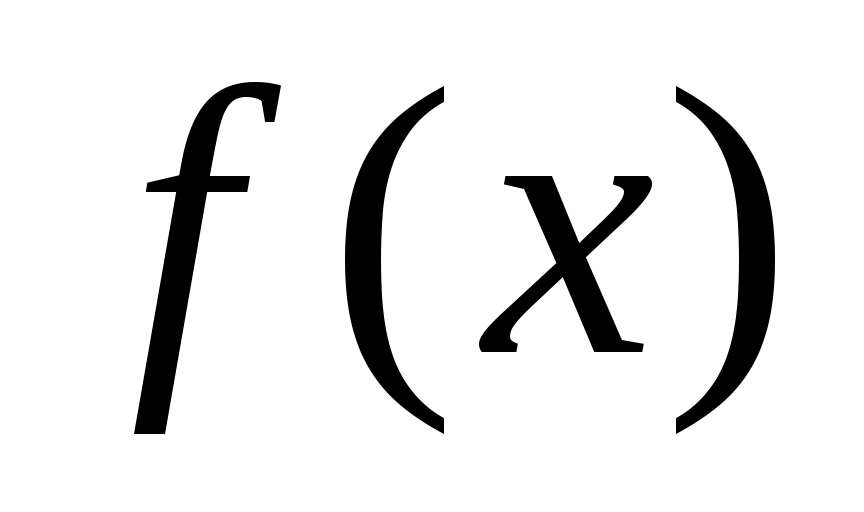 может быть как угодно точно приближена многочленом, практическая возможность применения многочленов ограничена. может быть как угодно точно приближена многочленом, практическая возможность применения многочленов ограничена.
Ряд примеров показывает, что даже при большом числе узлов интерполяционный многочлен Лагранжа не гарантирует хорошее приближение функции. Например, С. Н. Бернштейном было установлено, что последовательность интерполяционных многочленов Лагранжа, построенных для непрерывной на отрезке 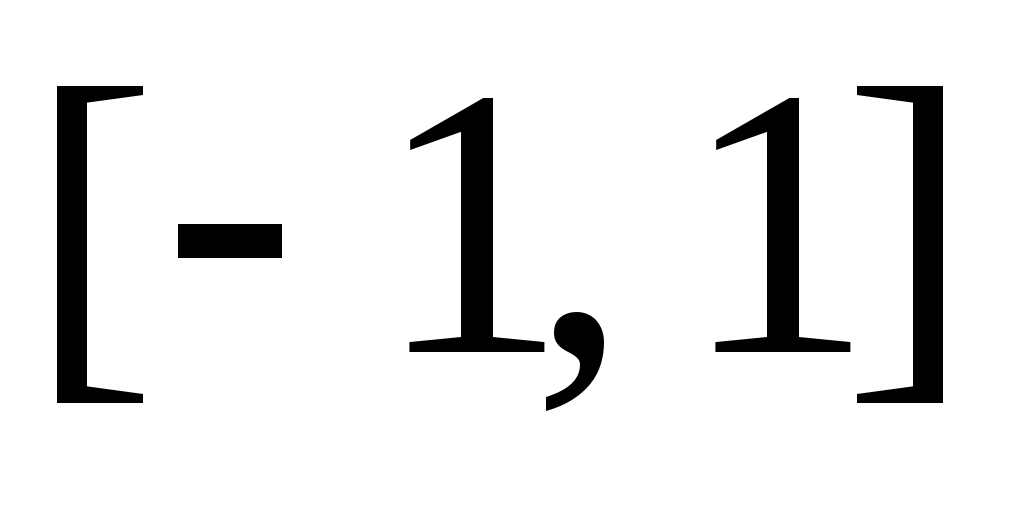 функции функции 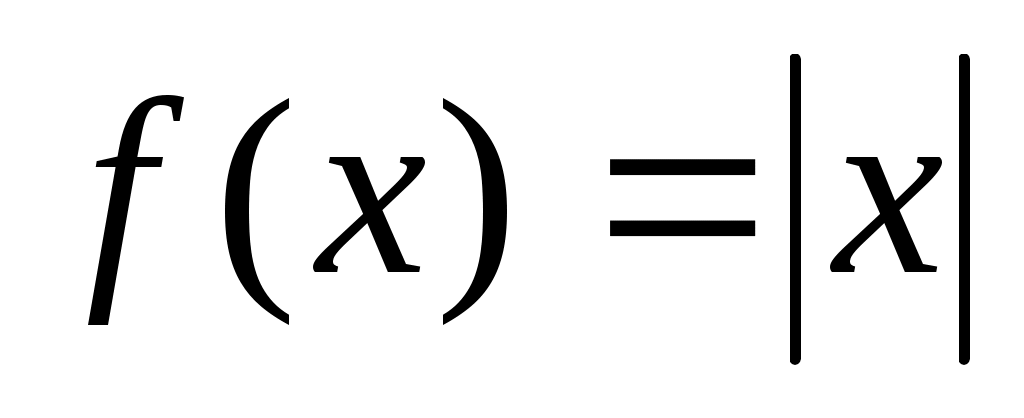 по равноотстоящим узлам, не сходится при возрастании числа узлов по равноотстоящим узлам, не сходится при возрастании числа узлов  к к 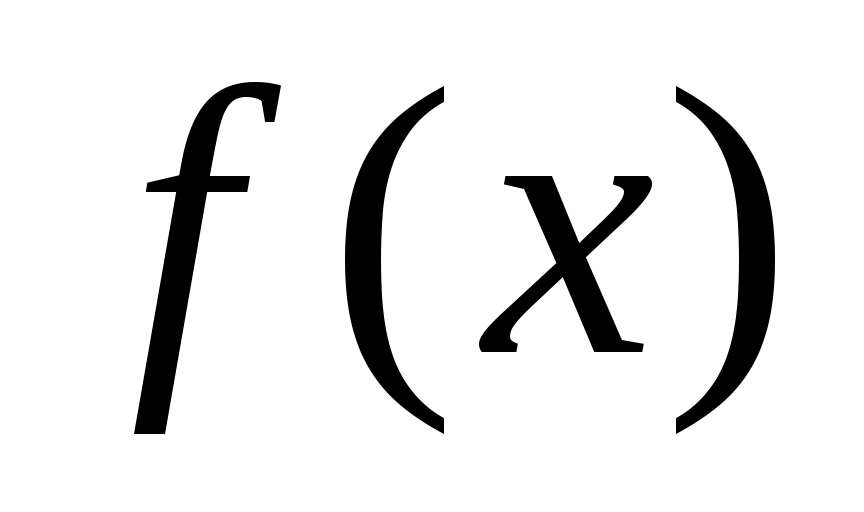 . Еще более замечательный пример построен Рунге, который в качестве тестовой функции взял бесконечно дифференцируемую функцию . Еще более замечательный пример построен Рунге, который в качестве тестовой функции взял бесконечно дифференцируемую функцию
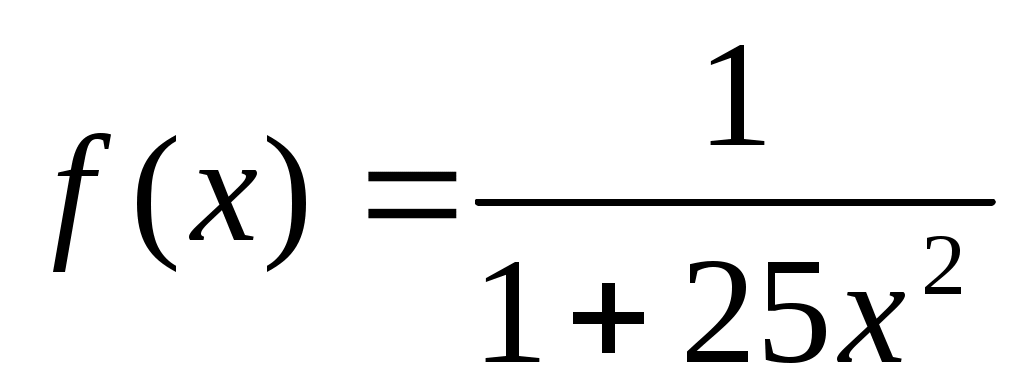 . .
Однако, несмотря на ее гладкость, последовательность интерполяционных многочленов Лагранжа не сходилась к этой функции в равномерной норме. А именно, в обоих случаях было получено, что
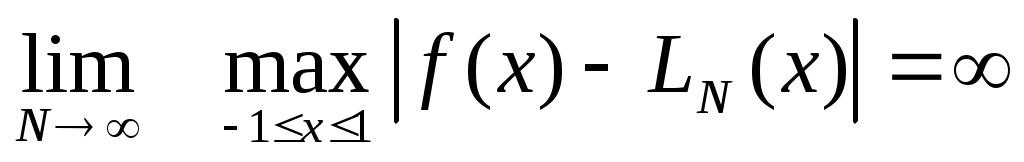 . .
В частности, в примере Рунге установлено, что
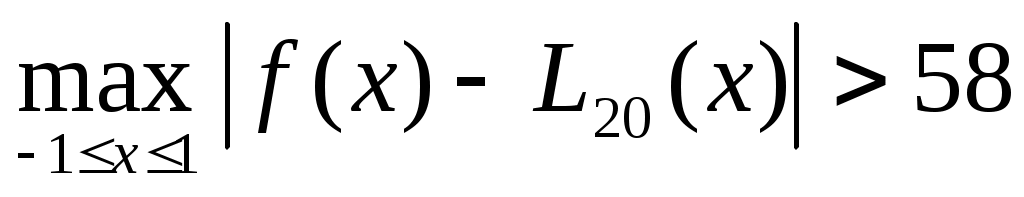 . .
Относительная погрешность такой интерполяции составляет величину около 10 000%.
Иногда трудности построения хороших интерполяционных многочленов удается преодолеть за счет перехода к специальным многочленам или выбора подходящей системы узлов интерполяции.
Однако, на практике, для того, чтобы аппроксимировать функцию, вместо построения глобального интерполяционного многочлена на всем промежутке используют интерполяцию кусочными многочленами.
Простейшим примером такого рода является кусочно-линейная интерполяция. В общем случае отрезок  точками точками 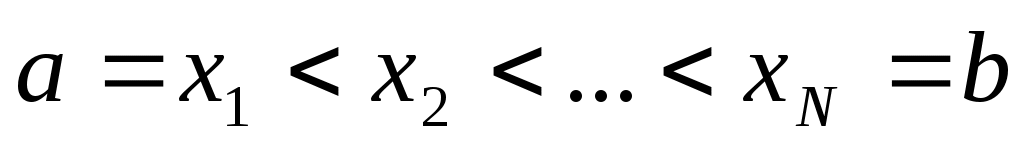 разбивают на части и на каждом промежутке разбивают на части и на каждом промежутке 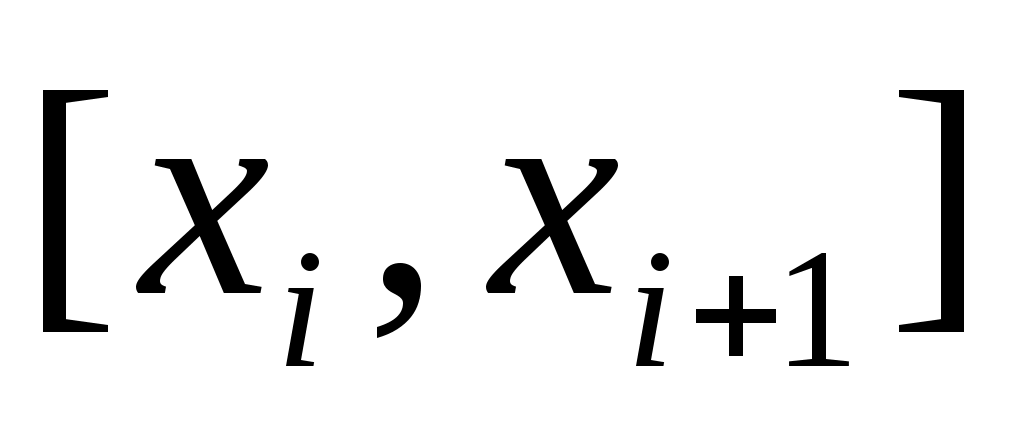 , , 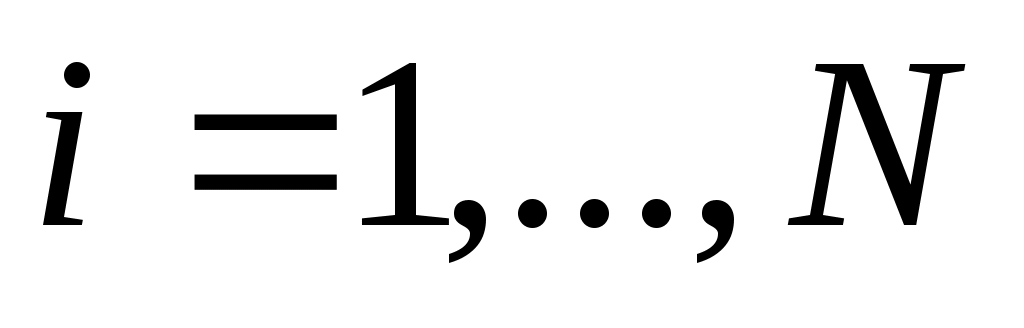 строят свой интерполяционный многочлен. Полученные таким образом многочлены (обычно одной степени) дают интерполяцию функции на всем отрезке. Такой интерполяционный многочлен-многозвенник может обладать различными свойствами, которые определяются степенью используемых многочленов на каждом отрезке строят свой интерполяционный многочлен. Полученные таким образом многочлены (обычно одной степени) дают интерполяцию функции на всем отрезке. Такой интерполяционный многочлен-многозвенник может обладать различными свойствами, которые определяются степенью используемых многочленов на каждом отрезке 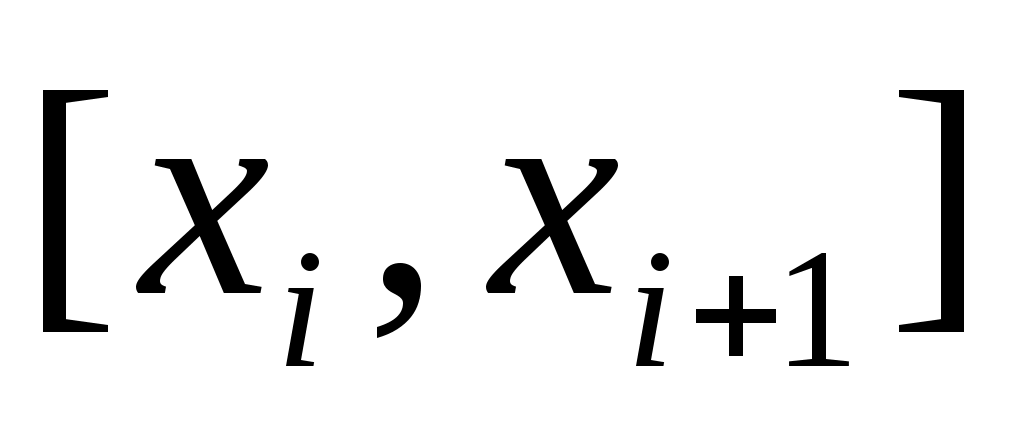 и условиями сопряжения на концах соседних отрезков. Полученные при этом гладкие кусочно-многочленные функции (составленные из многочленов одной и той же степени) называются сплайнами. Сплайн называется кубическим, если он составлен из многочленов третьей степени. и условиями сопряжения на концах соседних отрезков. Полученные при этом гладкие кусочно-многочленные функции (составленные из многочленов одной и той же степени) называются сплайнами. Сплайн называется кубическим, если он составлен из многочленов третьей степени.
Гладкие сплайны обладают многими замечательными свойствами, которые и обеспечили им успех в приложениях. Так, для функции, рассмотренной в примере Рунге, кубический сплайн на сетке с шестью узлами дает погрешность настолько малую, что она не может быть изображена на одном графике с 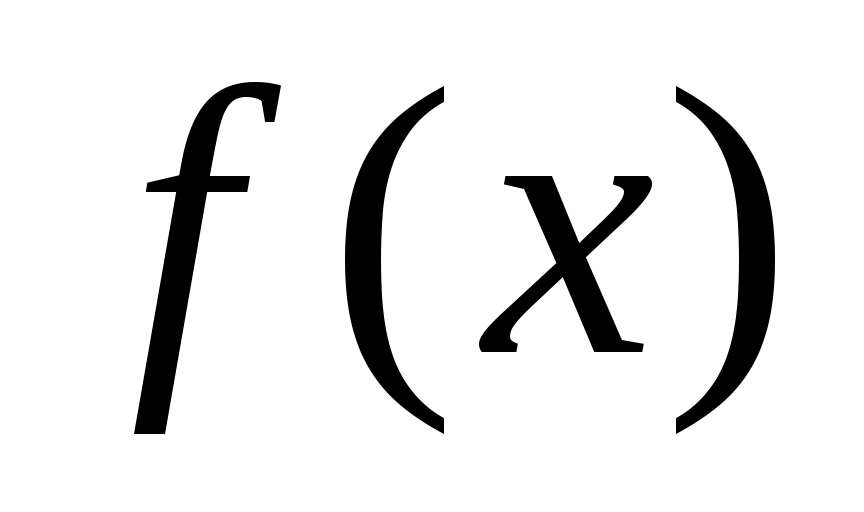 . Алгоритмы построения кубических сплайнов весьма просты и легко реализуются на ЭВМ. . Алгоритмы построения кубических сплайнов весьма просты и легко реализуются на ЭВМ.
Перейдем к построению кубических сплайнов класса 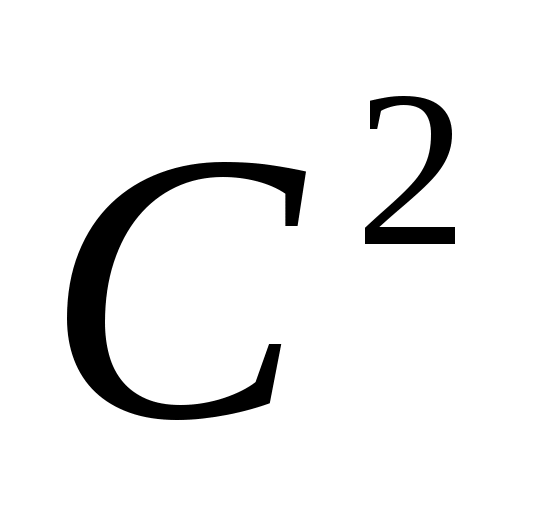 (являющихся дважды непрерывно дифференцируемыми функциями). (являющихся дважды непрерывно дифференцируемыми функциями).
Пусть на отрезке 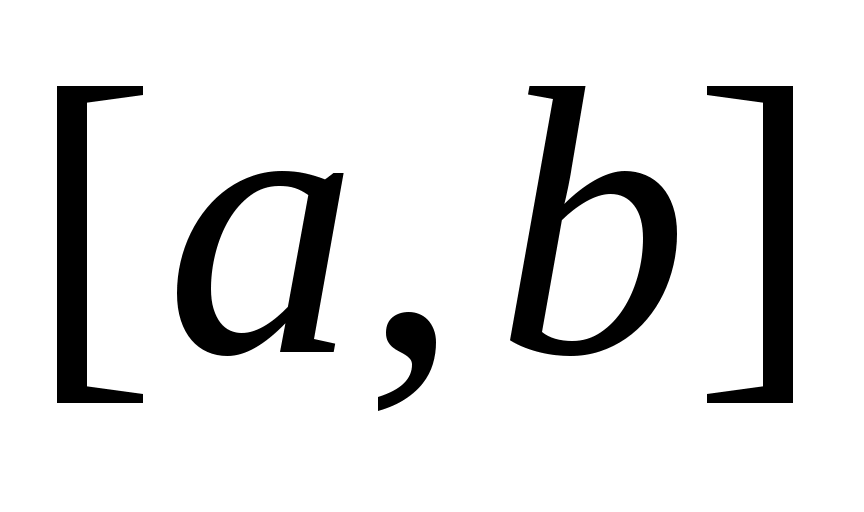 в узлах сетки в узлах сетки 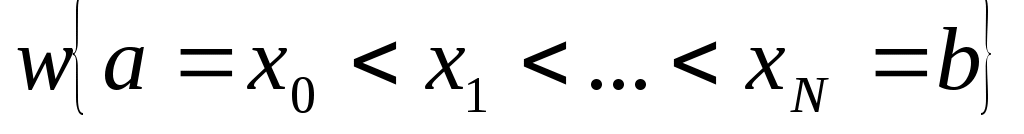 заданы значения некоторой функции заданы значения некоторой функции 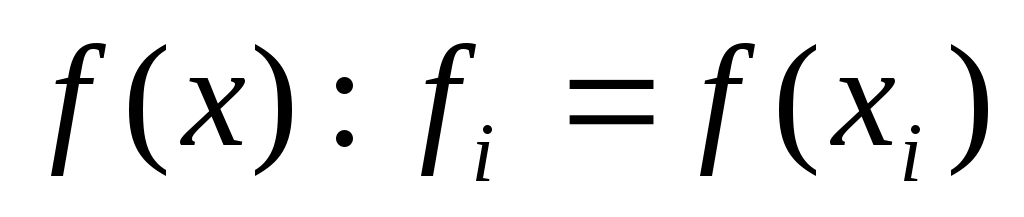 , , 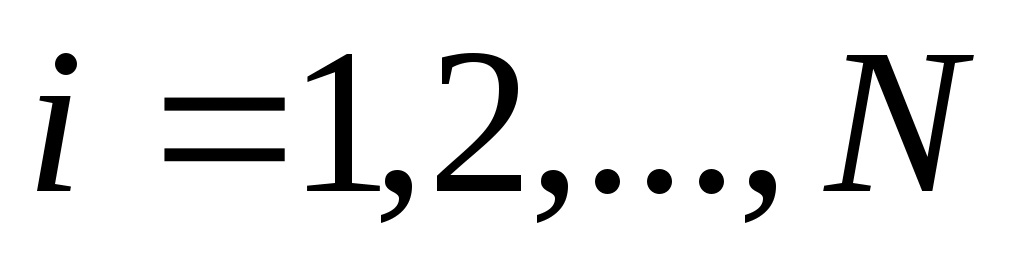 . Интерполяционным кубическим сплайном . Интерполяционным кубическим сплайном 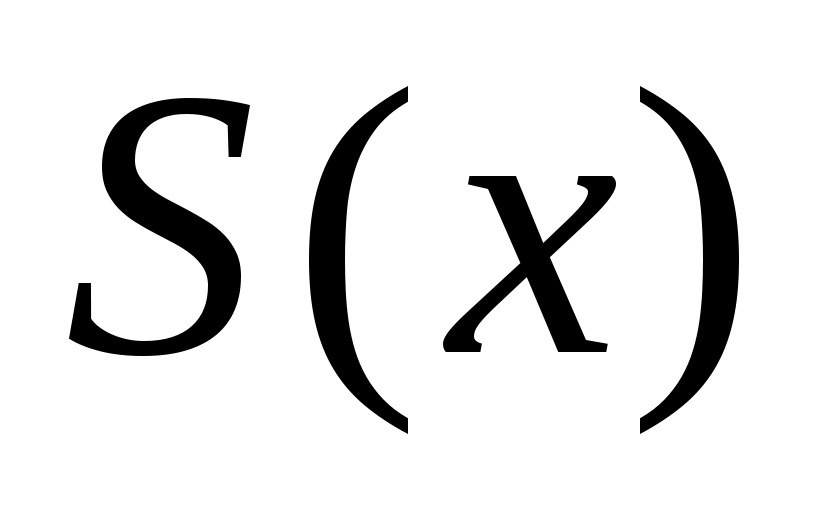 называется сплайн, удовлетворяющий условиям: называется сплайн, удовлетворяющий условиям:
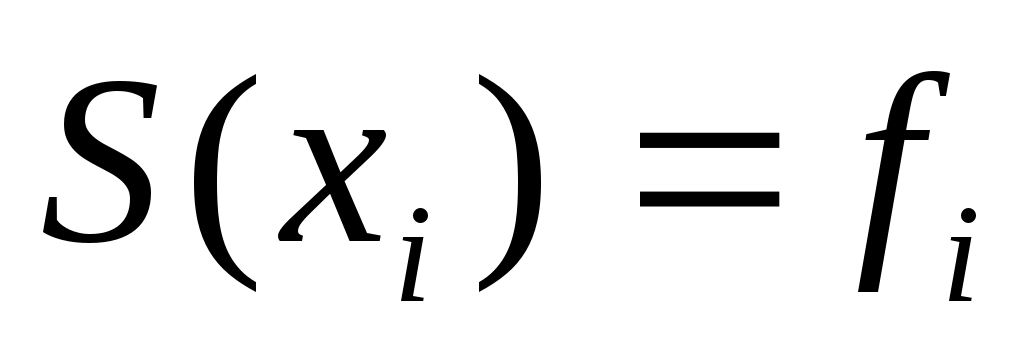 , , 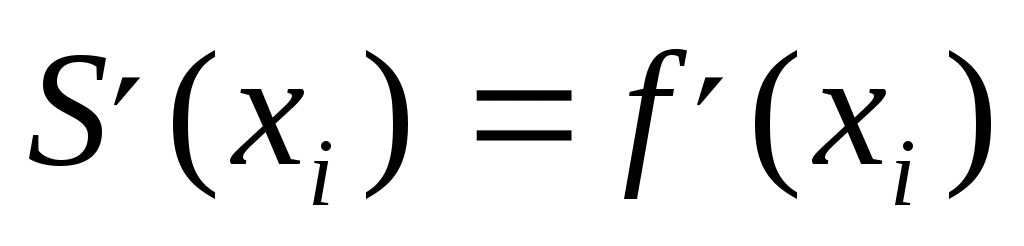 , , 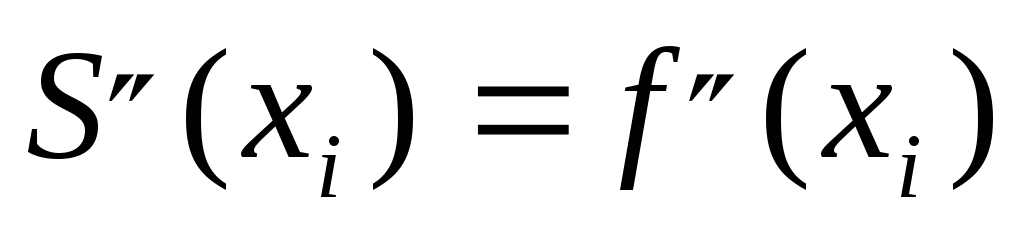 . (1) . (1)
Так как 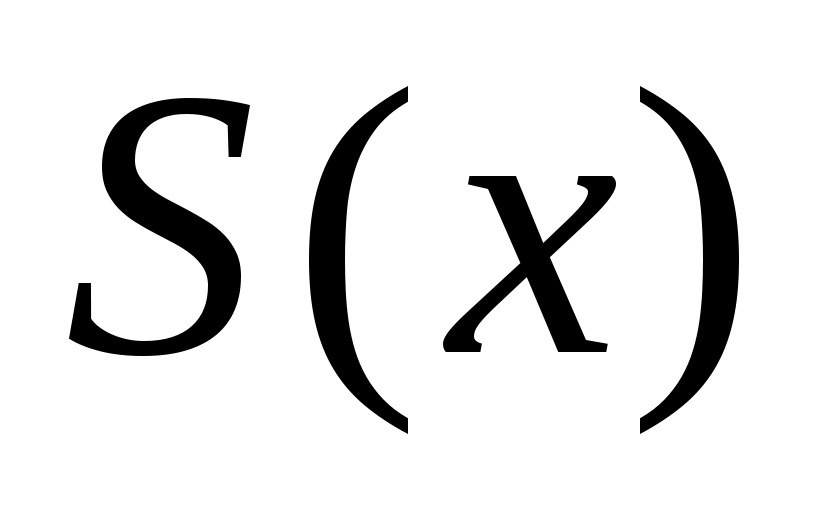 – кубический сплайн, то на каждом из отрезков – кубический сплайн, то на каждом из отрезков 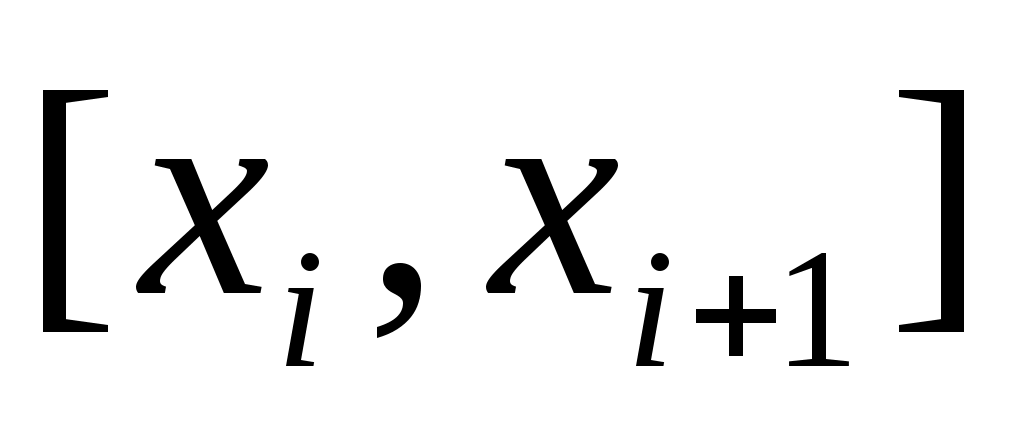 он определяется четырьмя коэффициентами, и поэтому для его построения на всем промежутке он определяется четырьмя коэффициентами, и поэтому для его построения на всем промежутке 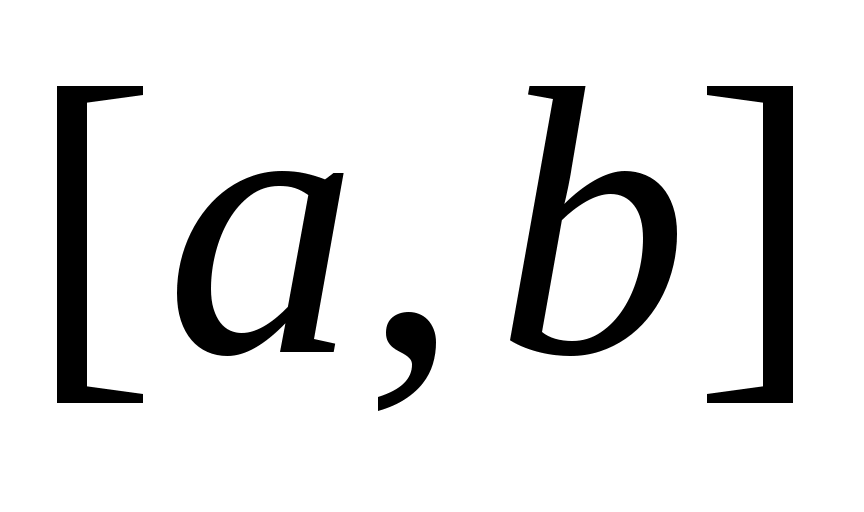 необходимо определить необходимо определить 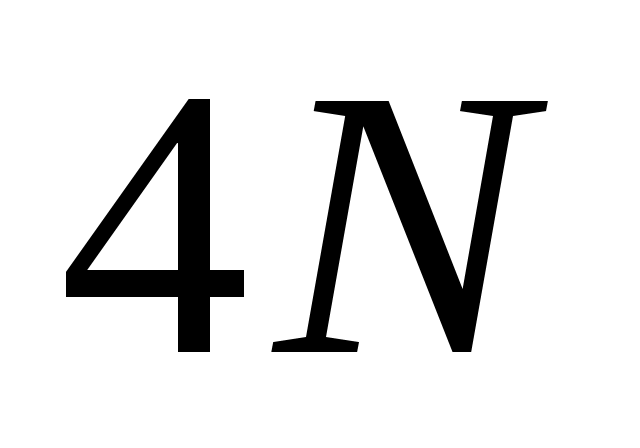 коэффициентов. Условие принадлежности сплайна классу коэффициентов. Условие принадлежности сплайна классу 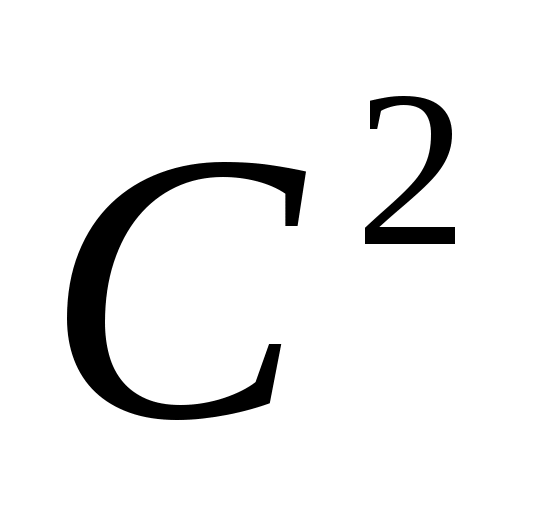 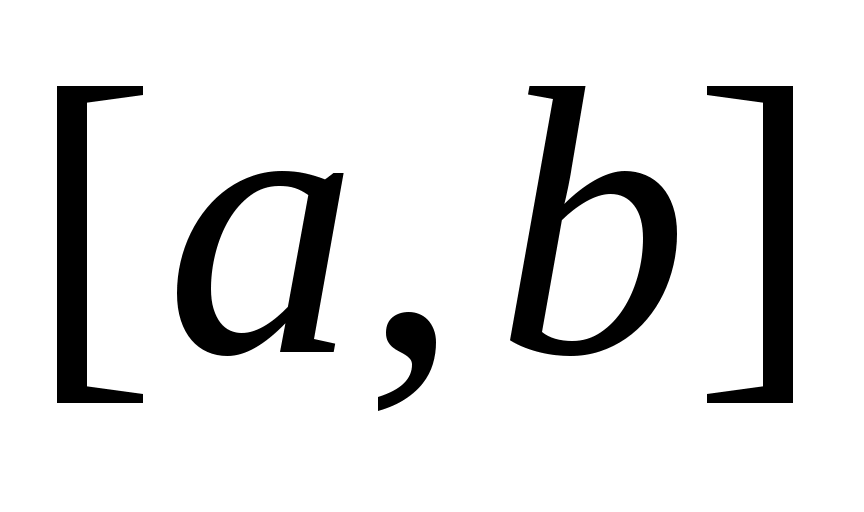 требует непрерывности во всех внутренних узлах интерполяции требует непрерывности во всех внутренних узлах интерполяции 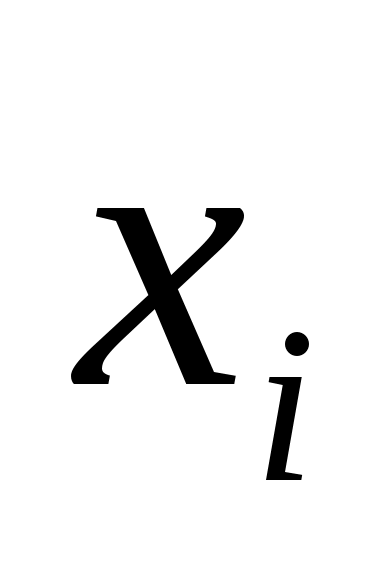 , , 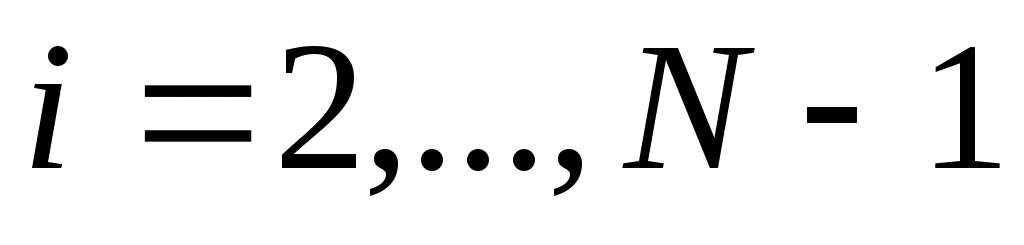 , не только сплайна , не только сплайна 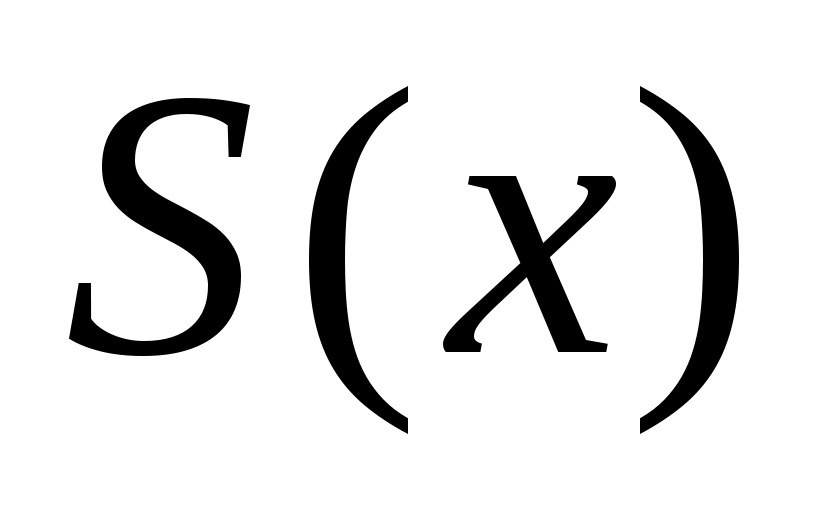 , но и его производных , но и его производных 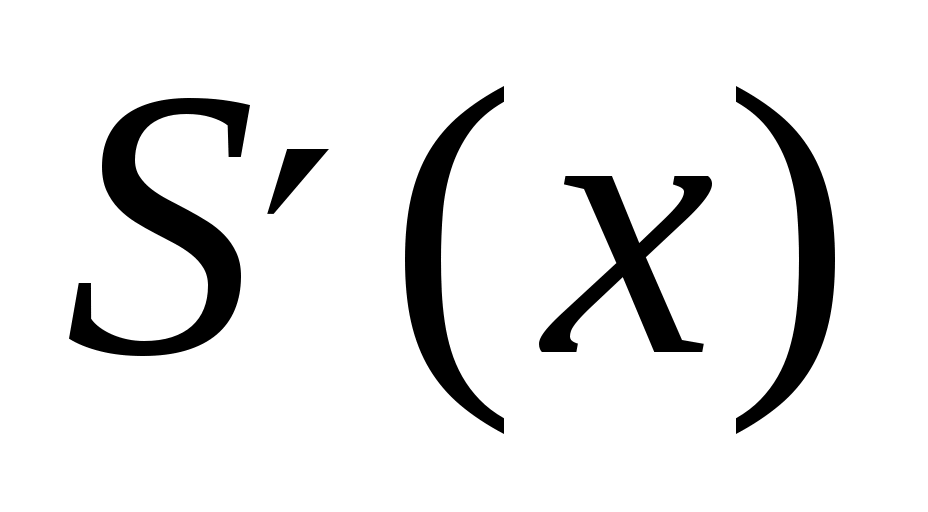 и и 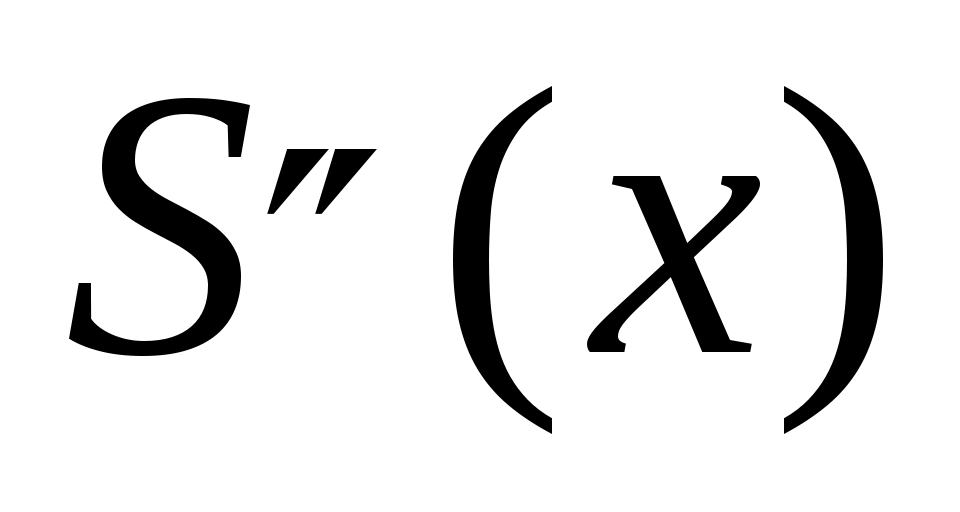 , что дает , что дает 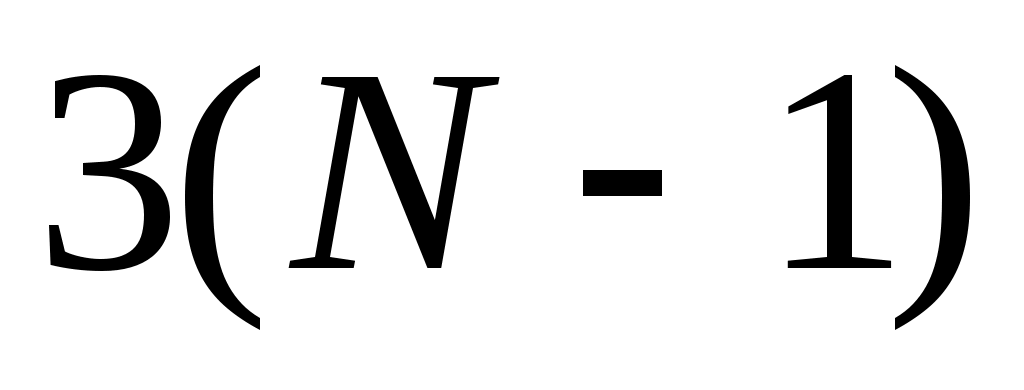 уравнений для определения неизвестных коэффициентов сплайна. Добавив уравнений для определения неизвестных коэффициентов сплайна. Добавив 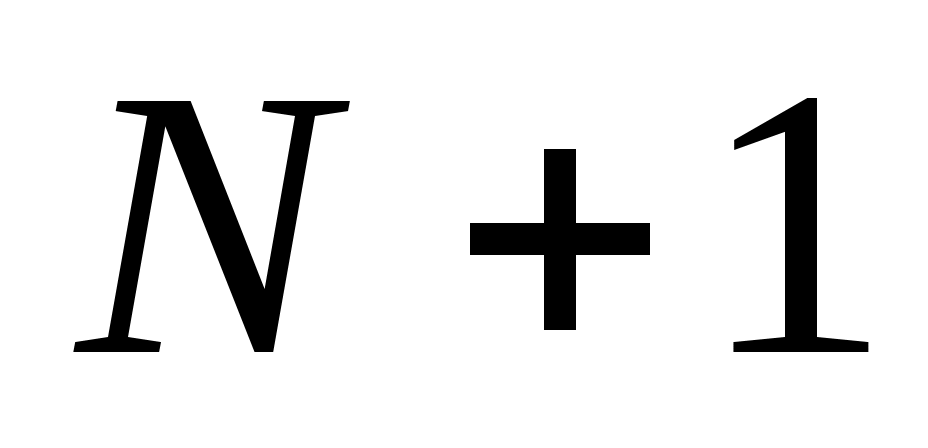 уравнение из (1), получим уравнение из (1), получим 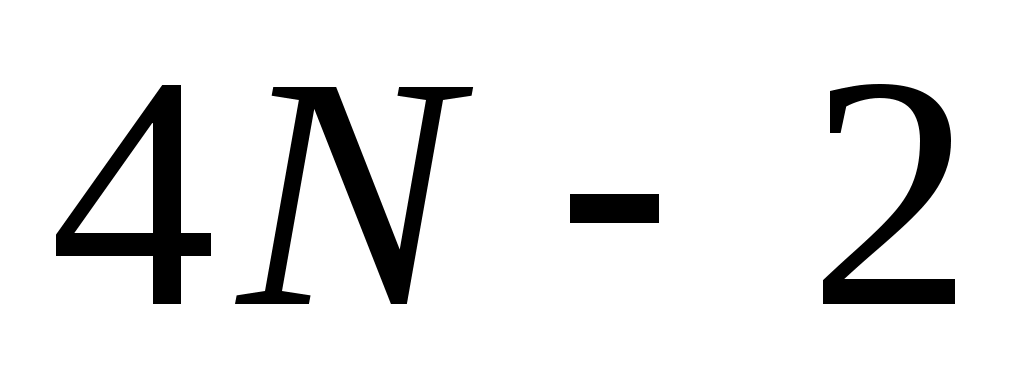 уравнения. Два недостающих уравнения обычно получают из ограничений на значение сплайна и его производных на концах промежутка уравнения. Два недостающих уравнения обычно получают из ограничений на значение сплайна и его производных на концах промежутка 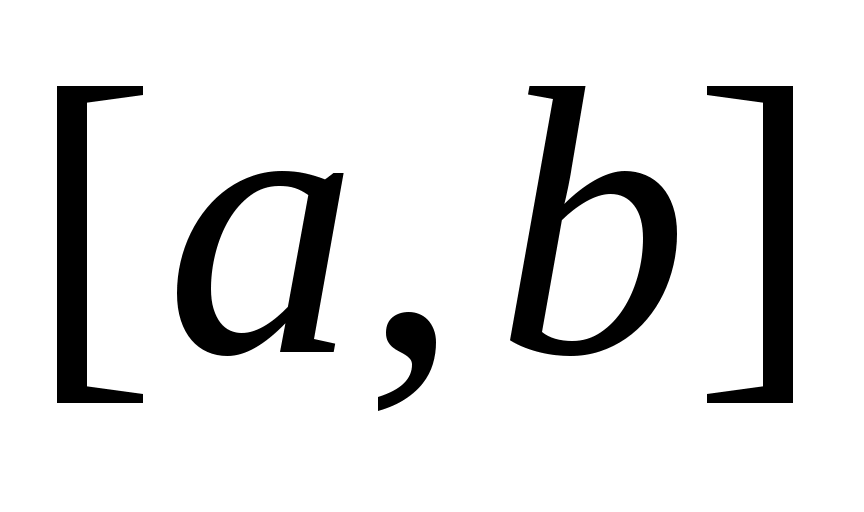 ; их называют краевыми условиями. ; их называют краевыми условиями.
Из множества различных видов краевых условий наиболее употребительными являются следующие:
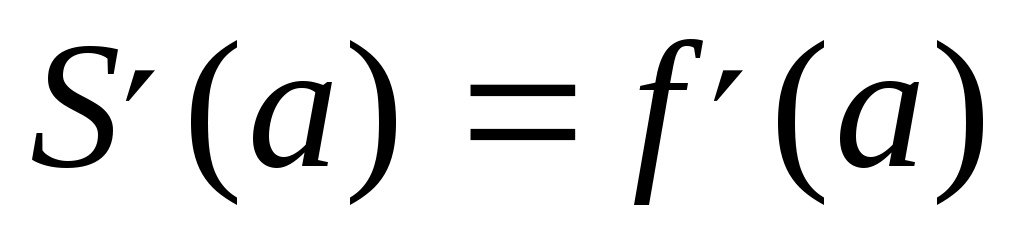 , , 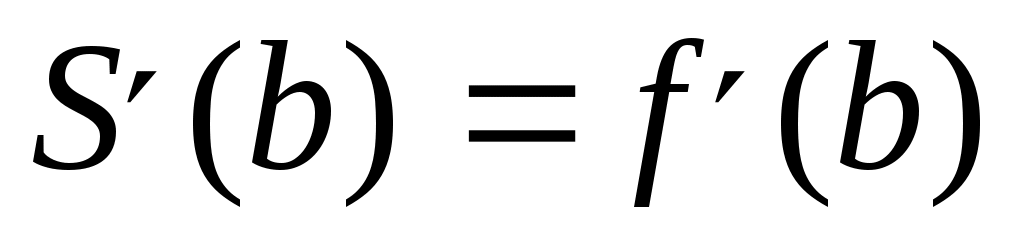 . .
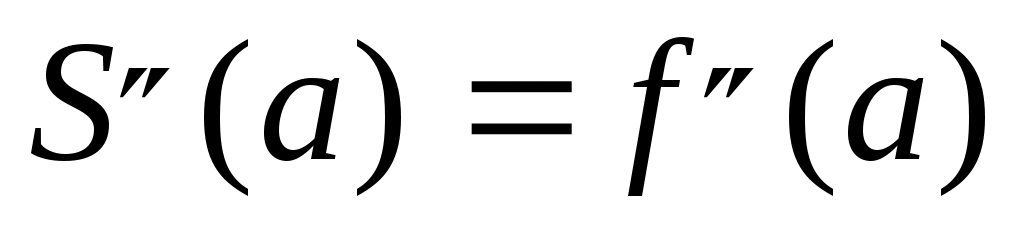 , , 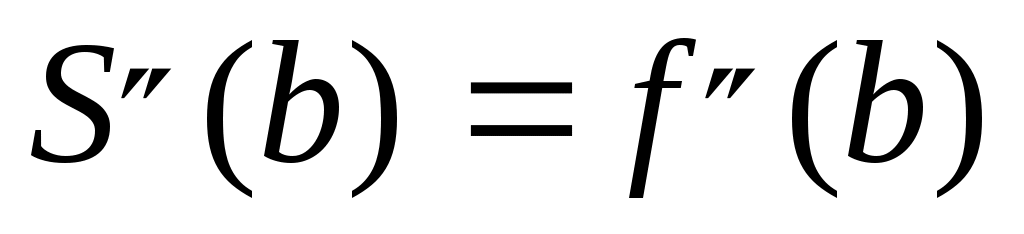 . .
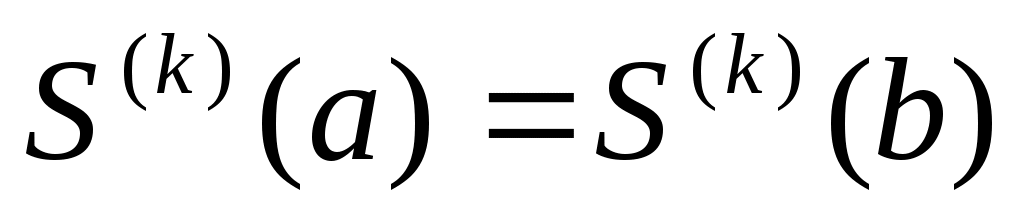 , , 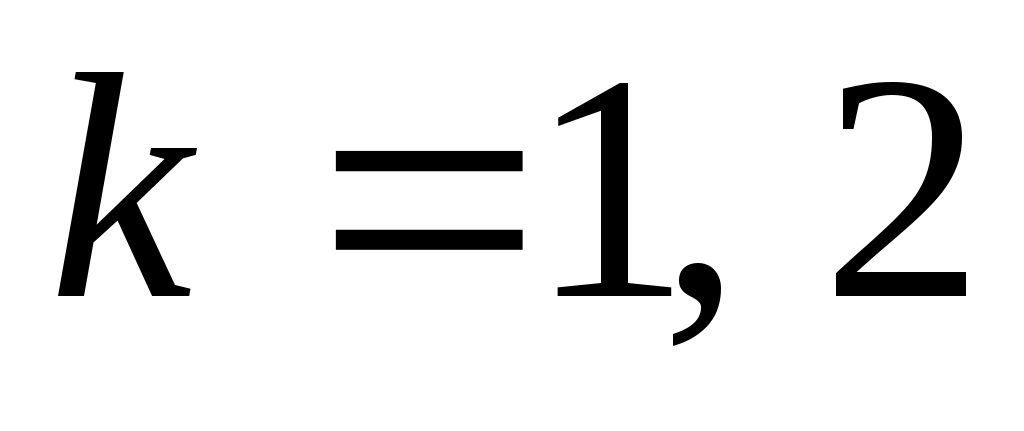 . .
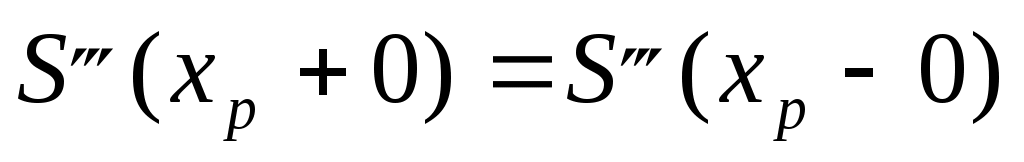 , , 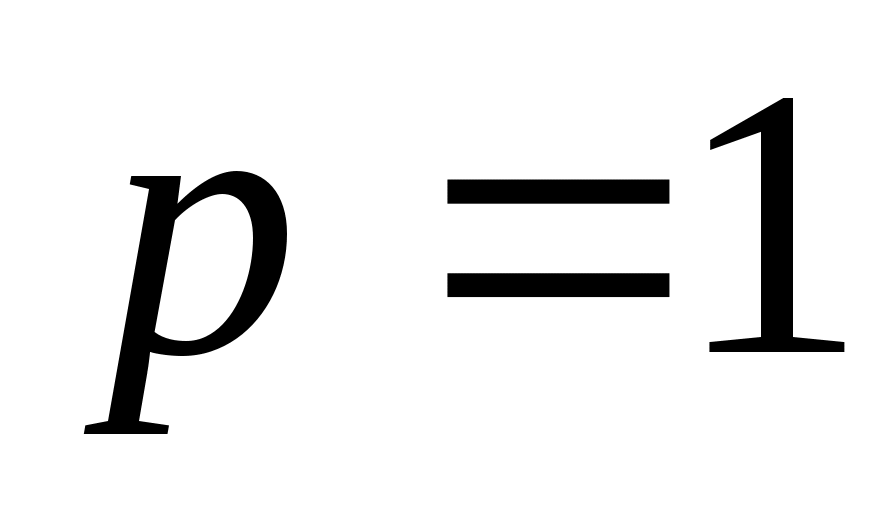 , , 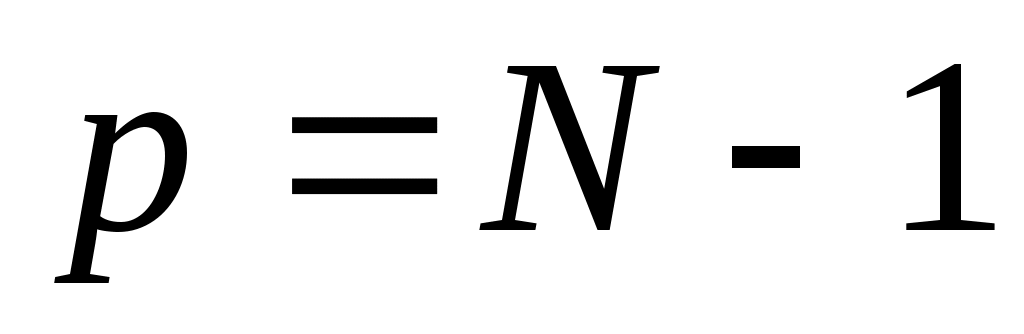 . .
Воспользуемся так называемыми «естественными» условиями, которые имеют вид
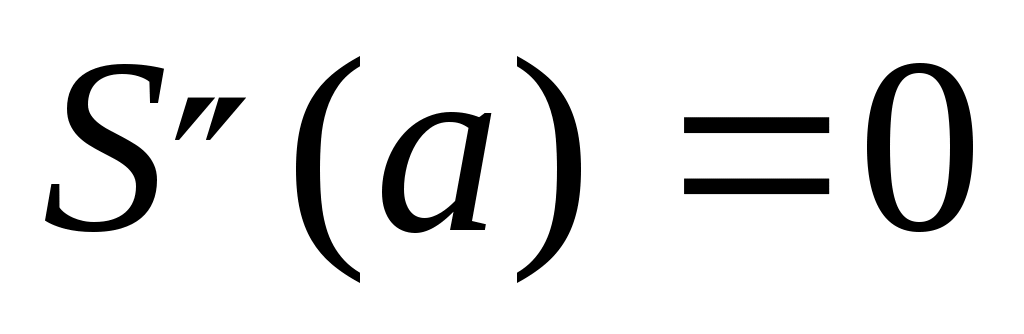 , , 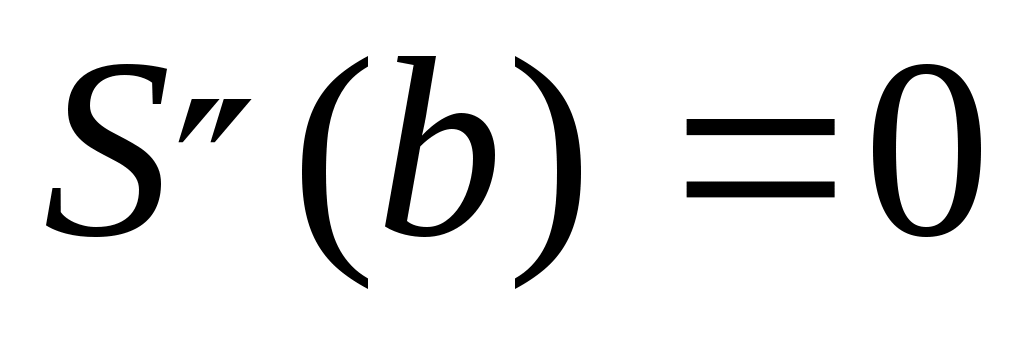 . .
Рассмотрим алгоритм построения интерполяционных кубических сплайнов. На каждом из промежутков 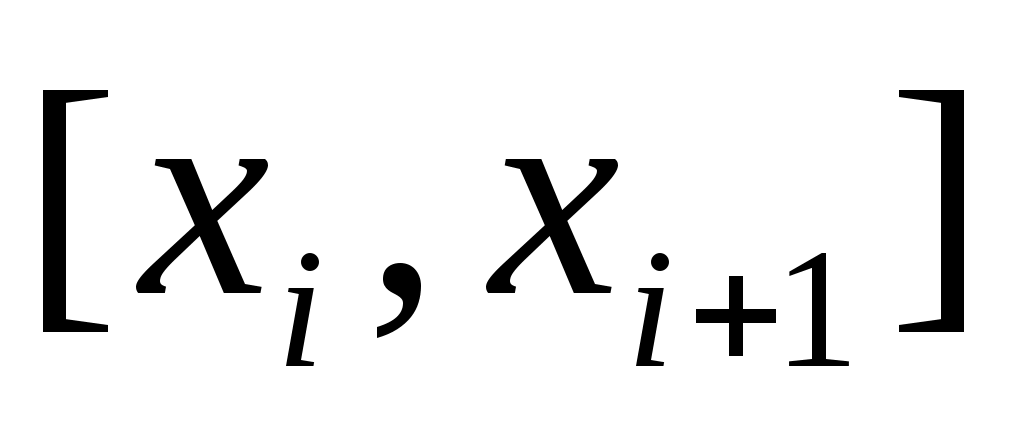 будем записывать сплайн не в общем виде будем записывать сплайн не в общем виде
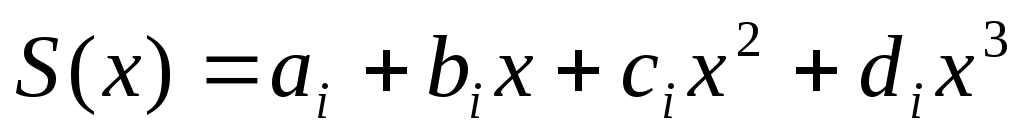 , ,
а в некотором специальном виде, позволяющем уменьшить число неизвестных коэффициентов сплайна. Для этого введем обозначения
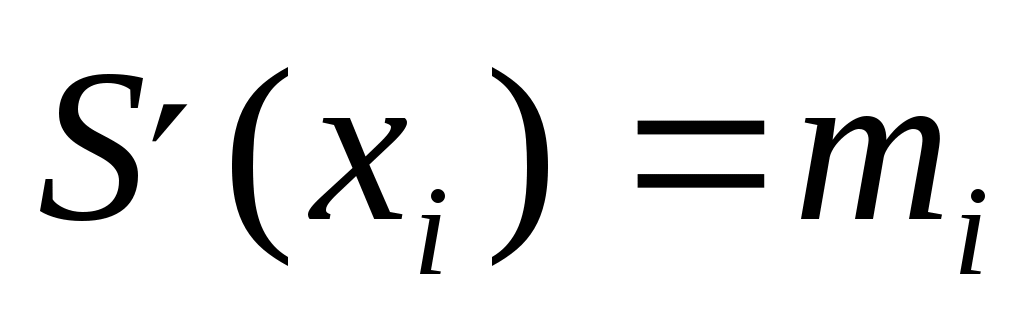 , , 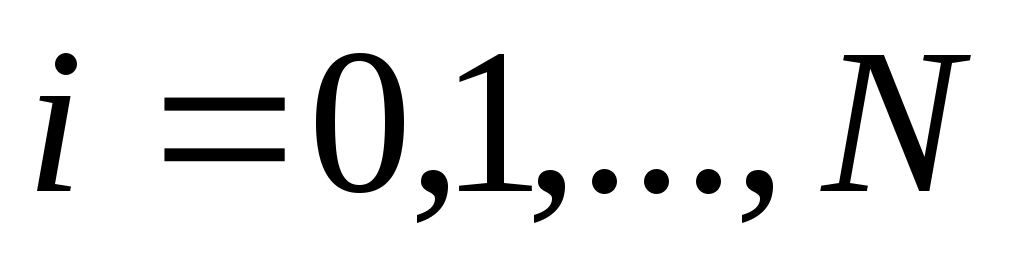 , ,
где 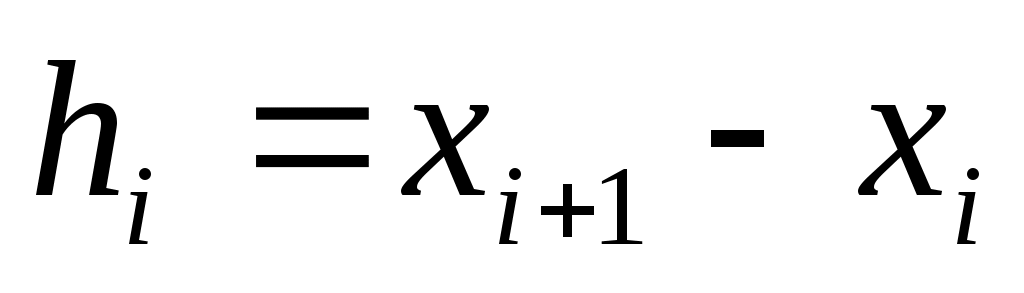 и и 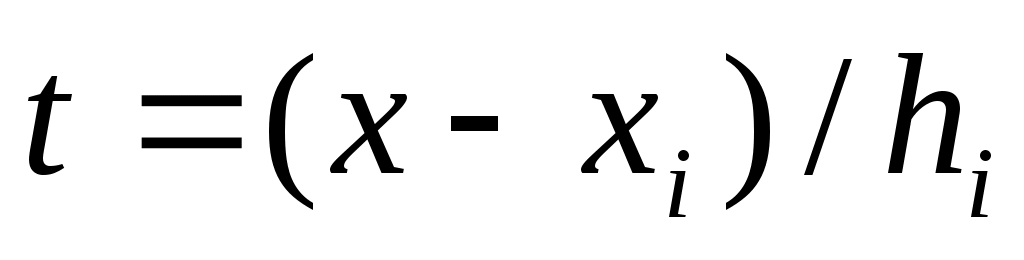 . .
На отрезке 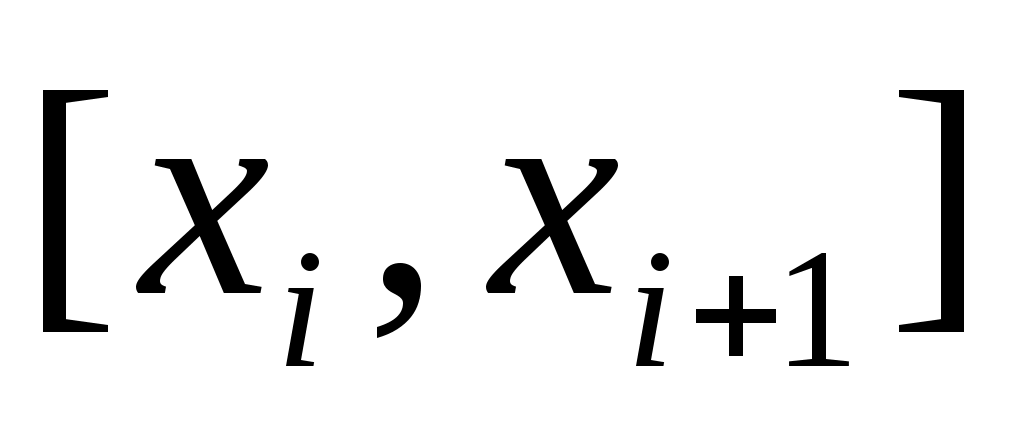 кубический сплайн можно записать в виде кубический сплайн можно записать в виде
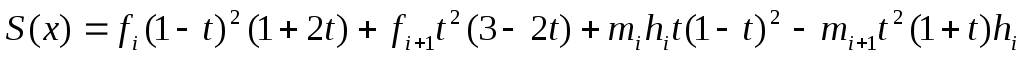 . (2) . (2)
Кубический сплайн, записанный в таком виде, на каждом из промежутков 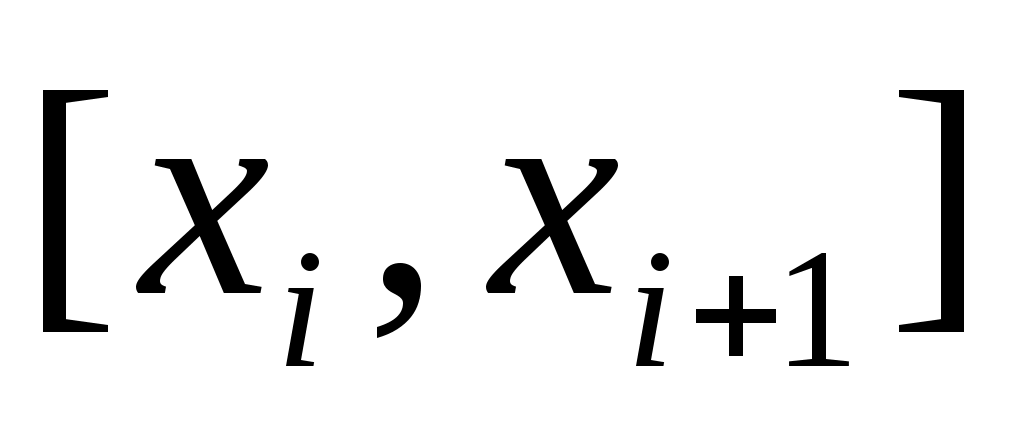 автоматически непрерывен вместе со своей первой производной всюду на автоматически непрерывен вместе со своей первой производной всюду на 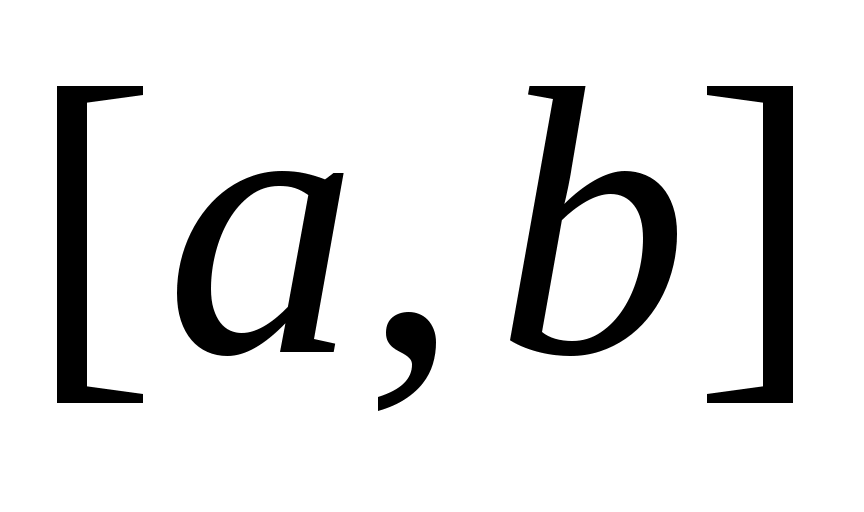 . Выберем величины . Выберем величины 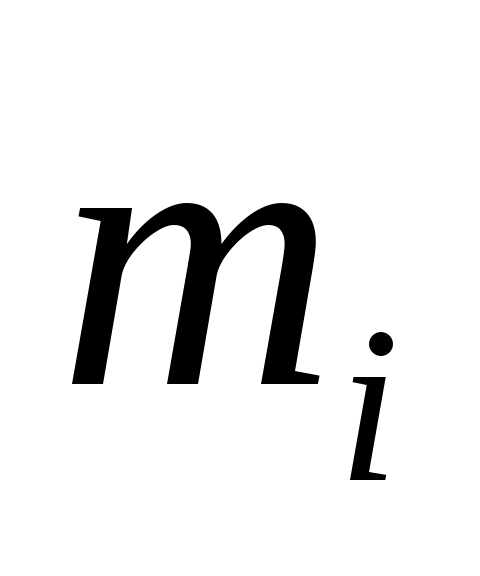 таким образом, чтобы и вторая производная была непрерывна во всех внутренних узлах. Из этого условия получим следующую систему уравнений: таким образом, чтобы и вторая производная была непрерывна во всех внутренних узлах. Из этого условия получим следующую систему уравнений:
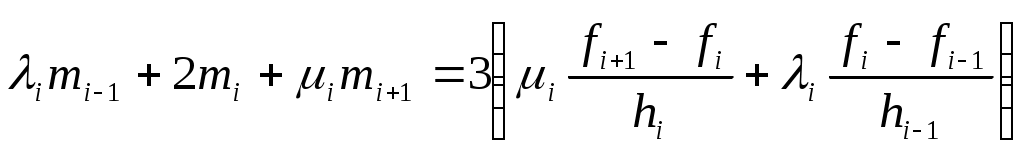 , (3) , (3)
где 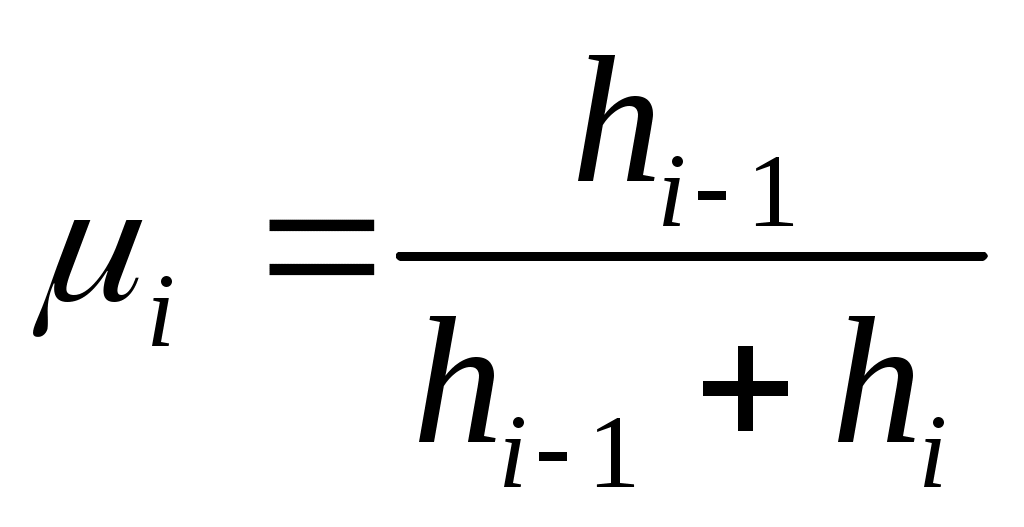 , , 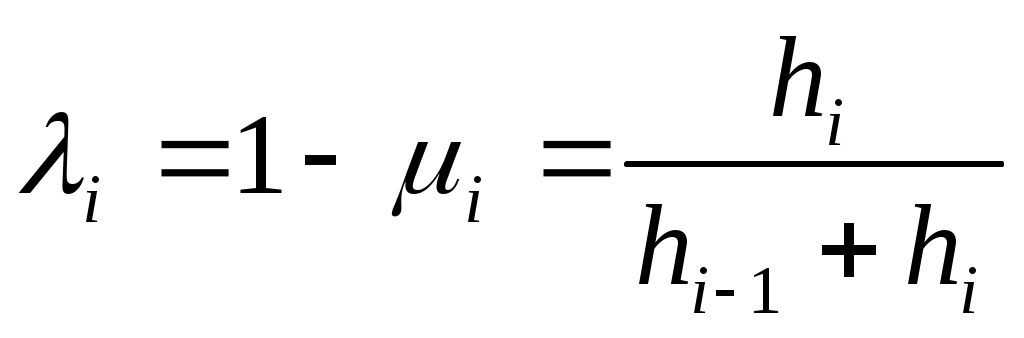 . .
К уравнения (3) следует добавить уравнения, полученные из граничных условий. В рассмотренном случае эти уравнения имеют вид
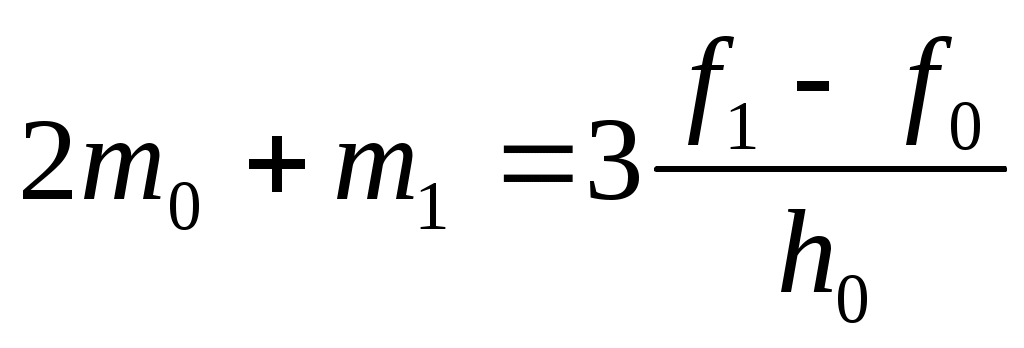 , , 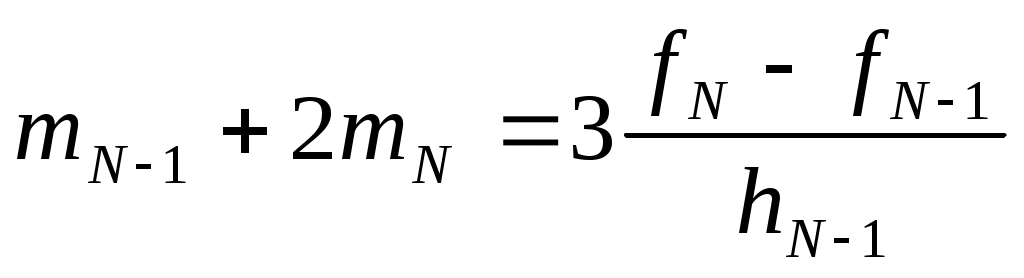 . (4) . (4)
Таким образом, задача построения кубического сплайна свелась к решению линейной системы для неизвестных коэффициентов 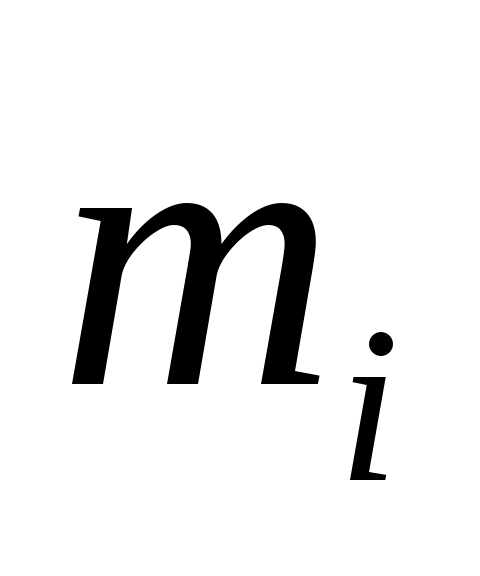 : :
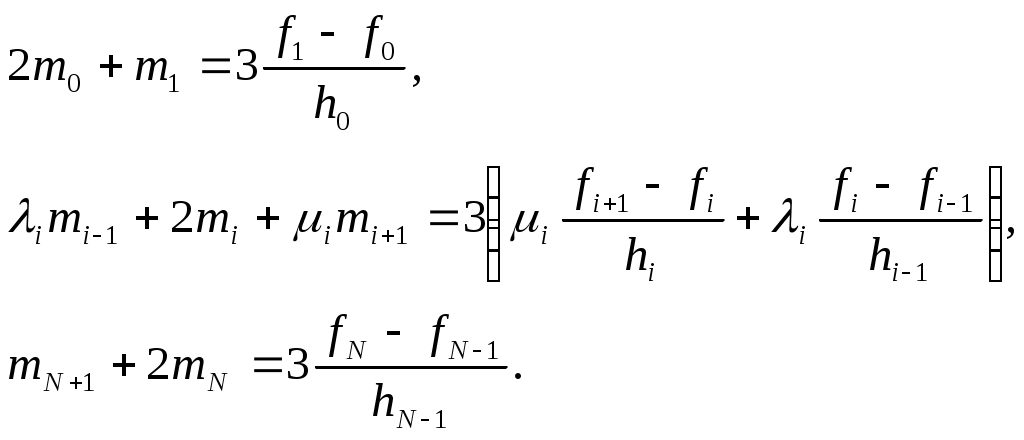 (5) (5)
Матрица системы (5) трёхдиагональная, поэтому эту систему можно решить методом прогонки.
Лабораторная работа №7 Аппроксимация функции по методу наименьших квадратов
Очень часто, особенно при анализе эмпирических данных, возникает необходимость найти в явном виде функциональную зависимость между величинами 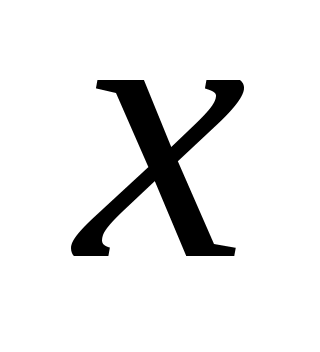 и и 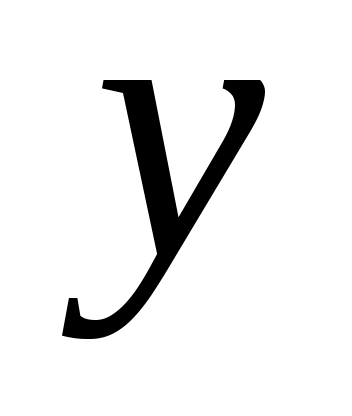 , которые получены в результате измерений. Как правило, общий вид этой функциональной зависимости известен, а некоторые числовые параметры закона неизвестны. , которые получены в результате измерений. Как правило, общий вид этой функциональной зависимости известен, а некоторые числовые параметры закона неизвестны.
Пусть, например, функция задана в виде 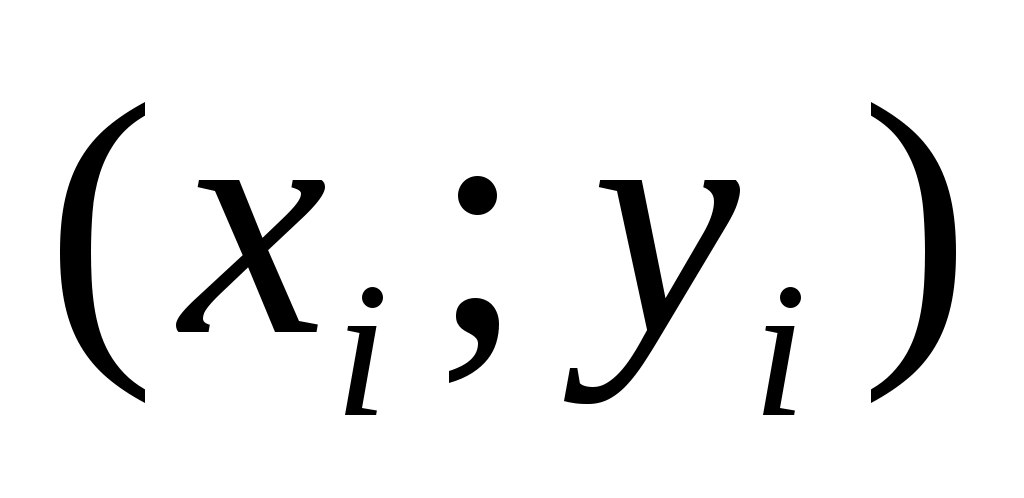 , , 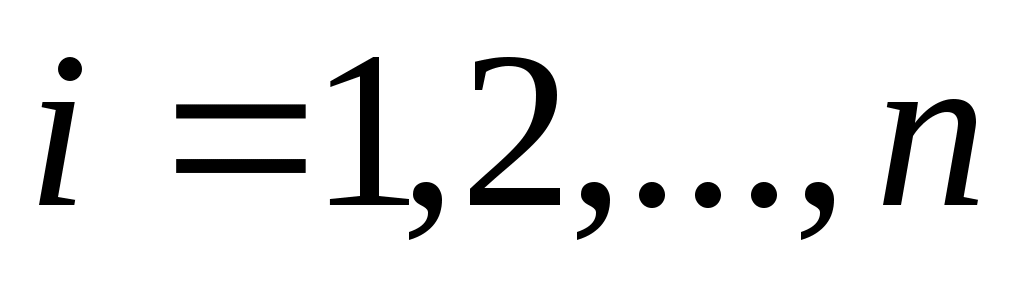 . Задача состоит в аппроксимации неизвестной функциональной зависимости между . Задача состоит в аппроксимации неизвестной функциональной зависимости между 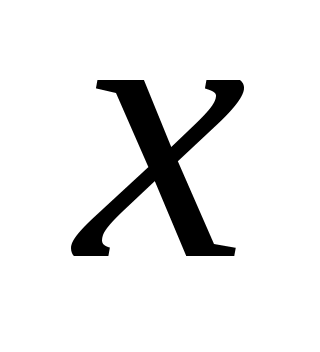 и и 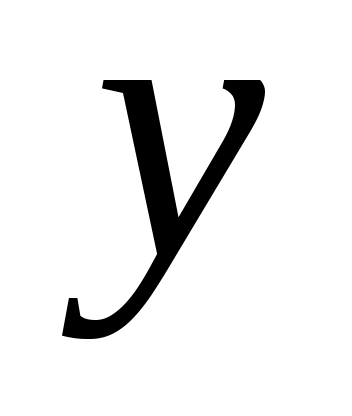 многочленом заданной степени многочленом заданной степени 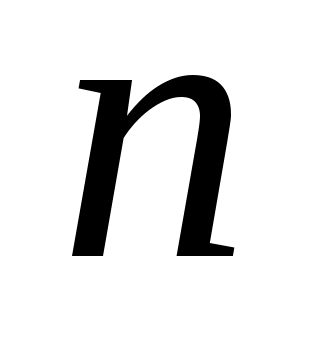 : :
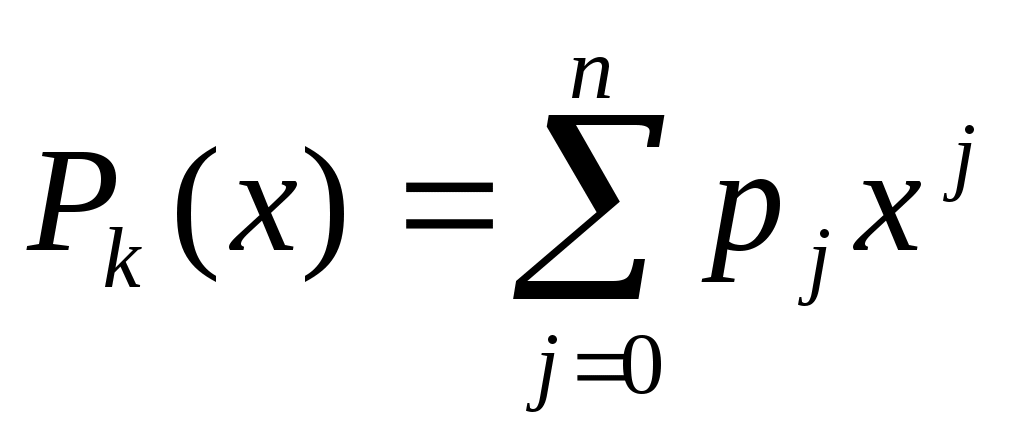 . .
Для решения этой задачи воспользуемся методом наименьших квадратов. Согласно этому методу коэффициенты многочлена нужно выбрать такими, чтобы сумма квадратов отклонений найденного многочлена от заданных значений функции была минимальной. Другими словами, коэффициенты 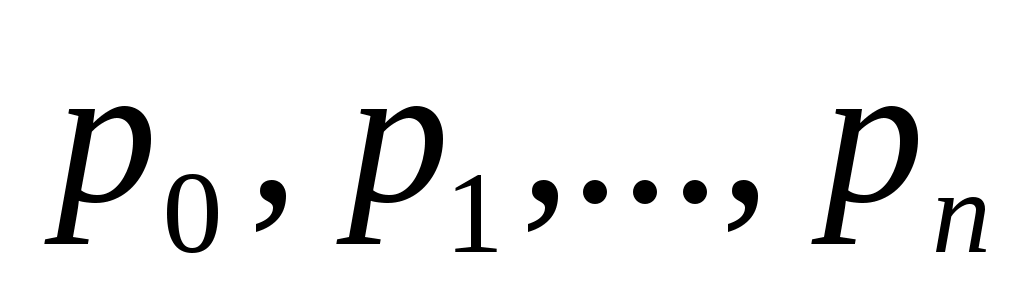 должны минимизировать функцию должны минимизировать функцию
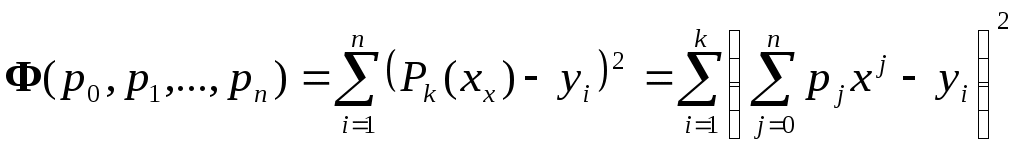 . .
В точке минимума функции 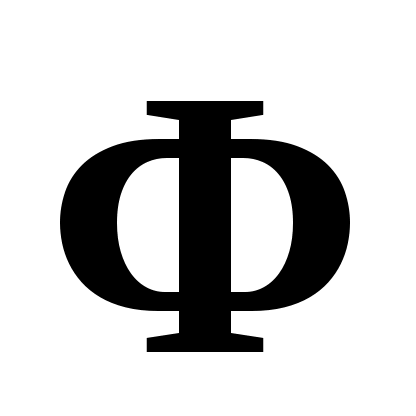 ее производные ее производные 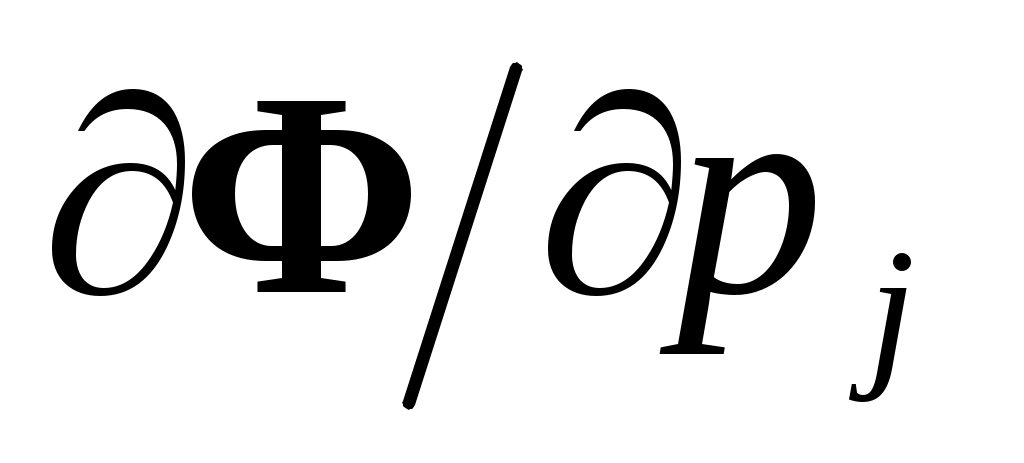 обращаются в нуль. Дифференцируя обращаются в нуль. Дифференцируя 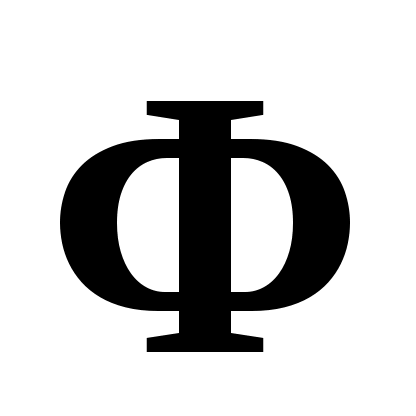 и приравнивая нулю производные, получим так называемую нормальную систему метода наименьших квадратов: и приравнивая нулю производные, получим так называемую нормальную систему метода наименьших квадратов:
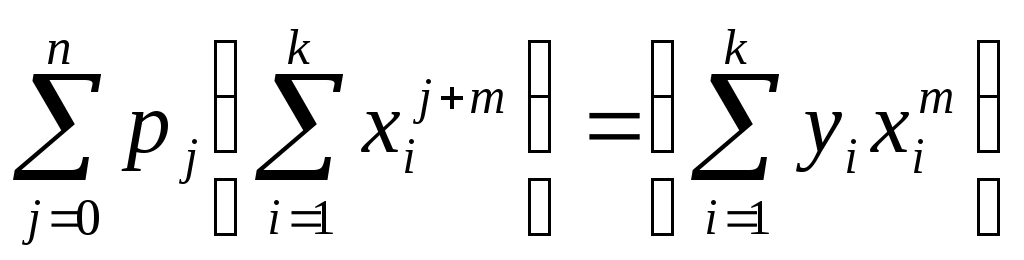 , , 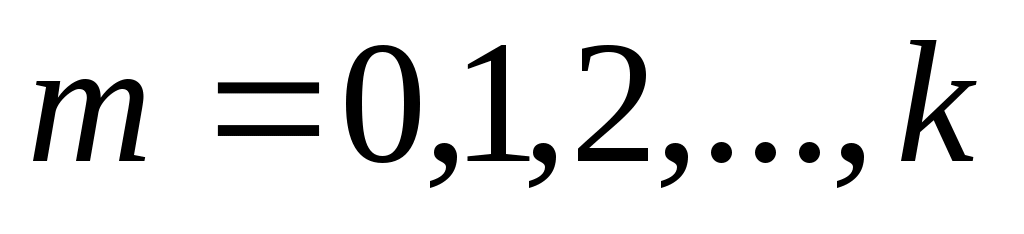 . .
Это система линейных алгебраических уравнений относительно неизвестных 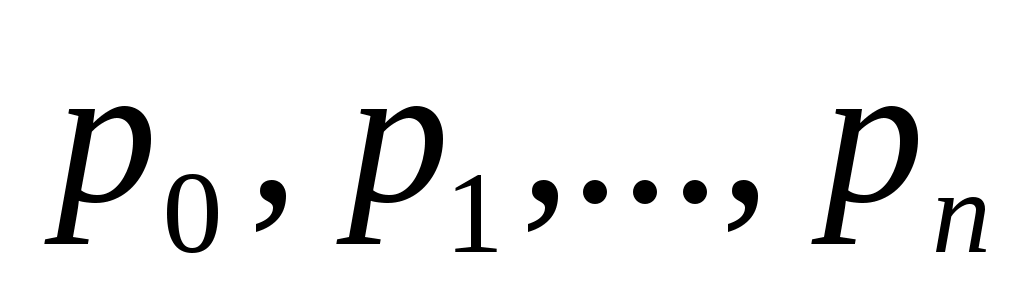 . Можно показать, что определитель этой системы отличен от нуля, т.е. решение системы существует и единственно. Однако, на практике описанную методику применяют только для нахождения многочленов, степень которых не выше четырех-пяти. При более высоких степенях нормальная система становится плохо обусловленной и погрешности определения коэффициентов велики. . Можно показать, что определитель этой системы отличен от нуля, т.е. решение системы существует и единственно. Однако, на практике описанную методику применяют только для нахождения многочленов, степень которых не выше четырех-пяти. При более высоких степенях нормальная система становится плохо обусловленной и погрешности определения коэффициентов велики.
В данной лабораторной работе заданную табличную функцию требуется аппроксимировать многочленом второй степени 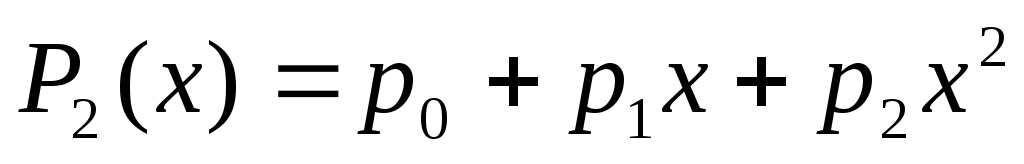 . В этом случае нормальная система имеет вид . В этом случае нормальная система имеет вид
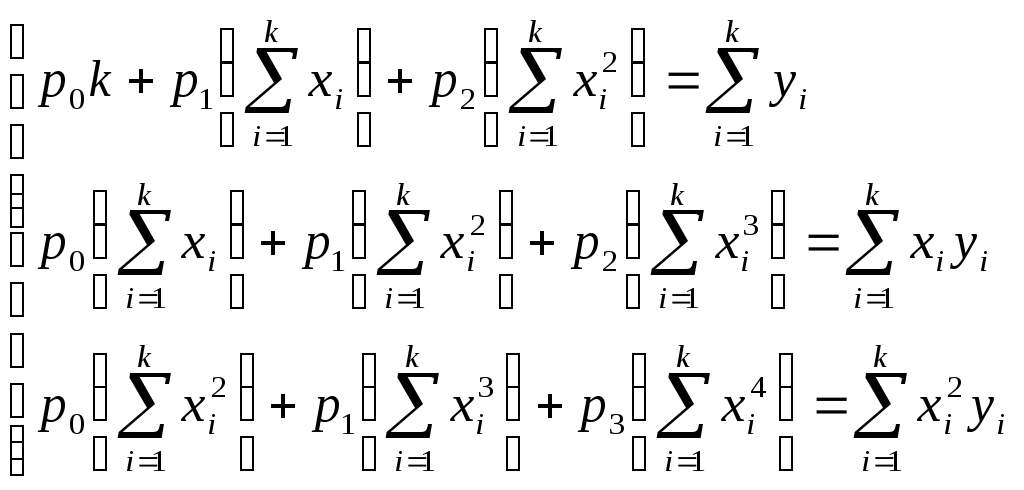
и ее можно решить, например, методом Гаусса, описанным в лабораторной работе №3.
* Корень 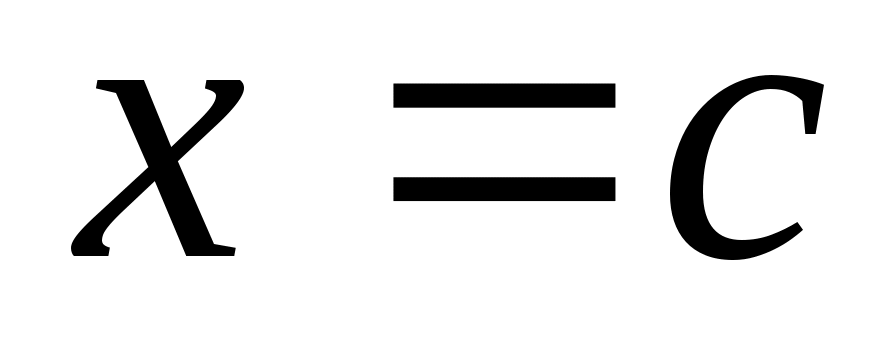 называют простым корнем дифференцируемой функции 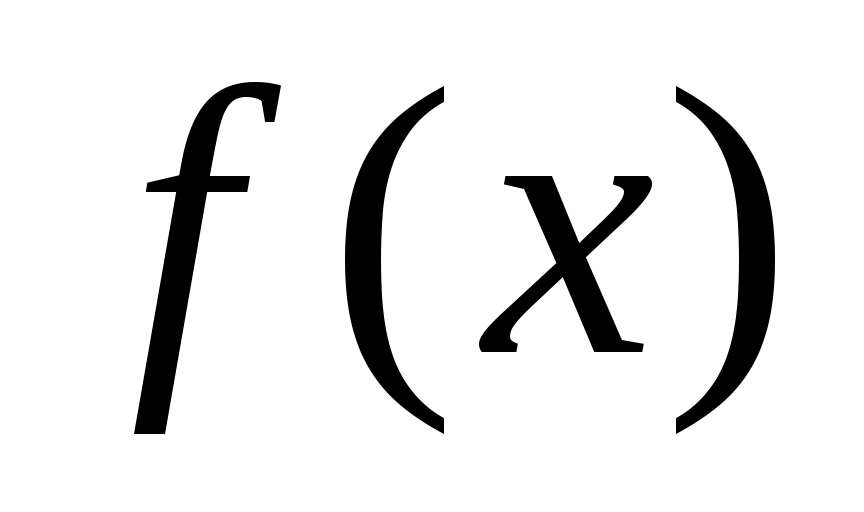 , если 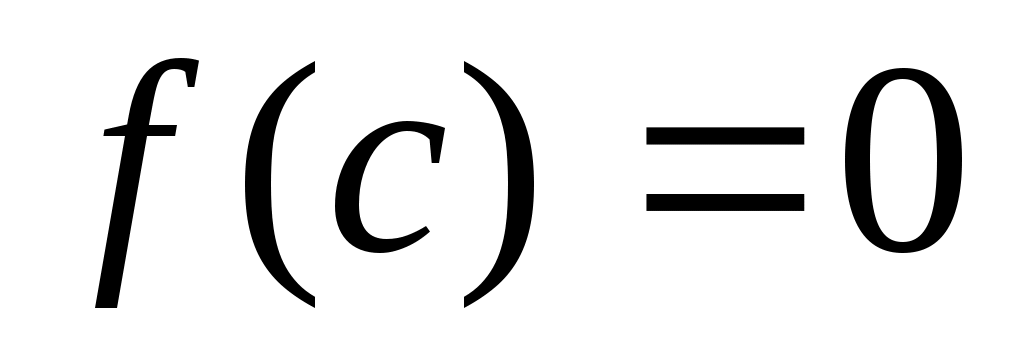 и 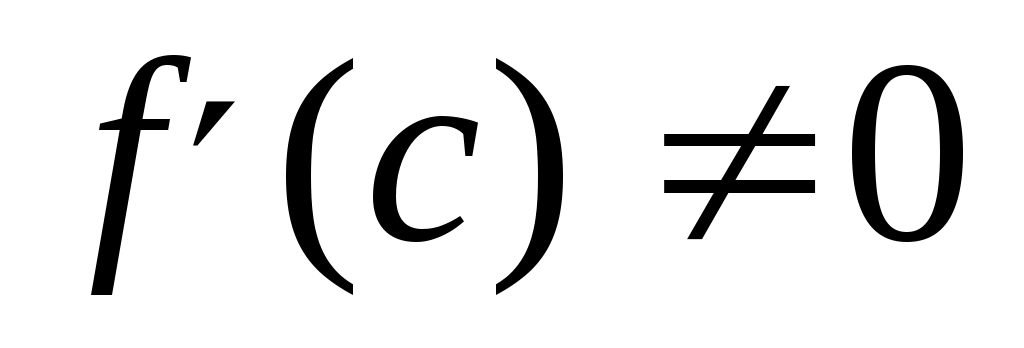 .
*) Метод численного решения задачи относят к классу точных методов, если в предположении отсутствия округлений с его помощью можно получить точное решение в результате конечного числа арифметических и логических операций.
* ) Матрица  плохо обусловлена, если малые изменения ее элементов приводят к существенным изменениям элементов матрицы 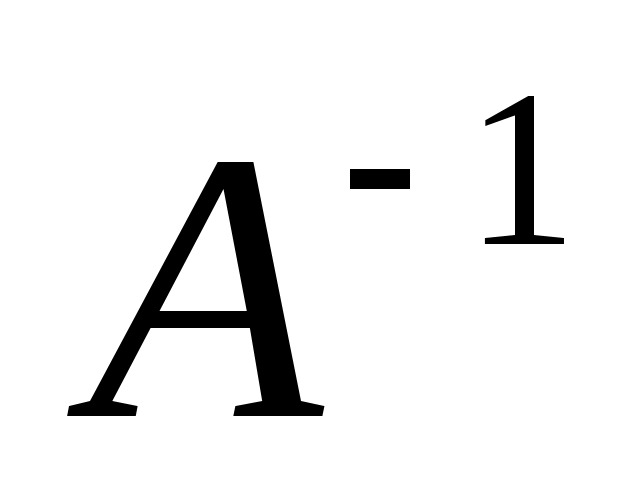 . * ) Следует заметить, что все приведенные формулы можно записать в виде 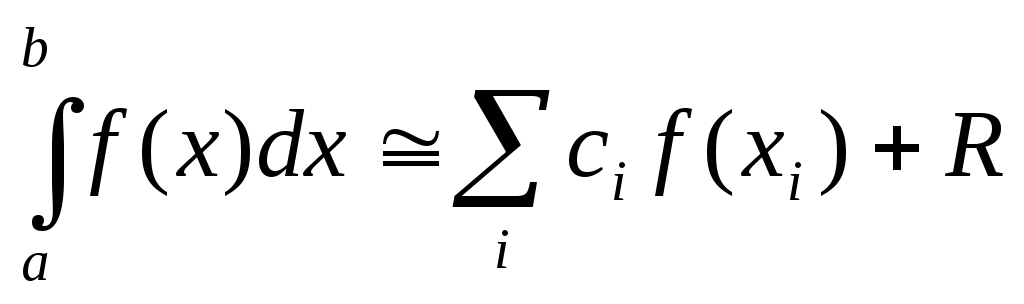 , где величины 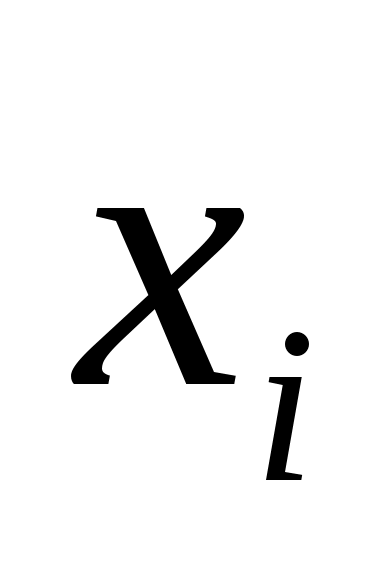 , называемые узлами, и 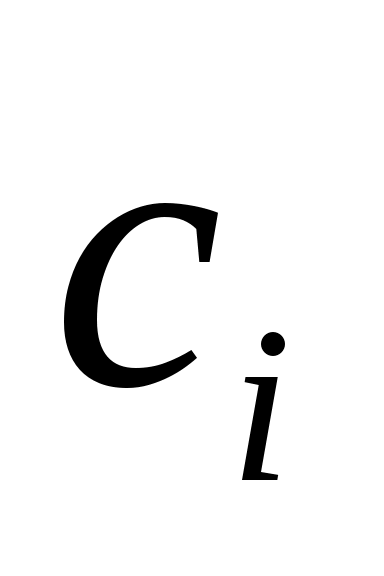 , называемые коэффициентами квадратурной формулы, не зависят от 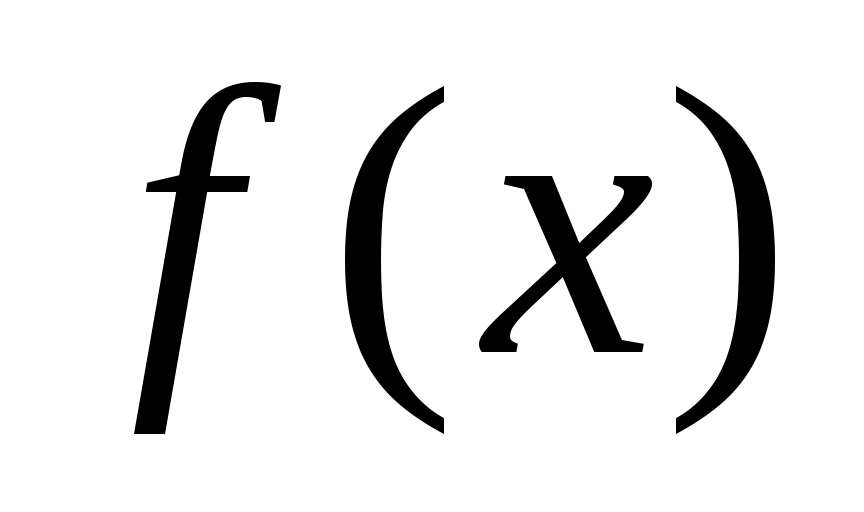 . * *) Погрешности округления носят случайный характер, и существует точка зрения, что они увеличиваются с ростом 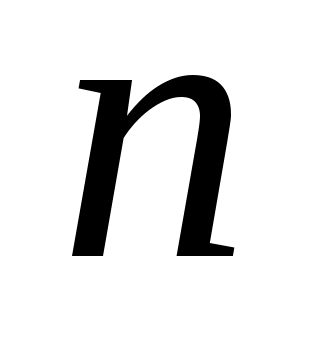 как 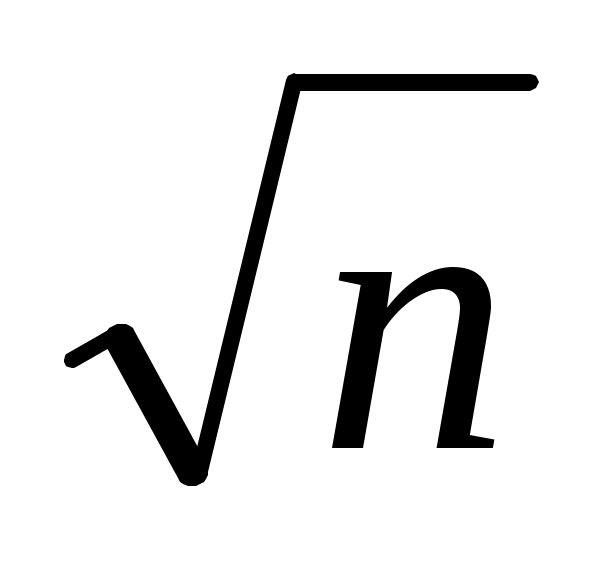 .
|
 Скачать 0.52 Mb.
Скачать 0.52 Mb.