МАТЕМАТИКА. 1 вопрос. Натуральные числа имеют вид 1,2,3 которые используют для счета предметов, людей и др. Простым
 Скачать 370.5 Kb.
|
|
1 вопрос. Натуральные числа имеют вид 1,2,3….., которые используют для счета предметов, людей и др. Простым числом называют такое натуральное число, которое больше 1 и делится только на 1 и само на себя. (2, 3, 5,7,11,13 и т.д.) Составные числа – это непростые числа больше единицы (6,8,9,12,14 ,..) Делитель- число на которое делим Кратное число – это число, делящееся на данное целое число без остатка (например, кратное 3 - 9) Наибольший общий делитель(НОД) двух и более натуральных чисел – это наибольшее из натуральных чисел, на которое делится каждое из данных чисел, например, для чисел 48 и 36 это 12. Решение : Раскладываем 36 и 48 на простые множители: 48 = 2 · 2 · 2 · 2 · 3; 36 = 2 · 2 · 3 ,затем выбираем одинаковые множители, это: 2, 2, 3; 3. перемножаем эти множители и получаем: 2 · 2 · 3 = 12 Наименьшее общее кратное двух и более натуральных чисел – это наименьшее общее число которое делится на эти числа без остатка Раскладываем 36 и 48 на простые множители: 48 = 2 · 2 · 2 · 2 · 3; 36 = 2 · 2 · 3 Берем множители из первого разложения, добавляем к ним отсутствующие множители со второго разложения и вычисляем произведение. Ответ: НОК (36; 48 ) = 2 · 2 · 2 · 2 · 3 · 3 = 144 2 вопрос Признак делимости на 2если натуральное число оканчивается четной цифрой, то это число делится без остатка на 2 (если нечетной , то число без остатка не делится на 2) Признак делимости на 3 Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3 Признак делимости на 5 число делится на пять если запись этого числа справа содержит ноль или пять Признак делимости на 9 Число делится на 9,если сумма цифр делится на 9 (Например: 1737 — сумма цифр 1 + 7 + 3 + 7 = 18. 18 делится на 9). Признак делимости на 10 Любое натуральное число, которое оканчивается на 0. 3 вопрос Целые числа (Z) - числа, которые можно записать без дробной составляющей. Рациональные числа (Q)- это числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. (Если число можно получить делением двух целых чисел, то это рациональное.число. m / n ,где числитель m — целое число, а знаменатель n — натуральное число (1,2,3,..) Правила сравнения рациональных чисел: любое положительное число больше 0 и больше любого отрицательного любое отрицательное число меньше 0 и меньше любого положительного из двух отрицательных чисел больше то, модуль которого меньше (Модуль числа– это число, равное ему самому, если число положительное, противоположному числу, если оно отрицательное) Вопрос 4 Иррациональные числа (I )- это такие числа, которые в десятичной форме записи представляют собой бесконечные непериодические десятичные дроби.(3,333333333..) Действительные числа ( R) - это любые рациональные и иррациональные числа. Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Вопрос 5 Прямую с выбранным началом отсчета, единичным отрезком и направлением называют координатной прямой Число, показывающее положение точки на прямой называют координатой этой точки Модуль числа a обозначается |a|,модуль числа всегда неотрицателен: |a|≥ 0. |6| = 6, |-3| = 3, |-10,45| = 10,45  Геометрический смысл модуляМодуль числа – это расстояние от нуля до данного числа. Например, |-5| = 5. То есть расстояние от точки -5 до нуля равно 5. Пример 1. |x – 3| = 4. Это уравнение можно прочитать так: расстояние от точки 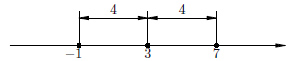 до точки  равно  . С помощью графического метода можно определить, что уравнение имеет два решения:  и  . Пример 2. Решим неравенство: |x + 7| < 4. Можно прочитать как: расстояние от точки до точки  меньше четырёх. Ответ: (-11; -3). Пример 3. Решим неравенство: |10 – x| ≥ 7. Расстояние от точки 10 до точки больше или равно семи. Ответ: (-∞; 3]υ [17, +∞) Для x≥ 0 имеем y = x. Для x < 0 имеем y = -x. График функции y = |x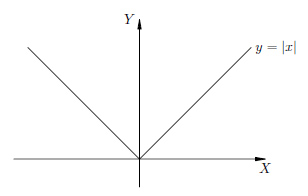 Вопрос 6 Числовое выражение– это выражение, состоящее из чисел, знаков математических действий и скобок. Например, 245 – (25: 0,5) = 195 Тождество - равенство, которое верно при любых значениях переменных. Выражение с переменными— это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.  Вопрос 7 Степень с натуральным показателем а в степени п (п – количество множителей а) арифметическим корнем n – степени из неотрицательного числа а называется такое число b, что bⁿ=a Степень с рациональным показателем Правила обращения со степенями: при умножении степени складываются приделении степени вычитаются при возведении степени в степень степени перемножаются при извлечении корня степени делятся Вопрос 7 Модуль действительного числа и его свойства . Модуль числа — это расстояние, а расстояние не может быть отрицательным.Поэтому и модуль числа не бывает отрицательным: |a| > 0 2. Модуль положительного числа равен самому числу. |a| = a, если a > 0 3. Модуль отрицательного числа равен противоположному числу. |−a| = a 4. Модуль нуля равен нулю. |0| = 0, если a = 0 5. Противоположные числа имеют равные модули. |−a| = |a| = a 6. Модуль произведения равен произведению модулей этих чисел. |a b| = |a| |b|, когда 7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя: Геометрическая интерпретация модулямодуль числа — это расстояние от нуля до данного числа. 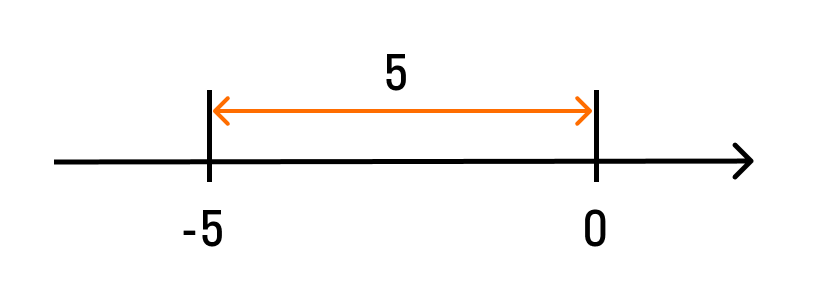 Решим уравнение: |a - 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию. 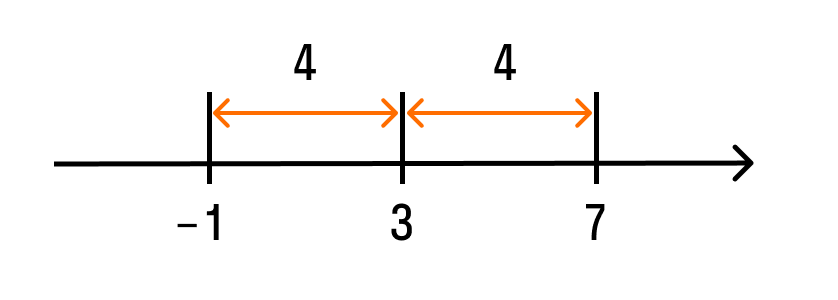 Уравнение имеет два решения: −1 и 7. Решим неравенство: |a + 7| < 4. Эту запись читаем так: расстояние от точки a до точки −7 меньше четырех. Отмечаем на числовой прямой точки, удовлетворяющие этому условию: 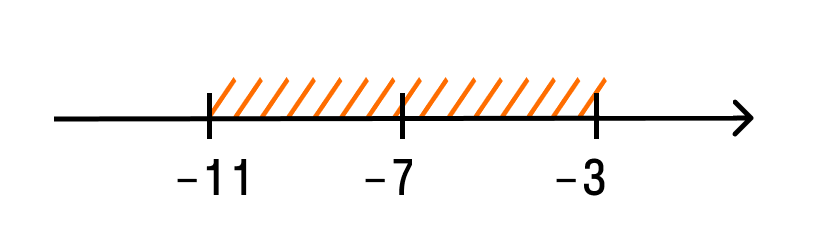 Ответ в данном случае будет таким: (−11; −3). Решим неравенство: |10 − x| ≥ 7. Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой. 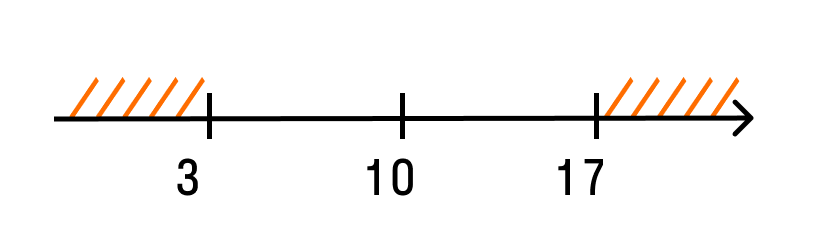 Ответ: (−∞; 3] [17, +∞). График функцииГрафик функции равен y = |х|. Для x > 0 имеем y = x; Для x < 0 имеем y = −x. В результате : 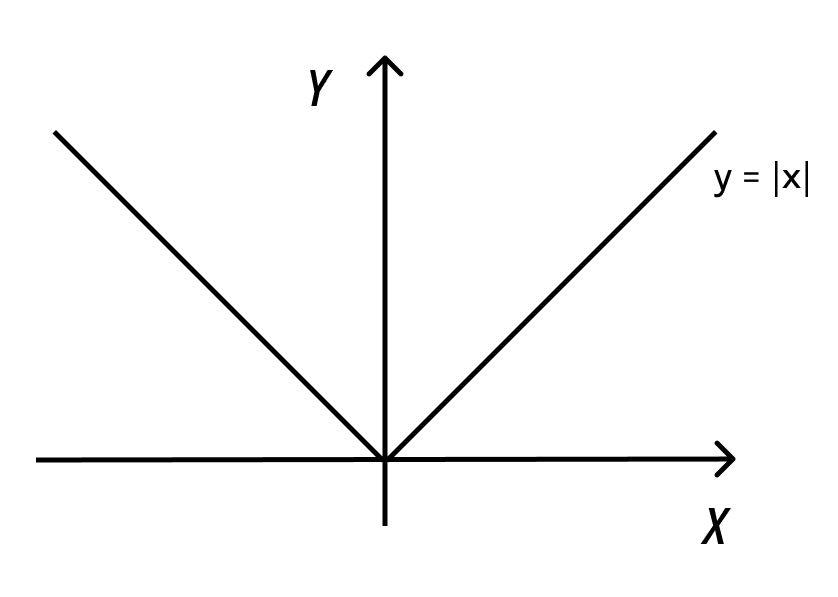 |