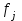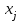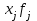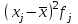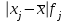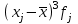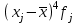статистика 6 вар. Кафедра Математика и информатика
 Скачать 128.88 Kb. Скачать 128.88 Kb.
|
 Кафедра ___Математика и информатика_________________________ Рейтинговая работа _______________________________________________ (домашняя творческая работа, расчетно-аналитическое задание, реферат, контрольная работа) по дисциплине Статистика Задание/вариант № 6 Тема* ______________________________________________________________ Выполнена обучающимся группы о.ЭЗДтс 24.2/Б2-22 Мартынов Анатолий Борисович (фамилия, имя, отчество) Преподаватель ____________________________________________________ (фамилия, имя, отчество) Москва – 2023 г. Содержание ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РЕЙТИНГОВОЙ РАБОТЫ 2 Выполнение задания работы 3 Список использованных источников 16 ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РЕЙТИНГОВОЙ РАБОТЫСкопировать данные своего варианта. Ранжировать ряд данных сортировкой по значениям от минимального к максимальному. Рассчитать количество интервалов по формуле Стерджеса, округлив вверх до целых единиц. Рассчитать величину интервала h, округлить до десятков. Рассчитать границы интервалов: Подсчитать количество единиц совокупности, принадлежащих каждому из интервалов. Построить интервальный вариационный ряд в виде таблицы Построить гистограмму распределения для интервалов и полигон распределения для вариант, кумуляту. Вычислить среднее арифметическое, моду, медиану, квартили, децили. Вычислить показатели вариации: R, dср, s2, s, Vr, Vd ,V. Вычислить асимметрию и эксцесс. Сделать вывод об однородности вариационного ряда, о симметричности и остро- или плоско-вершинности распределения. Выполнение задания работы1. Скопируем исходные данные своего варианта (варианта 6) Таблица 1 - Исходные данные
2. Ранжируем данные в порядке возрастания по значениям от минимального к максимальному Таблица 2 - Ранжированный ряд
3-7. Построим интервальный ряд распределения При построении интервального ряда с равными интервалами величина интервала h определяется по формуле: 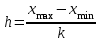 , где , гдехmax и хmin – наибольшее и наименьшее значения признака в исследуемой совокупности; k- число групп интервального ряда. При определении количества групп необходимо стремиться к тому, что бы число групп было оптимальным. Для определения числа групп используем формулу Стерждесса: k= 1 + 3,322 × lg n = 1 + 3,322 × lg 54 = 6,8 Округляем в большую сторону. Таким образом, будем строить ряд, образовав 7 групп с равными интервалами. Максимальное значение признака: 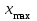 = 241 = 241Минимальное значение признака: 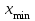 = 47 = 47Расчет величины интервалов: 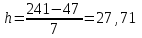 По условию задания необходимо округлить до десятков: h = 30. Сделаем 1-й и последний интервалы открытыми. Образуем следующие группы: До 70 70-100 100-130 130-160 160-190 190-220 220 и более Подсчитываем число единиц в каждой группе и получаем интервальный ряд распределения (таблица 3). Помимо частот в абсолютном выражении рассчитываем частости (относительные частоты). Таблица 3 - Интервальный ряд распределения
Вывод. Распределение единиц по группам не является полностью равномерным. Преобладают единицы со значением признака от 130 до 160. Это 14 единиц, доля которых составляет 25,9% от общего числа рассматриваемых единиц. Доля единиц с наименьшим значением признака (до 70 единиц) составляет 14,8% (8 единиц). Доля единиц с наибольшим значением признака (от 220 единиц) составляет 3,7% (2 единицы). 8. Построим графики ряда распределения Графически ряды распределения изображают в виде полигона (рисунок 1). Для построения полигона в прямоугольной системе координат на оси абсцисс откладывают значения аргумента 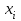 , а на оси ординат - значения частот. Далее в этой системе координат строят точки, координатами которых являются пары соответствующих чисел из вариационного ряда. Полученные точки последовательно соединяют отрезками прямой. Крайнюю «левую» точку соединяют с точкой оси абсцисс, абсцисса которой находится слева от рассматриваемой точки на таком же расстоянии, как абсцисса ближайшей справа точки. Аналогично крайнюю «правую» точку также соединяют с точкой оси абсцисс. , а на оси ординат - значения частот. Далее в этой системе координат строят точки, координатами которых являются пары соответствующих чисел из вариационного ряда. Полученные точки последовательно соединяют отрезками прямой. Крайнюю «левую» точку соединяют с точкой оси абсцисс, абсцисса которой находится слева от рассматриваемой точки на таком же расстоянии, как абсцисса ближайшей справа точки. Аналогично крайнюю «правую» точку также соединяют с точкой оси абсцисс. 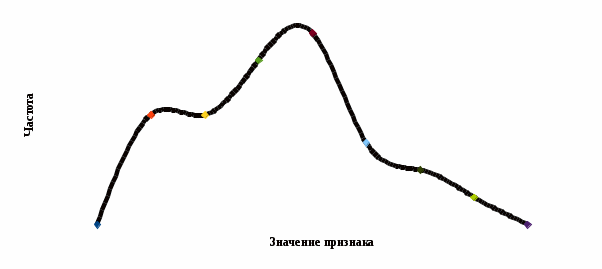 Рисунок 1 – Полигон распределения Изобразим интервальный ряд распределения в виде гистограммы (рисунок 2): 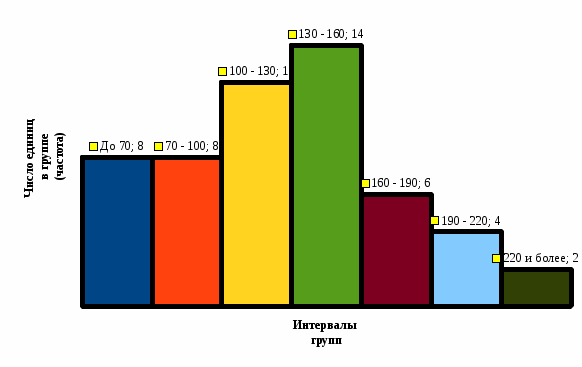 Рисунок 2 – Гистограмма распределения Кумулята строится по накопленным частотам (расчет представлен в таблице 5). Она начинается с нижней границы 1-го интервала, накопленная частота откладывается в верхней границе интервала: 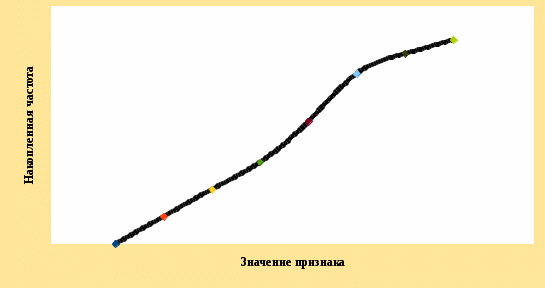 Рисунок 3 – Кумулята распределения 9. Вычислим среднее арифметическое, моду, медиану, квартили, децили Для расчета показателей строим вспомогательную таблицу 5: Для расчета среднего в интервальном ряду используется формула средней арифметической взвешенной: 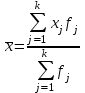 , где , гдеxj– середина j-го интервала; fj– частота j-го интервала. Расчет средней арифметической взвешенной: 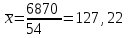 Вывод. В рассматриваемой совокупности среднее значение признака составляет 127,22 единицы. Таблица 4 - Вспомогательная таблица для расчета показателей распределения
Мода и медиана являются структурными средними величинами, характеризующими (наряду со средней арифметической) центр распределения единиц совокупности по изучаемому признаку. Мода Мо – значение признака, которое встречается наиболее часто в рассматриваемой совокупности. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую частоту). Конкретное значение моды для интервального ряда рассчитывается по формуле: 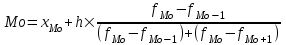 , где , гдехМo – нижняя граница модального интервала, h – величина модального интервала, fMo– частота модального интервала, fMo-1 – частота интервала, предшествующего модальному, fMo+1 – частота интервала, следующего за модальным. Согласно данным модальным интервалом ряда является интервал 130-160, так как его частота максимальна (f4= 14). Расчет моды: 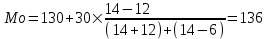 Вывод. Для рассматриваемой совокупности наиболее часто встречаются значения признака равные 136 единицы. Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности. Конкретное значение медианы для интервального ряда рассчитывается по формуле: 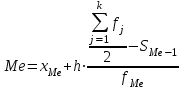 , где , где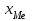 – нижняя граница медианного интервала, – нижняя граница медианного интервала,h – величина медианного интервала; 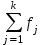 – сумма всех частот ряда; – сумма всех частот ряда;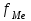 – частота медианного интервала; – частота медианного интервала;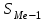 – сумма частот, накопившихся до начала медианного интервала. – сумма частот, накопившихся до начала медианного интервала.Медианным интервалом является интервал 100-130, так как именно в этом интервале накопленная частота S3 =28 впервые превышает величину, равную половине совокупности (0,5·54 = 27). Расчет медианы: 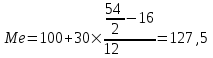 Вывод. В рассматриваемой совокупности половина значение признак не менее 127,5 единиц, а другая половина – не более 127,5 единиц. 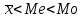 , следовательно, асимметрия левосторонняя. В совокупности преобладают единицы с более высокими значениями признака, чем среднее значение. , следовательно, асимметрия левосторонняя. В совокупности преобладают единицы с более высокими значениями признака, чем среднее значение.Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1и Q2; 25% - между Q2и Q3; остальные 25% превосходят Q3. 0-й квартиль – минимальное значение признака; 2-й квартиль – медиана; 1-й и 3-й квартиль рассчитываются аналогично медиане. Значение Q1 будет там находиться в интервале 700-100, т.к. именно в этом интервале накопленная частота 16 впервые превышает четверть суммы частот 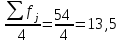 . .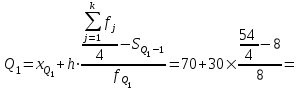 120,63 120,63Значение Q3 будет там находиться в интервале 130-160, т.к. именно в этом интервале накопленная частота 42 впервые превышает три четверти суммы частот 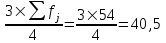 . .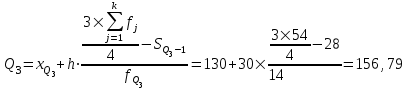 Децили делят совокупность на 10 равных частей. Рассчитываются аналогично медиане и квартилям. Интервалом 1-го дециля d1 будет является интервал 40-70 (до 70), т.к. именно в этом интервале накопленная частота 8 впервые превышает 1/10 суммы частот 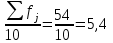 . .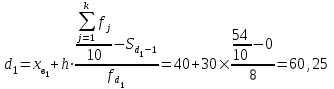 Интервалом 9-го дециля d9 будет интервал 190-220 т.к. в этом интервале накопленная частота 52 впервые превышает 9/10 суммы частот 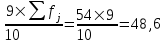 . .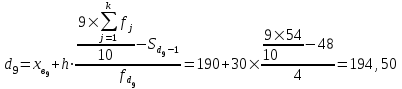 10. Вычислим показатели вариации Размах вариации характеризует амплитуду колебаний значений признака, рассчитывается как разность максимального и минимального значения признака. По исходным данным (таблица 1) размах вариации: 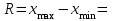 241 – 47 = 194 241 – 47 = 194Среднее линейное отклонение: 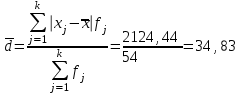 Дисперсия: 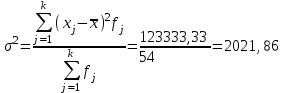 Среднее квадратическое отклонение: 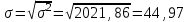 Вывод. Отклонение от среднего значения признака в ту или иную сторону составляет 44,97 единиц. Коэффициент вариации является мерой относительной колеблемости признака около средней и характеризует степень однородности признака в изучаемой совокупности: 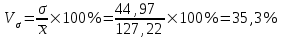 Вывод. Значение коэффициента вариации не превышает 40%, следовательно, вариация признака в исследуемой совокупности единиц незначительная. Однако значение коэффициента вариации больше 33,3%. это говорит о том, что совокупность не однородна. Найденное среднее значение не является типичной и надежной характеристикой среднего. Относительное линейное отклонение 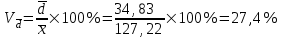 Коэффициент осцилляции: 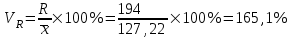 Вывод. Доля среднего линейного отклонения в среднем значении признака составляет 27,4%. Доля размаха вариации в среднем значении – 165,1%. 11. Рассчитаем показатели асимметрии и эксцесса Установлена следующая оценочная шкала асимметричности для коэффициента асимметрии Пирсона: |As| 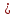 0,25 - асимметрия незначительная; 0,25 - асимметрия незначительная;0,25<|As| 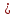 0,5 - асимметрия заметная (умеренная); 0,5 - асимметрия заметная (умеренная);|As|>0,5 - асимметрия существенная. Расчет коэффициента асимметрии Пирсона: 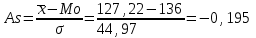 Вывод. Значения коэффициента асимметрии Пирсона отрицательное, что означает незначительную левостороннюю асимметрию распределения. Это означает, что в совокупности преобладают значения признака, более чем среднее. Расчет коэффициента асимметрии: 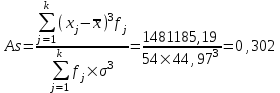 Расчет коэффициента эксцесса: 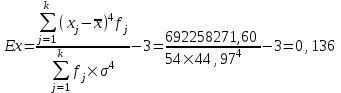 Вывод. Показатель эксцесса положительный, т.е. вершина кривой распределения лежит выше вершины кривой нормального закона распределения, а форма кривой более островершинная по сравнению с кривой нормального закона. Это означает, что значения признака концентрируются в центральной части ряда, а не рассеяны по всему диапазону. Список использованных источниковГусаров В.М. «Статистика». Учебное пособие для вызов. – М.: ЮНИ-ТИ-ДАНА, 2008, 463 с. Денисенко Р.М., Метелёв И.С. Статистика предприятия торговли: Учебное пособие. – Омск: Издатель Васильев В.В., 2007. - 108 с. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. – М.: ИНФРА – М, 2009. – 416 с. Рудакова Р.П., Букин Л.Л., Гаврилов В.И. Статистика. 2-е изд. – сПб.: Питер, 2007. – 288 с.: ил. Статистика: Учебное пособие / И.Е. Теслюк В.А. Тарловская, И.Н. Терлиженко и др., 2-е изд. – Мн: Ураджай, 2007 – 360 с., ил. Теория статистики: Учебник / Под ред. проф. Г.Л. Громыко. – 2-е изд., перераб. и доп. – М.: ИНФРА-М, 2006 – 476 с. Теория статистики: Учебник / Р.А.Шамойлова, В.Г.Минашкин, Н.А.Садовникова, Е.Б.Шувалова; Под ред. Р.А.Шамойловой. – 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2006. – 656. |