К.р №1вариант 5. Статистическая сводка. Группировка данных 3
 Скачать 434 Kb.
|
|
Вариант 5 Содержание Раздел 1. Статистическая сводка. Группировка данных 3 Задание 1 3 Задание 2 11 Раздел 2. Абсолютные и относительные показатели 17 Задание 1 17 Раздел 4. Ряды динамики 21 Задание 1 21 Раздел 5. Индексный метод 27 Задание 1 27 Раздел 6. Статистическое изучение взаимосвязей 30 Задание 1 30 Список источников 33 Раздел 1. Статистическая сводка. Группировка данныхЗадание 1По исходным данным варианта, построить интервальный ряд распределения по группировочному признаку. Группировку провести с равными интервалами, выделив четыре или пять групп, исходные данные округлить, если это необходимо для упрощения расчетов. Для целей анализа вариации признака применить показатели центра распределения, к которым относятся средняя арифметическая, мода и медиана. Для характеристики формы распределения рассчитать показатели асимметрии и эксцесса. Проанализировать полученные значения показателей центра распределения и формы распределения. Сформулировать вывод. Для варианта 2 группировочный признак - запасы, номера предприятий: с 5 по 34. Таблица 1 Группировочный признак (запасы, тыс. руб.)
Величина интервала группировки (d) определяется по формуле: d=(Xmax-Xmin)/k, где k - количество групп Хmax - максимальное значение группировочного признака Хmin - минимальное значение группировочного признака Xmin=6532 Xmax=84013 d=(84013-6532)/5=15496,20 Далее определим границы для каждой группы. Определение границ групп осуществлено таблице 2. Таблица 2 Значения границ интервалов для проведения группировки
В результате подсчета числа предприятий в каждой группе получим ряд распределения предприятий по объему запасов, представленный в таблице 3. Таблица 3 Группировка предприятий по объему запасов
Рассчитаем показатели центра распределения:  , Мо, Ме.В интервальном ряду среднее значение признака ( ) рассчитывается по формуле средней арифметической взвешенной: x'i - середина интервала i fi - частота интервала i Значения сумм x'i*fiи fi рассчитаны в таблице 4 Таблица 4 Расчет значений сумм x'i*fi, fi и (x'i- )2*fi
=970770/30=32359,000 (тыс. руб.) – средний объем запасов предприятия в выборочной совокупностиМедиана (Мe) - это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньше, чем медиана, а другая - большие. В интервальном вариационном ряду порядок нахождения медианы следующий. Для ранжированного ряда определяются накопленные частоты, по данным о накопленных частотах находится медианный интервал. Медиана делит численность ряда пополам, следовательно, она находится в том интервале, для которого накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины численности совокупности. Для анализируемого ряда медиана расположена в интервале 22028,2 -37524,40, так как для этого интервала сумма накопленных частот, равная 22, больше половины всей суммы частот (30/2=15), а накопленная частота в непосредственно предшествующем интервале (12) меньше половины всей суммы частот. Расчет значения медианы осуществляется по следующей формуле:  xMe - нижняя граница медианного интервала iMe - величина медианного интервала f/2 - полусумма частот ряда SMe-1 - сумма накопленных частот, предшествующих медианному интервалу fMe - частота медианного интервала  26677,060 (тыс. руб.)Модой (Мо) называется чаще всего встречающееся в совокупности значение признака. Для определения моды в интервальном ряду с равными интервалами сначала определяют модальный интервал, которому соответствует максимальная частота. Для анализируемых данных наибольшую частоту (12) имеет интервал 6532-22028,20. Значение моды внутри интервала определяется по формуле:  xМо - нижняя граница модального интервала hМо - длина модального интервала fМо - частота модального интервала fМо-1 - частота интервала, предшествующего модальному fМо+1 - частота интервала, следующего за модальным  19814,457 (тыс. руб.)Наиболее точным показателем асимметрии является моментный коэффициент асимметрии (As):   - центральный момент l-ого порядка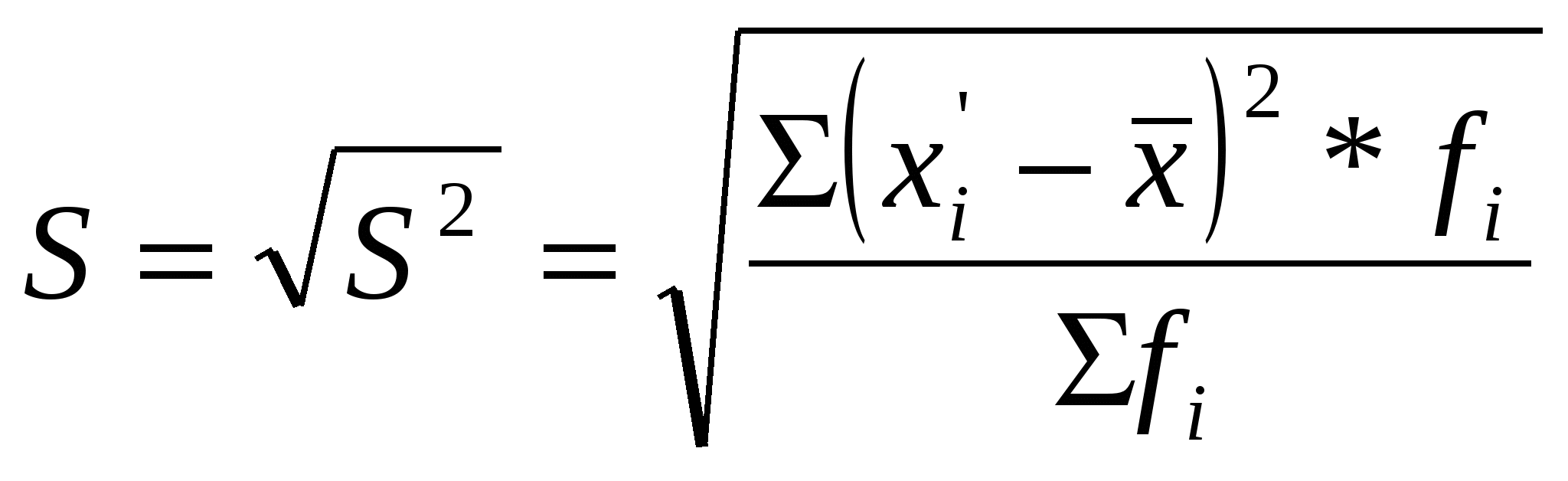 - среднее квадратическое отклонениеРасчет центральных моментов осуществлен в таблице 5. Таблица 5
S=  =20822,393S3=20822,3933=9 028 007 736 599,150 =9 895 467 547 292,160/9 028 007 736 599,150=1,096Оценка степени существенности показателя асимметрии дается с помощью средней квадратической ошибки,(SAs):  0,405 =1,096/0,405=2,705s=2,705<3, следовательно, асимметрия в рассматриваемом ряду является несущественной, и ее наличие объясняется влиянием случайных обстоятельств. Положительная величина показателя асимметрии (As=1,096>0) указывает на наличие правосторонней асимметрии. Наличие правосторонней асимметрии так же подтверждается соотношением Мо<Ме<:Мо=19814,457<Ме=26677,060< =32359,000Применяются так же структурные показатели ( коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения (т.е. основной массы единиц, и не зависящие от крайних значений признака). Рассчитаем структурный коэффициент асимметрии Пирсона (AsП) по формуле:  = (32359,000-19814,457)/20822,393=0,602AsП=0,602>0, что подтверждает вывод о правосторонней асимметрии, сделанные выше. Эксцесс определяется только для симметричных и умеренно асимметричных распределений. Эксцесс (Ex) оценивается с помощью показателя, рассчитываемого по формуле:  Расчет центрального момента 4-ого порядка осуществлен в таблице 5 S4=20822,3934=187 984 725 879 707 000,000 Ex=562 726 159 074 796 000,000/187 984 725 879 707 000,000-3=-0,007 Ex=-0.007<0 распределение является более плосковершинным по сравнению с нормальным распределением Чтобы оценить существенность эксцесса рассчитывают статистику:    0,700=0,007/0,700=0,01Отношение =0,01<3, следовательно, отклонение от нормального распределения является несущественным.Таким образом, анализируемое распределение характеризуется незначительной правосторонней асимметрией, и является более плосковершинным по сравнению с нормальным распределением. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||