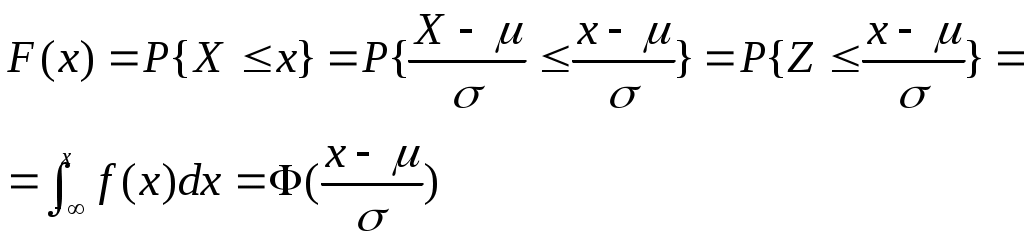|
|
как находится доверительный интервал. Как находится доверительный интервал(монте карло). Как находится доверительный интервал, внутри которого находится оценка интеграла с достаточной степенью уверенности
Как находится доверительный интервал, внутри которого находится оценка интеграла с достаточной степенью уверенности?
Выполнив 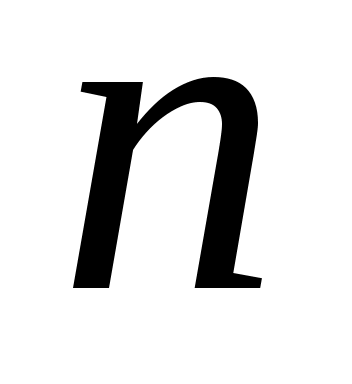 испытаний методом Монте-Карло, получаем оценку интеграла испытаний методом Монте-Карло, получаем оценку интеграла 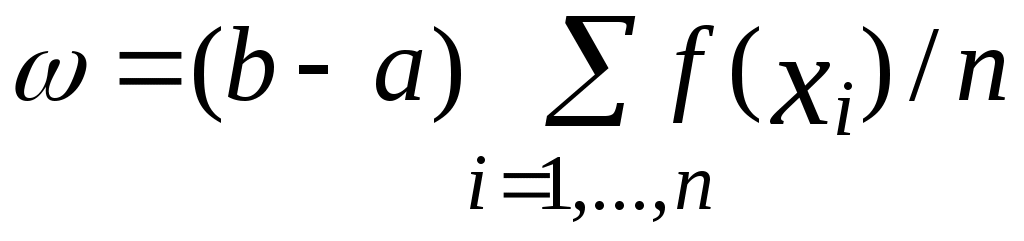 , где , где 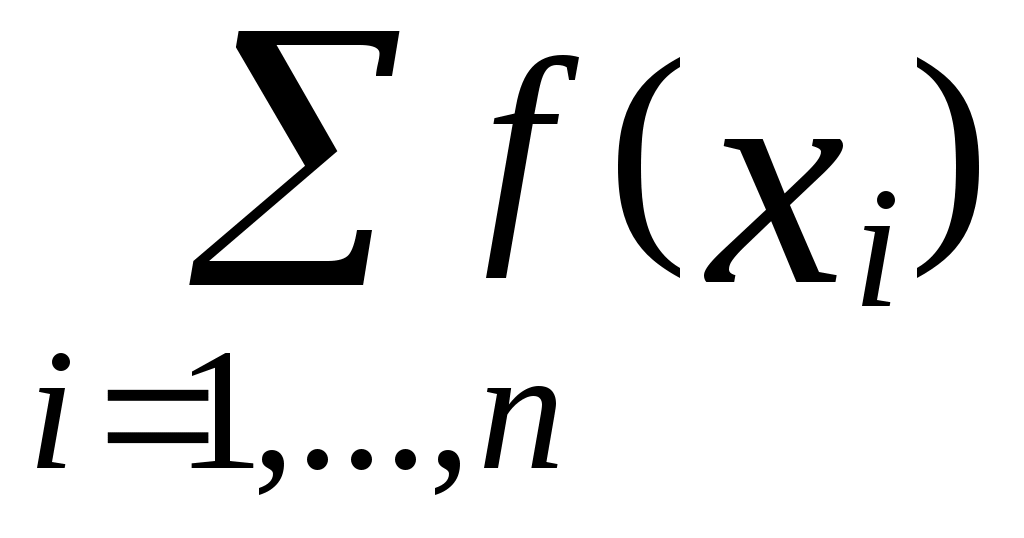 - сумма случайных переменных с одним и тем же распределением, - сумма случайных переменных с одним и тем же распределением, 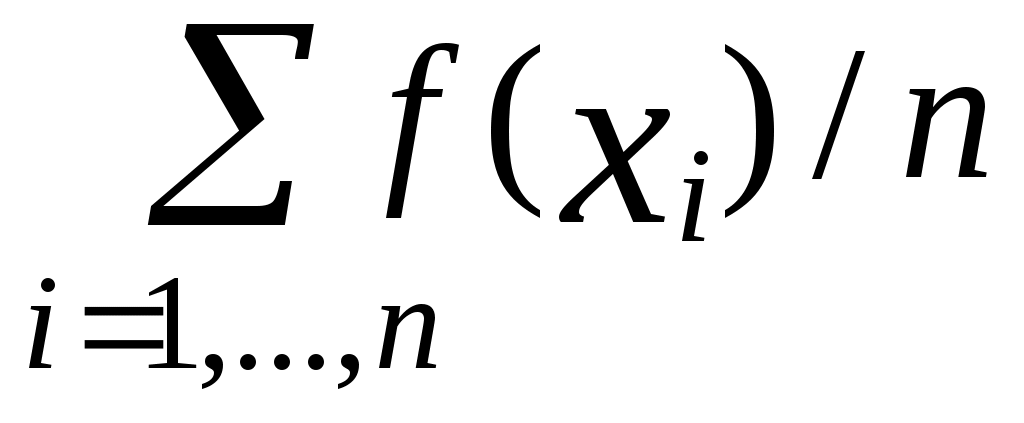 - выборочное среднее. - выборочное среднее.
Не можем точно ожидать, что выборочное среднее будет «близко» или равно 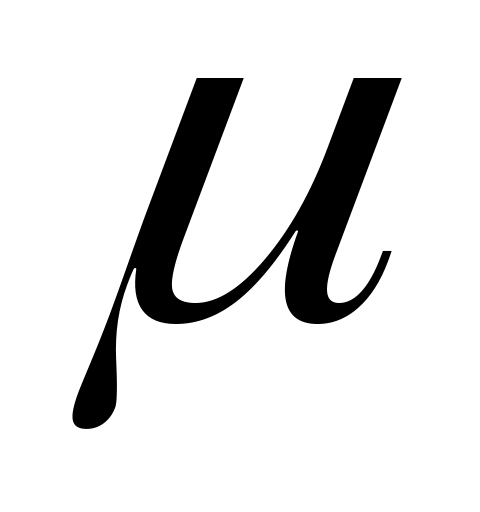 - математическому ожиданию! - математическому ожиданию!
Выход: Пусть 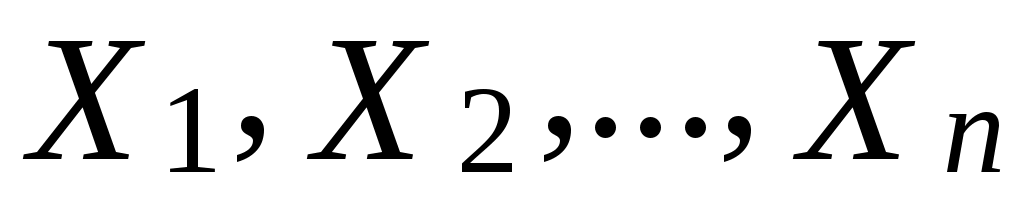 - независимые случайные переменные с одним и тем же распределением, математическим ожиданием - независимые случайные переменные с одним и тем же распределением, математическим ожиданием 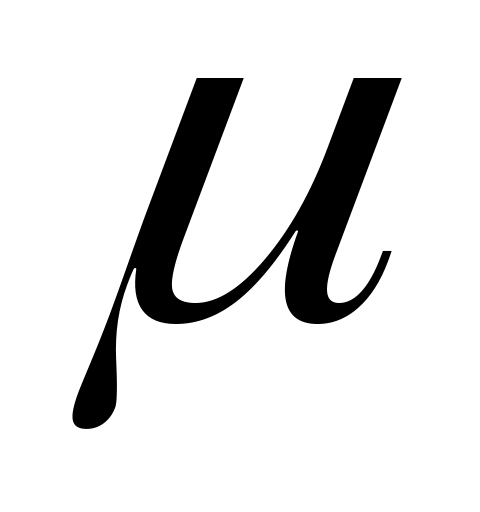 и дисперсией и дисперсией 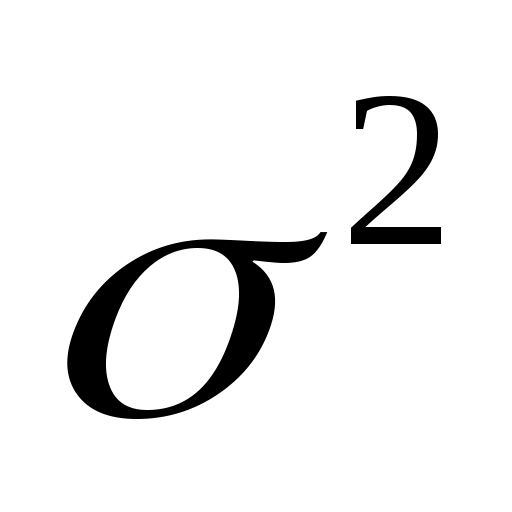 . .
Ищут доверительный интервал, внутри которого находится 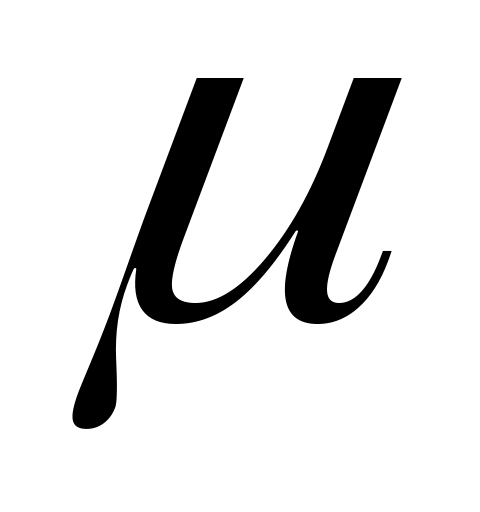 с достаточной степенью уверенности. с достаточной степенью уверенности.
Что означает «с достаточной степенью уверенности»?
Находится доверительная вероятность, которая позволяет утверждать, что выборочное среднее 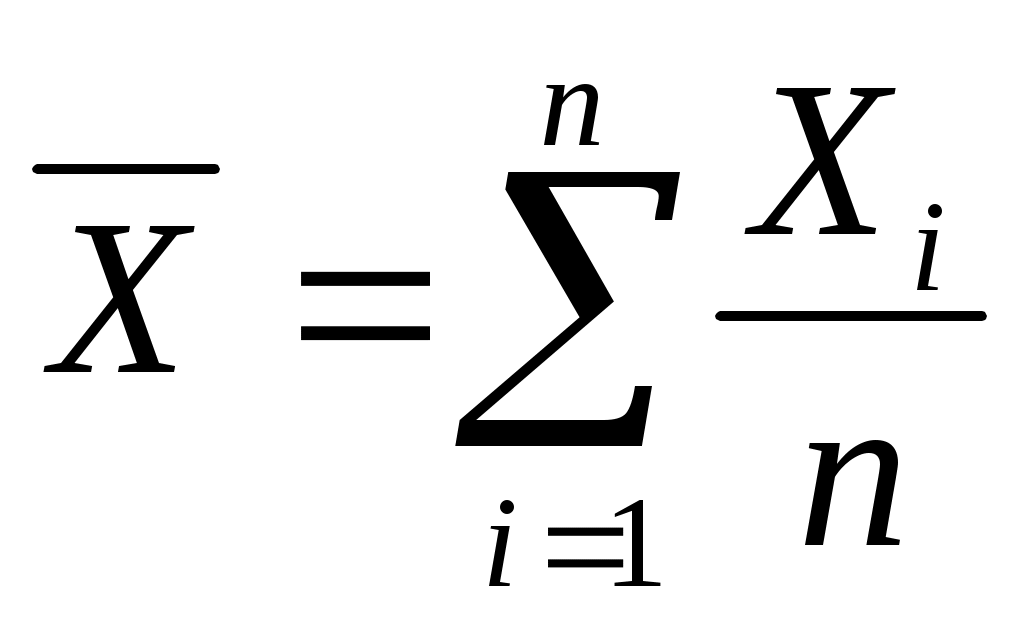 будет таковым, что математическое ожидание будет таковым, что математическое ожидание 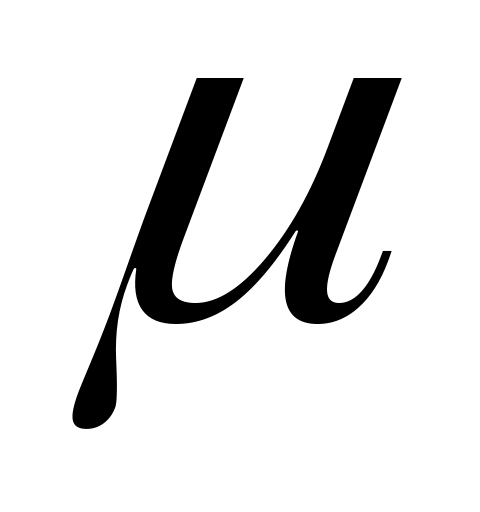 будет лежать между границами доверительного интервала. будет лежать между границами доверительного интервала.
По центральной предельной теореме (ЦПР):
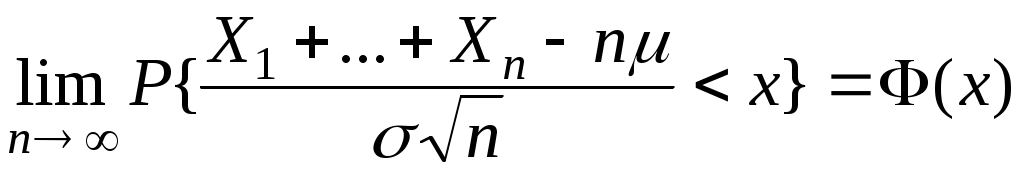 , ,
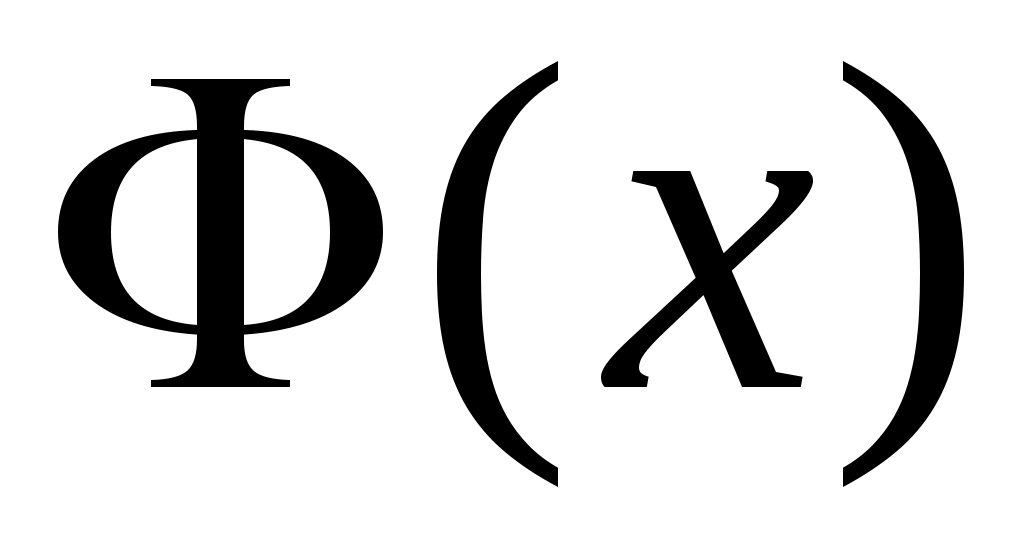 - функция распределения стандартной нормально распределенной случайной переменной с математическим ожиданием - функция распределения стандартной нормально распределенной случайной переменной с математическим ожиданием 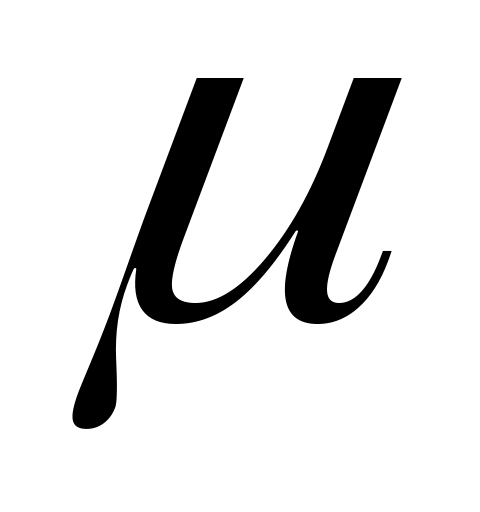 =0 и дисперсией =0 и дисперсией 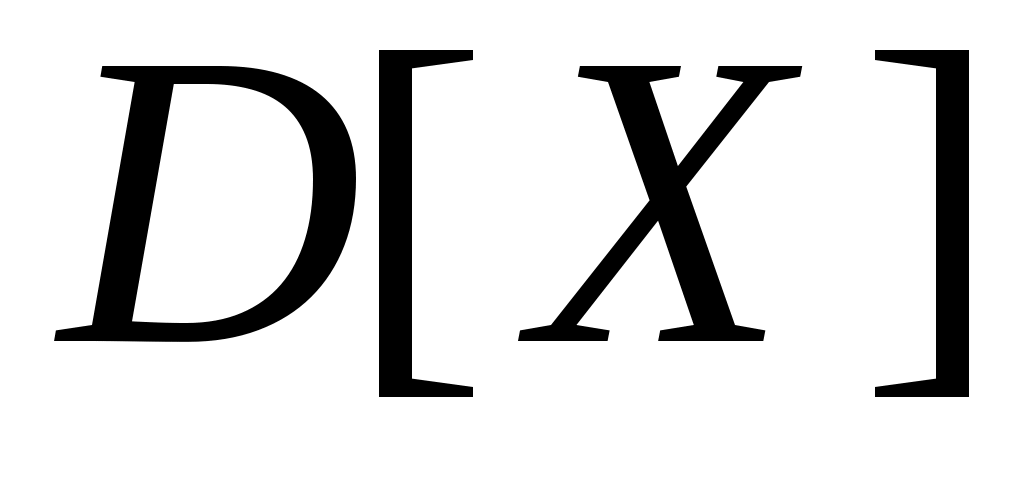 =1: =1:
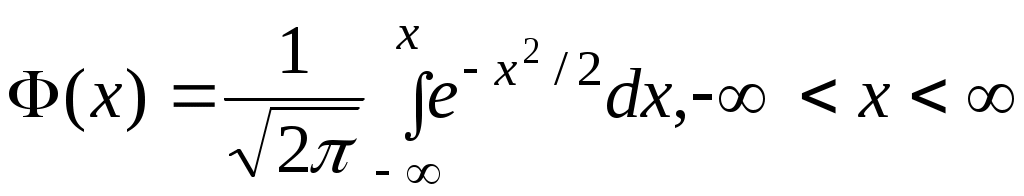
(Значение 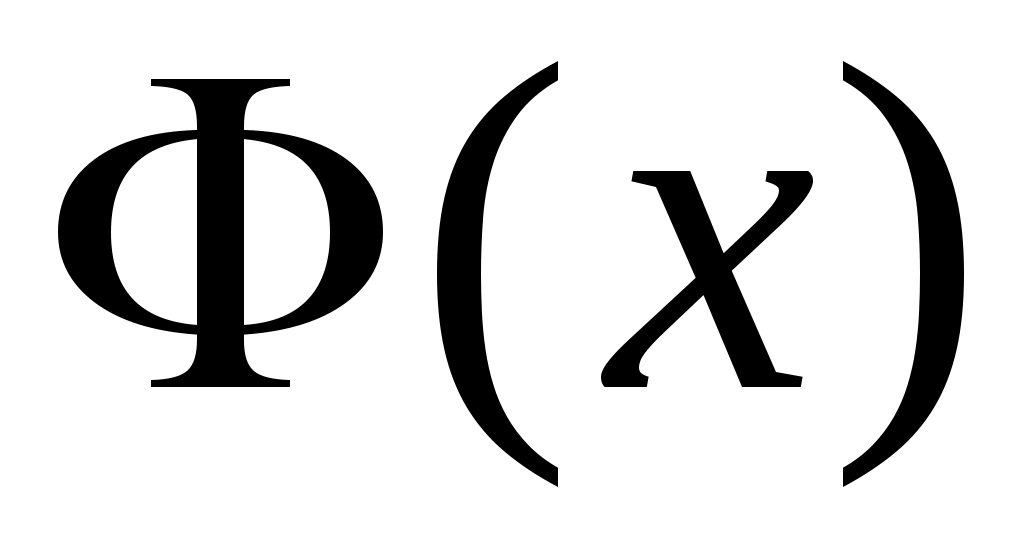 может быть вычислено с помощью специальной таблицы (есть в книге по теории вероятностей)). может быть вычислено с помощью специальной таблицы (есть в книге по теории вероятностей)).
Плотность стандартной нормально распределенной случайной переменной
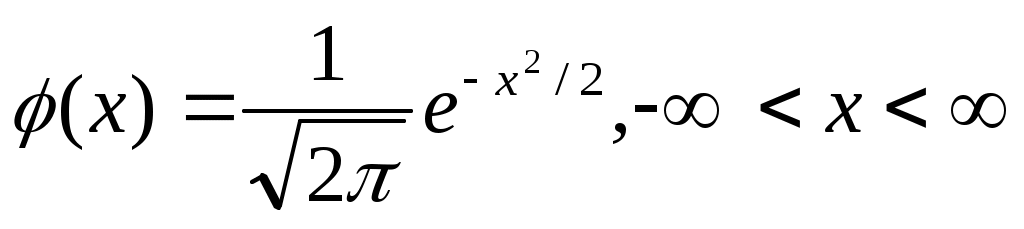
По ЦПТ: сумма большого числа независимых случайных переменных имеет приблизительно нормальное распределение и 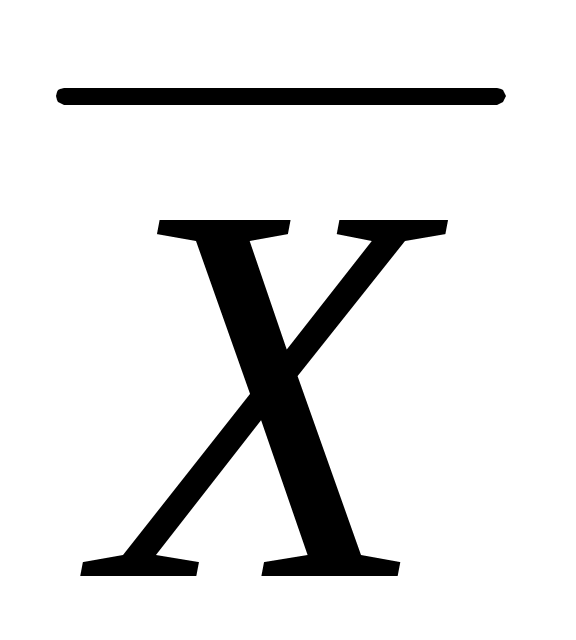 имеет приблизительно нормальное распределение. имеет приблизительно нормальное распределение.
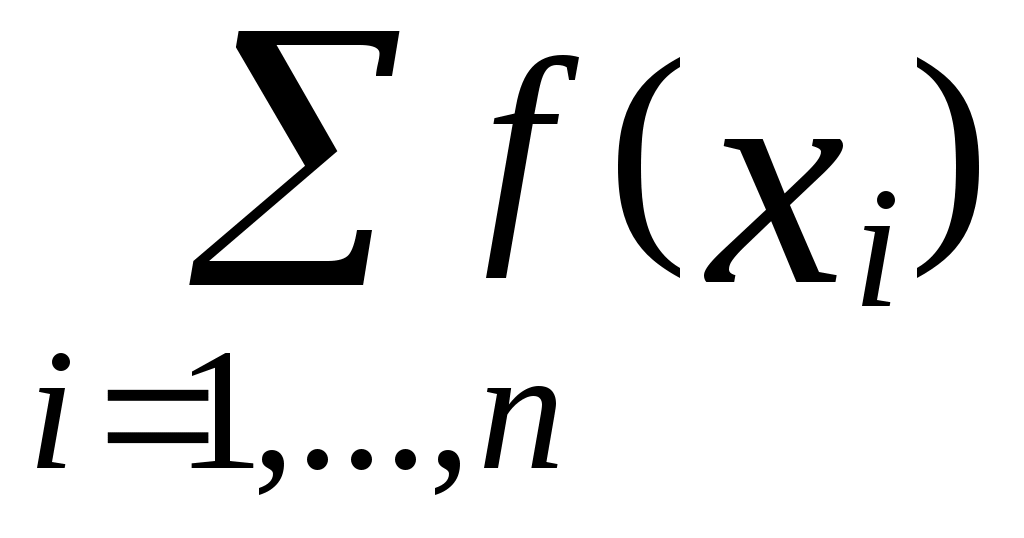 и выборочное среднее и выборочное среднее 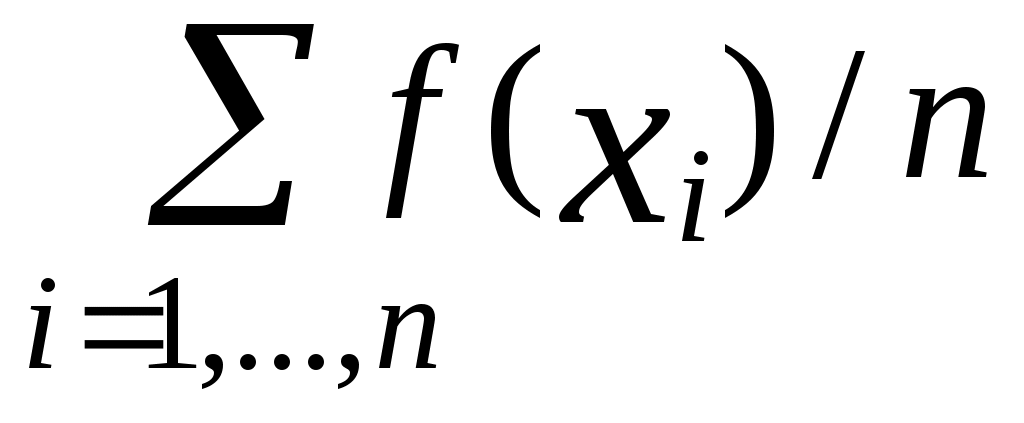 - имеет нормальное распределение по ЦПТ - имеет нормальное распределение по ЦПТ
Если 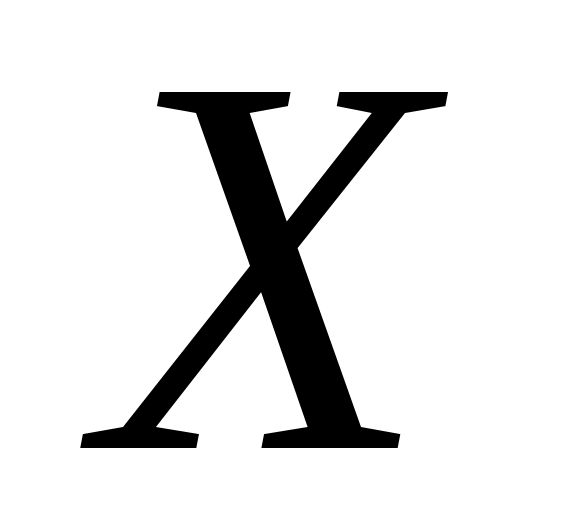 - нормально распределенная случайная переменная - нормально распределенная случайная переменная 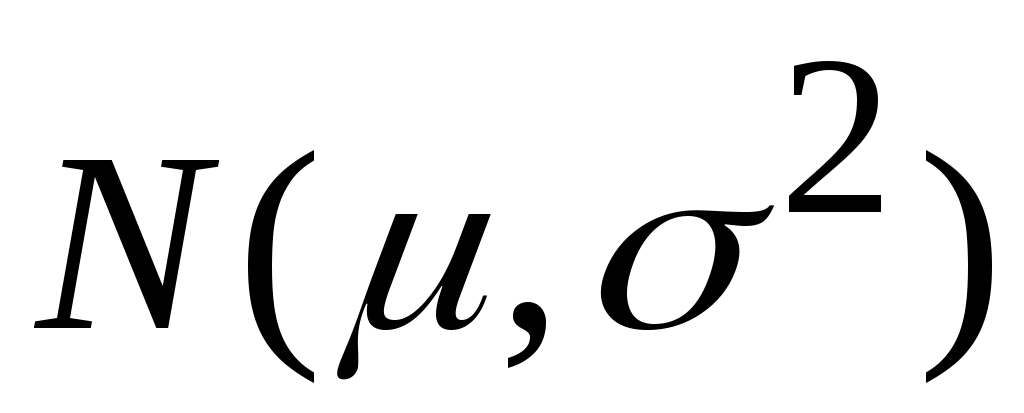 , ее плотность распределения равна: , ее плотность распределения равна:
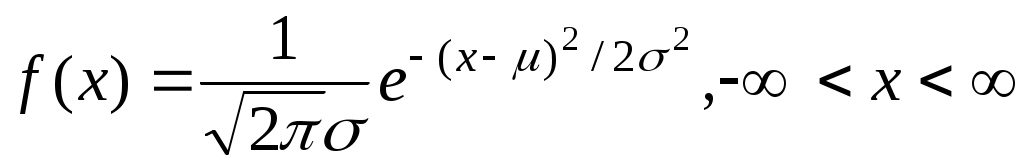
Функция распределения равна 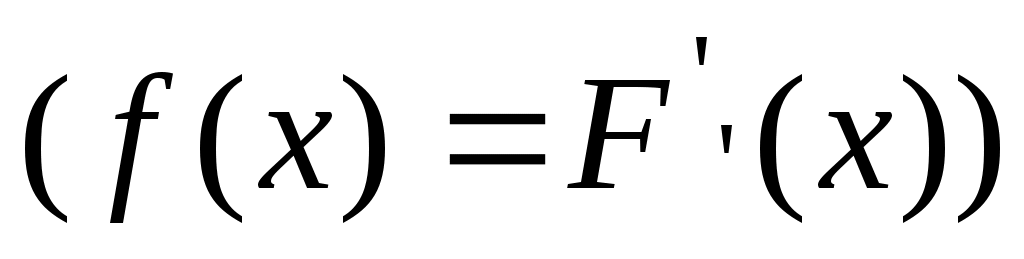 : :
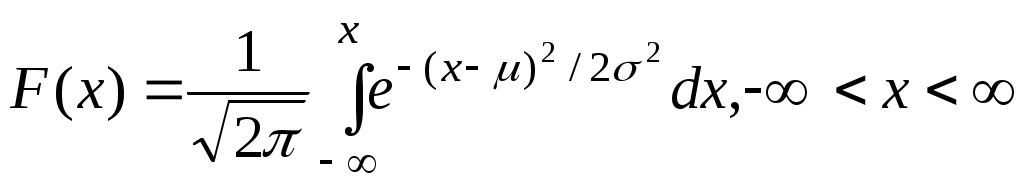
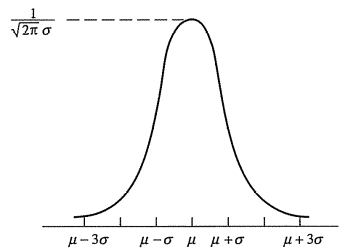
Нормальная функция плотности распределения вероятностей
Как найти доверительную вероятность?
Все вероятности, касающиеся 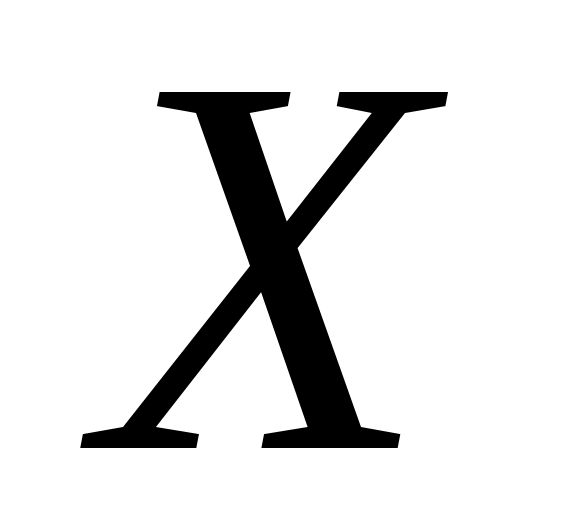 , могут быть вычислены с помощью , могут быть вычислены с помощью 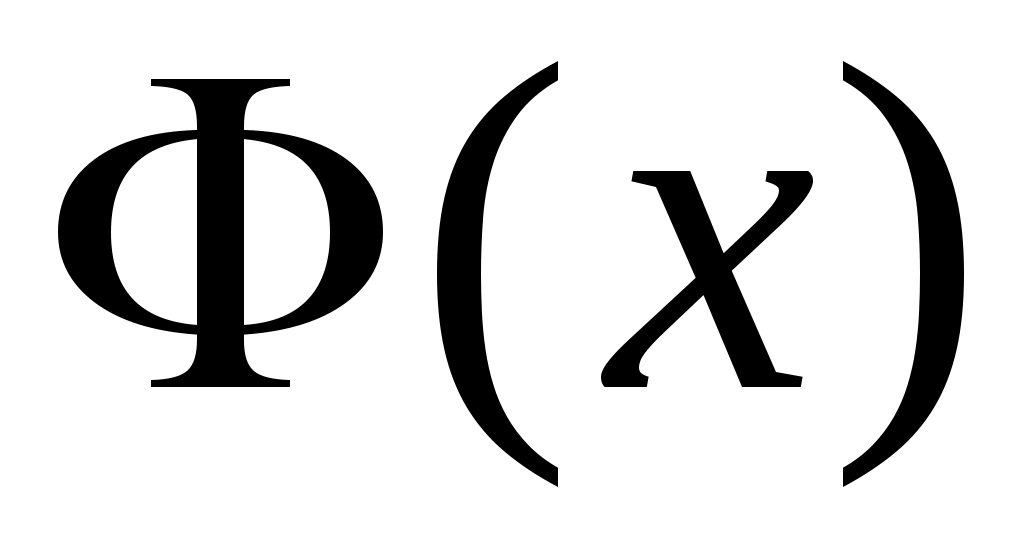 . .
Теорема: Если 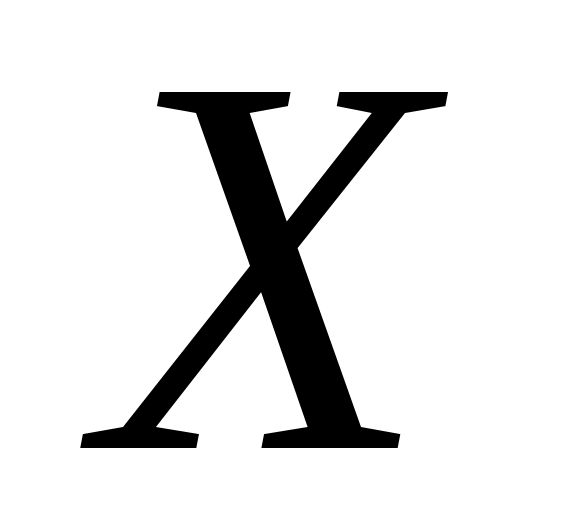 - непрерывная случайная переменная, то вероятность того, что - непрерывная случайная переменная, то вероятность того, что 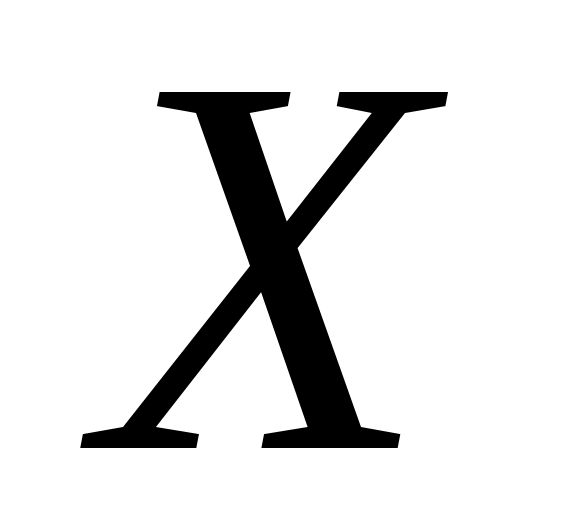 примет значение, принадлежащее интервалу примет значение, принадлежащее интервалу 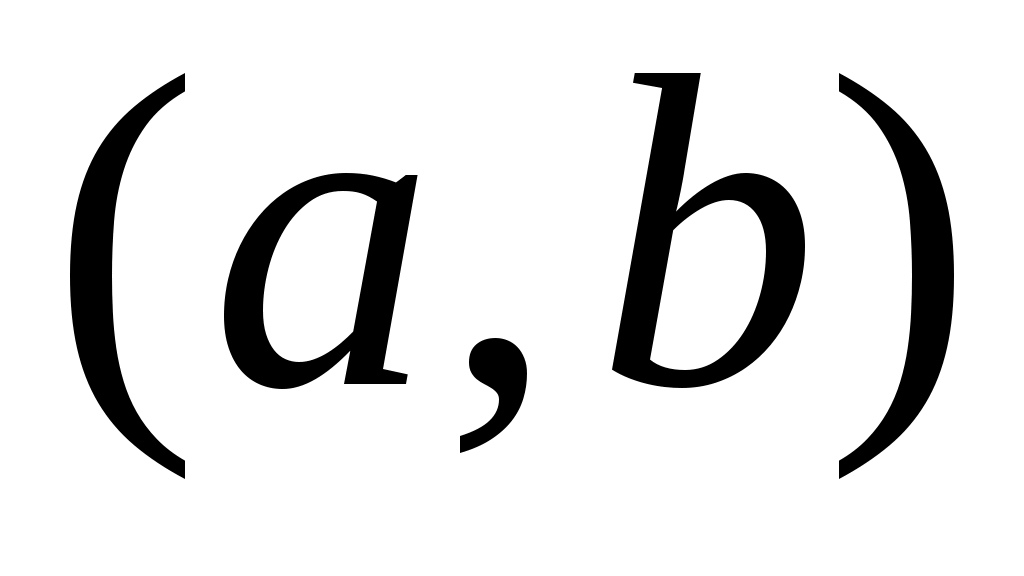 : :
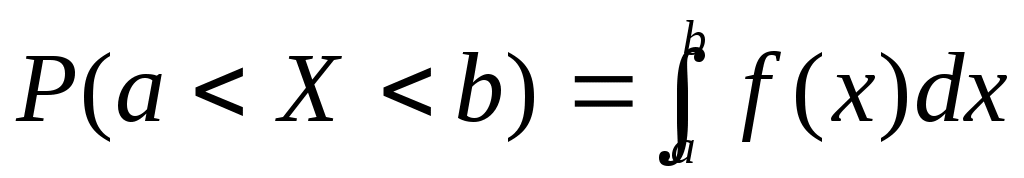 , , 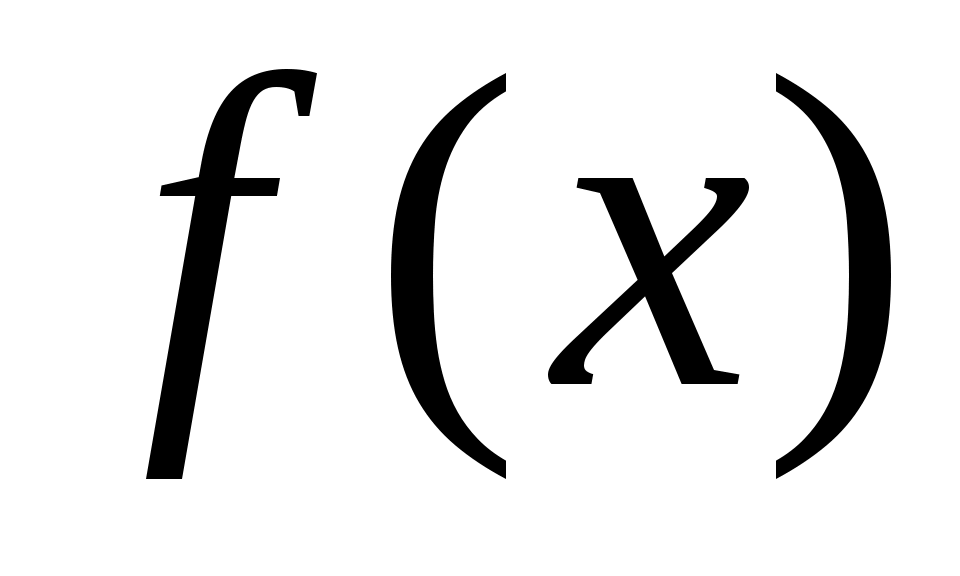 - плотность распределения. - плотность распределения.
Выразим функцию распределения 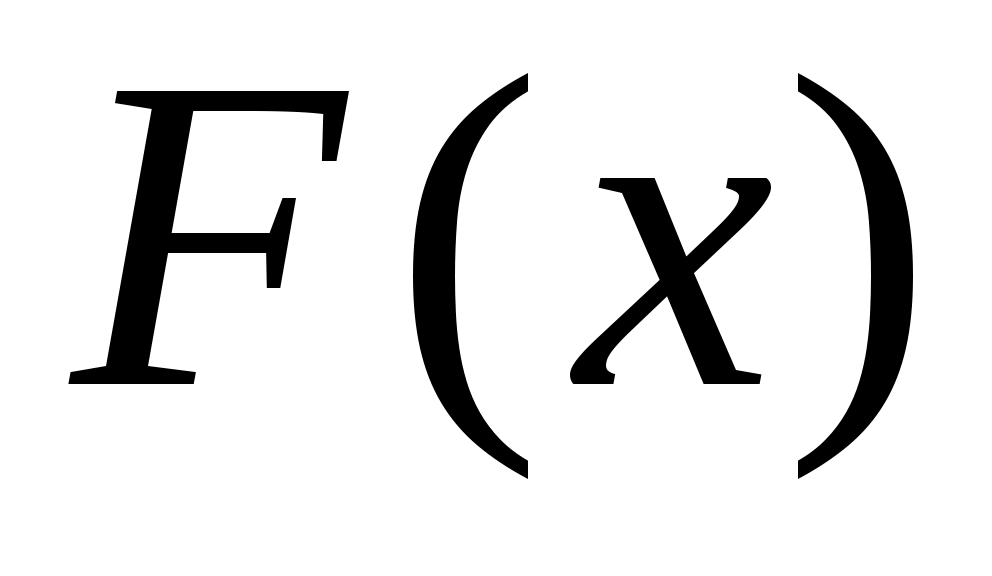 случайной переменной случайной переменной 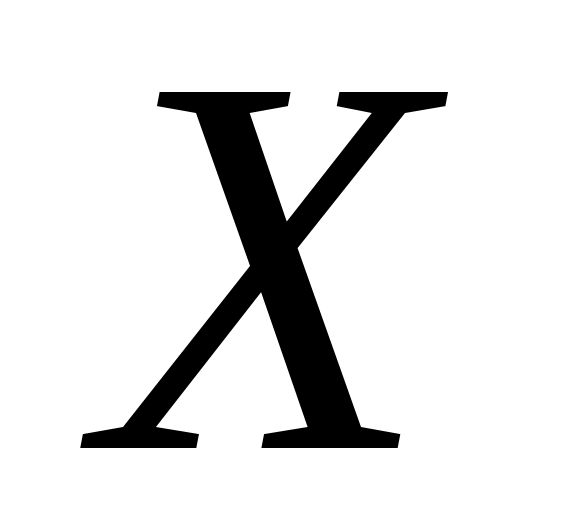 через через 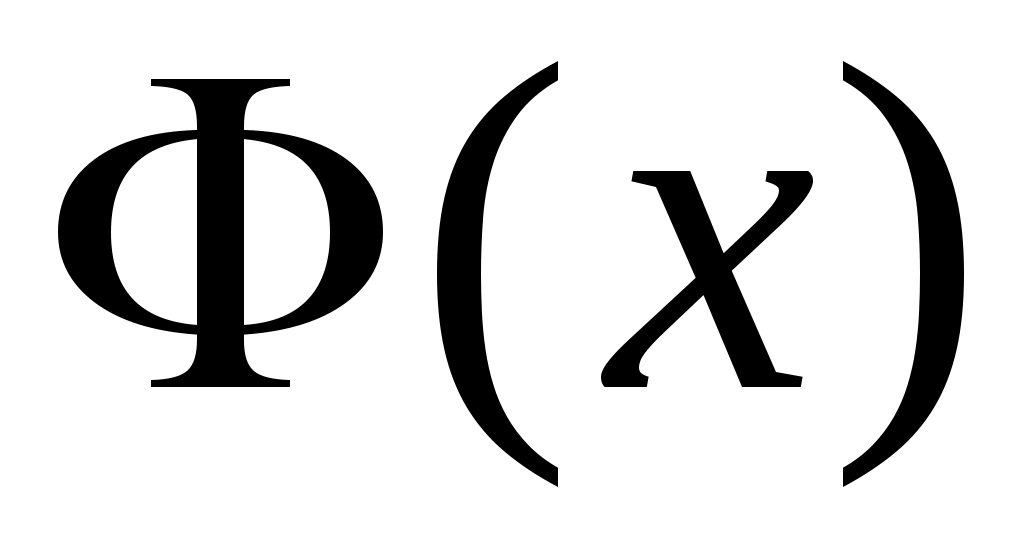 : :
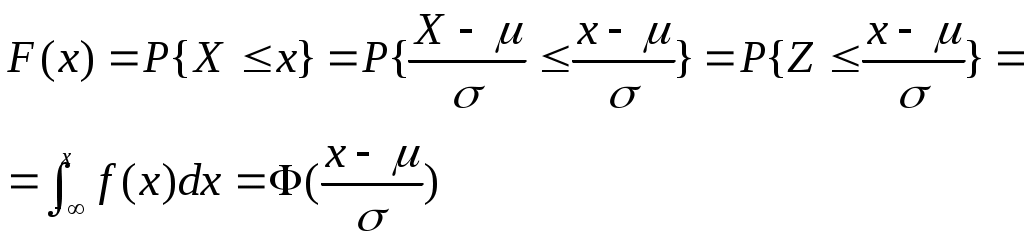
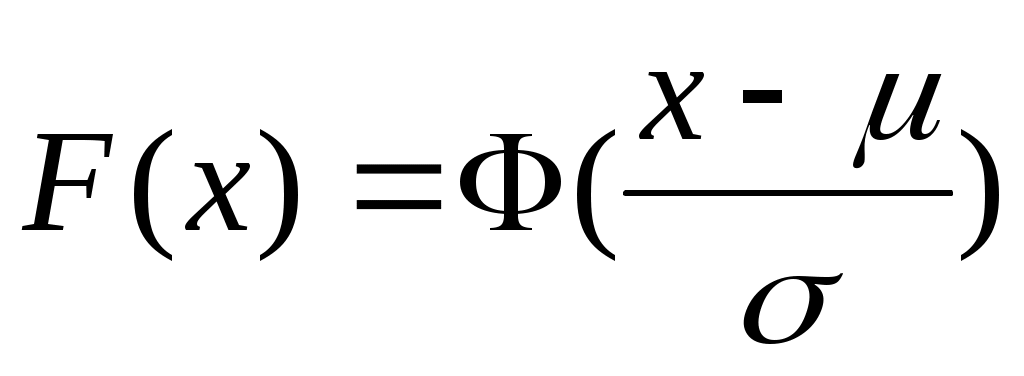
Для любого 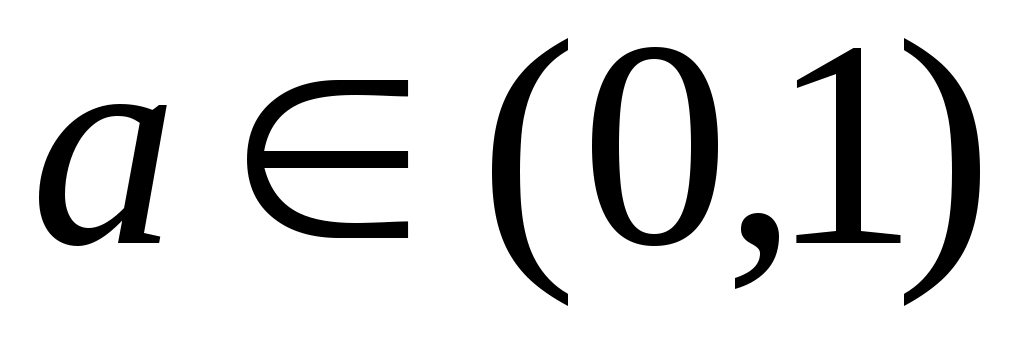 пусть пусть 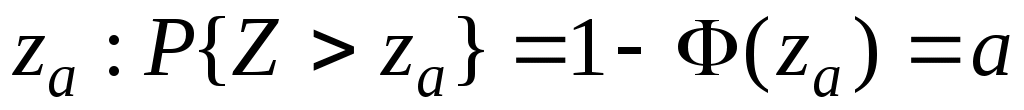 (см. рис.1). (см. рис.1).
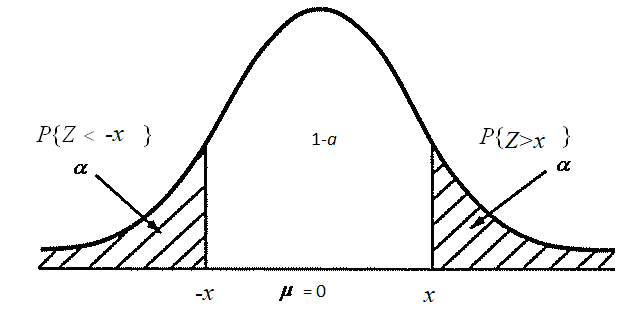
Плотность стандартного нормального распределения
Рис.1.
|
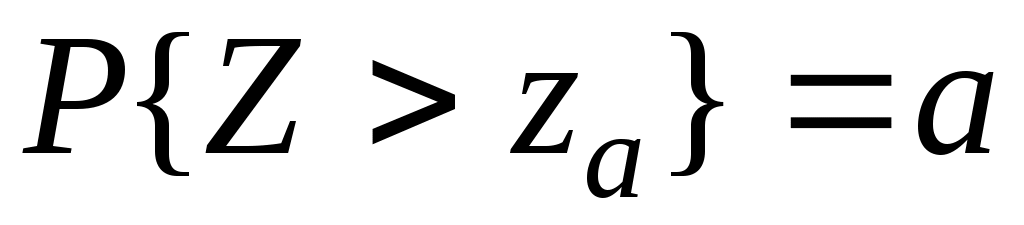
|
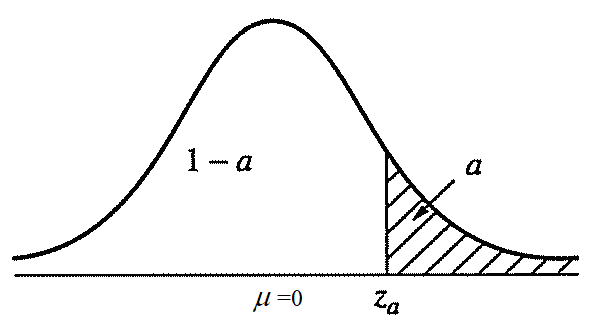
Задавая определенную доверительную вероятность 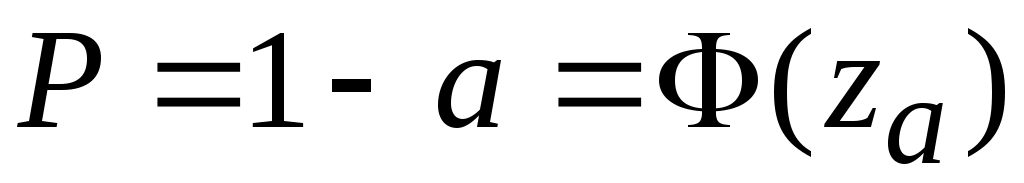 , где , где  - это уровень значимости, значение - это уровень значимости, значение 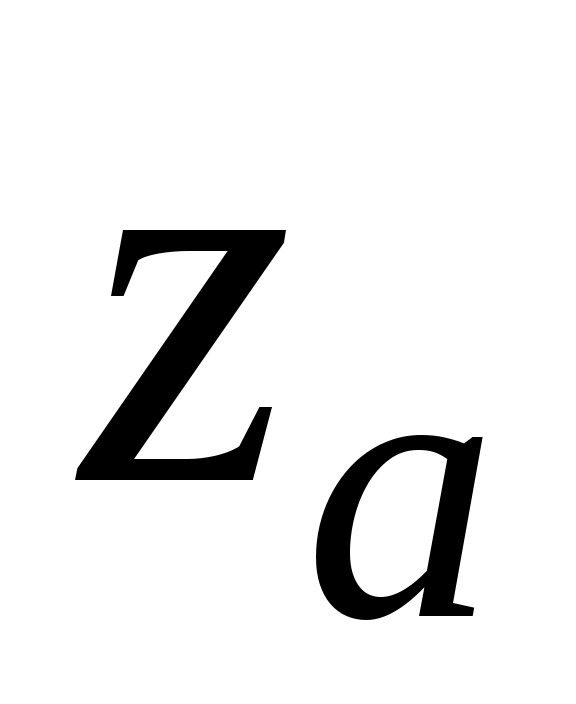 может быть получено из таблицы значений может быть получено из таблицы значений 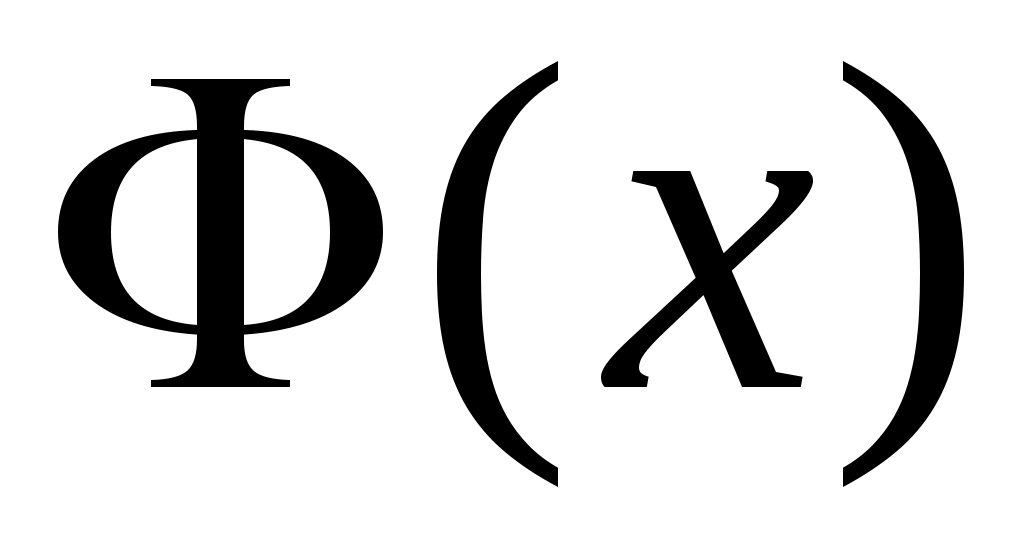 . .
Пример. 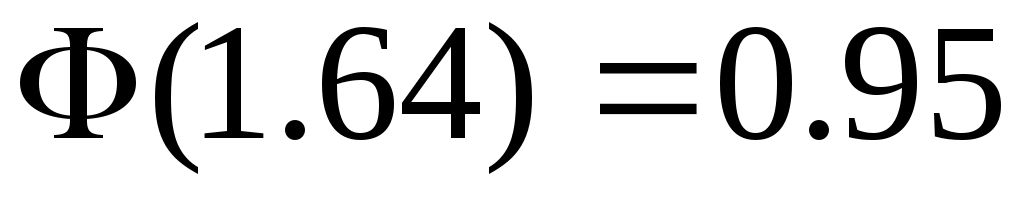 , , 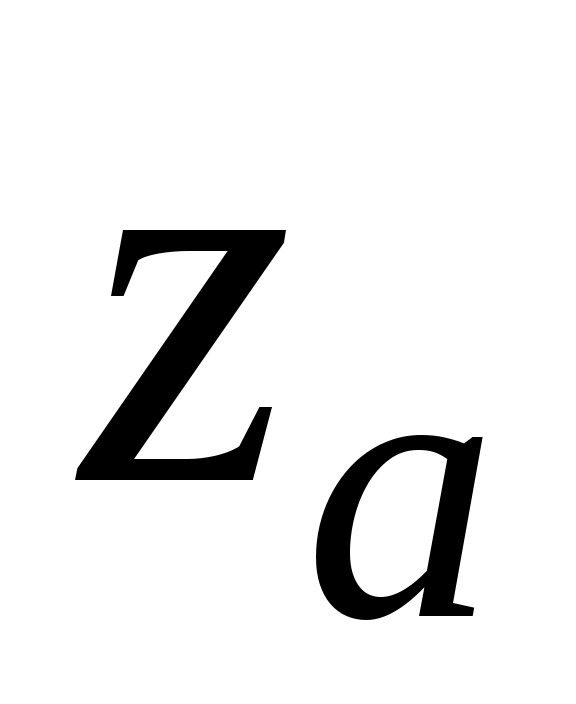 =1.64, т.е. =1.64, т.е. 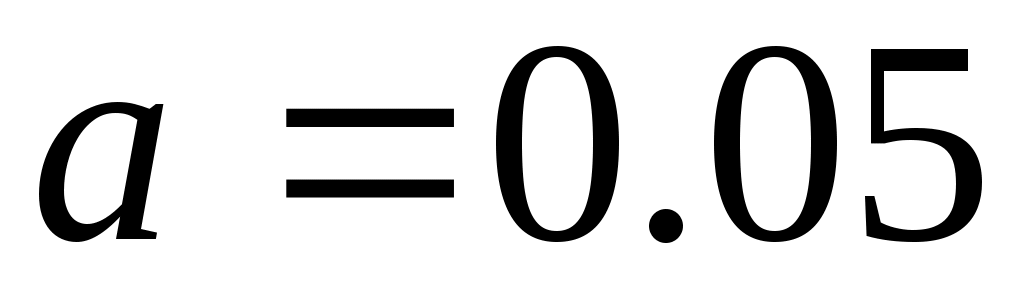 и и 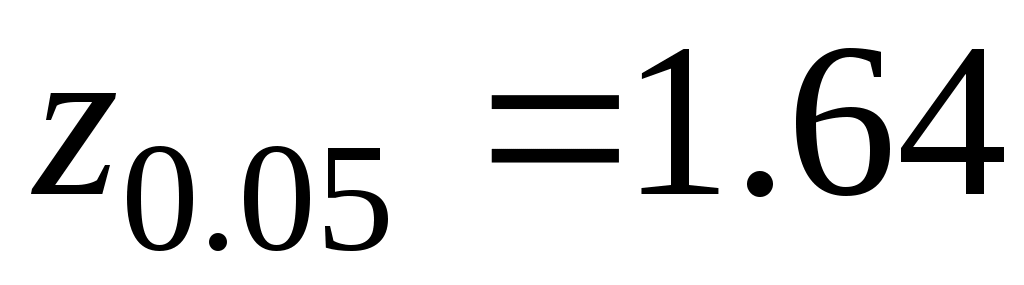
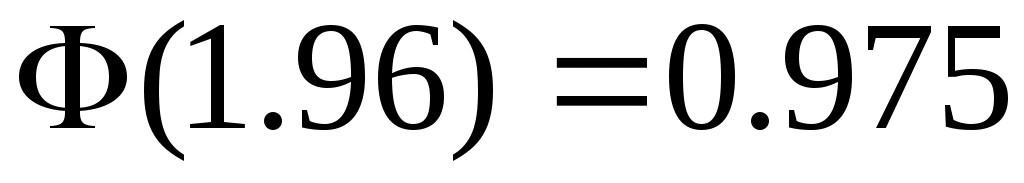 , , 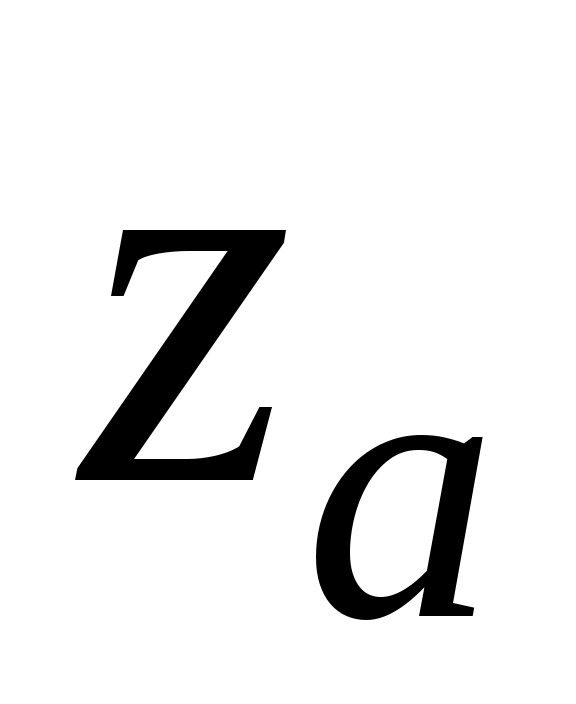 =1.96, т.е. =1.96, т.е. 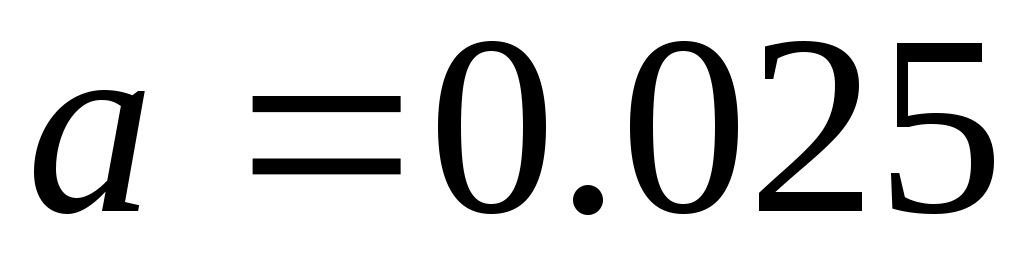 и и 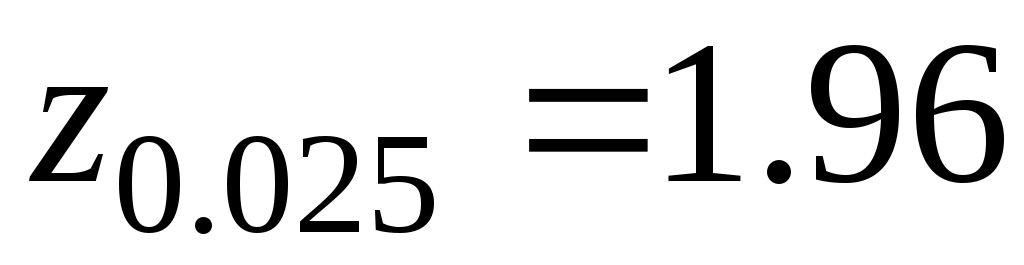
Нахождение доверительного интервала
Из ЦПТ следует:
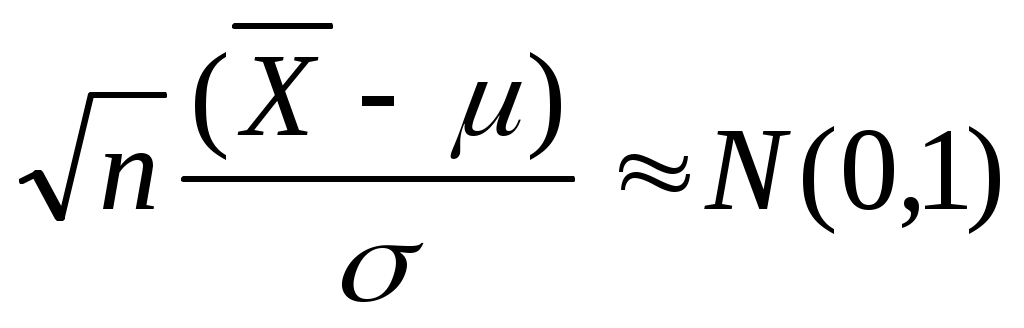 . .
Если заменить неизвестное стандартное отклонение  на его оценку на его оценку 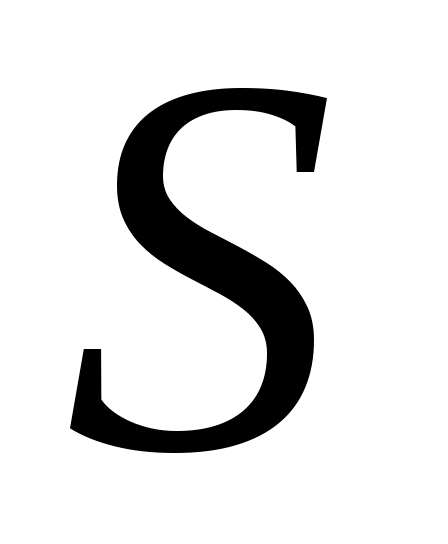 , то для больших , то для больших 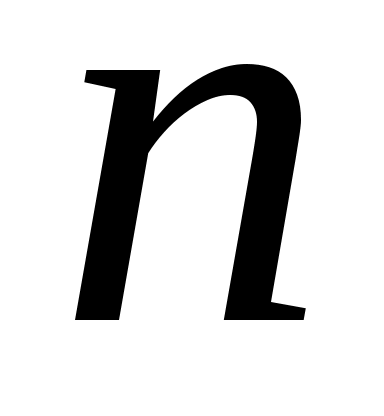
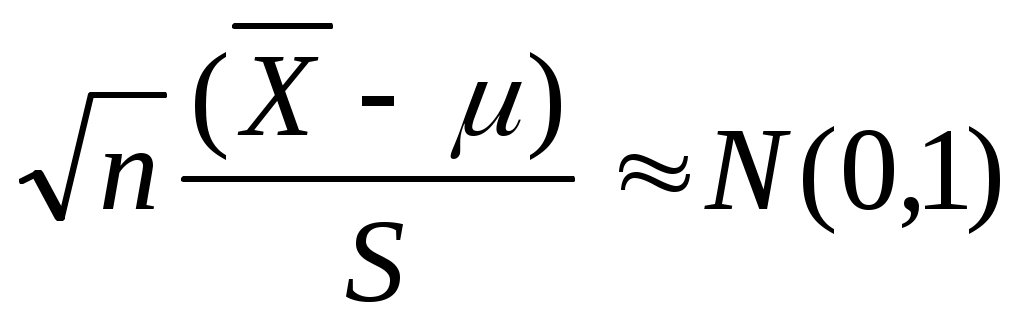 . .
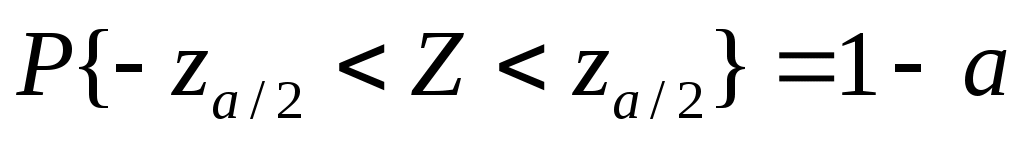 (рис.1 и 2). (рис.1 и 2).
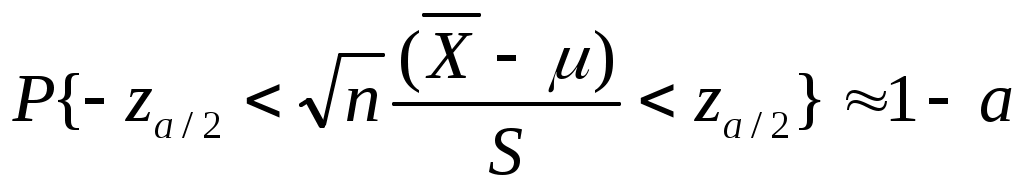 . .
Таким образом, с доверительной вероятностью 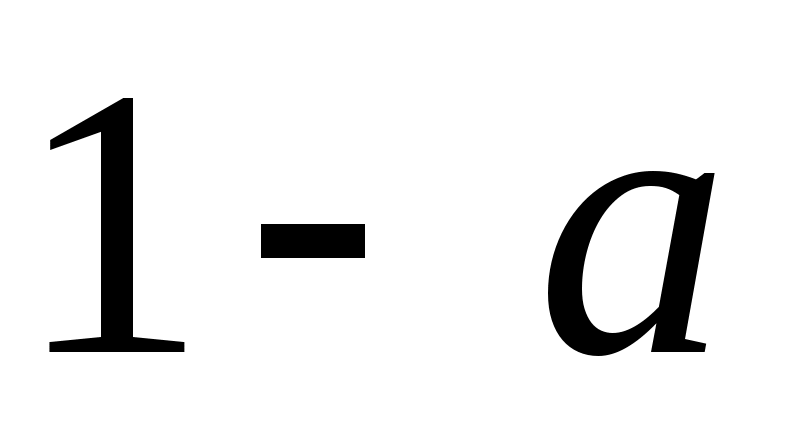 математическое ожидание математическое ожидание 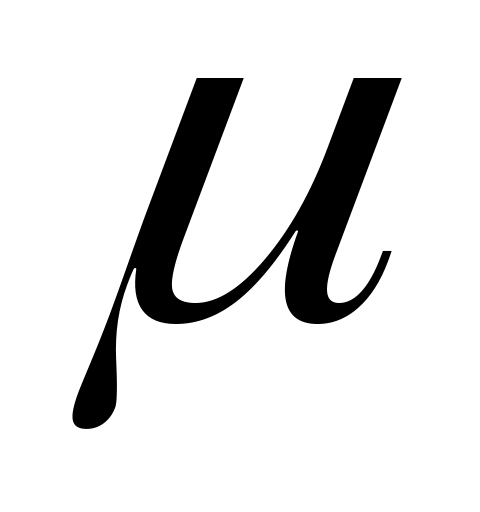 будет лежать в интервале будет лежать в интервале
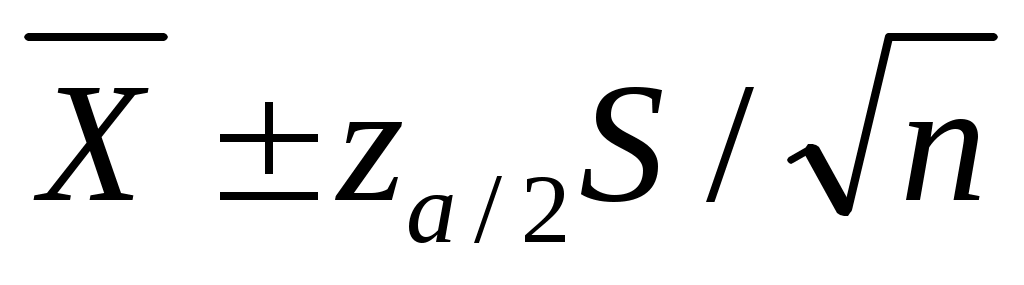 . .
Определение. Если наблюдаемые значения выборочного среднего и выборочного стандартного отклонения являются 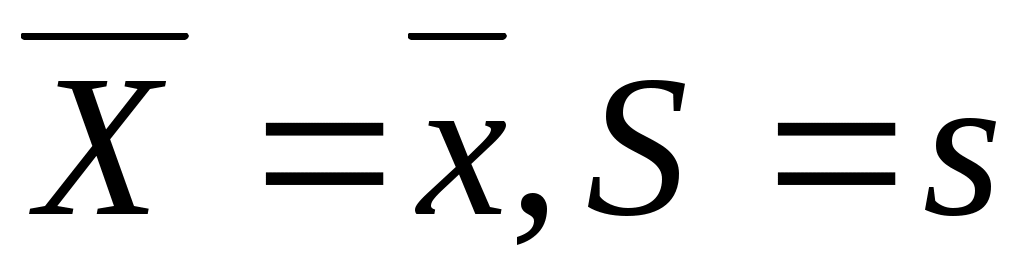 , то интервал , то интервал 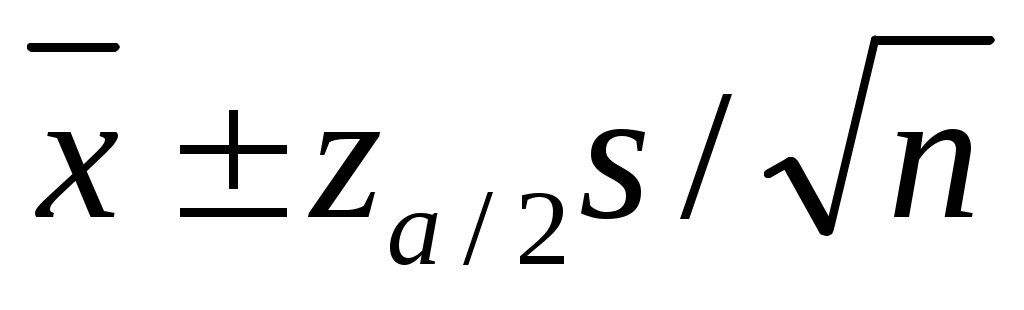 называется называется 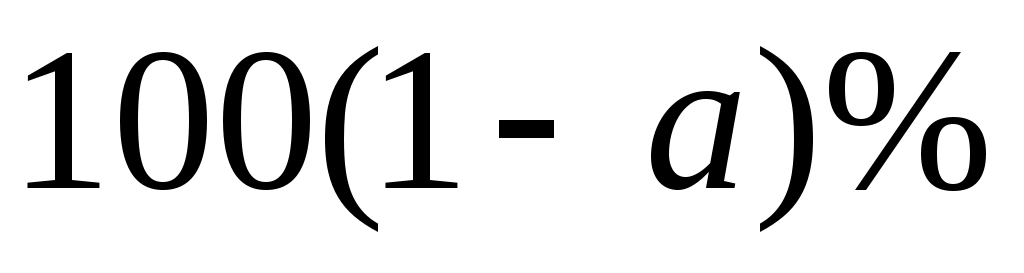 доверительным интервалом оценки доверительным интервалом оценки 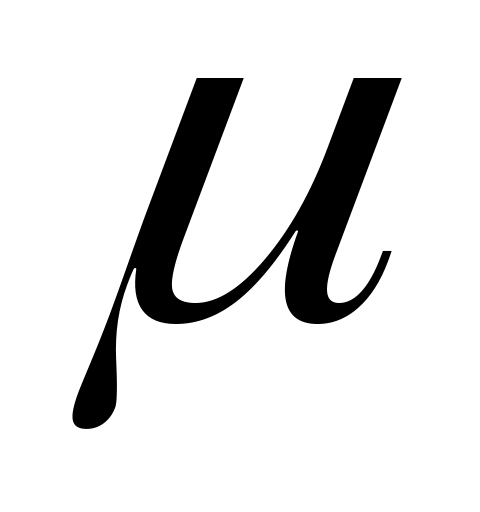 . .
Замечание. «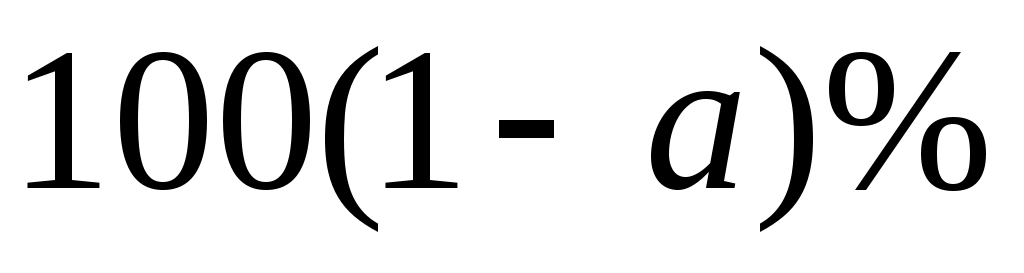 доверительный интервал» означает следующее. Пусть доверительный интервал» означает следующее. Пусть 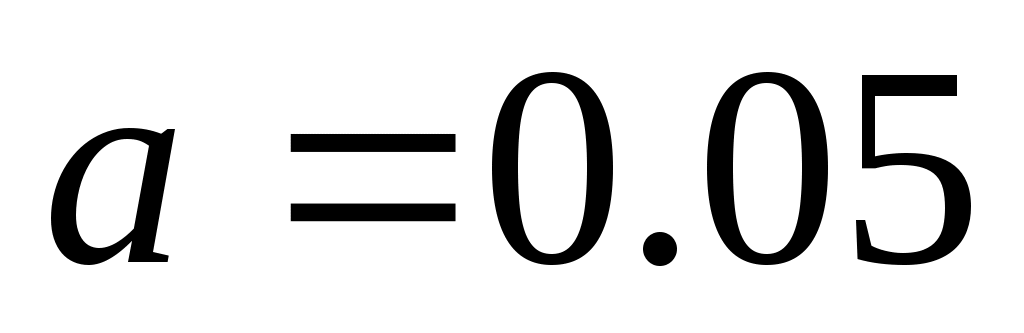 , тогда , тогда 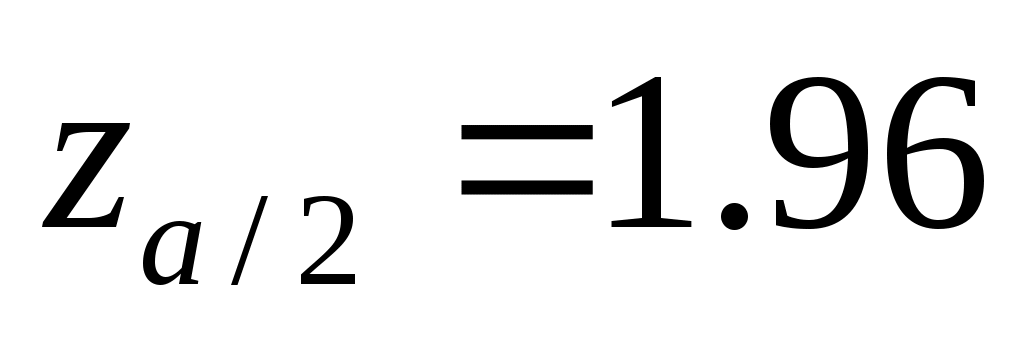 . Имея наблюдаемые значения, с доверительной вероятностью 0.95 выборочное среднее . Имея наблюдаемые значения, с доверительной вероятностью 0.95 выборочное среднее 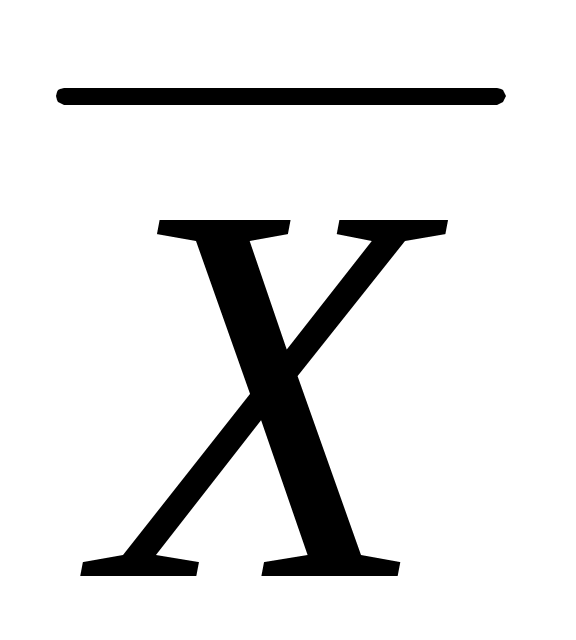 и выборочное стандартное отклонение и выборочное стандартное отклонение 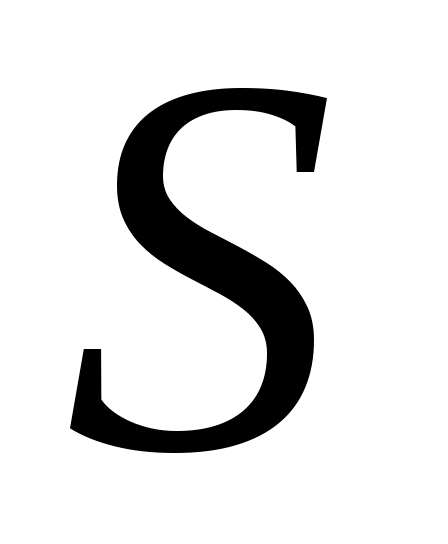 будут таковыми, что будут таковыми, что 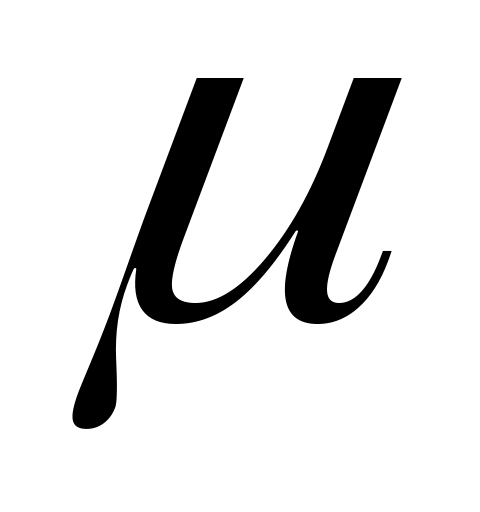 будет лежать между значениями будет лежать между значениями 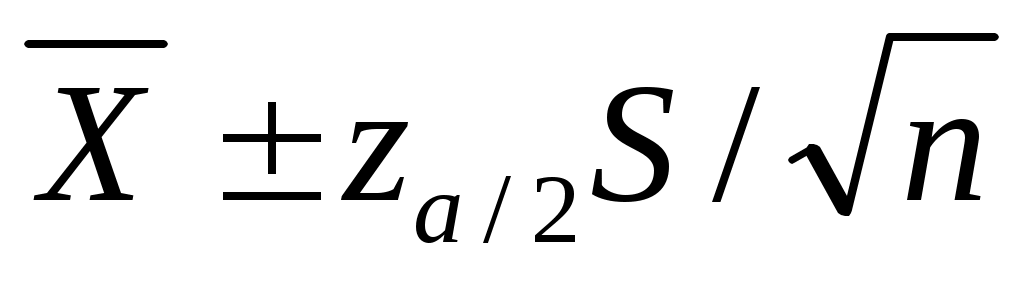 . .
|
|
|
 Скачать 1.3 Mb.
Скачать 1.3 Mb.