Радиостанция. Как переводить из десятичной системы счисления в двоичную. Как переводить из десятичной системы счисления в двоичную
 Скачать 5.23 Mb. Скачать 5.23 Mb.
|
|
Как переводить из десятичной системы счисления в двоичную Десятичная (основанная на десяти) система счисления имеет 10 возможных значений (0,1,2,3,4,5,6,7,8 или 9) для каждого поместного значения. Двоичная система счисления (основанная на двух), в свою очередь, имеет два возможных значения каждого поместного значения – 0 или 1.[1] Так как двоичная система является внутренним языком компьютеров, то серьезные программисты должны понимать, как переводить из десятичной системы счисления в двоичную, о чем вам и расскажет данная статья.  1. Поставьте задачу. Для этого примера давайте переведем десятичное число 15610 в двоичную систему. Запишите десятичный номер как делимое в «делении столбиком» (справа), затем запишите основание «2» как делитель, то есть слева от знака деления. Этот метод гораздо проще понять, когда вы видите все вычисления на бумаге. Кроме того, этот метод, основанный на делении на 2, еще и довольно прост для понимания начинающих. Чтобы не путать числа до и после перевода, стоит записывать основание системы, в которой вы работаете, рядом с каждым соответствующим числом. Тогда десятичные числа будут записываться с базовым индексом 10, а двоичные – с базовым индексом 2, соответственно.  2. Выполните действие деления. Запишите целый ответ (частное) под знаком деления, а остаток (0 или 1) запишите справа от делимого.[2] Так как мы сейчас делим на 2, то, когда делимое четное, двоичный остаток будет равен 0, а когда делимое нечетное, то двоичный остаток будет равен 1. 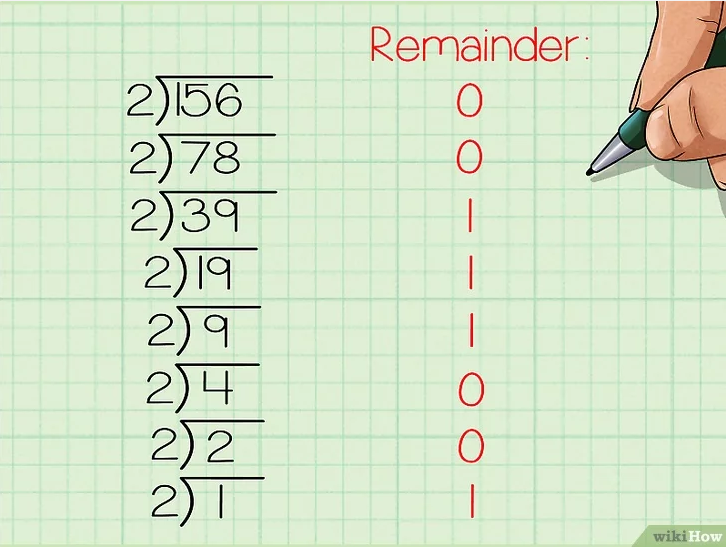 3. Продолжайте двигаться вниз, деля каждое новое частное на два и записывая остатки справа от каждого делимого. Остановитесь, когда частное будет равно 0.  4. Запишите новое, бинарное число. Прочитайте последовательность остатков снизу вверх, начиная с последнего остатка. В нашем примере у вас должно было получиться 10011100. Это двоичный эквивалент десятичного числа 156. Это же число, записанное с базовыми индексами, выглядит так: 15610 = 100111002 Этот метод может быть изменен для переведения из десятичной в «любую» систему. Мы использовали делитель 2, так как переводили в двоичную систему. Если бы мы хотели перевести наше число в девятиричную систему, то есть в систему с основанием 9, то делили бы на девять, а не на два. В результате мы бы получили число в желаемой системе. Метод2 Метод Второй: Сравнение уменьшающихся степеней и вычитание  1. Начните с создания таблицы. Запишите значения числа 2 в той или иной степени, ведя запись справа налево. Начните с 20, дав ей значение "1". Увеличивайте показатель степени на единицу для каждой степени. Продолжайте работу над списком, пока не получите число, которое находится очень близко к тому, с которым вы работаете. Допустим, мы работаем... снова с числом 15610, переводя его из десятичной в двоичную систему счисления.  2. Вычислите самую большое значение степени, помещающееся в число, которое вы хотите перевести в двоичную систему. Какое наибольшее значение степени двойки поместится в 156? Число 128 (2 в седьмой степени) помещается, поэтому самый левый знак двоичной записи будет 1. Далее вам нужно вычесть 128 из 156, что будет равняться 28. 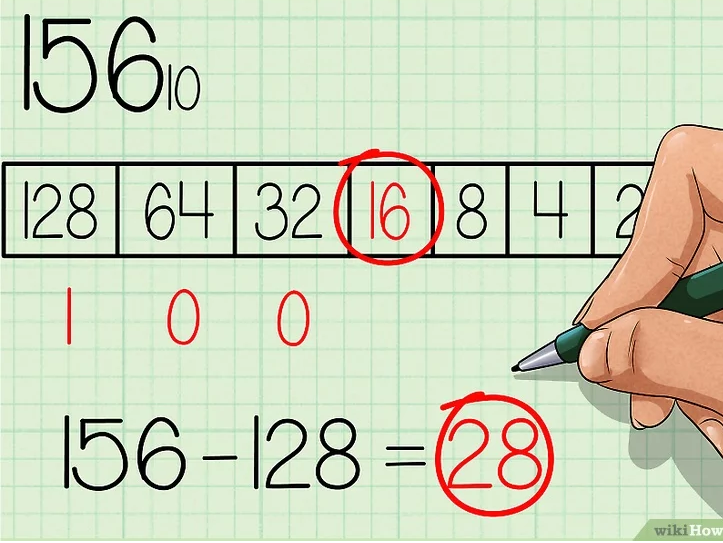 3. Переходите к следующей степени двойки. Итак, теперь мы работаем с числом 28. Давайте посмотрим по нашему списку, какая следующая степень двойки может поместиться в число 28? 64 помещается в 28? Нет, значит следующий знак в двоичной записи (справа от первого) – 0. Продолжать нужно до тех пор, пока вы не найдете число, которое все же поместится в 28. 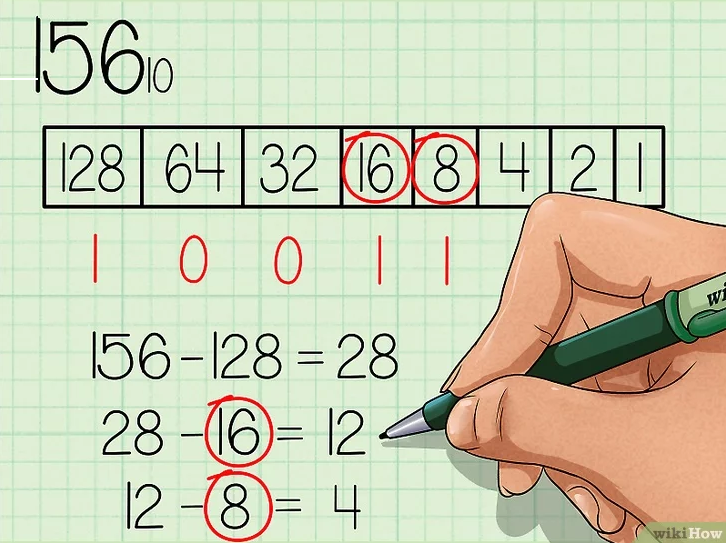 4. Вычитайте каждое следующее помещающееся число, отмечайте его цифрой "1". Итак, 16 помещается в 28, поэтому давайте запишем цифру 1 под ним и вычтем 16 из 28. Результат равен 12, а в это число помещается восьмерка. Соответственно, надо записать цифру 1 под 8, а затем вычесть 8 из 12, что будет равняться 4.  5. Продолжайте вычитать, пока не дойдете до конца таблицы. Не забывайте отмечать цифрой "1" все те числа, которые помещаются в ваше новое число, и цифрой "0" все те, которые не помещаются. 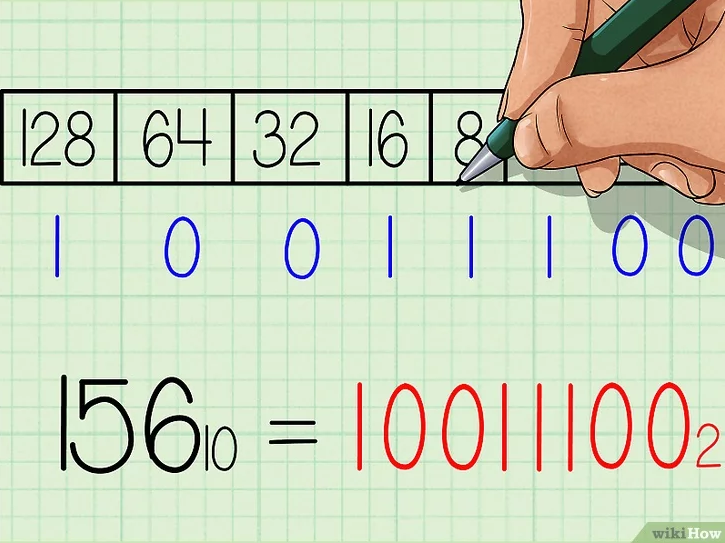 6. Запишите получившееся двоичное число. Это число будет точно таким же, какой будет последовательность нулей и единиц в нашей таблице, если читать ее слева направо. У вас должно было получиться 10011100. Это двоичный эквивалент десятичного числа 156. Или, если записывать с базовыми индексами: 15610 = 100111002. Повторяя этот метод, вы запомните степени двойки, что позволит вам пропустить первый шаг данного руководства. Как конвертировать из двоичного в десятичный Вам нужно преобразовать набор двоичных чисел (0 и 1) в десятичное значение? Существует несколько простых способов преобразования двоичных чисел, но мы сосредоточимся на самых простых и экономящих время решениях! Эта статья научит вас, как сделать преобразование двоичного кода в десятичный с использованием позиционной нотации. Как использовать позиционную нотацию  1. Запишите двоичное число и перечислите степени 2 справа налево. Допустим, мы хотим преобразовать двоичное число 10011011 2 в десятичное. Сначала запишите это. Затем запишите степени двух справа налево. Начните с 2 0, оценив его как "1". Увеличьте показатель степени на единицу для каждой степени. Остановитесь, когда количество элементов в списке равно количеству цифр в двоичном числе. Пример числа 10011011 состоит из восьми цифр, поэтому список с восемью элементами будет выглядеть следующим образом: 128, 64, 32, 16, 8, 4, 2, 1 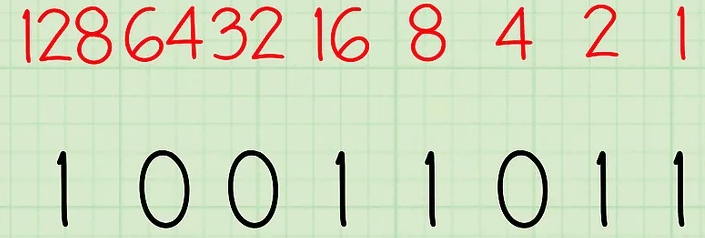 2. Запишите цифры двоичного числа ниже их соответствующих степеней двух. Теперь просто напишите 10011011 под числами 128, 64, 32, 16, 8, 4, 2, и 1 так, чтобы каждая двоичная цифра соответствовала своей степени двойки. "1" справа от двоичного числа должно соответствовать "1" справа от перечисленных степеней двух и так далее. Вы также можете написать двоичные цифры выше степеней двух, если вы предпочитаете это таким образом. Важно то, что они совпадают. 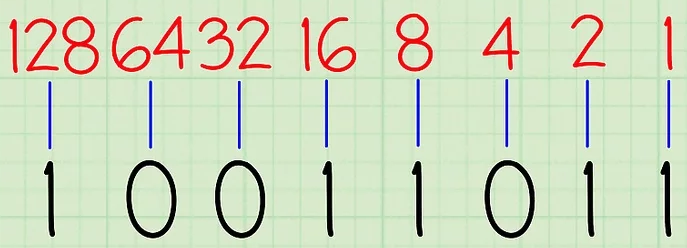 3. Соедините цифры в двоичном числе с соответствующими им степенями двух. Проведите линии, начиная справа, соединяя каждую последовательную цифру двоичного числа со степенью двух, которая находится следующей в списке над ней. Начните с рисования линии от первой цифры двоичного числа до первой степени двух в списке над ним. Затем нарисуйте линию от второй цифры двоичного числа до второй степени двух в списке. Продолжайте соединять каждую цифру с соответствующей степенью двойки. Это поможет вам визуально увидеть связь между двумя наборами чисел. 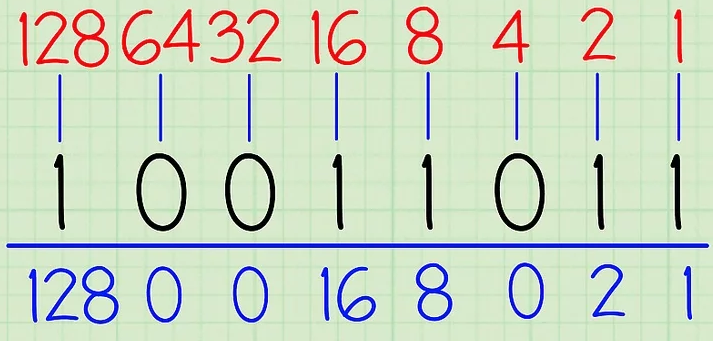 4. Запишите конечное значение каждой степени двойки. Если цифра равна 1, напишите соответствующую ей степень два ниже строки, под цифрой. Если цифра равна 0, напишите 0 под строкой, под цифрой. Поскольку "1" соответствует "1", он становится "1". Поскольку "2" соответствует "1", он становится "2". Поскольку "4" соответствует "0", он становится "0". Поскольку "8" соответствует "1", оно становится "8", а поскольку "16" соответствует "1", оно становится "16". "32" соответствует "0" и становится "0", а "64" соответствует "0" и, следовательно, становится "0".в то время как "128" соответствует "1" и становится 128.  5. Добавьте конечные значения. Теперь сложите числа, написанные под строкой. Вот что вы делаете: 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 = 155. Это десятичный эквивалент двоичного числа 10011011. 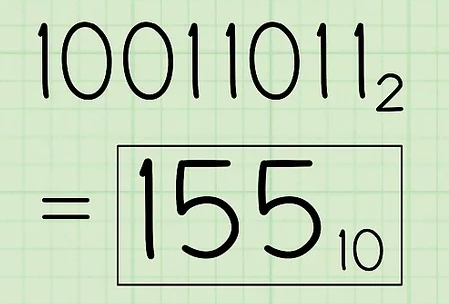 Переводим числа между двоичной и десятичной системами «на лету», объяснение «на пальцах»Вступление: А что-же тянуть. Все что будет дальше, пойдет на тему подсчета в двоичной системе на пальцах. Кто еще не знает, постараюсь объяснить, что это, как и зачем это осваивать. Начну, пожалуй, с преимуществ: 1. Удобно переводить любое число с десятичной в двоичную системы и наоборот, не используя калькулятор. 2. Развивается моторика пальцев. 3. Развивается визуальное восприятие двоичных чисел. Минусы: 1. Немного тренировки. 2. Нельзя в публичных местах показывать числа 26,27,352,378 и 891. Суть: Многим, наверняка, приходилось переводить между системами. И я думаю многие запомнили, что: 2-10 3-11 4-100 5-101 и т.д. Логично, что исходя из того что каждая разрядность имеет два состояния, мы можем изобразить это дело на пальцах. Поставьте перед собой руку (ладонью к себе), согните большой палец. Вот и есть единица. Разогните большой и согните указательный, вот и два. Тоесть разогнутый палец — это 0, а согнутый — 1. Так как начальные нули отбросились, мы имеем отсчет от «самой левой» единицы. Названия пальцев — те которые загнуты: средний, большой — 101 — 5 безымянный, средний -1100 — 12 мизинец, средний — 10100 — 20 Чтобы загибать мизинец, понадобиться некоторая практика. Но суть в другом. Представим разрядность каждого пальца руки, как 2^n (на фото)  То есть,  Теперь, представим, что нам нужно перевести число 25 в двоичную. Загибаем Мизинец — 16, Безымянный — 8 и большой — 1. т.к. 16+8+1=25.  Если не поняли, то вот еще пример, число 14, думаем: Мизинец — это много, средний нормально, но можно взять больше, поэтому — загибаем безымянный, это 8. Запомнили, далее средний — +4, єто уже 12 и указательный — +2, итог 14.  Так же поступаем с двоичными. Вот например видим где-то: 1011101. Представляем это на руках с разрядностями (уже две руки).  64+16+8+4+1=93 Имеем: 1011101(2) = 93(10) Заключение: таким образом мы можем использовать данный метод от 0 до 1023, используя пальцы и обладая элементарной арифметикой. Но при добавлении, хотя бы, одного разряда, можно будет считать до 2047, и далее до 4095, 8191 и т.д. А это могут быть руки, ноги, веки, либо что-то еще что может иметь два состояния 1 и 0. |
