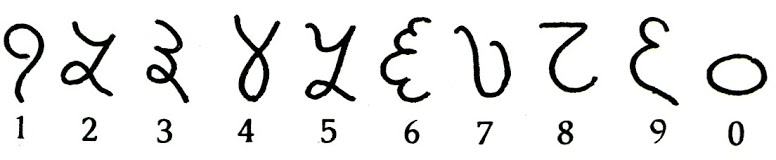|
|
Как появились цифры и числа
Можно ли представить мир без чисел?
Люди так часто пользуются числами и счетом, что трудно даже представить себе, что они существовали не всегда, а были изобретены человеком.
КАК ПОЯВИЛИСЬ ЦИФРЫ И ЧИСЛА.
1. Арифметика каменного века.
Сначала люди научились узнавать число предметов или животных, делая особые зарубки на счетных палочках, вести счет.
Мысль о счете пришла людям в голову раньше, чем появились цифры. Люди могли сообщить друг другу, что в одном стаде животных больше чем в другом, а вот, сколько именно – сосчитать не умели.
Древние люди не умели считать. Да и считать им было нечего, потому что предметов, которыми они пользовались – орудий труда, - было совсем немного: один топор, одно копье… Постепенно количество вещей увеличивалось, обмен ими все усложнялся и возникла потребность в счете.
Несколько десятков лет назад ученые-археологи обнаружили стойбище древних людей. В нем они нашли волчью кость, на которой 30 тысяч лет тому назад какой-то древний охотник нанес 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам. Узор на кости состоял из 11 групп, по 5 зарубок в каждой. При этом первые 5 групп он отделил от остальных длинной чертой. Позднее в Сибири и других были найдены сделанные в ту далекую эпоху каменного века (каменные орудия) и украшения, на которых тоже были черточки и точки, сгруппированные по 3, по 5 или по 7. Много тысячелетий прошло с того времени. Но и сейчас швейцарские крестьяне, отправляя молоко на сыроварни, отмечают число фляг такими же зарубками. До сих пор в русском языке сохранилось слово «бирка». Теперь так называют дощечку с номером или надписью, которую привязывают к кулям с товаром, ящикам и тюкам и т.д. А еще двести –триста лет назад это слово означало совсем иное. Так называли куски дерева, на которых зарубками отмечали сумму долга и подати. Бирку с зарубками раскладывали пополам, после чего одна половинка оставалась у должника, а другая у сборщика податей. При счёте
половинки складывали вместе, и это позволяло определить сумму долга или подати без спора и сложных вычислениях.
2. Числа начинают получать имена.
Они могли представить себе такие числа как один, два, три. Все другие числа они означали понятием «Много». Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.
Ещё недавно существовали племена, в языке которых были названия только двух чисел: «один» и «два». Туземцы островов, расположенных в Торресовом проливе, знали два числа: «урапун» - один, «окоза» - два и умели считать до шести. Островитяне считали так: «окоза-урапун» - три, «окоза-окоза» - четыре, «окоза-окоза-урапун» - пять, «окоза-окоза-окоза» - шесть. О числах, начиная с 7, туземцы говорили «много», «множество». Наши предки, наверняка, тоже начинали с этого. В старинных пословицах и поговорках как, например, «Семеро одного не ждут», «Семь бед – один ответ», «У семи нянек дитя без глазу», «Один с сошкой, семеро с ложкой» 7 тоже означало «много».
В древние времена, когда человек хотел показать, сколькими животными он владел, он клал в большой мешок столько камешков, сколько у него было животных. Чем больше животных, тем больше камешков. Отсюда и произошло слово «калькулятор», «калькулюс» по латински означает «камень».
Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги. Поэтому, если в те времена кто-то хвалился, что у него «две руки и одна нога кур», это означало, что у него пятнадцать кур, а если это называлось «весь человек», то есть две руки и две ноги.
Перуанские инки вели счет животных и урожая, завязывая узелки на ремешках или шнурках разной длины и цвета (Рис. 1). Эти узелки назывались кипу. У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают 4 узелочка шнурочке! Поэтому того, кто завязывал узелки, называли вспоминателем.

рис.1
Первыми придумали запись чисел древние шумеры. Они пользовались всего двумя цифрами. Вертикальная чёрточка обозначала одну единицу, а угол из двух лежачих чёрточек – десять. Эти чёрточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали. Вот так выглядели эти дощечки (Рис. 2).
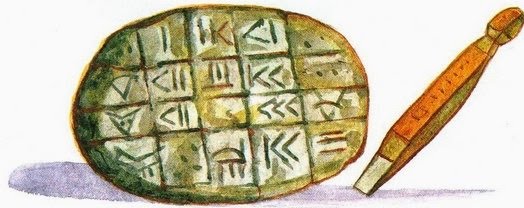
рис.2
После счета по зарубкам люди изобрели особые символы, названные цифрами. Они стали применяться для обозначения различных количеств каких-либо предметов. Разные цивилизации создавали свои собственные цифры.
Так, например, в древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки (иероглифы) для записи чисел 1, 10, 100, 1000, …: (Рис. 3).
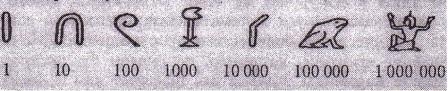
рис.3
Для того чтобы изобразить, например, целое число 23145, достаточно записать в ряд два иероглифа, изображающие десять тысяч, затем три иероглифа для тысячи, один – для ста, четыре – для десяти и пять иероглифов для единицы: (Рис.4).

рис.4
Этого одного примера достаточно, чтобы научиться записывать числа так, как их изображали древние египтяне. Это система очень проста и примитивна.
Похожим образом обозначали числа на острове Крит, расположенном в Средиземном море. В критской письменности единицы обозначались вертикальной чёрточкой |, десятки – горизонтальной - , сотни – кружком ◦, тысячи – знаком ¤.
Народы (вавилоняне, ассирийцы, шумеры), жившие в Междуречье Тигра и Евфрата в период от II тысячелетия до н.э. до начала нашей эры, сначала обозначали числа с помощью кругов и полукругов различной величины, но затем стали использовать только два клинописных знака – прямой клин q(1) и лежащий клин t (10). Эти народы использовали шестидесятеричную систему счисления, например число 23 изображали так: t t qqq Число 60 снова обозначалось знаком q, например число 92 записывали так: qtttqq
В начале нашей эры индейцы племени майя, которые жили на полуострове Юкатан в Центральной Америке, пользовались другой системой счисления – двадцатеричной. Они обозначали 1 точкой, а 5 – горизонтальной чертой, например, запись ‗‗‗‗‗‗означала 14. системе счисления майя был и знак для нуля. По своей форме он напоминал полузакрытый глаз.
В Древней Греции сначала числа 5, 10, 100, 1000, 10000 обозначали буквами Г, Н, Х, М, а число 1 – черточкой /. Из этих знаков составляли обозначения r r r Г (35) и т.д. Позднее числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000, 20000 стали обозначать буквами греческого алфавита, к которому пришлось добавить еще три устаревшие буквы. Чтобы отличить цифры от букв, над буквами ставили черточку.
Древние индийцы изобрели для каждой цифры свой знак. Вот как они выглядели (Рис.5)
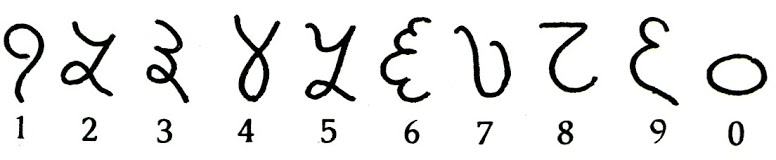
рис.5
Однако Индия была оторвана от других стран, - на пути лежали тысячи километров расстояния и высокие горы. Арабы были первыми «чужими», которые заимствовали цифры у индийцев и привезли их в Европу. Чуть позже арабы упростили эти значки, они стали выглядеть вот так (Рис.6)
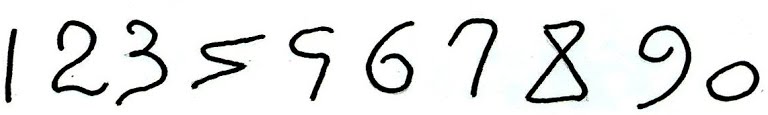
рис.6
Они похожи на многие наши цифры. Слово «цифра» тоже досталось нам от арабов по наследству. Арабы нуль, или «пусто», называли «сифра». С тех пор и появилось слово «цифра». Правда, сейчас цифрами называются все десять значков для записи чисел, которыми мы пользуемся: 0, 1, 2,3,4,5,6,7,8,9.

Постепенное превращение первоначальных цифр в наши современные цифры.
3. Римские цифры.
Из всех странных нумераций римская является единственной, сохранившейся до сих пор и довольно широко применяемой. Римские цифры употребляются и сейчас для обозначения столетий, нумерации глав в книгах и др.
Для записи чисел в римской нумерации надо запомнить изображение семи чисел .
I V X L C D M
1 5 10 50 100 500 1000
С их помощью можно записать любое число не больше 4000. Некоторые числа записываются при помощи повторения римских цифр:
III = 3 · 1 = 3, XX = 2 · 10 = 20.
Кроме того, используется принцип сложения и вычитания. Если меньшая по значению буква стоит после большей, то их значения складывают:
VI = 5 + 1 = 6, MC = 1000 + 100 = 1100
Если меньшая цифра стоит перед большей, то из большего вычитают меньшее:
IV = 5 – 1 = 4, СМ = 1000 – 100 = 900.
Задание. Какие числа обозначают запись: ХХХVI, СХLV ?
(ХХХVI = 3 · 10 + (5 + 1) = 36,
CXLV = 100 + (50 – 10) + 5 = 145.)
4.Цифры русского народа.
Наши предки пользовались алфавитной нумерацией, то есть числа изображались буквами, над которыми ставился значок , называемый «титло». Чтобы отделить такие буквы – числа от текста, спереди и сзади ставились точки.
Этот способ обозначения цифр называется цифирью. Он был заимствован славянами от средневековых греков – византийцев. Поэтому цифры обозначались только теми буквами, для которых есть соответствия в греческом алфавите (Рис. 7).

Для обозначения больших чисел славяне придумали свой оригинальный способ:
Десять тысяч – тьма,
десять тем – легион,
десять легионов – леорд,
десять леордов – ворон,
десять воронов – колода.

Такой способ обозначения чисел по сравнению с принятой в Европе десятичной системой был очень неудобен. Поэтому Пётр I ввёл в России привычные для нас десять цифр, отменив буквенную цифирь.
5. САМЫЕ НАТУРАЛЬНЫЕ ЧИСЛА.
Ряд чисел 1,2,3,4,5,6,7,8,9… называется натуральным. А сами эти числа натуральными. Возник этот ряд в глубокой древности, когда у людей возникла потребность в счете предметов. С появлением натурального ряда был сделан первый шаг к созданию математики. Сейчас все понимают, что натуральный ряд чисел бесконечен. В древности люди этого не знали. Сначала они умели считать до трех, потом до десяти, до сорока, до ста, а дальше была «тьма». Натуральный ряд был очень коротким. Расширить его удалось великому механику и математику древности Архимеду. Архимед написал знаменитый труд Псаммит, или Исчисление песчинок». В нем он подсчитал число песчинок, которые могли бы заполнить шар радиусом 15.000.000.000.000 километров. До Архимеда в Древней Греции самым большим числом считалось 10.000.000 мириад. Мириадой называлось число 10000, от греческого слова «мирос» - «неисчислимо большое». Архимед начал считать мириадами мириад и в результате вывел свою систему счисления. Наибольшее число его системы содержит 80.000.000.000.000.000 нулей. Это число так велико, что если напечатать его обыкновенным шрифтом на машинке, то этой лентой можно опоясать Земной шар по экватору более 2 миллионов раз. Даже ракете с первой космической скоростью (8км/с) пришлось бы лететь вдоль этой ленты более 300 лет.
Вот до какого огромного числа простирается натуральный ряд. Но и это число не последнее. За ним еще числа, числа, числа, числа… до бесконечности. Если натуральный ряд чисел кажется вам скучным и однообразным, всмотритесь в него повнимательнее, и вы найдете много удивительного и неожиданного.
Например, обыкновенное число 37. А теперь умножьте его на три, потом на шесть и так далее… На этом чудеса числа 37 не кончаются. Возьмем любое трехзначное число, которое делится на 37. Пусть это будет 185. И сделаем в нем круговую перестановку – последнюю цифру поставим на первое место, не изменив порядка остальных. Получим 518. Сделаем еще одну перестановку. Получим 851. Оба эти числа также делятся на 37. Вот вам и диковинка!
|
|
|
 Скачать 263.7 Kb.
Скачать 263.7 Kb.