кАРТОЧКИ ПО МАТЕМАТИКЕ. Карточки по математике; Подготовка к ЕГЭ профильный уровень. Карточки для подготовки к егэ по математике (профильный уровень)
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
Карточки для подготовки к ЕГЭ по математике (профильный уровень) Карточка № 1. Найдите объём многогранника, вершинами которого являются вершины А, В, С, D, В1 прямоугольного параллелепипеда АВСDА1В1С1D1, у которого АВ =9, ВС =3, ВВ1 =8.  Имеются два сосуда. Первый содержит 55кг, а второй -20кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если смешать равные массы этих растворов, то получится раствор, содержащий 75% кислоты. Сколько процентов кислоты содержится в первом сосуду? Велосипедист совершает n оборотов педалей велосипеда, а велосипедист при этом проходит путь, который можно найти по формуле S = 2 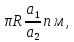 где R – радиус колеса в метрах, а1 и а2 - количество зубцов на большой и малой звездочках велосипеда соответственно. Какой путь пройдет велосипедист при 13 оборотах педалей, если на большой - звездочке 40 зубьев, на малой – 15, а диаметр колеса 57см. Считайте, что где R – радиус колеса в метрах, а1 и а2 - количество зубцов на большой и малой звездочках велосипеда соответственно. Какой путь пройдет велосипедист при 13 оборотах педалей, если на большой - звездочке 40 зубьев, на малой – 15, а диаметр колеса 57см. Считайте, что 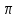 = 3,14. Результат округлите до целого числа метров. = 3,14. Результат округлите до целого числа метров.Найдите корень уравнения 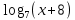 = 1 + = 1 + 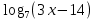 . .
Найдите sin 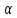 , если соs , если соs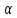 = = 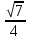 и и 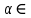 ( ( 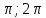 ). ).В какой точке функция у = 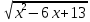 принимает наименьшее значение. принимает наименьшее значение.Боковые стороны трапеции, описанной около окружности, равны 25 и 3. Найдите среднюю линию трапеции. 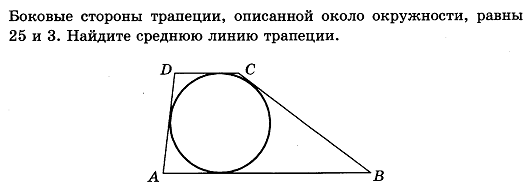 Карточка № 2. Объём параллелепипеда АВСDА1В1С1D1 равен 6. Найдите объём треугольной пирамиды АD1СВ1. 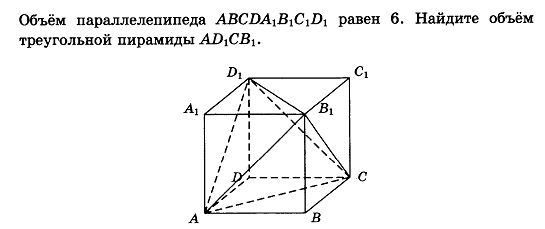 На клетчатой бумаге с размером клетки 1 х 1 изображен четырёхугольник. Найдите его площадь.  Найдите значения выражения 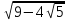 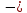 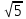 Найдите точку максимум функции у = (х +7)2 е-1- х Высота деревянного стеллажа для книг равна h = (а + b) n +a (в миллиметрах), где a – толщина одной доски (в мм), b – высота одной полки (в мм), n - число таких полок. Найдите высоту книжного стеллажа из 8 полок, если a= 18мм, b = 310мм. Ответ дайте в миллиметрах. В цилиндрическом сосуде уровень жидкости достигает 45см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 1,5 раза больше диаметра первого?  Гигрометр измеряет влажность в помещении картинной галереи. Вероятность того, что влажность окажется выше 40%, равна 0,82. Вероятность того, что влажность находится в пределах ниже 56%, равна 0,74. Найдите вероятность того, что влажность находится в пределах от 40% до 56%. Угол АВС равен 54о. Градусная мера дуги АВ окружности, не содержащей точек D и С, равна 138о. Найдите угол ВАС. Ответ дайте в градусах. Карточка № 3. На автомобильной шине с помощью специальной маркировки указаны её размеры. Например, 265/60R18. Первое число означает ширину шины В (в мм). Второе число означает отношение высоты профиля шины Н к ширине шины в процентах. Буква означает конструкцию шины (R – радиальный тип), а последнее колеса число означает диаметр обода колеса d в дюймах. На автомобиле «Лада – Калина» завод устанавливает шины с маркировкой 185/60R14. Найдите диаметр колеса D этого автомобиля. В одном дюйме 25,4мм. Ответ дайте в сантиметрах с округлением до целого.  Через среднюю линию основания треугольной призмы проведена плоскость, параллельна боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 36. Найдите площадь боковой поверхности исходной призмы.  Найдите значение выражения 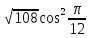 – – 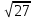 . .Найдите наименьшее значение функции у = (х – 10)2 (х + 1) + 3 на отрезке 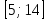 . .Артём гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что таким образом он выйдет к пруду или фонтану. 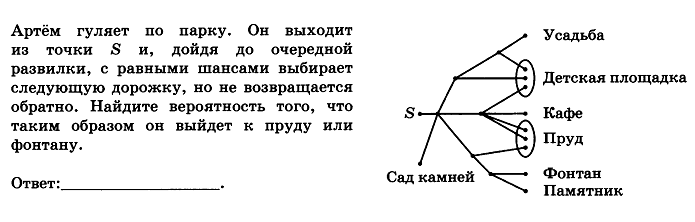 Найдите наибольший отрицательный корень уравнения sin 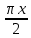 = = 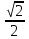 . .Найдите корень уравнения 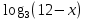 = 3 = 3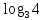 . .Карточка № 4. 1. На фабрике керамической посуды 30% произведенных тарелок имеют дефект. При контроле качества продукции выявлено 58% дефектных тарелок. Остальные тарелки поступили в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефекта. Ответ округлите до сотых. 2. Водолазный колокол, содержащий v =3 моля воздуха при давлении р1 = 1,8 атмосферы, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха до конечного давления р2. Работа, совершаемая водой при сжатии воздуха, определяется выражением A = 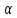 vlog2 vlog2 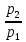 , , где , , где 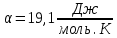 — постоянная, — постоянная, 3. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 3 рабочих, а во второй -9 рабочих. Через 4 часа после начала работы в первую бригаду перешли 7 рабочих из второй бригады. в итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов. 4. На рисунке изображен график функции у = f(х) и на оси абсцисс отмечены точки: -7; -3; 1; 7. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку. 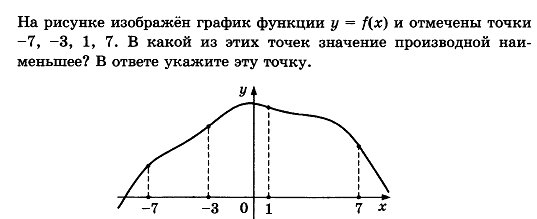 5. В сосуде, имеющем форму конуса, уровень жидкости достигает 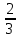 высоты. Объём жидкости равен 152мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? высоты. Объём жидкости равен 152мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд? 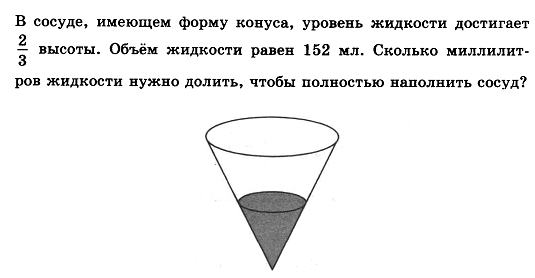 6. Основания равнобедренной трапеции равны 48 и 20. Центр окружности, описанной около трапеции лежит, внутри трапеции, а радиус окружности равен 26. Найдите высоту трапеции. 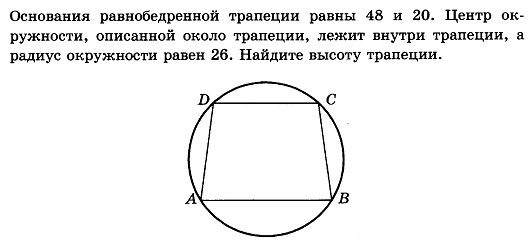 7. Найдите наибольшее значение функции у = 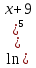 на отрезке на отрезке 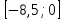 . .Карточка № 5. В июле на рынке голландские помидоры стоили на 25% дешевле краснодарских; в августе они подорожали на 10%, а краснодарские помидоры подешевели на 40% за счёт сезонного падения цен. На сколько процентов голландские помидоры дороже краснодарских в августе. Найдите значение выражения 3 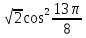 - 3 - 3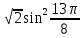 . .В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые ребра призмы равны 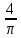 . Найдите объём цилиндра, описанного около этой призмы. . Найдите объём цилиндра, описанного около этой призмы. Объём правильной четырехугольной пирамиды SАВС D равен 52. Точка Е – середина ребра SВ. Найдите объём треугольной пирамиды ЕАВС.  м/с2 м/с2Небольшой мячик бросают под острым углом 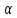 к плоской горизонтали поверхности земли. Максимальная высота полёта мячика, выражается в метрах, определяется формулой к плоской горизонтали поверхности земли. Максимальная высота полёта мячика, выражается в метрах, определяется формулой Н = 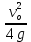 (1 – соs 2 (1 – соs 2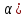 , где , где 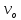 = 26 м/cначальная скорость мячика, а g – ускорение свободного падения ( считайте g = 10 м/с2). При каком наименьшем значении угла = 26 м/cначальная скорость мячика, а g – ускорение свободного падения ( считайте g = 10 м/с2). При каком наименьшем значении угла 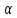 (в градусах) мячик пролетит над стеной высотой 7,45 м на расстоянии 1м? (в градусах) мячик пролетит над стеной высотой 7,45 м на расстоянии 1м?Клиент получает в банке кредитную карту. Четыре последние цифры номера карты случайные. Какова вероятность того, что эти последние четыре цифры идут подряд в порядке убывания, например, 3210 или 6543. Найдите наименьшее значение функции у = е2х – 4ех +7 на отрезке 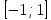 . .Чайные клиперы – самые быстрые парусные корабли. Некоторые из них могли развивать скорость до 20 узлов. Переведите в километры в час скорость клипера, который делает 15 узлов. 1 узел равняется 1 морской миле в час. 1 морская миля равняется 1852 метрам. Результат округлите до целого числа километров в час. Карточка № 6. Найдите угол АСО, если его сторона СА касается окружности с центром О, отрезок СО пересекает окружность в точке В, а дуга АВ окружности заключённая внутри этого угла равна 17о. Ответ дайте в градусах.  Найдите наибольшее значение функции у = 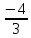 х х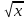 + 6х +13. + 6х +13.В треугольнике АВС угол С равен 90о, АВ = 9, tqА = 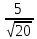 . Найдите АС. . Найдите АС.Шар вписан в цилиндр. Площадь поверхности шара равна 26. Найдите площадь полной поверхности цилиндра.  На рисунке изображен график функции у = f(х) На оси абсцисс и отмечены точки: -2; -1; 2; 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку. 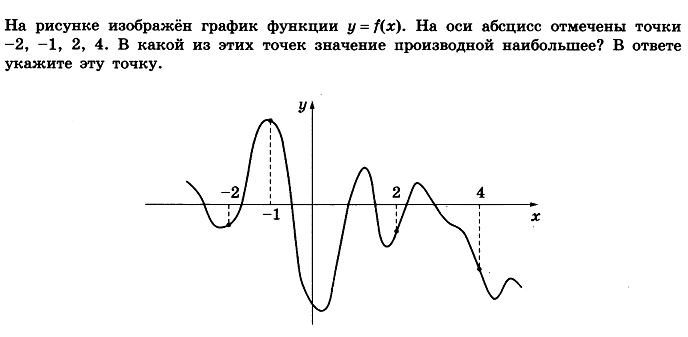 Какова вероятность того, что последние цифры телефонного номера случайного абонента в сумме дают 10? На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 5. найдите площадь заштрихованной фигуры. 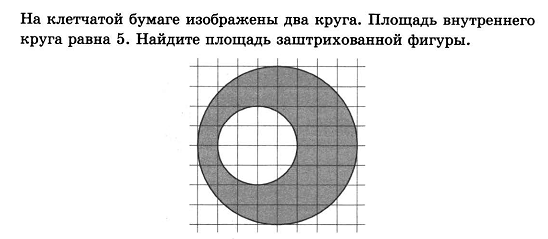 При адиабатическом процессе для идеального газа выполняется закон 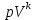 =3,2 =3,2 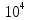 Па Па 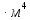 где р – давление в газе в паскалях, V- объём газа в кубических метрах, k = 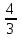 . . Найдите, Найдите, какой объём V(в куб.) будет занимать газ при давлении р, равном 2 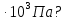 Ответы:
|
