РГР Нарипов. Казахский агротехнический университет им с. Сейфуллина
 Скачать 86.48 Kb. Скачать 86.48 Kb.
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РЕСПУБЛИКИ КАЗАХСТАН КАЗАХСКИЙ АГРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ С.СЕЙФУЛЛИНА Расчетно-графическая работа] Выполнил: Нарипов Адильбек Батырулы  Проверил: Альпеисов Есенбай Ашималиевич Проверил: Альпеисов Есенбай АшималиевичНур-Султан 2022 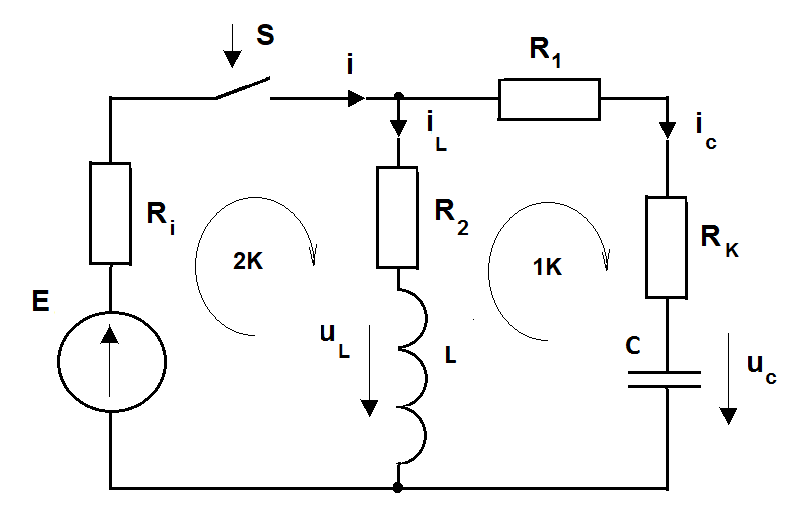 Дано: E = 8 B L = 9 мГн C = 20 мкФ 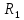 = 45 Ом = 45 Ом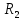 = 16 Ом = 16 Ом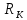 = 15 Ом = 15 Ом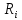 = 5 Ом = 5 ОмНайти: 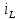 (t) (t)Решение: 1)Составим систему дифференциальных и алгебраических уравнений по первому и второму законам Кирхгофа для заданной электрической схемы после коммутации (замыкания ключа S). Схема состоит из трех ветвей и двух узлов. 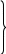 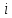 - - 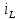 - - 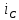 = 0 = 0- 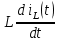 - -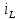 * *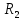 + + 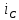 *( *(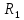 + +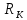 ) + ) + 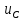 = 0 = 0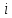 * *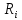 + + 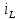 * *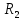 + + 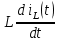 =E =E2) Независимые начальные условия состоят из напряжения на емкости и тока через индуктивности в момент коммутации, т.е. 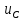 ( (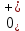 ) и ) и 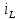 ( (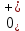 ) )Для получения этих значений воспользуемся первым и вторым законами коммутации: 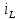 ( (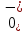 ) = ) = 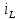 ( (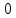 ) = ) = 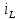 ( (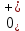 ) и ) и 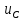 ( (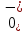 ) = ) = 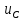 ( (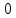 ) = ) = 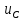 ( (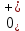 ) )Изобразим схему цепи до коммутации: 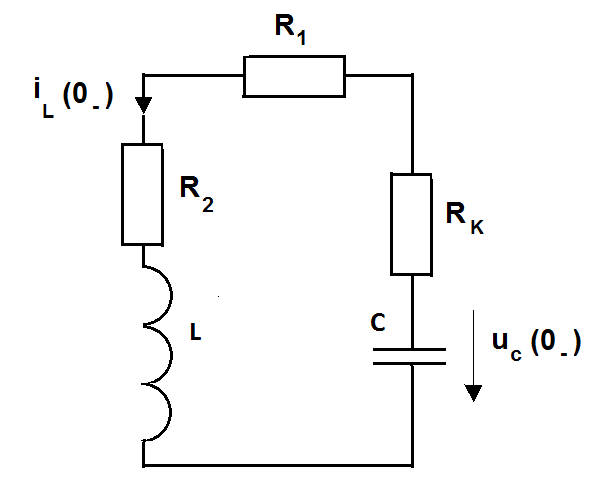 В этой цепи отсутствуют источники энергии, конденсатор до коммутации не был заряжен, следовательно: 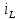 ( (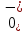 ) =0 ) =0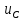 ( (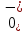 ) =0 ) =0Тогда согласно законам коммутации напряжение на емкости и ток через индуктивности в момент коммутации 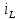 ( ( ) =0 ) =0 ( ( ) =0 ) =03)Расчет принужденного режима. Принужденный (установившийся) режим при постоянном источнике ЭДС установится после коммутации через относительно длительное время, когда по ветвям заданной цепи будут протекать установившиеся, постоянные токи. В установившемся режиме заданная схема приобретает следующий вид:  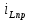 = = 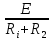 = = 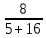 = 0,381 A = 0,381 A4)Определение корней характеристического уравнения. Для определения корней характеристического уравнения изобразим схему так, как показано ниже. При этом индуктивное сопротивление изобразим в виде pL, а емкостное сопротивление в виде 1/pC, исходя из того, что jω заменяем на р, т.е. jω = р. Входное сопротивление в схеме определяется относительно источника ЭДС, для этого в качестве точки разрыва выбираются вход и выход ЭДС в схеме. Таким образом исходная схема представляется в виде: 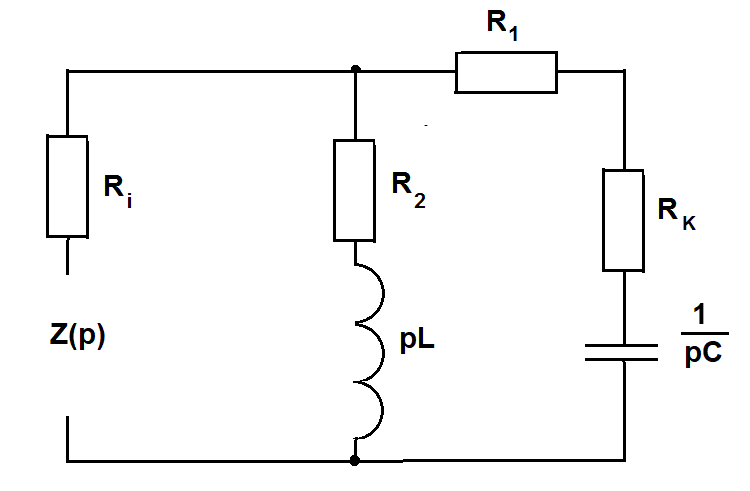 Рассчитаем входное сопротивление (эквивалентное сопротивление) относительно точек разрыва: Z(p) = 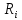 + + 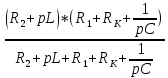 Для определения характеристического уравнения цепи приравняем к нулю это сопротивление и преобразуем его 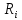 + + 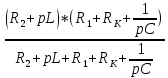 = 0 = 0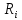 *( *(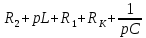 )+ )+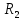 *( *(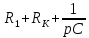 )+pL*( )+pL*(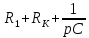 )= 0 )= 0C*L*( 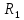 + + 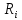 + +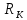 )* )*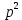 +[L+C*( +[L+C*(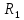 * *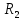 + +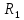 * *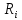 + +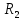 * *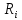 + +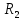 * *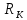 + +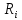 * *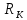 )]*p + )]*p +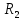 + +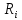 =0 =0Подставляем в полученное уравнение все заданные числовые значения: 20* 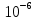 *9* *9*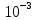 *( *(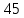 + + 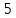 + +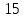 )* )*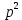 + ++ [9* 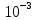 +20* +20*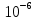 *( *(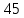 * *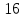 + +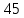 * *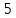 + +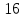 * *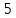 + +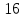 * *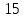 + +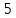 * *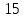 p + p +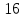 + +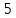 =0 =0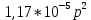 +0,036 +0,036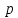 +21 = 0 +21 = 0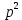 +3,06* +3,06*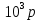 +1,8* +1,8*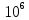 = 0 = 0В результате получили алгебраическое уравнение второго порядка (квадратное уравнение). Находим корни полученного уравнения: 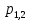 = - 1,53* = - 1,53*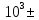 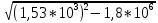 = - 1,53* = - 1,53*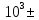 739 c-1 739 c-1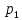 = = 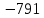 c-1 c-1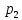 = = 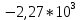 c-1 c-1Корни вещественные и различные, следовательно, переходной процесс будет апериодическим. В данном случае свободные составляющие имеют вид: 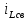 = = 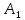 * *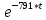 + + 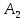 * *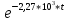 Полный ток в индуктивности будет равен: 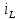 = 0,381 + = 0,381 + 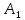 * *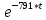 + + 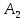 * *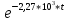 5) В этом уравнении неизвестными являются постоянные интегрирования  и и  . Для этих двух неизвестных необходимо составить два уравнения. . Для этих двух неизвестных необходимо составить два уравнения. Первое уравнение для определения  и и  получим, используя значения п.2, т.е. значение тока через индуктивность в момент коммутации (t = 0): получим, используя значения п.2, т.е. значение тока через индуктивность в момент коммутации (t = 0):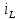 ( (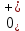 ) = ) = 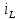 ( (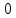 ) = 0,381 + ) = 0,381 + 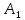 + + 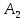 Учтем независимые начальные условия 0,381 + 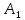 + + 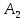 = 0 = 0Для получения второго уравнения необходимо определить зависимые начальные условия из системы уравнений п.1 для момента времени t(0+) (момент коммутации): 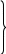 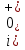 - - 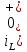 - - 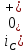 = 0 = 0- 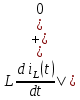 - -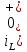 * *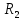 + + 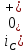 *( *(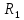 + +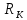 ) + ) + 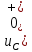 = 0 = 0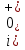 * *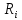 + + 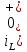 * *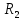 + + 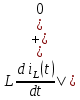 =E =EПодставим в нее независимые начальные условия Решение системы: 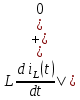 = 7,39 B = 7,39 B т.е. 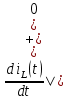 = = 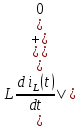 = = 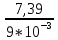 = 821 A/c (*) = 821 A/c (*)Продифференцируем выражение тока 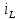 , полученное в п.4: , полученное в п.4: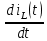 = = 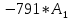 * *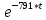 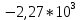 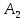 * *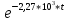 В момент времени t=0+ (в момент коммутации) : 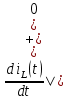 = = 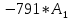 - - 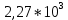 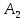 Учтем полученное выше равенство (*) и получим второе уравнение: 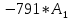 - - 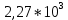 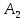 = 821 = 821Решаем систему, состоящую из двух уравнений: 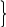 0,381 + 0,381 + 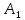 + + 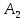 = 0 = 0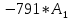 - - 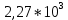 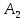 = 821 = 821 Решение системы 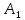 = -0,03 A = -0,03 A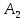 = -0,351 A = -0,351 Aокончательное выражение тока iL(t): 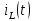 = 0,381 - 0,03* = 0,381 - 0,03*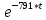 - 0,351* - 0,351*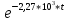 A AСтроим график 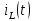 в интервале 0 в интервале 0 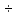 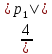 = 0 = 0  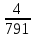  0 0  0,005 c 0,005 c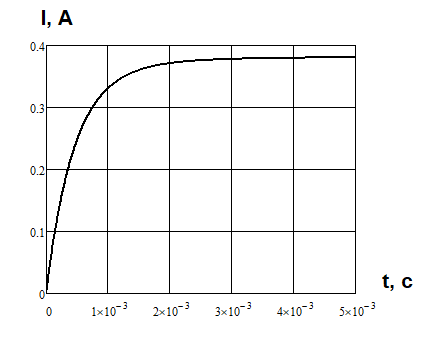 |
