Курс работа пример. Кинематический анализ механизма
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
Пример Произвести кинематический и силовой анализы кривошипно-шатунного механизма, показанного на рисунке 1. Ведущим звеном является кривошип 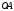 , частота вращения которого постоянна и равна , частота вращения которого постоянна и равна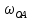 =75,36 =75,36 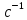 , угловое ускорение , угловое ускорение 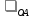 =0, длина кривошипа =0, длина кривошипа 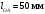 , длина шатуна , длина шатуна 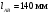 , угол , угол  между горизонталью и положением кривошипа составляет между горизонталью и положением кривошипа составляет 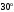 . Точка . Точка 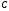 лежит посередине шатуна лежит посередине шатуна 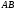 . Направление угловой скорости ведущего звена . Направление угловой скорости ведущего звена 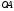 указано на рисунке. В задании нужно построить планы скоростей и ускорений механизма, определить скорости и ускорения точек указано на рисунке. В задании нужно построить планы скоростей и ускорений механизма, определить скорости и ускорения точек  , ,  и и 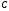 . Определить опорные реакции и реакции в шарнире . Определить опорные реакции и реакции в шарнире  , масса кривошипа , масса кривошипа 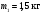 и сосредоточена она в т. О, масса шатуна и сосредоточена она в т. О, масса шатуна 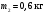 , масса ползуна , масса ползуна 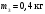 . Кривошип ОА и шатун . Кривошип ОА и шатун 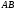 считать однородными тонкими стержнями с постоянным поперечным сечением. Масса кривошипа сосредоточена в т. О, масса шатуна сосредоточена в точке С, размеры ползуна В не учитываются, а его масса считается сосредоточенной в точке В. Сила полезного сопротивления F, действующая на ползун В, является постоянной по величине и равна считать однородными тонкими стержнями с постоянным поперечным сечением. Масса кривошипа сосредоточена в т. О, масса шатуна сосредоточена в точке С, размеры ползуна В не учитываются, а его масса считается сосредоточенной в точке В. Сила полезного сопротивления F, действующая на ползун В, является постоянной по величине и равна  . .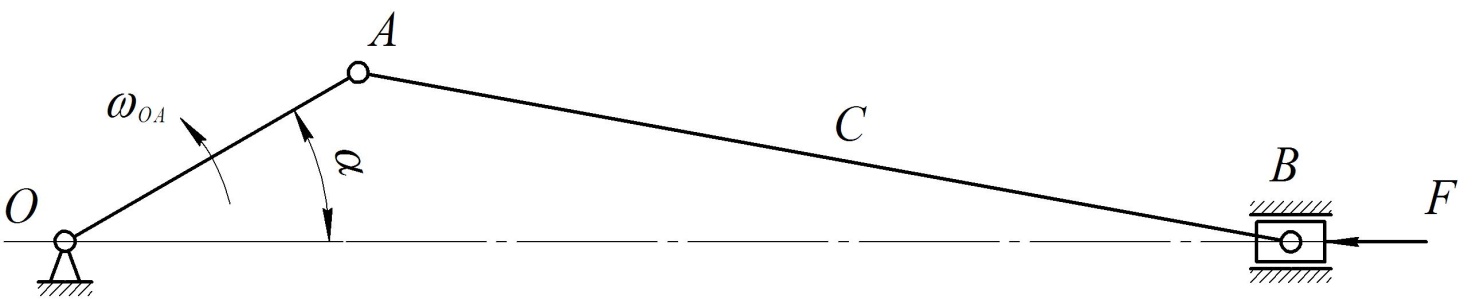 Рисунок 1. Схема кривошипно-шатунного механизма ) Кинематический анализ механизма Кинематический анализ механизма состоит в определении движения звеньев механизма по заданному движению ведущих звеньев. Кинематический анализ, осуществляемый при помощи графических методов, начинается с построения плана механизма, то есть с графического изображения взаимного расположения звеньев механизма, соответствующего заданному положению его ведущего звена. План механизма должен быть построен в определенном чертежном масштабе, например 1:2, 1:1, 2:1 и т.д. В нашем случае для размещения плана механизма на листе формата А2, вполне подходит чертежный масштаб 1:1. Построив план механизма, указываем на нем направления угловой скорости и углового ускорения ведущего звена 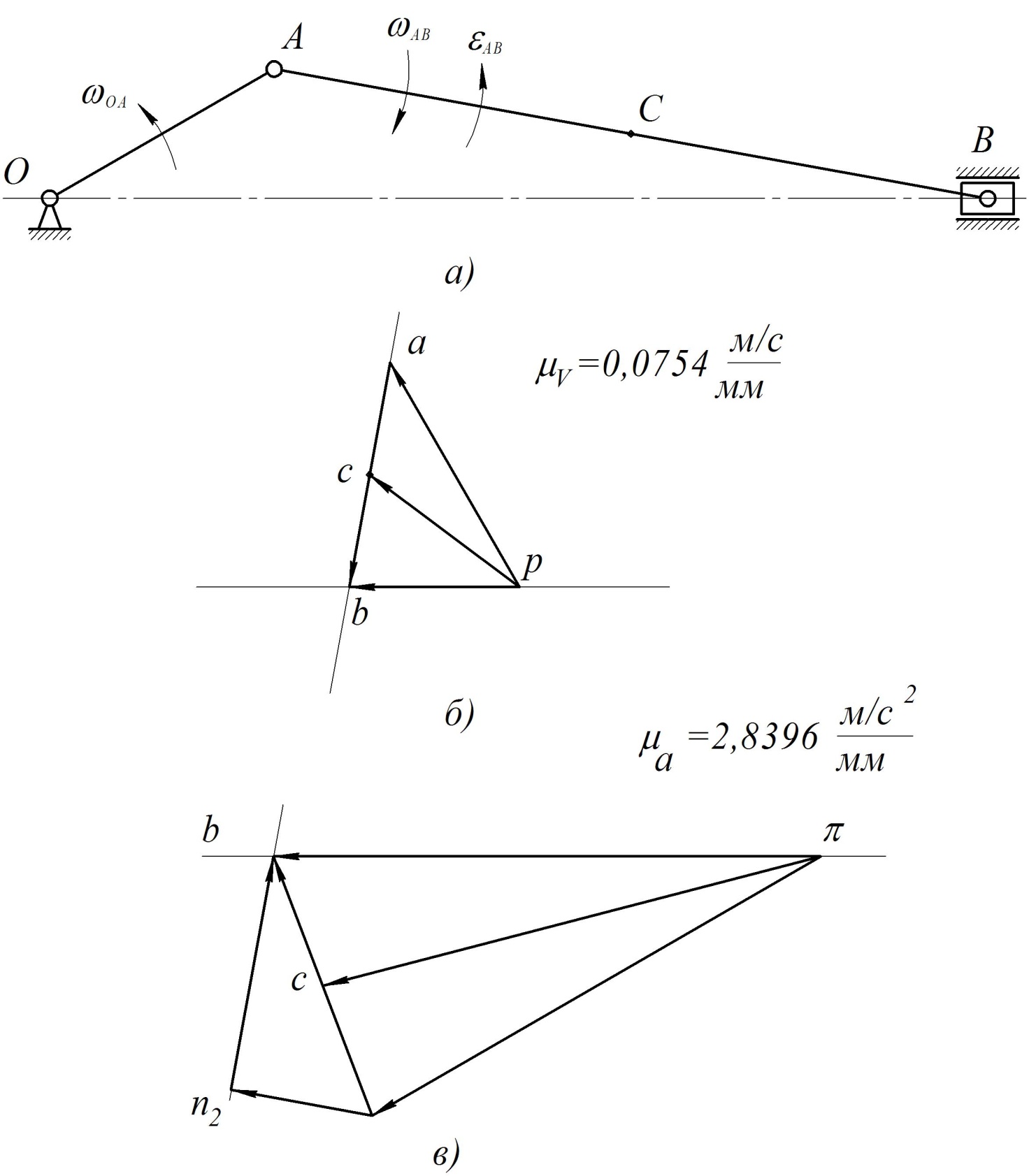 Рисунок 2. Планы механизма, скоростей и ускорений Далее строятся планы скоростей и ускорений механизма, находящегося в том положении, в котором он построен на плане механизма. Дадим определение этих понятий. Планом скоростей называют чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек механизма в данном положении. Планом ускорений называется чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению ускорениям различных точек механизма в данном положении. В качестве масштаба построения планов скоростей и ускорений обычно выбирается масштабный коэффициент. Поясним различия между масштабом и масштабным коэффициентом. Масштабом физической величины называют длину отрезка в миллиметрах, изображающую единицу измерения этой величины. Масштабным коэффициентом физической величины называют отношение численного значения физической величины в свойственных ей единицах к длине отрезка в миллиметрах, изображающего эту величину. Задача об определении скоростей, которую будем решать путем построения плана скоростей, формулируется следующим образом. Дан план механизма с указанием всех размеров, его определяющих, задана начальная угловая скорость и угловое ускорение ведущего звена Кривошип 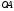 является ведущим звеном, который совершает равномерное вращательное движение вокруг точки является ведущим звеном, который совершает равномерное вращательное движение вокруг точки 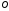 . Шатун . Шатун 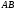 совершает плоскопараллельное движение. Ползун совершает плоскопараллельное движение. Ползун  движется по горизонтальной направляющей и совершает поступательное движение. движется по горизонтальной направляющей и совершает поступательное движение.Построение планов скоростей и ускорений механизма начинается с ведущего звена. Поэтому сначала найдем величину скорости точки  ведущего звена ведущего звена 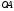 : :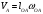 . .Найдем угловую скорость 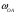 звена звена 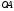 исходя из известной частоты вращения этого звена: исходя из известной частоты вращения этого звена: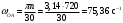 Тогда скорость точки  : :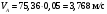 . .Изобразим скорость 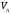 вектором, отложенным от некоторой точки вектором, отложенным от некоторой точки 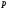 , называемой полюсом плана скоростей (рис. 2б). Положение точки , называемой полюсом плана скоростей (рис. 2б). Положение точки 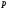 на чертеже определяется произвольно, в том месте, где это будет удобно для дальнейшего построения плана скоростей. Вектор скорости точки на чертеже определяется произвольно, в том месте, где это будет удобно для дальнейшего построения плана скоростей. Вектор скорости точки  направлен перпендикулярно ведущему звену направлен перпендикулярно ведущему звену 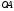 в сторону угловой скорости в сторону угловой скорости 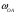 : :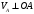 . .В конце вектора, обозначающего скорость точки  , поставим точку , поставим точку  . Длина отрезка . Длина отрезка 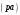 принимается произвольно. Мы зададим длину принимается произвольно. Мы зададим длину 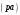 равной длине ведущего звена равной длине ведущего звена 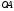 , то есть равной , то есть равной 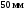 . Это означает, мы будем строить план скоростей в масштабе кривошипа. . Это означает, мы будем строить план скоростей в масштабе кривошипа.В этом случае масштабный коэффициент для построения плана скоростей определяется по формуле: 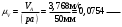 . .Затем находим скорость точки  . При плоском движении, которое совершает звено . При плоском движении, которое совершает звено 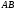 , согласно теореме о сложении скоростей, скорость точки , согласно теореме о сложении скоростей, скорость точки  определяется векторным уравнением: определяется векторным уравнением: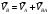 , ,где 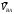 − вращательная скорость точки − вращательная скорость точки  вокруг полюса, которым является точка вокруг полюса, которым является точка  (за полюс т.А принимается та точка звена АВ, скорость которой известна). (за полюс т.А принимается та точка звена АВ, скорость которой известна).Так как согласно плану механизма точка  движется по горизонтальной направляющей, то вектор скорости точки движется по горизонтальной направляющей, то вектор скорости точки  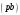 лежит на горизонтальной прямой. Началом вектора лежит на горизонтальной прямой. Началом вектора 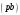 является полюс является полюс 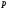 . Поэтому проводим из точки . Поэтому проводим из точки 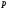 горизонтальную прямую. горизонтальную прямую.Вектор вращательной скорости точки  вокруг точки вокруг точки  , который обозначается , который обозначается 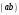 , перпендикулярен звену , перпендикулярен звену 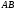 , так как: , так как: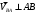 . .Для нахождения положения точки 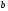 на плане скоростей, из точки на плане скоростей, из точки  проводим прямую перпендикулярную звену проводим прямую перпендикулярную звену 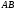 . Точка пересечения горизонтали, проведенной из точки . Точка пересечения горизонтали, проведенной из точки 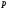 и прямой перпендикулярной звену и прямой перпендикулярной звену 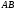 , проведенной из точки , проведенной из точки  , является точкой , является точкой 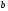 (рис. 2б). (рис. 2б).Скорость точки 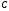 находится аналогично скорости точки находится аналогично скорости точки  : :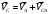 , ,где 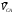 − вращательная скорость точки − вращательная скорость точки 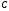 вокруг точки вокруг точки  . .Для построения вектора  , изображающего скорость точки , изображающего скорость точки  , делим вектор , делим вектор  пополам, так как точка пополам, так как точка  является серединой звена является серединой звена 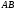 , и ставим точку , и ставим точку  . Затем из полюса . Затем из полюса 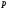 проводим вектор проводим вектор 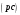 (рис. 2б). (рис. 2б).План скоростей построен. Определим согласно плану скоростей линейные скорости точек  и и 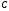 , а также угловую скорость звена , а также угловую скорость звена 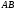 . .Измеряем на плане скоростей (рис. 2б) длины векторов 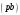 и и 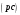 и и 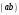 : :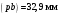 , , 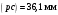 , , 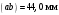 . .Используя масштабный коэффициент плана скоростей, находим требуемые скорости:  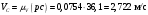 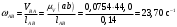 Направление угловой скорости 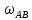 находится так. Мысленно переносим вектор находится так. Мысленно переносим вектор 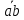 c плана скоростей в точку В на чертеж механизма и смотрим на направление поворота вектора c плана скоростей в точку В на чертеж механизма и смотрим на направление поворота вектора 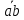 относительно точки А, это направление и будет направлением относительно точки А, это направление и будет направлением 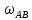 - угловой скорости звена АВ (рис. 2а). - угловой скорости звена АВ (рис. 2а).На этом первая часть задачи об определении угловых и линейных скоростей звеньев и точек механизма завершена. Рассмотрим, каким образом находятся ускорения механизма путем построения плана ускорений. Начинаем построение плана ускорений с ускорения точки  ведущего звена ведущего звена 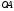 . Звено . Звено 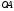 совершает равномерное вращательное движение, поэтому полное ускорение точки совершает равномерное вращательное движение, поэтому полное ускорение точки  равно нормальному ускорению равно нормальному ускорению 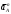 , поскольку , поскольку 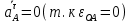 : :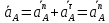 . Нормальное ускорение точки  найдем по формуле: найдем по формуле: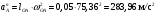 . .Ускорение 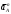 направлено вдоль звена направлено вдоль звена 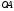 , от точки , от точки  к центру вращения, то есть к точке к центру вращения, то есть к точке 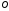 : :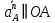 . .За полюс плана ускорений принимается произвольная точка, которую обозначают буквой  . Откладываем отрезок (a)параллельно звену . Откладываем отрезок (a)параллельно звену 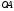 из произвольной точки из произвольной точки  . Длина отрезка (a) принимается произвольно, примем ее равной . Длина отрезка (a) принимается произвольно, примем ее равной 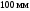 (рис. 2в). Тогда масштабный коэффициент плана ускорений определим по формуле: (рис. 2в). Тогда масштабный коэффициент плана ускорений определим по формуле: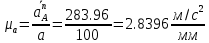 . .Ускорение точки  найдем согласно теореме о сложении ускорений при плоском движении: найдем согласно теореме о сложении ускорений при плоском движении: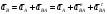 , ,(или как на плане ускорений 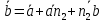 ) )где 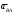 ( (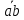 ) − ускорение точки ) − ускорение точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  ; ; ( (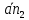 ) − нормальное ускорение точки ) − нормальное ускорение точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  ; ;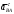 ( (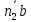 ) − касательное ускорение точки ) − касательное ускорение точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  . .Нормальное ускорение точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  будет направлено вдоль шатуна будет направлено вдоль шатуна 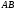 от точки от точки  к центру вращения, то есть к точке к центру вращения, то есть к точке  . Величину . Величину  найдем по формуле: найдем по формуле: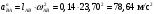 . .Отрезок ( 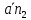 ), обозначающий нормальное ускорение точки ), обозначающий нормальное ускорение точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  , отложим от точки , отложим от точки  параллельно шатуну параллельно шатуну 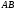 (рис. 2в). Длину отрезка ( (рис. 2в). Длину отрезка (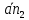 ) найдем по формуле: ) найдем по формуле: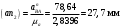 . .Величина касательного ускорения точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  нам неизвестна, но нам известны направления этого ускорения и полного ускорения точки нам неизвестна, но нам известны направления этого ускорения и полного ускорения точки  . Для определения положения точки . Для определения положения точки 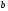 на плане ускорений отложим две прямые, вдоль которых направлены на плане ускорений отложим две прямые, вдоль которых направлены 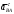 ( (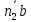 ) и ) и 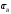 ( (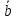 ). Точка ). Точка  движется по горизонтальной направляющей и совершает поступательное движение, поэтому полное ускорение движется по горизонтальной направляющей и совершает поступательное движение, поэтому полное ускорение 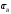 точки точки  направлено по горизонтали. Проводим из полюса направлено по горизонтали. Проводим из полюса  горизонтальную прямую. Касательное ускорение горизонтальную прямую. Касательное ускорение 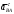 точки точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  направлено перпендикулярно шатуну направлено перпендикулярно шатуну 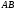 . Поэтому проводим прямую перпендикулярную . Поэтому проводим прямую перпендикулярную 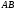 из точки из точки 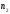 . На пересечении двух построенных прямых получаем точку . На пересечении двух построенных прямых получаем точку 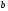 (рис. 2в). (рис. 2в).Отрезок ( 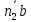 ) является касательным ускорением точки ) является касательным ускорением точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  , отрезок ( , отрезок (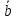 ) является полным ускорением точки ) является полным ускорением точки  (рис. 2в). (рис. 2в).Так как точка  является серединой звена является серединой звена  , то для нахождения положения точки c на плане ускорений, в середине отрезка ( , то для нахождения положения точки c на плане ускорений, в середине отрезка ( ), характеризующего полное ускорение точки ), характеризующего полное ускорение точки  во вращательном движении вокруг точки во вращательном движении вокруг точки  , ставим точку, обозначая её буквой c. Проводим отрезок ( , ставим точку, обозначая её буквой c. Проводим отрезок ( ), который является полным ускорением точки ), который является полным ускорением точки 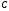 (рис. 2в). (рис. 2в).План ускорений построен. Найдем искомые величины ускорений. Измеряем на плане ускорений длины векторов ( 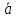 ), ( ), (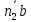 ), ( ), (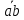 ), ( ), (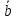 ), ( ), (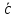 ): ): 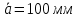 , , 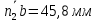 , ,  , ,  , ,  Используя масштабный коэффициент плана ускорений, находим требуемые ускорения:  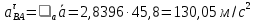 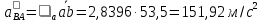 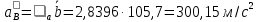 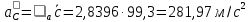 Найдем величину и направление углового ускорения звена 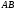 : :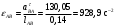 . .Мысленно поместив вектор 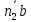 в точку в точку  механизма (рис. 2а), видим, что угловое ускорение механизма (рис. 2а), видим, что угловое ускорение 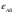 звена звена 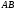 относительно точки А направлено против хода часовой стрелки. относительно точки А направлено против хода часовой стрелки.После определения скоростей и ускорений кинематический анализ механизма считается завершенным. Перейдем ко второй части задачи, в которой необходимо выполнить силовой анализ механизма. ) Силовой анализ механизма Силовой анализ механизма основывается на решении первой (прямой) задачи динамики – по заданному движению определить действующие силы. При силовом анализе механизма законы движения его звеньев должны быть известны, то есть кинематический анализ механизма должен быть завершен, что было сделано нами выше. Кроме того, должны быть заданы внешние силы, действующие на механизм. То есть, при силовом анализе механизма должны быть определены силы инерции и реакции в кинематических парах. Однако встречаются задачи силового анализа, в которых внешние силы, приложенные к ведущим звеньям, являются неизвестными. В таких случаях необходимо найти еще и эти неизвестные силы. При силовом анализе механизмов используется принцип Даламбера, согласно которому звено механизма рассматривается находящимся в равновесии, при условии прикладывания к нему наряду с внешними силами сил инерции в зависимости от вида движения звена. Силовой анализ механизма начнем с построения плана механизма в заданном положении с учетом определенных ранее скоростей и ускорений звеньев механизма (рис 3а). На этот раз для построения плана механизма воспользуемся не чертежным масштабом, а масштабным коэффициентом. Примем длину ведущего звена 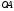 на плане равной на плане равной 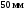 . Тогда масштабный коэффициент для плана механизма: . Тогда масштабный коэффициент для плана механизма: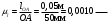 . .Для удобства дальнейших построений сил инерции на рис. 3 поместим план ускорений, который был построен нами ранее (рис. 3б). Определяем силы инерции, действующие на звенья механизма по следующим формулам: 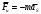 , , 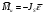 , ,где 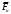 − главный вектор сил инерции звена (сила инерции); − главный вектор сил инерции звена (сила инерции);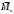 − главный момент от сил инерции звена (момент пары сил инерции); − главный момент от сил инерции звена (момент пары сил инерции);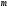 − масса звена; − масса звена;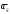 − ускорение центра масс звена; − ускорение центра масс звена;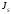 − момент инерции звена относительно оси, проходящей через центр масс; − момент инерции звена относительно оси, проходящей через центр масс;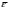 − угловое ускорение звена. − угловое ускорение звена.Для удобства маркировки сил инерции обозначим кривошип 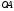 цифрой цифрой 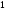 , шатун , шатун 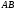 цифрой цифрой 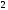 , ползун , ползун  цифрой цифрой 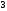 . Тогда силы инерции, ускорения, угловые ускорения, массы и моменты инерции каждого звена будем обозначать, используя присвоенные звеньям цифровые индексы. Кроме того центр масс первого звена обозначим . Тогда силы инерции, ускорения, угловые ускорения, массы и моменты инерции каждого звена будем обозначать, используя присвоенные звеньям цифровые индексы. Кроме того центр масс первого звена обозначим 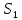 расположенный в точке О. Центр масс второго звена в задаче обозначен расположенный в точке О. Центр масс второго звена в задаче обозначен 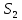 и расположен в точке и расположен в точке 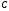 , и его ускорение мы вычислили выше. , и его ускорение мы вычислили выше.Находим величины сил инерции для каждого звена: Звено АВ (2ое) – движение плоское 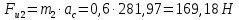 ; ;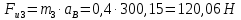 ; ;Для нахождения момента от сил инерции 2ого звена (АВ), необходимо знать момент инерции этого звена относительно оси, проходящей через их центр масс т.С. Поскольку звено 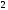 по условию задачи являются тонкими однородными стержнями с постоянным поперечным сечением, то момент инерции определяются по формуле: по условию задачи являются тонкими однородными стержнями с постоянным поперечным сечением, то момент инерции определяются по формуле: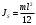 . .Тогда момент сил инерции 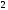 звена: звена: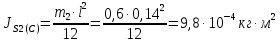 ; ;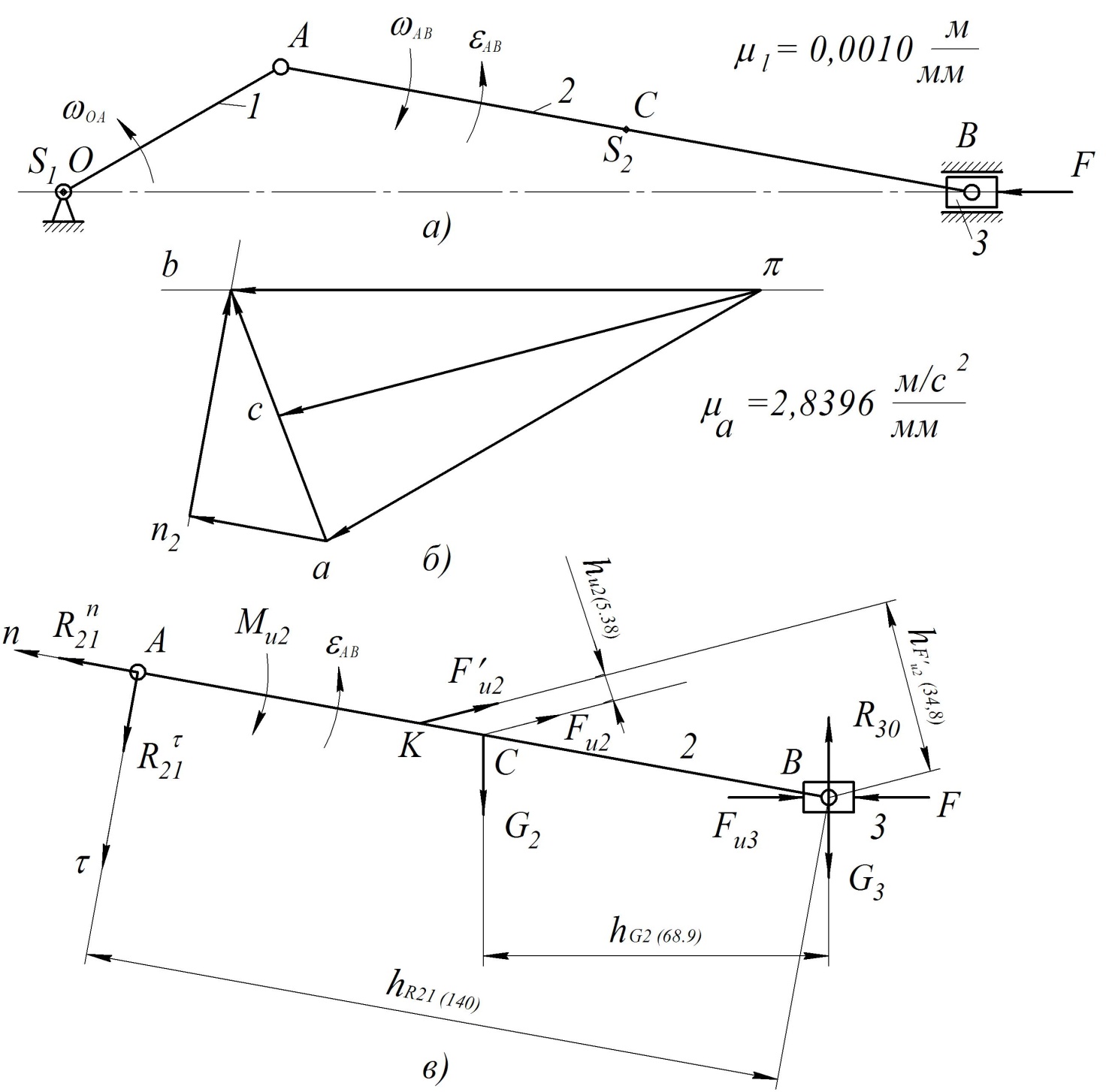 Рисунок 3. Силовой анализ звеньев 2 и 3 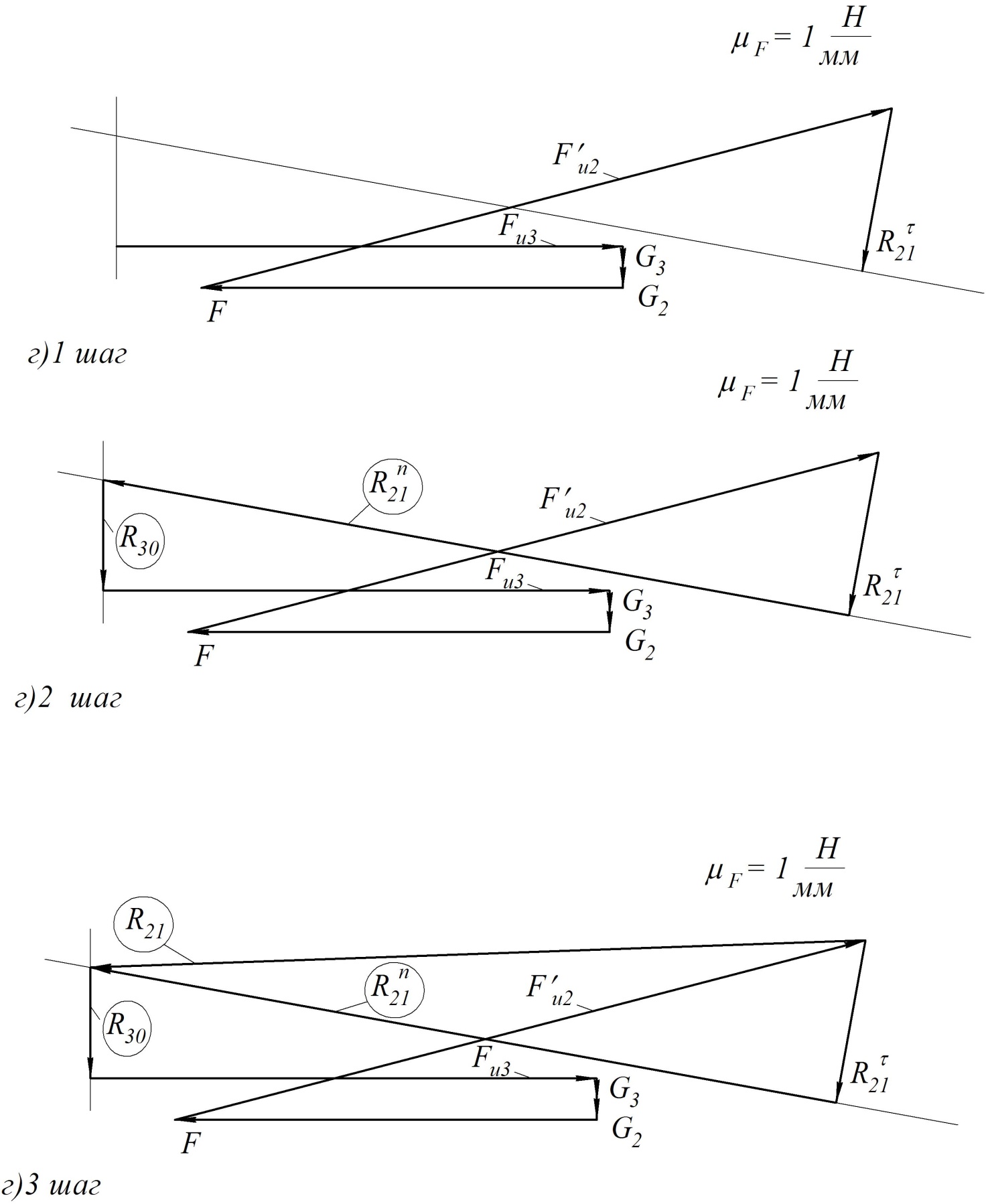 Рисунок 3. Силовой анализ звеньев 2 и 3 Находим величину момента от сил инерции: 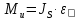 : :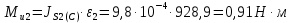 Силовой анализ механизма необходимо начинать со звеньев, наиболее удаленных от ведущего звена. Поэтому в выбранном масштабе ( 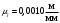 ) строим звенья ) строим звенья 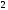 и и 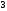 , прикладывая к ним все действующие силы (рис. 3в). , прикладывая к ним все действующие силы (рис. 3в). На рисунке 3в указаны следующие силы: 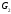 и и 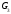 − силы тяжести соответственно второго и третьего звеньев (направлены вертикально вниз); − силы тяжести соответственно второго и третьего звеньев (направлены вертикально вниз); 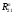 − нормальная составляющая реакции в шарнире − нормальная составляющая реакции в шарнире  со стороны второго звена на первое звено (направлена параллельно звену 2 в произвольную сторону); со стороны второго звена на первое звено (направлена параллельно звену 2 в произвольную сторону); 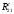 − касательная составляющая реакции в шарнире − касательная составляющая реакции в шарнире  со стороны второго звена на первое звено (направлена перпендикулярно звену 2 в произвольную сторону); со стороны второго звена на первое звено (направлена перпендикулярно звену 2 в произвольную сторону); 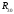 − нормальная реакция опоры в точке − нормальная реакция опоры в точке  (направлена перпендикулярно направляющей); (направлена перпендикулярно направляющей); 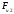 − сила инерции второго звена (приложена в центре масс второго звена, направлена противоположно ускорению − сила инерции второго звена (приложена в центре масс второго звена, направлена противоположно ускорению 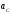 центра масс); центра масс); 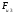 − сила инерции третьего звена (приложена в центре масс третьего звена, направлена противоположно ускорению − сила инерции третьего звена (приложена в центре масс третьего звена, направлена противоположно ускорению 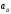 ); ); 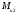 − момент от сил инерции второго звена (приложен ко второму звену, направлен противоположно угловому ускорению − момент от сил инерции второго звена (приложен ко второму звену, направлен противоположно угловому ускорению 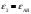 ); ); 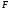 − внешняя сила полезного сопротивления. − внешняя сила полезного сопротивления.Для построения силового многоугольника к звену должны быть приложены только сосредоточенные силы, поэтому моменты от сил инерции, действующие на звенья механизмов, заменяют результирующими силами. В нашей задаче необходимо силу инерции 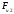 и момент от сил инерции и момент от сил инерции 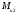 заменить одной результирующей силой заменить одной результирующей силой 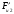 . Для этого необходимо вычислить плечо, на которое сила . Для этого необходимо вычислить плечо, на которое сила 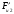 переносится из центра масс звена: переносится из центра масс звена: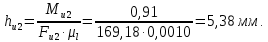 Прикладываем силу 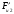 к звену 2 параллельно силе к звену 2 параллельно силе 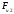 в точку в точку 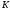 , отстоящую от центра масс второго звена на плечо , отстоящую от центра масс второго звена на плечо 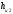 . Точка . Точка 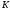 выбирается так, чтобы момент, который создает сила выбирается так, чтобы момент, который создает сила 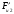 относительно центра масс звена, совпадал по направлению с моментом относительно центра масс звена, совпадал по направлению с моментом 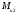 (рис. 3в). (рис. 3в).Для определения касательной составляющей реакции 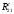 в шарнире в шарнире  составим уравнение моментов всех сил, относительно точки составим уравнение моментов всех сил, относительно точки  : :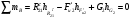 . .Из полученного уравнения выражаем и вычисляем 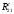 , взяв плечи каждой из сил, входящей в уравнение с чертежа (рис. 3в), и подставив их в , взяв плечи каждой из сил, входящей в уравнение с чертежа (рис. 3в), и подставив их в  : :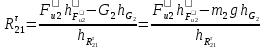 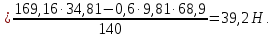 Величина 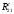 получилась положительной. Это означает, что направление данной силы на рисунке 3в показано верно. Если бы сила получилась с отрицательным знаком, то её направление необходимо было бы поменять на противоположное. получилась положительной. Это означает, что направление данной силы на рисунке 3в показано верно. Если бы сила получилась с отрицательным знаком, то её направление необходимо было бы поменять на противоположное.Для определения неизвестных реакций 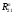 и и 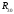 , для которых известны только линии действия, составляем векторное уравнение равновесия звеньев , для которых известны только линии действия, составляем векторное уравнение равновесия звеньев 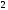 и и 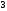 : :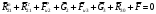 . .По полученному векторному уравнению равновесия строим силовой многоугольник, называемый планом сил. Направления и величины всех сил, кроме 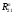 и и 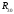 , входящих в векторное уравнение равновесия нам известны. Шаг 1. Построение силового многоугольника можно начинать с любой из известных сил, прикладывая в конец вектора первой из построенных сил, следующую известную силу. Примем масштабный коэффициент для плана сил , входящих в векторное уравнение равновесия нам известны. Шаг 1. Построение силового многоугольника можно начинать с любой из известных сил, прикладывая в конец вектора первой из построенных сил, следующую известную силу. Примем масштабный коэффициент для плана сил 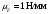 . Для определения длины вектора, обозначающего силу на плане сил, необходимо числовое значение силы поделить на масштабный коэффициент. . Для определения длины вектора, обозначающего силу на плане сил, необходимо числовое значение силы поделить на масштабный коэффициент.Показанный на рисунке 3г силовой многоугольник строился в последовательности: 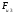 , , 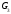 , , 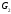 , , 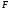 , , 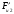 , , 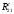 . .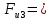 120,06 Н; 120,06 Н; 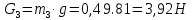 ; ; 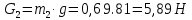 ; ; 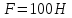 ; ; 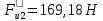 ; ; 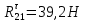 . .Шаг 2. Поскольку рассматриваемые звенья под действием приложенных к ним сил рассматриваются как находящиеся в равновесии, то силовой многоугольник должен быть замкнутым. Для замыкания силового многоугольника необходимо достроить неизвестные реакции 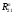 и и 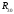 . Делаем это следующим образом. Из конца вектора, обозначающего реакцию . Делаем это следующим образом. Из конца вектора, обозначающего реакцию 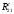 , проводим прямую, параллельную линии действия реакции , проводим прямую, параллельную линии действия реакции 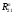 . Из начала вектора, обозначающего силу . Из начала вектора, обозначающего силу 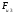 , проводим прямую параллельную линии действия реакции , проводим прямую параллельную линии действия реакции 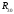 . Точка пересечения проведенных прямых является концом вектора, обозначающего реакцию . Точка пересечения проведенных прямых является концом вектора, обозначающего реакцию 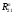 , и началом вектора, обозначающего реакцию , и началом вектора, обозначающего реакцию 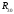 . Замыкаем силовой многоугольник достроив недостающие векторы. Шаг 3. Проведя вектор из начала . Замыкаем силовой многоугольник достроив недостающие векторы. Шаг 3. Проведя вектор из начала 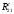 в конец в конец 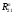 , получим вектор результирующей реакции , получим вектор результирующей реакции 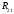 . .Измерив на плане сил длины векторов, обозначающих реакции 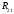 , , 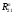 , , 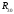 , и умножив их на , и умножив их на 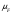 , получаем значения неизвестных реакций: , получаем значения неизвестных реакций: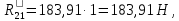 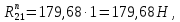 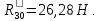 В задаче осталось найти реакцию шарнира 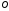 . Для этого необходимо рассмотреть равновесие звена . Для этого необходимо рассмотреть равновесие звена 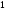 . Последовательность действий должна быть такой же, которая проводилась при силовом анализе звеньев . Последовательность действий должна быть такой же, которая проводилась при силовом анализе звеньев  и и  . Все графические построения, сопутствующие силовому анализу механизма удобно проводить на одном листе бумаги. Но так как формат листа А4 довольно мал по размерам для подобных построений, то силовой анализ звена . Все графические построения, сопутствующие силовому анализу механизма удобно проводить на одном листе бумаги. Но так как формат листа А4 довольно мал по размерам для подобных построений, то силовой анализ звена  проведем на отдельном листе, перенеся на него с рисунка 3 план механизма (рис. 4а), план ускорений (рис. 4б), указав на плане механизма направление найденной выше реакции проведем на отдельном листе, перенеся на него с рисунка 3 план механизма (рис. 4а), план ускорений (рис. 4б), указав на плане механизма направление найденной выше реакции  в шарнире в шарнире  . . Звено 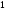 построим длиной построим длиной 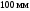 , тогда для него масштабный коэффициент: , тогда для него масштабный коэффициент: 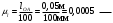 . .Прикладываем к звену 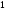 , действующие на него силы (рис. 4в). На рисунке 4в указаны следующие силы: , действующие на него силы (рис. 4в). На рисунке 4в указаны следующие силы: 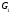 − сила тяжести (направлена вертикально вниз), приложена в точке О; − сила тяжести (направлена вертикально вниз), приложена в точке О; 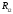 − реакции в шарнире − реакции в шарнире  со стороны первого звена на второе звено (направлена в противоположную сторону реакции со стороны первого звена на второе звено (направлена в противоположную сторону реакции 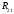 и равна ей по величине); и равна ей по величине); 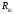 − реакция в шарнире − реакция в шарнире 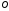 (направлена произвольно); (направлена произвольно);  . ‑ уравновешивающая сила приложена в точке А и направлена перпендикулярно звену ОА в сторону противоположную направлению момента от силы . ‑ уравновешивающая сила приложена в точке А и направлена перпендикулярно звену ОА в сторону противоположную направлению момента от силы  . .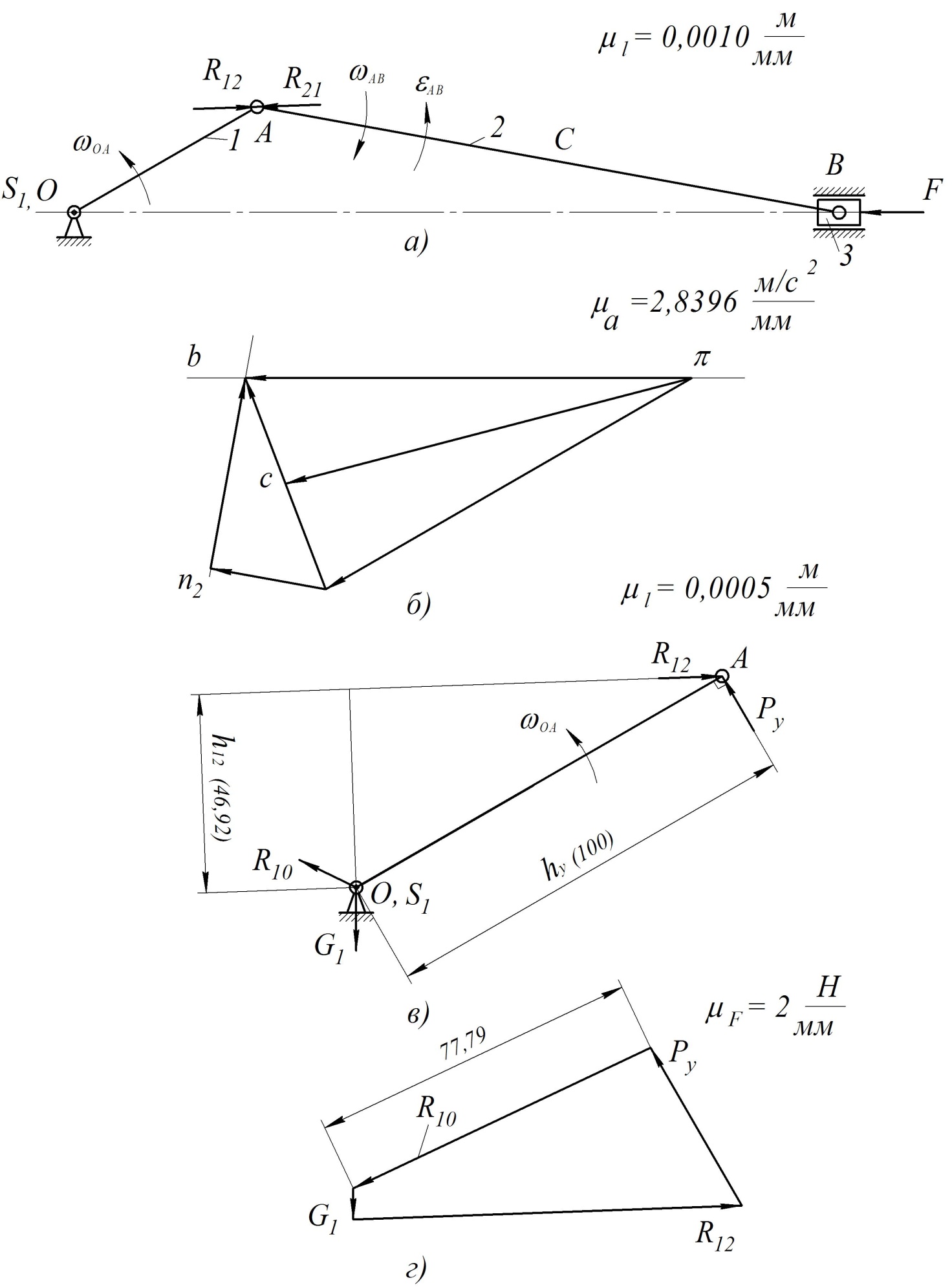 Рисунок 4. Силовой анализ звена 1 Для определения неизвестной реакций 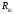 составляем векторное уравнение равновесия звена составляем векторное уравнение равновесия звена 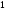 : :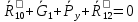 По полученному векторному уравнению равновесия строим план сил. В уравнении неизвестны силы 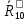 и и 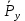 . Силу реакции опоры найдем графически, а . Силу реакции опоры найдем графически, а 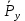 .‑ уравновешивающую силу, вычислим из уравнения моментов сил действующих на звено, составленное относительно точки О: .‑ уравновешивающую силу, вычислим из уравнения моментов сил действующих на звено, составленное относительно точки О: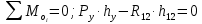 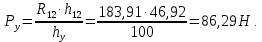 Примем масштабный коэффициент для плана сил 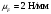 . Для определения длины вектора, обозначающего силу на плане сил, необходимо числовое значение силы поделить на масштабный коэффициент. . Для определения длины вектора, обозначающего силу на плане сил, необходимо числовое значение силы поделить на масштабный коэффициент. Показанный на рисунке 4г силовой многоугольник строился в последовательности: 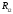 , ,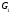 , ,  ., ., где 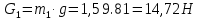 . .Поскольку рассматриваемые звенья под действием приложенных к ним сил рассматриваются как находящиеся в равновесии, то силовой многоугольник должен быть замкнутым. Для замыкания силового многоугольника необходимо достроить неизвестную реакцию  . Делаем это следующим образом. Конец вектора, обозначающего силу . Делаем это следующим образом. Конец вектора, обозначающего силу  . соединяем с началом вектора, обозначающего реакцию . соединяем с началом вектора, обозначающего реакцию  . Полученный отрезок является ничем иным, как неизвестной реакцией . Полученный отрезок является ничем иным, как неизвестной реакцией  . .Измерив на плане сил длину вектора, обозначающего реакцию 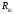 , и умножив её на , и умножив её на 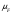 , получаем значение неизвестной реакций: , получаем значение неизвестной реакций: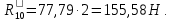 На этом все расчеты, заключенные в рамки курсовой работы завершены. При оформлении курсовой работы все построения размещаем на одном листе формата А2. |
