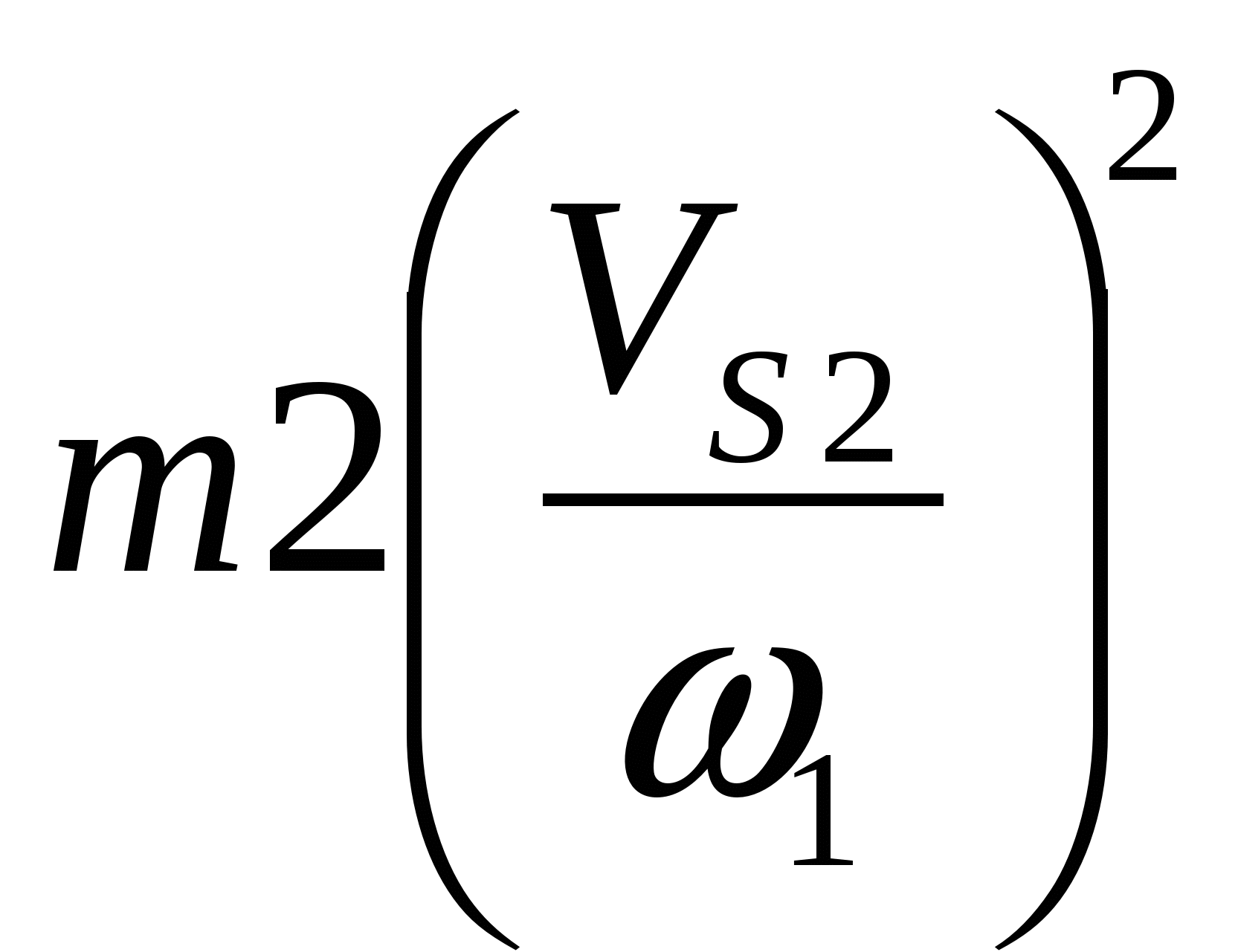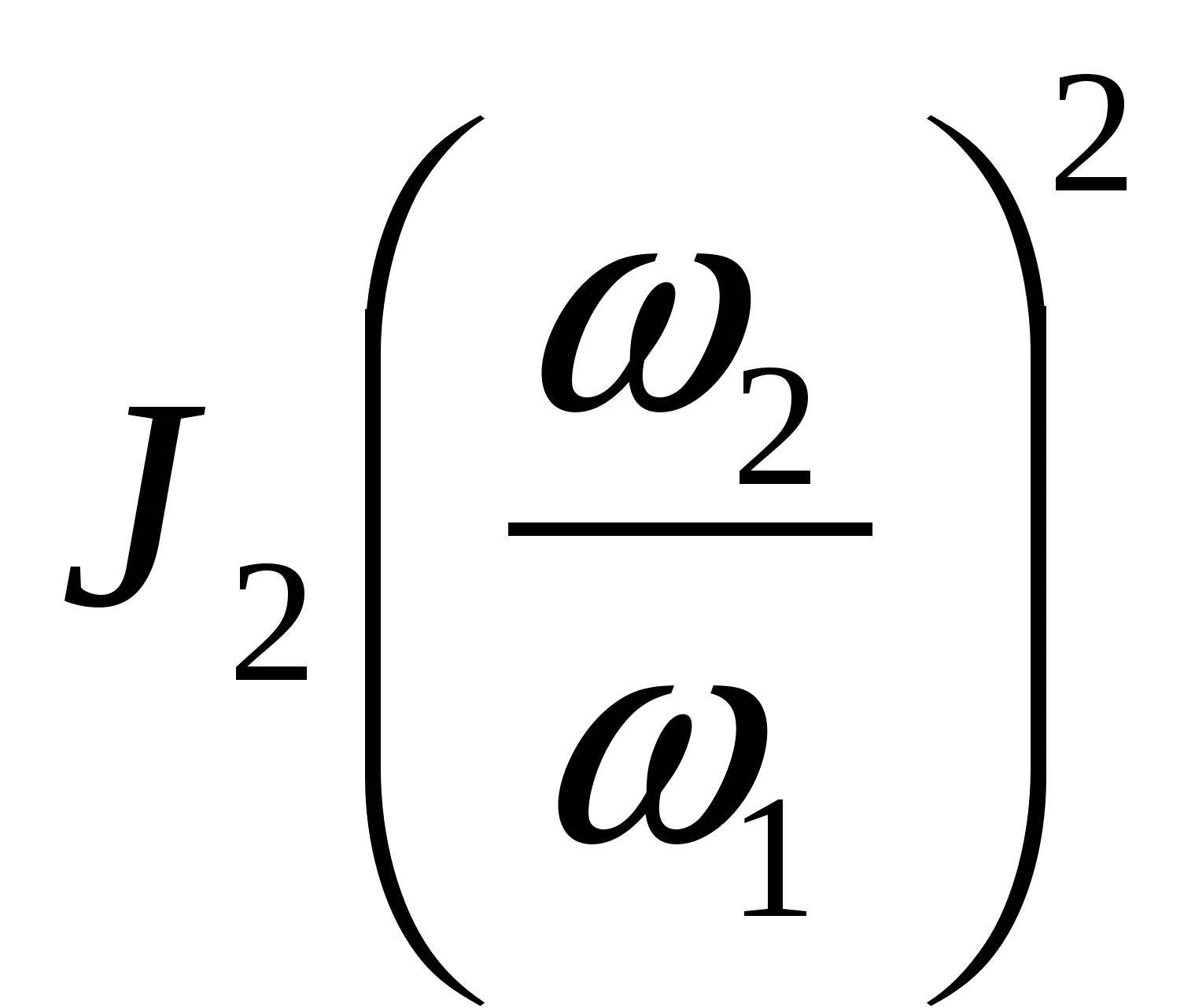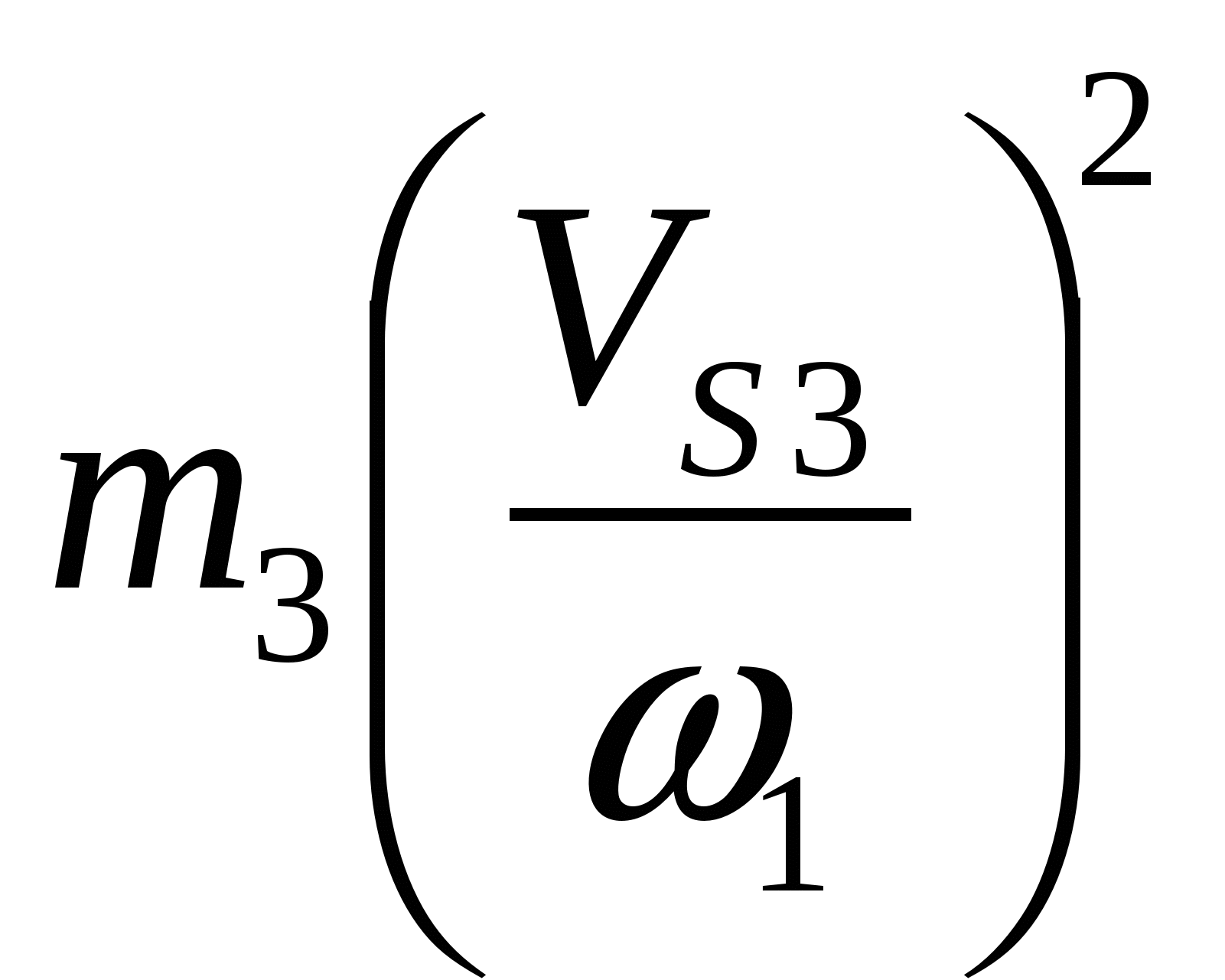Кинематический анализ механизма

Название	Кинематический анализ механизма
Дата	09.11.2018
Размер	1.87 Mb.
Формат файла
Имя файла	kontr_tmm.doc
Тип	Исследование #55953
страница	3 из 3

1 2 3

3. Расчет маховика.

^{Так как внутри цикла установившегося движения машин не наблюдается равенства движущих сил и работы сил сопротивления и постоянства приведённого момента инерции механизма, то угловая скорость  ведущего звена оказывается переменной. Величина колебаний скорости оценивается коэффициентом неравномерности хода.}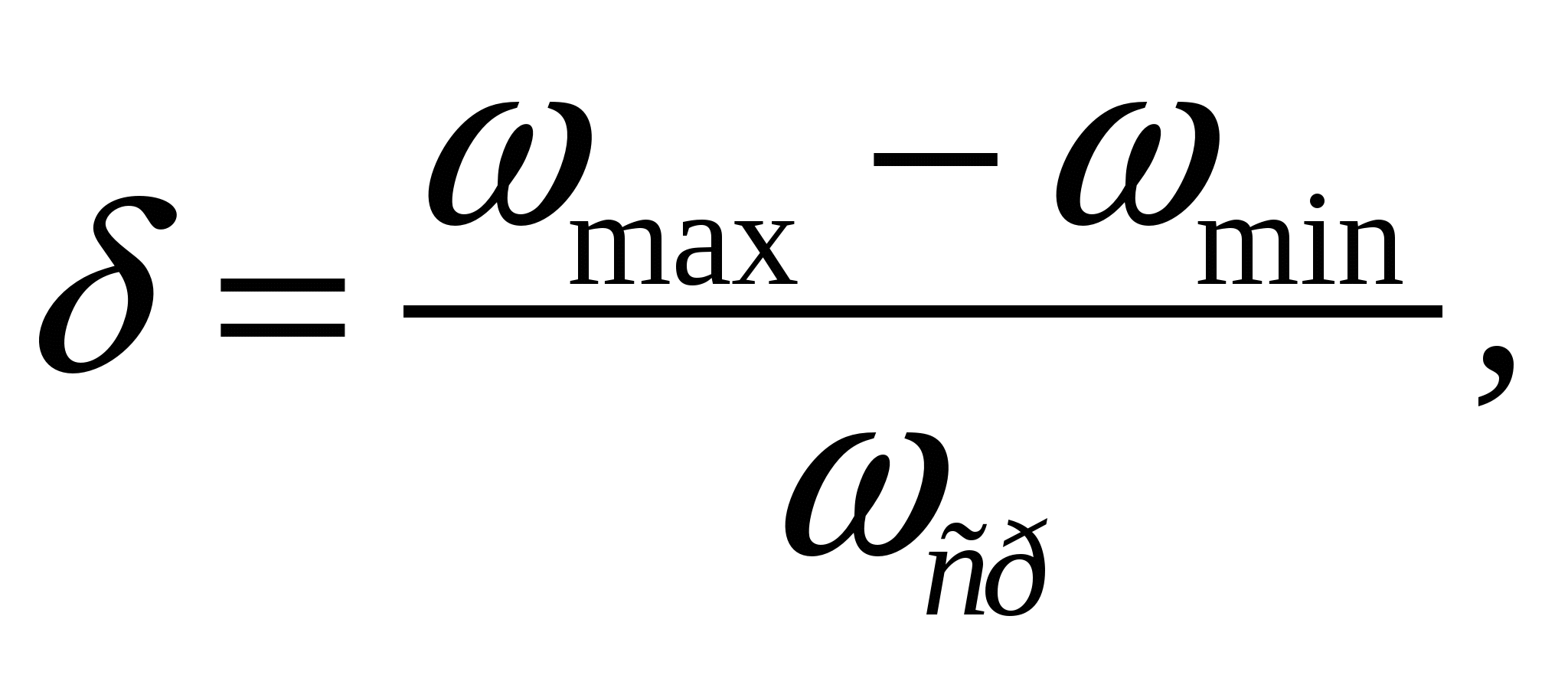

^{где мах - максимальная угловая скорость;}

^{min - минимальная угловая скорость;}

^{ср - средняя угловая скорость.}

^{За среднюю угловую скорость можно принять номинальную скорость}

^{Колебания скорости начального звена механизма должны регулироваться в заранее заданных пределах. Это регулирование обычно выполняется соответствующим побором масс звеньев механизма. Массы звеньев механизма должны побираться так, чтобы они могли накапливать все приращения кинетической энергии при превышении работы движущих сил над работой сил сопротивления и отдавать кинетическую энергию, когда работа сил сопротивления будет превышать работу движущих сил.}

^{Роль аккумулятора кинетической энергии механизма обычно выполняет маховик. Основной задачей расчёта является подобрать массу маховика, такой, что механизм мог осуществлять работу с заданным коэффициентом неравномерности движения =1/11.}

^{Для расчёта маховика используем метод энергомасс. По этому методу момент инерции маховика определяется по диаграмме энергомасс, характеризующей зависимость приращения кинетической энергии механизма от приведённого момента инерции механизма.}

^{Так как приращение кинетической энергии равно разности работы движущих сил и работы сил сопротивления, то для построения этой диаграммы необходимо построить вначале диаграммы приведённых моментов движущих сил и сил сопротивления.}

^{Приведённый к ведущему звену момент сил производственного сопротивления для каждого положения исследуемого механизма определяется по формуле:}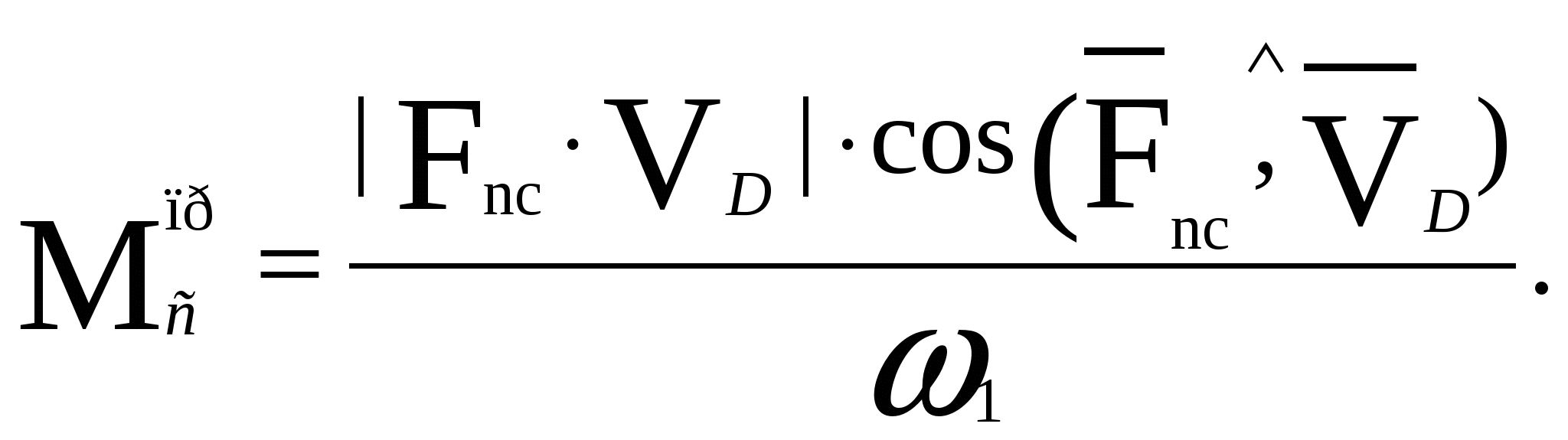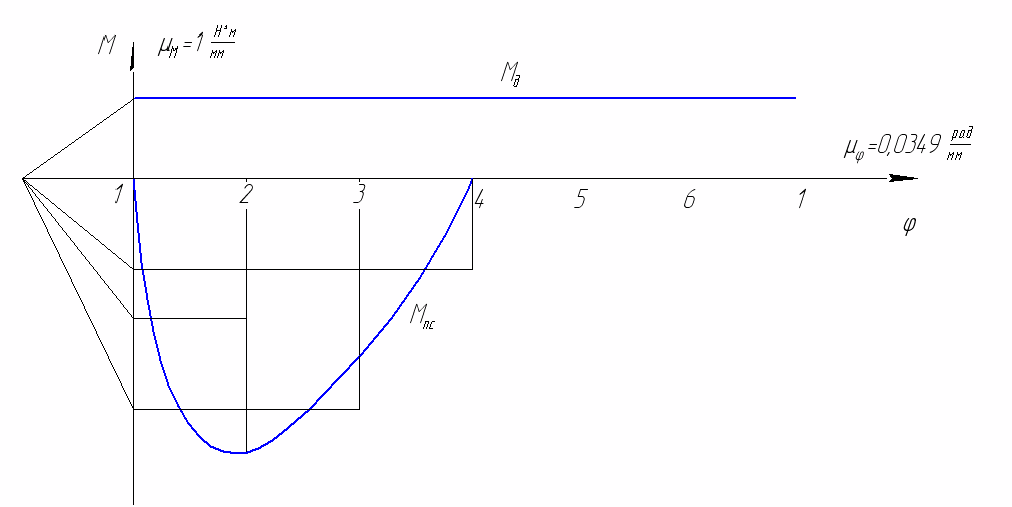

^.

^{Расчёт приведённого момента сил производственных сопротивлений для всех положений занесём в таблицу 8.}

^{Таблица 8}

^{Расчёт приведённого момента сил сопротивлений.}

	1	2	3	4	5	6
Fп, Н	200	200	100	100	0	0
Vd	0	19,45	25,2	0	26,3	20,5
MПС	0	-74,3359	-48,1559	0	0	0
Y	0	-74,3359	-48,1559	0	0	0
масштабный коэффициент		1	Н*м/мм

^{На основании данных таблицы построим график изменения сил производственных сопротивлений МП.С. от функции угла поворота начального звена. Масштаб по оси Mпвыбираем равным 1 Нм/мм, масштаб по оси абсцисс при длине диаграммы l=180 мм составит 0,0349 рад/мм.}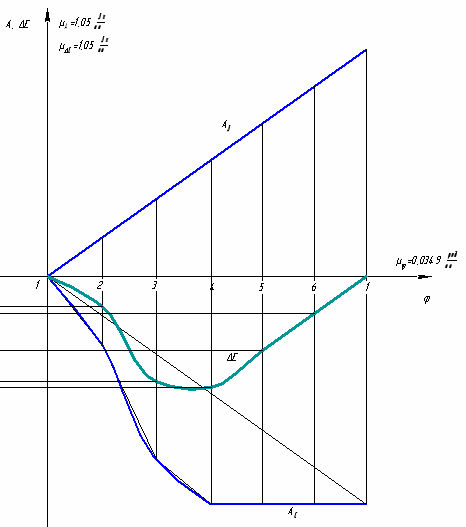

^{Так как работа сил производственных сопротивлений равна:}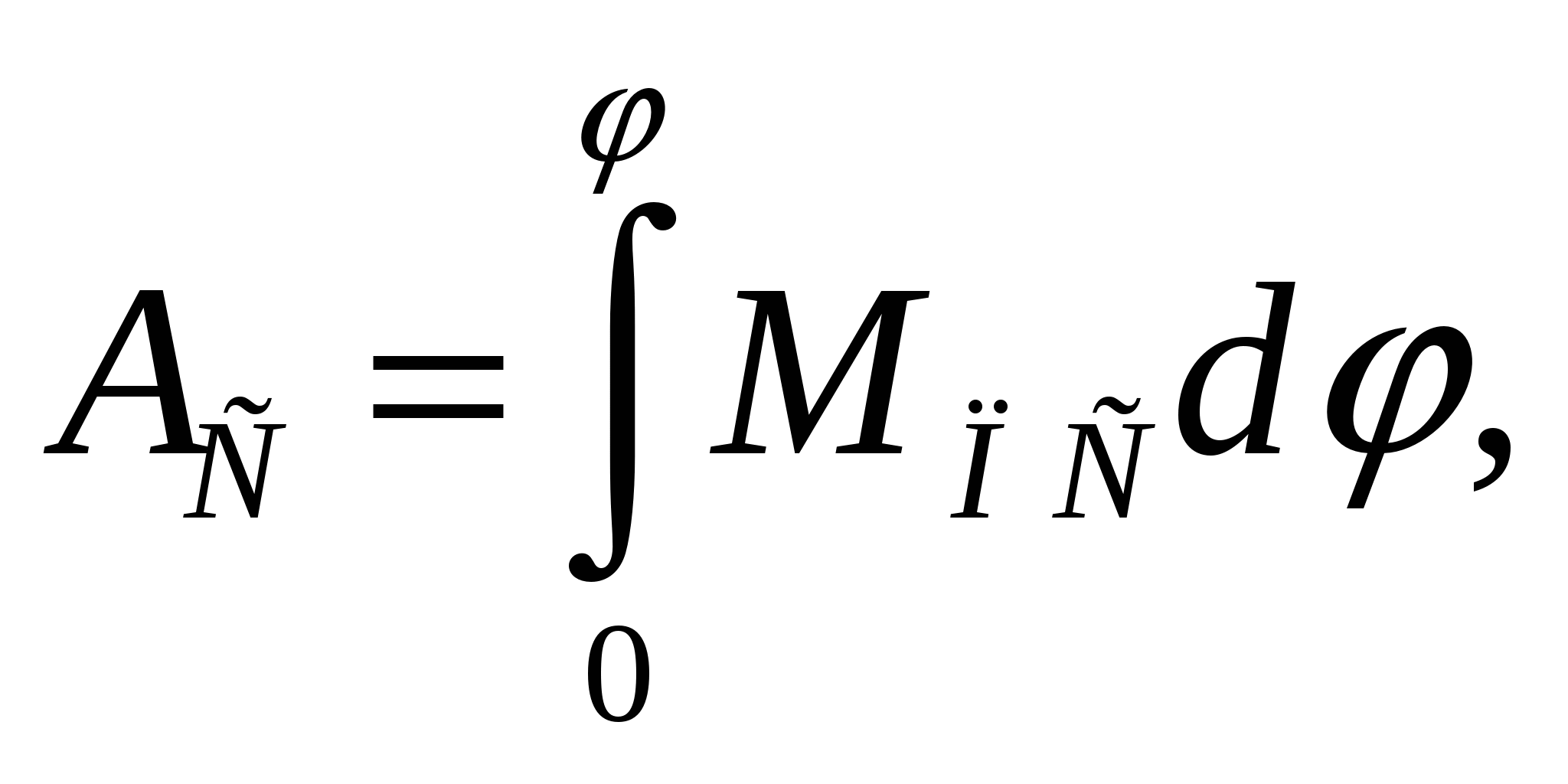

^{то графическим интегрированием приведённых моментов сил производственных сопротивлений строим диаграмму работ сил производственных сопротивлений. Масштаб по оси ординат определим по формуле:}

^{где Н - полюсное расстояние.}

^{За один цикл установившегося движения (один оборот ведущего звена) работа сил производственных сопротивлений равна работе движущих сил.}

^{Примем постоянным момент работы движущих сил. Тогда работа движущих сил будет равна:}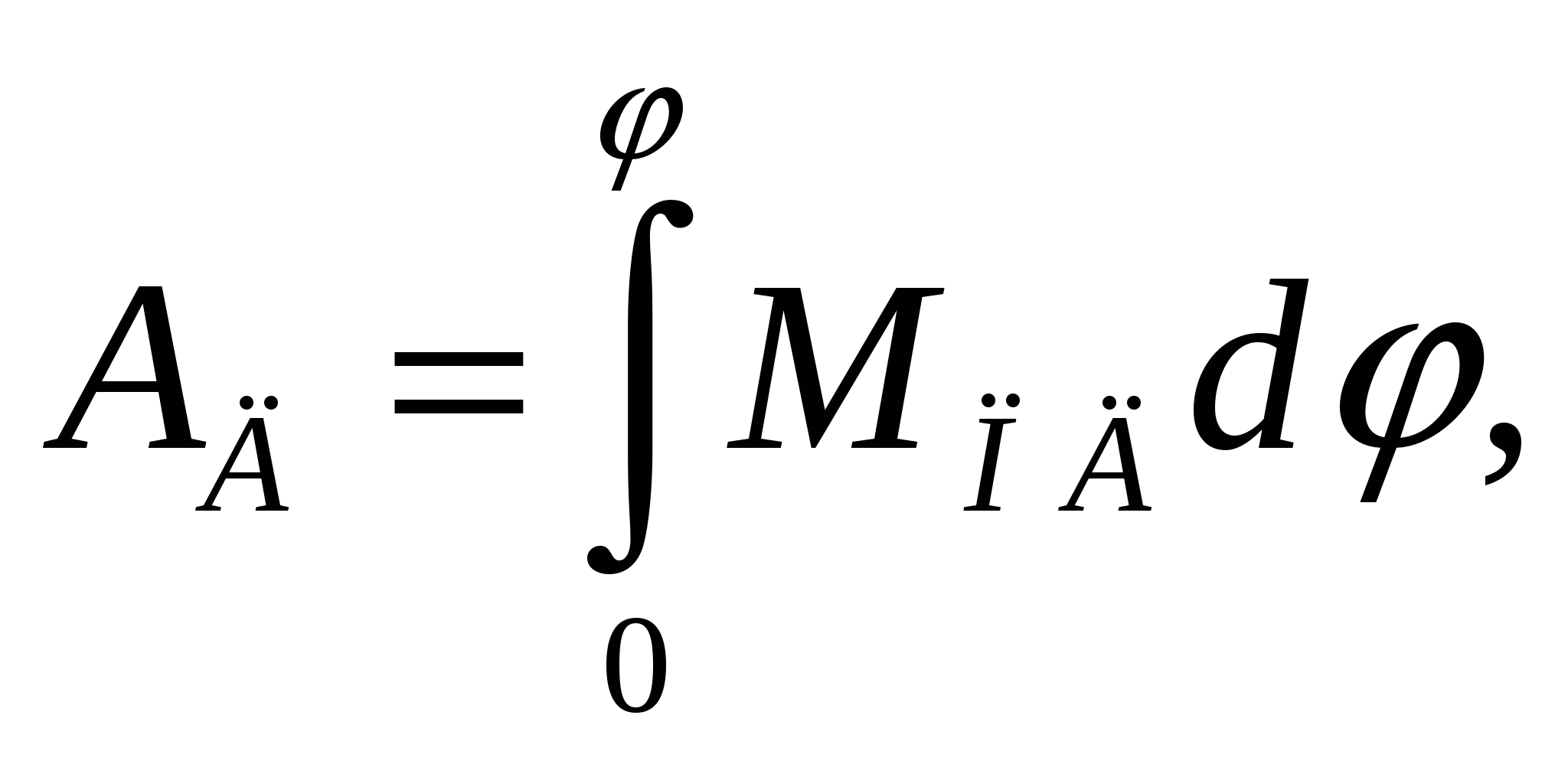

^{т.е. представляет собой линейную функцию угла поворота ведущего звена. Соединив начало координат с последней точкой диаграммы работ сил производственных сопротивлений, получим наклонную прямую – диаграмму работы движущих сил. Продифференцировав графически полученную прямую на диаграмме приведённых моментов, получим горизонтальную прямую, представляющую собой величину постоянного приведённого момента движущих сил.}

^{Так как приращение кинетической энергии равно:}

^{то для построения диаграммы изменения энергии или избыточной работы необходимо из ординаты диаграммы работы движущих сил вычесть ординату работы сил сопротивления.}

^{Масштабы по координатным осям остаются теми же, что и для диаграммы работ.}

^{Определим приведённый момент инерции маховика.}

^{Для звена, совершающего поступательное движение (ползун), кинетическая энергия равна:}

,

^{где m - масса звена;}

^{V - скорость поступательного движения.}

^{Для звена, совершающего вращательное движение (кривошип), кинетическая энергия равна:}

^{где J - момент инерции относительно оси инерции;}

^{ - угловая скорость звена.}

^{Кинетическая энергия звена, совершающего сложное движение, равна сумме кинетических энергий поступательного и вращательного движений.}

^{где Vs - скорость центра масс;}

^{Js - момент инерции звена относительно оси проходящей через центр масс.}

^{Складывая кинетические энергии звеньев, получим кинетическую энергию механизма.}

В нашем примере полная кинетическая энергия механизма: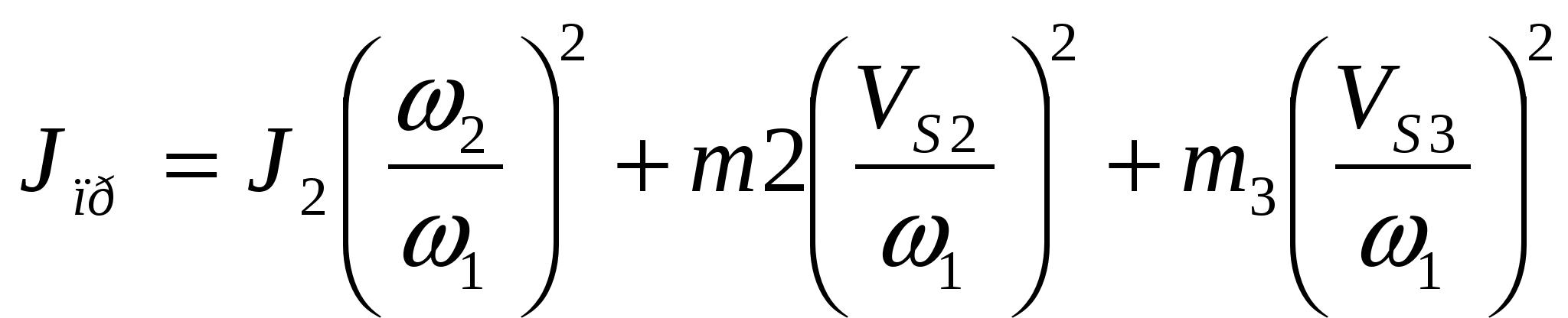

_Откуда

Массы звеньев берем следующие: кривошипа

кг,

кг.

Момент инерции второго звена

кг*м².

Вычисления приведённого момента приведём в таблице 9.

^{По данным таблицы строим диаграмму приведённых моментов инерции механизма в функции угла поворота начального звена. Принимаем масштаб μjp=0,1 кгм2/мм.}

^{Методом исключения параметра φ из диаграмм ΔЕК = ΔЕК (φ) и Jп=Jп(φ) строим диаграмму энергомасс ΔЕК=ΔЕК (Jп).}

^{Таблица 9.}

^{Расчёт приведённого момента инерции}

	1	2	3	4	5	6
	1,880019598	5,134943	6,929402	1,88002	6,819631	5,745009
	0,626673199	0,232252	0,104522	0,626673	0,241071	0,105501
	0	2,072187	3,478491	0	3,788797	2,301959
Jпр	2,506692797	7,439382	10,51241	2,506693	10,8495	8,152469
Y	25,06692797	74,39382	105,1241	25,06693	108,495	81,52469
масштабный коэффициент		0,1
m2	30
m3	15
Js2	10

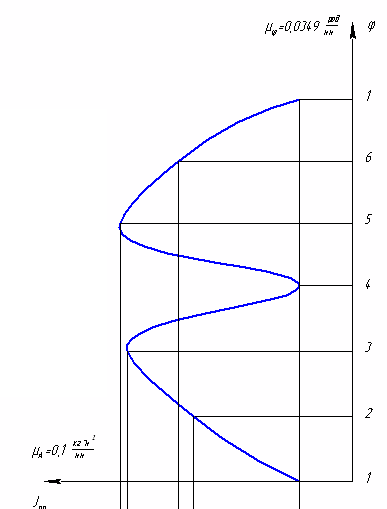^{Совмещаем графики изменения кинетической энергии и приведенного момента инерции звеньев. Получаем тем самым кривую энергомасс.}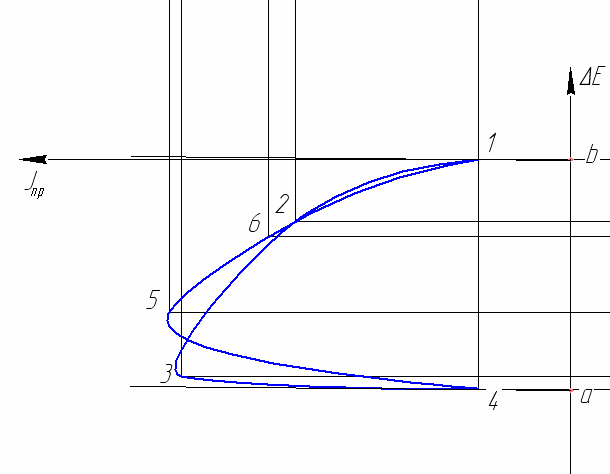

^{По данному коэффициенту неравномерности движения δ=1/11 и средней угловой скорости ωср =52,33 рад/с, определим углы ψmах и ψmin, образуемые касательными к диаграмме энергомасс с осью абсцисс:}

^,

^,

^.

Построив стороны этих углов и перенеся их параллельно самим себе до момента касания с кривой энергомасс, соответственно сверху и снизу, получим на оси ∆Ек отрезок mn=87,1 мм, заключённый между этими касательными.

Из отрезка mn определяем момент инерции маховика.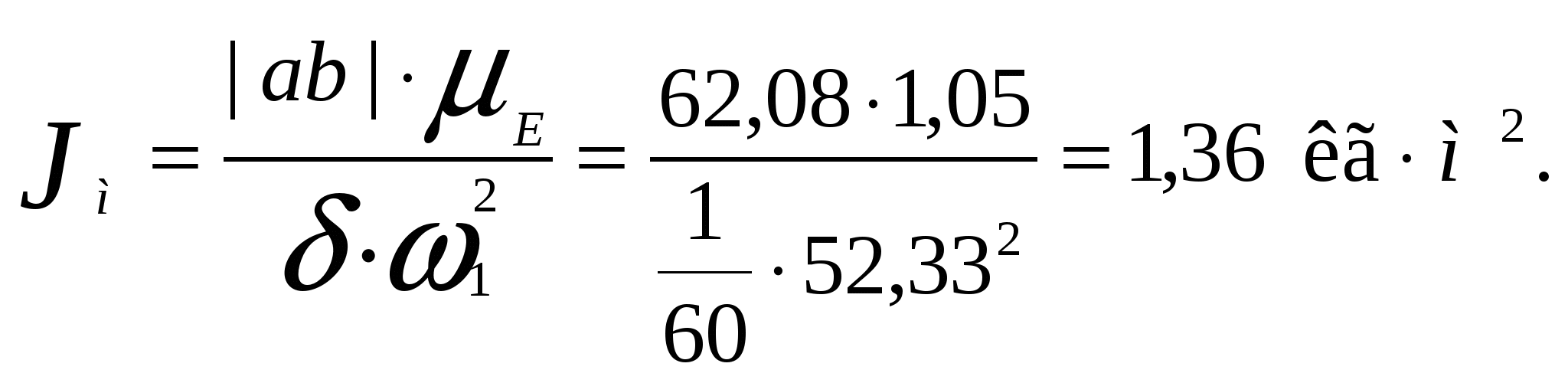

Диаметр маховика со спицами определяется зависимостью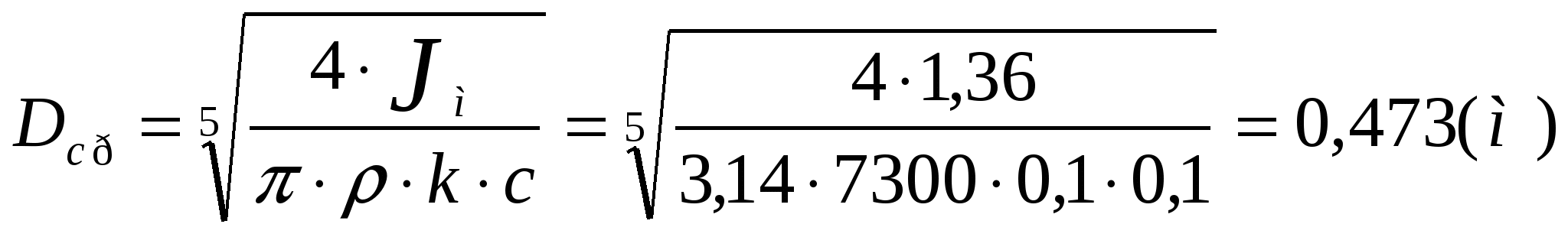

где

- отношение толщины обода H к его среднему диаметру.

Вычислим массу маховика. Для маховика со спицами:

кг.

4. Синтез кулачкового механизма.

4.1. Определение минимального радиуса кулачка R_min
1) Строим графики

.

Вычисляем масштаб

. По оси φ откладываем отрезок (0 - 8), равный 45 мм и соответствующий углу

= 45°. Тогда

Теперь уже в этом масштабе откладываем отрезок (8—8’), равный 100 мм, соответствующий углу

, за тем откладываем отрезок (8’-16), равный 60 мм, соответствующий углу

= 60°.

2) Строим совмещенный график

. Для этого к оси φ графика

проводим в любом свободном месте поля чертежа прямую под углом 45°. Далее из точек 1’,2', 3', . . . ,18' проводим прямые, параллельные оси φ. A из точек 1", 2", 3",. ,18" — прямые, также вначале параллельные оси φ, а затем перпендикулярные ей. Полученные таким образом точки пересечения 1", 2", 3" 16" соединяем лавной кривой.

3) Проводим касательные к полученной кривой под углом

, которые после пересечения ограничивают область (она на чертеже заштрихована), любая точка которой может быть выбрана за центр вращения кулачка. Выбираем за центр вращения кулачка точку О.

4) Соединяем точку О с началом координат совмещенного графика. Отрезок изображает минимальный радиус кулачка R_min в масштабе

.
4.2. Построение профиля кулачка
Из произвольной точки О проводим окружность радиуса R_min. От точки 0 вверх откладываем перемещения толкателя, взятые с графика

. Получим точки 1, 2, 3. .... 15, 18. Наиболее удаленную точку 9 соединяем прямой с точкой О и этим радиусом проводим окружность. От прямой О - 9 откладываем фазовые углы ф_у =50°,

° и

= 50°. Углы нужно откладывать против вращения кулачка. Дуги окружности. соответствующие фазовым углам ф_у и

делим на 9 равных частей, получаем соответственно точки 1*, 2*, .... 8,*, 9*. 10*, . . . ,18*. Эти точки соединяем с центром О. Затем из точки О (центра вращения кулачка) проводим дуги радиусами О1, О2, О3 и т. д. до пересечения с соответствующими отрезками. Получим точки 1₀, 2₀, 3_о, ..., 18_о. Соединив эти точки плавной кривой, получим теоретический профиль кулачка.

Список литературы

Артоболевский И.И. Теория механизмов и машин М., Наука. 1975.
Турбин Б.И., Карлин В.Д. Теория механизмов и машин. М.. Машиностроение. 1980.

Артоболевский И.И., Эдельштейн Б.В. Сборник задач по теории механизмов и машин. М., Наука. 1975.

4. Баранов Г.Г. Курс теории механизмов и машин М. Машиностроение, 19X0.

1 2 3