Кинематический анализ механизма

Название	Кинематический анализ механизма
Дата	09.11.2018
Размер	1.87 Mb.
Формат файла
Имя файла	kontr_tmm.doc
Тип	Исследование #55953
страница	1 из 3

1 2 3

Оглавление 2

Задание 3

Введение 4

1. Кинематический анализ механизма 5

1.1. Проектирование кривошипно-ползунного механизма 5

1.2. Структурное исследование механизма 5

1.3. Построение схемы механизма 5

1.4. Построение планов скоростей механизма 6

1.5. Построение планов ускорений механизма 12

1.6. Кинематические диаграммы точки D ползуна 3 18

1.7. Расчет скоростей и ускорений ползуна методом Зиновьева. 21

Метод Зиновьева. Положение 1. 22

Метод Зиновьева. Положение 4. 25

Метод Зиновьева. Положение 5. 26

Метод Зиновьева. Положение 6. 27

2. Силовой расчет рычажного механизма 28

2.1. Определение движущей силы Р (силы сопротивления, приложенной к ползуну 5) 28

2.2. Определение сил инерции звеньев 28

2.3. Определение реакций в кинематических парах групп Ассура 29

2.4. Силовой расчет ведущего звена механизма 36

2.5. Рычаг Н.Е. Жуковского. 40

3. Расчет маховика. 42

4. Синтез кулачкового механизма. 52

4.1. Определение минимального радиуса кулачка Rmin 52

4.2. Построение профиля кулачка 52

Список литературы 54

Задание

по схеме №1 вариант 5.

Введение

Объектом исследования является кривошипно-ползунный механизм.

В курсовом проекте исследованию подлежат рычажный и кулачковый механизм.

Рычажный механизм служит для преобразования возвратно-поступательного перемещение ползуна 3 из вращательного движения кривошипа 1.

В рычажных механизмах угловая скорость непостоянна и для более равномерного движения на валу кривошипа установлен маховик.

Для управления зажимом деталей применяется кулачковый механизм, который служит для преобразования вращательного движения в поступательное движение ведомого звена.

1. Кинематический анализ механизма

1.1. Проектирование кривошипно-ползунного механизма
Значения длин кривошипа АВ и шатуна ВС даны по условию.

м,

м.

м,

м.
1.2. Структурное исследование механизма
Определяем степень подвижности механизма по формуле

П.Л. Чебышева.

где

— число подвижных звеньев (кривошип АВ, шатун ВС, ползун D);

— число кинематических пар пятого класса (A(0;1), B(1,2), C(2,3), D(3,0));

— число кинематических пар четвертого класса..

Определяем класс и порядок механизма. Для этого разделим механизм на группы Ассура. Этот механизм состоит из одной группы Ассура II класса 1-го порядка 2-го вида (рис. 1, а), одной группы Ассура II класса 2-го порядка 2-го (рис. 1, а) вида и механизма I класса, состоящего из ведущего звена 1 и стойки 6.

В целом рассматриваемый механизм II класса 2-го порядка.
1.3. Построение схемы механизма
Масштаб схемы. Приняв на чертеже (см. лист 1 приложения) отрезок АB = 25 мм, находим:

.

В принятом масштабе вычерчиваем схему механизма. Для построения 6 положений звеньев механизма разделим траекторию, описываемую точкой B кривошипа, на 6 равных частей. В качестве нулевого принимаем то положение кривошипа, при котором точка C ползуна занимает крайнее левое положение. Из отмеченных на окружности точек В₀, В₁…В₆ раствором циркуля равным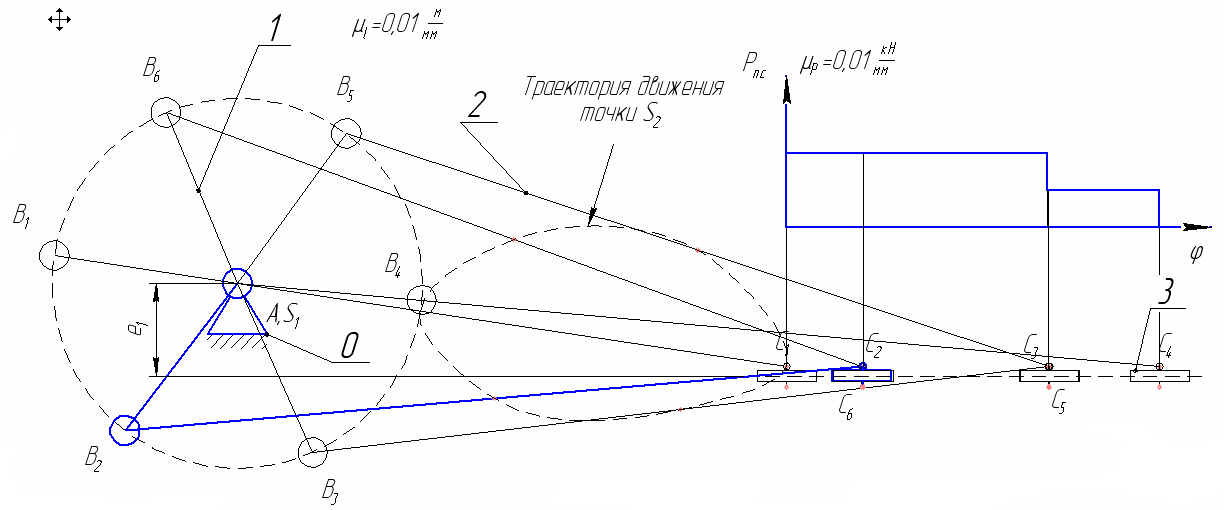

мм, намечаем на линии движения точки С точки 0, 1, 2 и т. д. (положения точки С). Соединяем точку В₁ с точкой 1, точку В₂ с точкой 2 и т. д. Получаем положения точки С.

1.4. Построение планов скоростей механизма
Определяем скорость точки В.

.

Построение начинаем от ведущего звена. Из точки р, принятой за полюс плана скоростей (лист 1 приложения), откладываем в направлении вращения кривошипа АВ вектор скорости точки В : рb = 52,4 мм.

Построение плана скоростей группы Ассура II класса 1-го вида (звенья 2 и 3) производим по уравнению: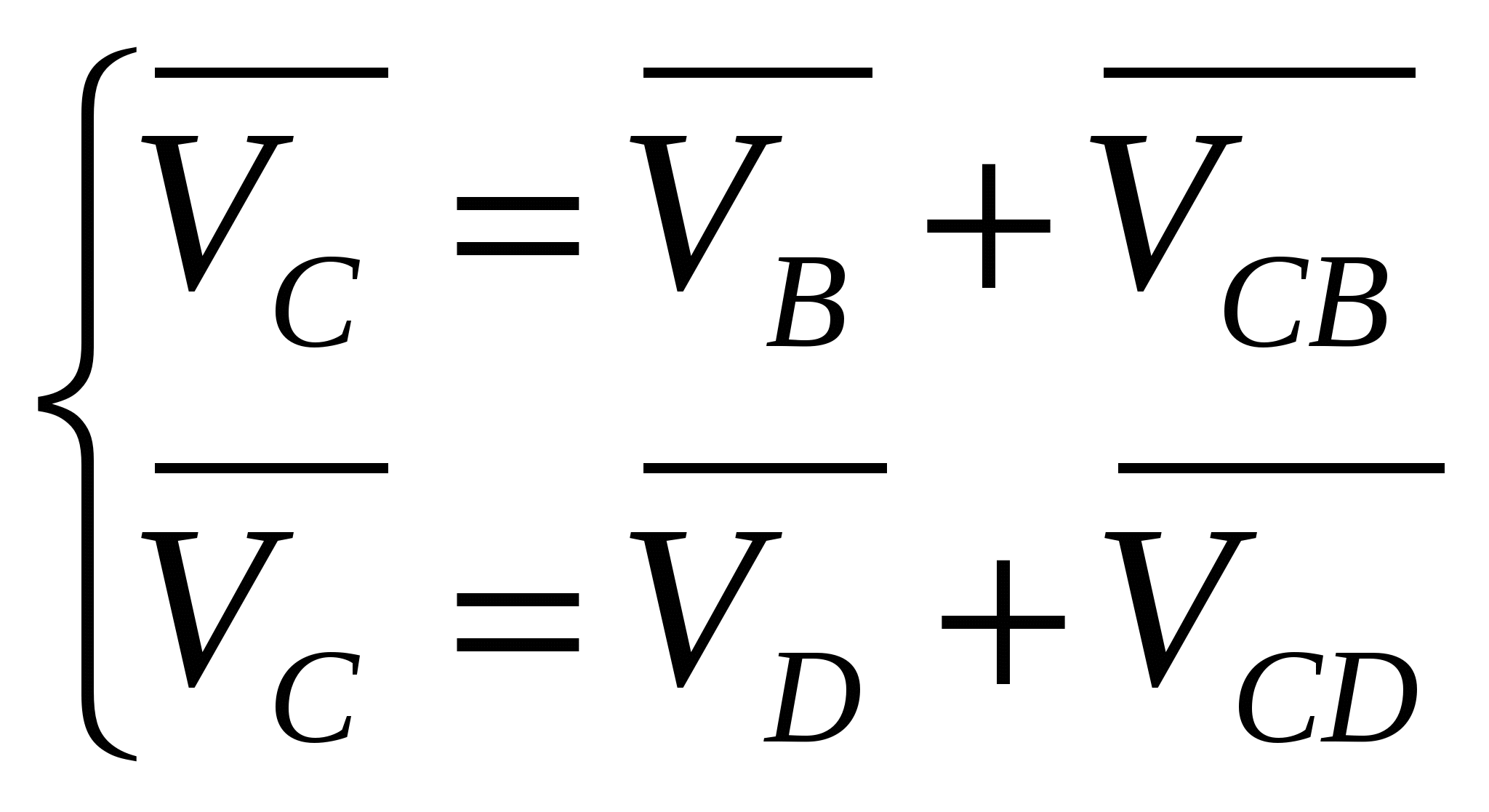

— вектор скорости точки C во вращательном движении относительно точки B, направлена перпендикулярно оси звена ВC;

— вектор скорости точки C во вращательном движении относительно точки D, направлена параллельно оси движения ползуна C;

.

Из точки b проводим линию, перпендикулярную оси звена ВC, а из полюса р плана скоростей — линию, параллельную оси движения ползуна С. Точка с пересечения этих линий даст конец вектора искомой скорости

. Масштаб планов скоростей вычисляем по формуле

Скорости точек S₂ и S₃определяем по правилу подобия. Истинное значение скорости каждой точки определяем по формулам:

.

Расчет скоростей производим для всех положений.

Положение №1.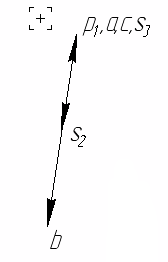

.

Положение №2.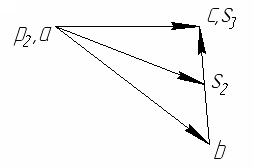

.

Положение №3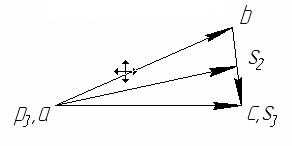

.

Положение №4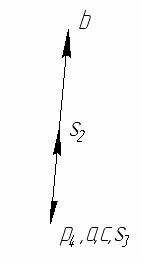

.

Положение №5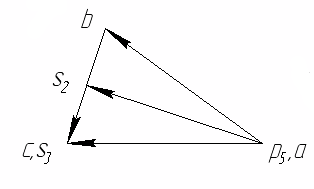

.

Положение №6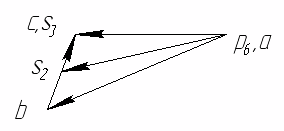

.
Получение значения сводим в табл. 1.

Таблица 1

Значения скоростей точек механизма

Длины векторов скоростей на плане скоростей
Длина вектора, мм	№ положения
Длина вектора, мм	1	2	3	4	5	6
pb	52,4	52,4	52,4	52,4	52,4	52,4
bc	52,4	31,9	21,4	52,4	32,5	21,5
pc	0	38,9	50,4	0	52,6	41
pd	0	38,9	50,4	0	52,6	41
pg	0	38,9	50,4	0	52,6	41
pS2	26,2	43,3	50,3	26,2	49,9	45,8
pS3	0	38,9	50,4	0	52,6	41

Обозначение скорости точки, м/с	№ положения
Обозначение скорости точки, м/с	1	2	3	4	5	6
b	26,2	26,2	26,2	26,2	26,2	26,2
bc	26,2	15,95	10,7	26,2	16,25	10,75
c	0	19,45	25,2	0	26,3	20,5
d	0	19,45	25,2	0	26,3	20,5
g	0	19,45	25,2	0	26,3	20,5
S2	13,1	21,65	25,15	13,1	24,95	22,9
S3	0	19,45	25,2	0	26,3	20,5

масштабный коэффициент			0,5

Определяем (табл. 2) угловую скорость шатуна ВС для всех положений по формуле:

,

Положение №1

Положение №2

Положение №3

Положение №4

Положение №5

Положение №6

Таблица 2

	Значения угловых скоростей
Обозначение угловой скорости	№ положения
Обозначение угловой скорости	1	2	3	4	5	6
ω2	13,1	7,975	5,35	13,1	8,125	5,375

Длина звена BC	2	м

Направление угловой скорости звена ВС определяется следующим образом. Переносим мысленно вектор bс с плана скоростей в точку С шатуна 2 и наблюдаем направление поворота этого звена вокруг точки В. Например, в положении 2 угловая скорость ω₂ направлена против часовой стрелки.
1.5. Построение планов ускорений механизма
Построение плана ускорений рассмотрим для всех положений механизма (лист 2 приложения). Так как кривошип АВ вращается с постоянной угловой скоростью, то точка В кривошипа будет иметь только нормальное ускорение, величина которого равна

м/с².

Масштаб плана ускорений определяется по формуле

.

где πb = 68,4 мм — длина отрезка, изображающего на плане ускорений вектор нормального ускорения точки В кривошипа АВ.

Из произвольной точки π — полюса плана ускорений проводим вектор πb параллельно звену АB в направлении от точки B к точке A.

Построение плана ускорений группы Ассура II класса 1-го вида (звенья 2 и 3) производим согласно векторному уравнению: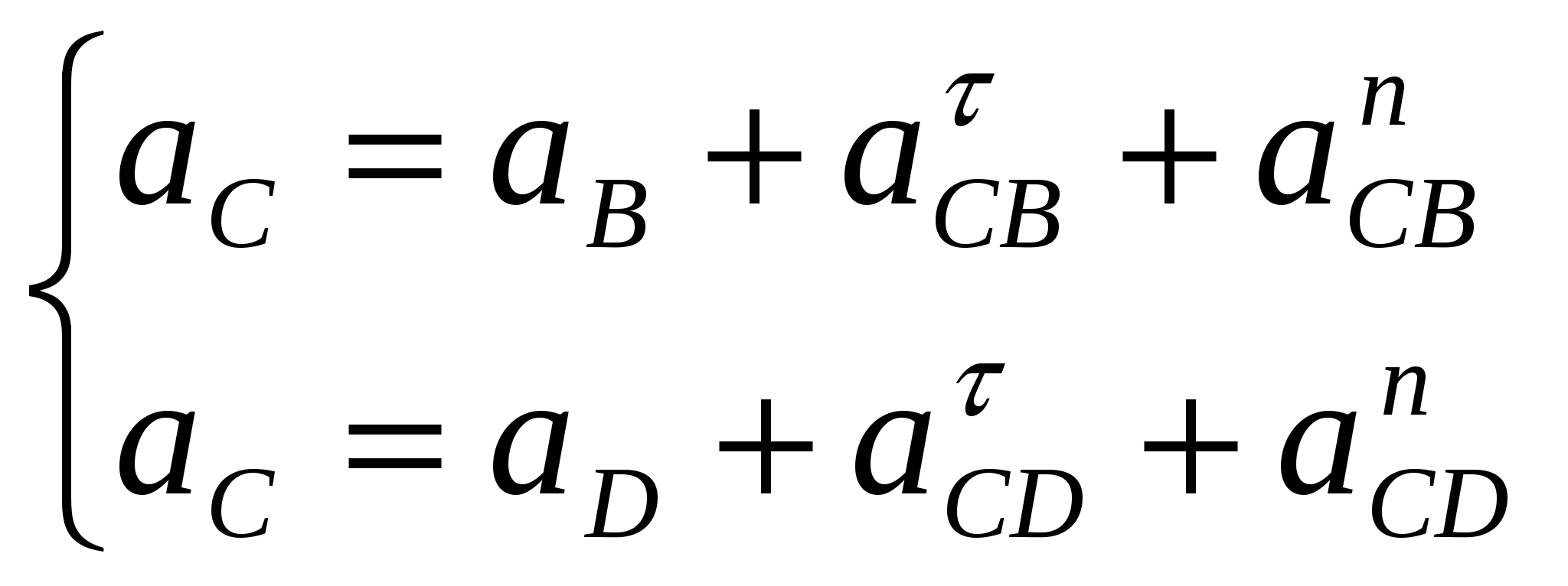

где

— ускорение точки В;

— нормальное ускорение точки C шатуна BC при вращении его вокруг точки B, направлено вдоль оси звена ВC от точки C к точке B,

— тангециальное ускорение точки C при вращении его вокруг точки B, направлено перпендикулярно оси звена ВС.

м/с².

Его масштабная величина равна 17,16 мм на плане ускорений.

— касательное ускорение точки С при вращении его вокруг точки D, направлено перпендикулярно к оси звена CD.

На плане ускорений через точку π проводим прямую, параллельную оси звена AB, и откладываем на ней в направлении от точки B к точке A отрезок πb = 68,4 мм. Через конец этого вектора проводим прямую, параллельную, а потом перпендикулярную к оси звена ВC. Затем через полюс π проводим прямую, параллельную, а потом перпендикулярную оси CD. Точка пересечения этих прямых определит конец вектора πc. Точку S₂ на плане ускорений находим по правилу подобия, пользуясь соотношением отрезков.

.

Для положения №1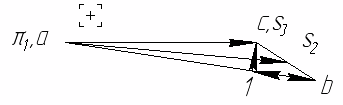

Для положения №2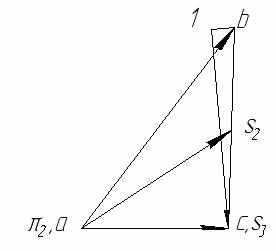

Для положения №3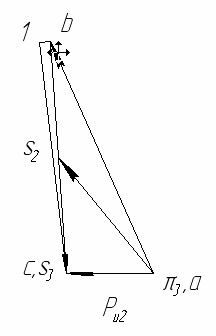

Для положения №4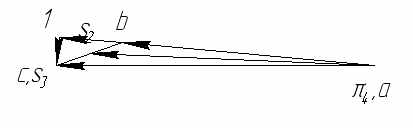

Для положения №5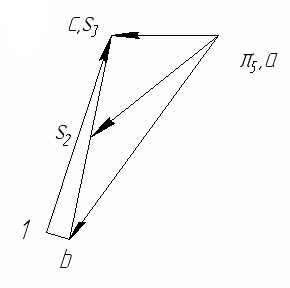

Для положения №6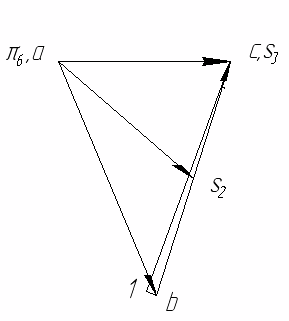

Численное значение ускорений точек звеньев сведем в таблицу 3.
Таблица 3.

Ускорения точек звеньев механизма

Длины векторов скоростей на плане скоростей

Длина вектора

мм

№ положения

68,4

bcⁿ

17,161

6,360063

2,86225

17,161

6,601563

2,889063

bc^t

7,77

50,4

62,59

7,77

56,09

66,14

51,83

39,8

23,38

85,91

28,84

46,34

51,83

39,8

23,38

85,91

28,84

46,34

51,83

39,8

23,38

85,91

28,84

46,34

pS2

60,29

48,55

40,36

76,8

44,25

48,14

pS3

51,83

39,8

23,38

85,91

28,84

46,34

Обозначение

скорости

точки, м/с

№ положения

1368

bcⁿ

343,22

127,2013

57,245

343,22

132,0313

57,78125

bc^t

155,4

1008

1251,8

155,4

1121,8

1322,8

1036,6

796

467,6

1718,2

576,8

926,8

1036,6

796

467,6

1718,2

576,8

926,8

1036,6

796

467,6

1718,2

576,8

926,8

1205,8

971

807,2

1536

885

962,8

1036,6

796

467,6

1718,2

576,8

926,8

масштабный коэффициент

Определяем угловые ускорения ε₂звена 2,

рад/с²,

Положение №1

рад/с².

Положение №2

рад/с².

Положение №3

рад/с².
Положение №4

рад/с².

Положение №5

рад/с².

Положение №6

рад/с².
Для определения направления углового ускорения ε₂ мысленно переносим вектор 1с с плана ускорений в точку С звена ВС. Считая точку В неподвижной, замечаем, что поворот звена будет против часовой стрелки.

Численное значение угловых ускорений сведем в таблицу 4.
Таблица 4

	Значения угловых ускорений
Обозначение углового ускорения	№ положений
Обозначение углового ускорения	1	2	3	4	5	6
ε₂	77,7	504	625,9	77,7	560,9	661,4

Длина звена BC	2	м

1.6. Кинематические диаграммы точки D ползуна 3
График отстояний. Для построения графика отстоянии точки D ползуна откладываем на оси абсцисс отрезок х = 180 мм, изображающий период Т одного оборота кривошипа, и делим его на 6 равных частей. От точек 0, 1, 2,..., 6 откладываем ординаты 1 — 1*, 2—2*, ..., 6 — 6*. соответственно равные расстояниям 0—1, 0—2, ..., 0—6, проходимые точкой D от начала отсчета.

Вычисление масштабов графика отстояний.

Так как ординаты графика отстояний равны расстояниям, измеренных на планах механизма, то масштаб графика будет равен масштабу схемы механизма, т.с.

м/мм.

График скоростей. Строится графическим дифференцированием графика отстояний по методу хорд. Он заключается в следующем:

Криволинейные участки графика отстояний заменяем хордами 0*—1*, 1*—2* … 6*—6*. Намечаем прямоугольные оси v и t. Ось t продолжаем влево от оси ординат. Выбираем произвольной длины полюсное расстояние Н. В нашем случае 20 мм. Из полюса р проводим наклонные прямые р—1’, р—2' … р—6', параллельные хордам 0*—1*, 1*—2*, 6*6*. Из середины интервалов 0—1, 1—2 6 — 6 проводим перпендикуляры к оси абсцисс (штриховые линии). Из точек 1’, 2', .... 6' проводим параллельные оси абсцисс до пересечения с соответствующими перпендикулярами. Получаем точки 1", 2", .... 6 . Соединяем их плавной кривой.

Масштаб графика скоростей:

.

График ускорений. Строится аналогично графику •скоростей. Масштаб его по оси ординат равен: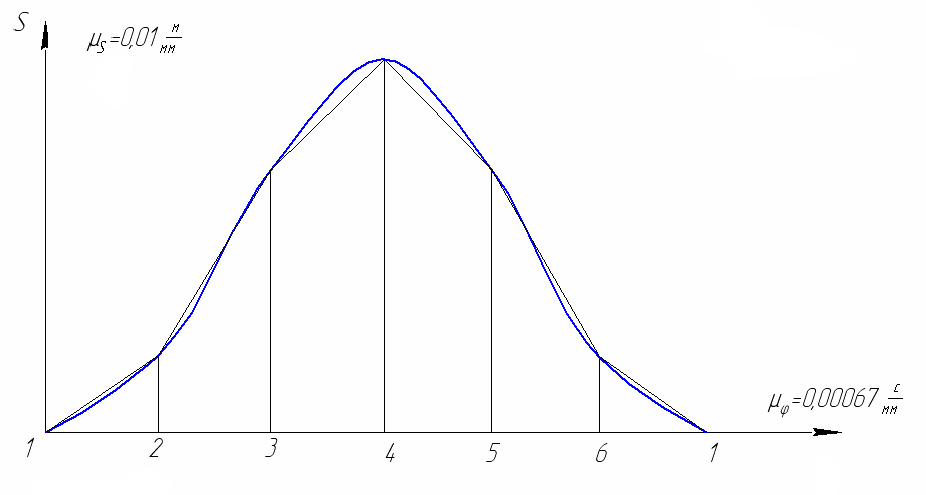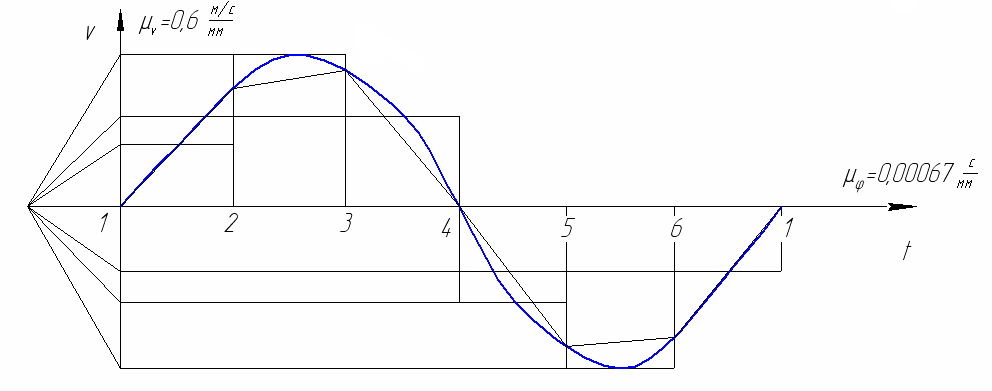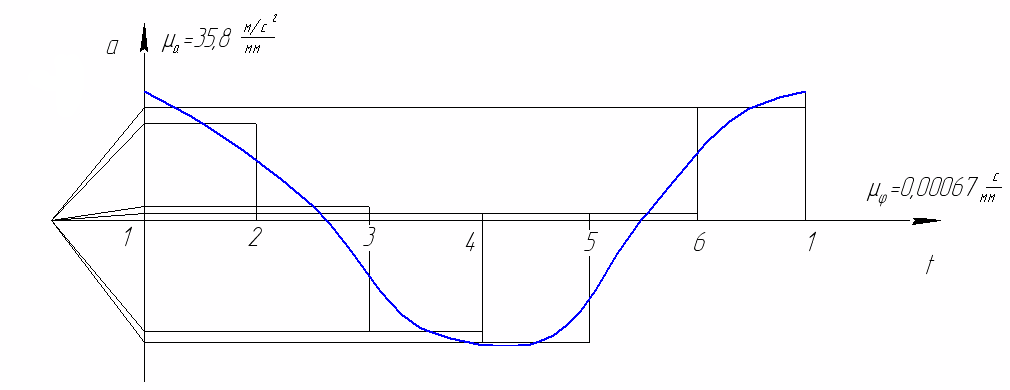

1.7. Расчет скоростей и ускорений ползуна методом Зиновьева.
Это аналитический метод.

Зависимости для расчета следующие.

1.

,

2.

,

3.

,

4.

,

5.

,

6.

,

Рассчитываем по вышеприведенным формулам для каждого положения механизма и сводим полученные данные в таблицу и сравниваем два метода.

Метод Зиновьева. Положение 1.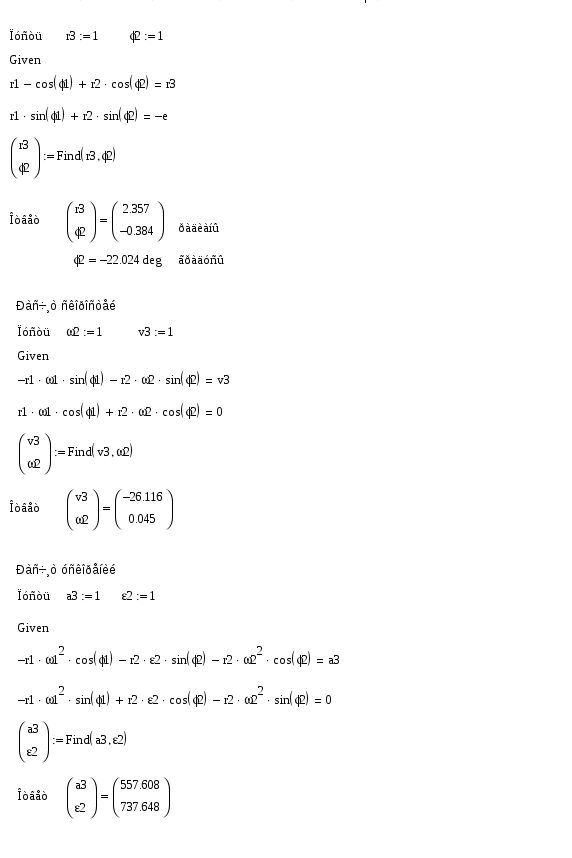

Метод Зиновьева. Положение 2.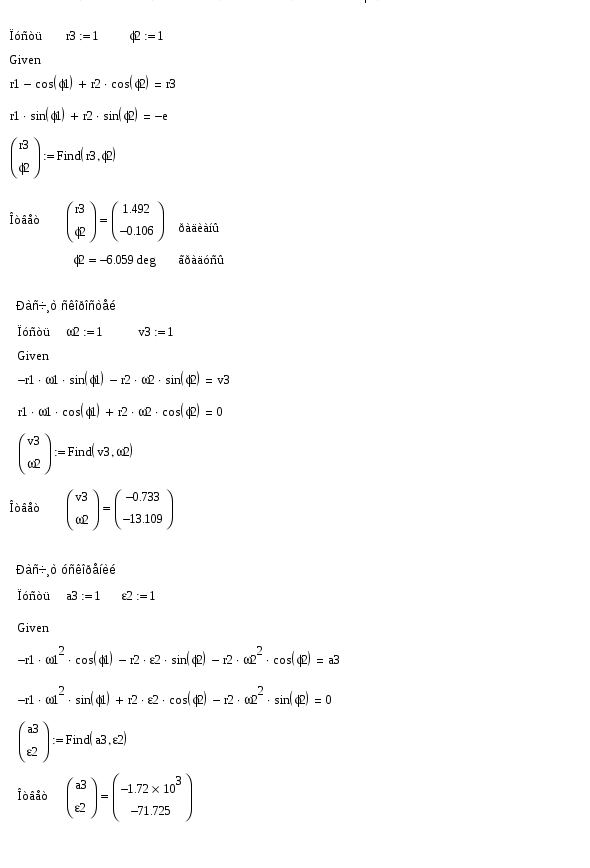

Метод Зиновьева. Положение 3.

Метод Зиновьева. Положение 4.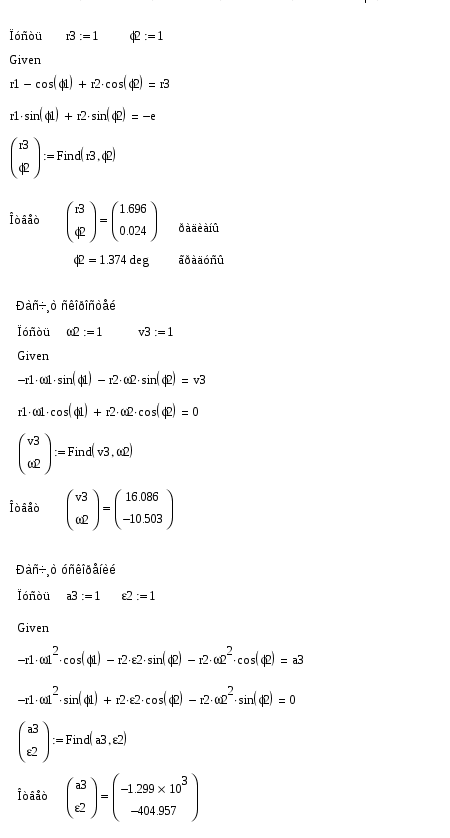

Метод Зиновьева. Положение 5.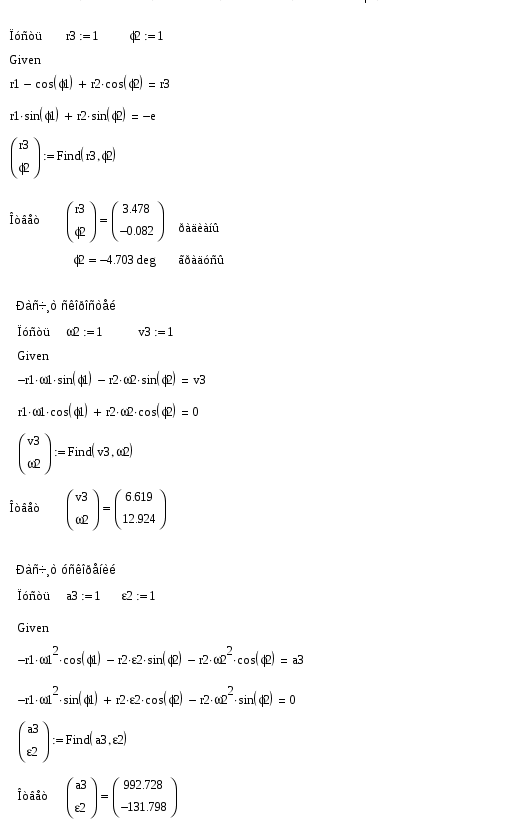

Метод Зиновьева. Положение 6.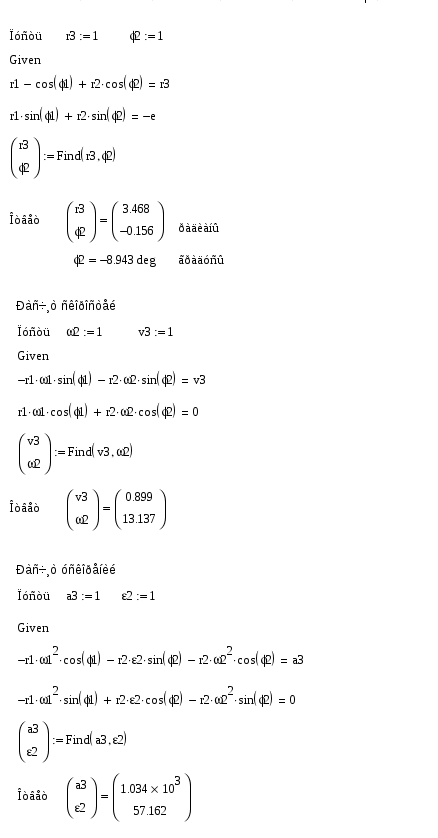

1 2 3