ФокинА_2РГР. Кинематика движения точки и твердого тела
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
Расчетно-графическое задание по кинематике РГР-2 КИНЕМАТИКА ДВИЖЕНИЯ ТОЧКИ И ТВЕРДОГО ТЕЛА Группа Студент Фокин А.А. Оценка работы Дата Преподаватель Задача 1 По данным уравнениям движения точки М установить вид её траектории и для момента времени t1 найти положение точки на траектории (х1 (м), y1 (м)); её скорость V (м/c) , полное, касательное и нормальное ускорения ( a (м/c2); aτ (м/c2); an (м/c2) ), а так же радиус кривизны траектории в данной точке (p(м)). Вариант задания: Ф – 22, А – 1. В - 23 Задание по варианту x = 3-3*t2 (м); y = 4-5*t2 (м); t1 = 0,5 (c) Найти: х1 (м), y1 (м); V (м/c); a (м/c2); aτ (м/c2); an (м/c2); p(м); Решение Получим уравнение траектории: Установим вид уравнения, связывающего функции хи у, по которому судят о траектории движения точки. Умножим все части уравнения x = 3-3*t2 на 1,66: 1,66х = 5-5*t2 Выразим из одного уравнения -5t2и подставим в другое. -5*t2 = 1,66х-5 у = 4-(1,66х-5) = 4-1,66х+5 = 9-1,66х Уравнение траектории: y = 9-1,66х Полученное уравнение траектории – это уравнение прямой, проходящей через точки с координатами (0; 9) и (5,4; 0). Подставим значение t0, t0 = 0 с, в параметрические уравнения х и у: x0= 3-3*02 = 3 y0= 4-5*02 = 4 Т.е. точка начала движения – (3; 4) Подставим значение t1 в параметрические уравнения х и у: x1= 3-3*0,52 = 2,25 y1= 4-5*0,52 = 2,75 Т.е. через 0,5 секунд точка имела координаты (2,25; 2,75) Таким образом, точка движется по прямой сверху вниз (по направлению стрелки на рисунке). 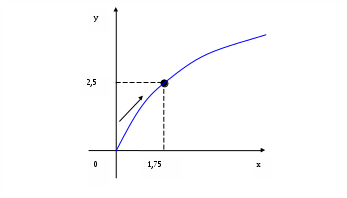 Скорость V2=Vx2+Vy2 , где V – полная скорость, а Vx и Vy проекции вектора полной скорости на оси Ох и Оy соответственно; Vx=d(3-3*t2)/dt Vy=d(4-5*t2)/dt Vx = -6t = -3 м/с, при t1 = 0,5 Vy = -10t = -5 м/с V2 = (5)2 + (3)2 = 25+9 = 34 V = 5.8 м/с Полное ускорение ax=d2x/dt2; ay=d2y/dy2 a2= ax2+ay2, где а – полное ускорение, а аx и аy проекции вектора полного ускорения на оси Ох и Оy соответственно; ax = d(-6*t)/dt = -6 ay = d(-10t)/dt = -10 a2= ax2+ay2 a= √62+102 = 11.7 м/c2 Касательное ускорение aτ = dV/dt; V = √(36t2+100t2) aτ = d(√(36t2+100t2))/dt = 11.7 м/c2, при t1 = 0,5 Нормальное ускорение an2= a2 – aτ2 an 2 = 11.72 – 11,72 = 0 an = 0 м/c2 Радиус кривизны траектории p = V2/an p =(5.8)2 /0 = нет корней Ответ: Координаты точки в момент времени t1 на траектории у = 9-1,66х, t1(2,25; 2,75) Скорость точки равна V=5,8 м/с Ускорение точки (полное) a=11,7 м/с2 Ускорение касательное aτ= 11,7 м/с2 Ускорение нормальное an= 0 м/с2 Задача 2 № схемы механизма – 22 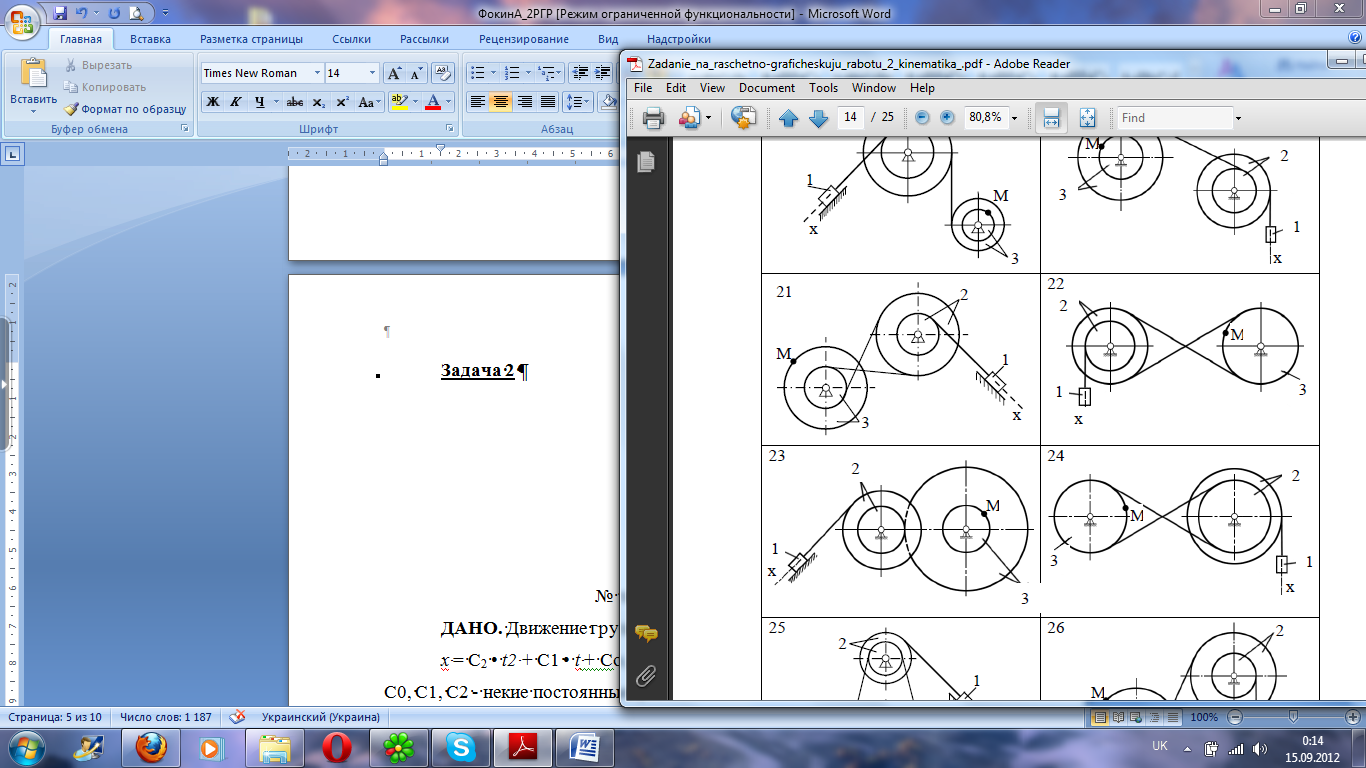 № таблицы исходных данных – 1 ДАНО. Движение груза 1 описывается выражением: х = С2 • t2 + С1 • t + Со, где t - время в секундах; С0, С1, С2 - некие постоянные. В начальный момент времени t0 = 0, начальная координата груза равна х=х0, а начальная скорость х0= V0. В момент времени t = t2 координата груза 1 равна х = х2 . Размеры шкивов 2 и 3 характеризуются радиусами R2, r2, R3, r3. ОПРЕДЕЛИТЬ: уравнение движения груза 1 (x(t)); скорость и ускорение груза 1. в момент времени t = t1 ( V1, a1 ); угловые скорости и угловые ускорения шкива 2 (ω2 , ξ2 ) и шкива 3 (ω3 , ξ3 )в момент времени t = t1 ; скорость, ускорение точки М (VM, aM) одного из шкивов механизма при t = t1. ПРИМЕЧАНИЕ: при отсутствии проскальзывания одного тела по поверхности другого соприкасающиеся точки этих тел имеют одинаковые скорости и касательные ускорения.
Решение Заданный механизм представлен на рис.1(схема 15), уравнение движения груза 1 описывается выражением: х = C2t2 + C1t + С2 . В начальный момент времени t0 начальная координата груза х0, начальная скорость V0 . Итак: груз 1 движется поступательно вниз; шкив 2 вращается вокруг неподвижной оси O2z2 (рис.2); шкив 3 вращается вокруг неподвижной оси O3z3 (рис.2). Уравнение движения груза 1 х = C2t2 + C1t + С2 (1) Скорость груза 1 определим, продифференцировав закон движения по времени: V = x’ = 2 . C2t + C1 (2) Касательное ускорение груза 1 определим, получив вторую производную от уравнения (2): a τ= V’= x’’ = 2.C2 = const (3) Таким образом, ускорение не зависит от времени t. Следовательно, ускорение есть величина постоянная, а движение груза - равноускоренное. При движении по прямой нормальное ускорение отсутствует (an=0), поэтому полное ускорение груза определяется только касательной составляющей (a=aτ). Уравнение траектории движения груза x=C2t2+C1t+C0 (1); V=x`=2C2t+C1 (2); a=V`=2C2=const (3); t0=0, x0=0.07; подставляем в (1): 0.07 = C2*0 + C1*0 + C0; C0=0.07; подставляем t0=0 в (2): V0=2C2t0+C1; V0=2C2*0+C1; C1=V0=0.06; t2=2, x2=1,03; подставляем в (1): 1,03 = C2*22+0.06*2+0.07; C2=0.21; Таким образом x=0.21t2+0.06t+0.07 2) Скорость груза в момент времени t1: V1=2С2t1+C1; V1=2*0.11*2+0.02=0,46; V1=0,46 м/с; Ускорение груза в момент времени t1: a1=2C2=0.42 м/с2 3) Т.к. ремень нерастяжим, то VЕ=V1, aτE=a1. Угловая скорость шкива находится по формуле: ω=V/R, где R – радиус шкива. (4) Для шкива 2: ω2 = VЕ/r2; ω2 = 0,46/0.57 = 0,88 рад/с; Угловое ускорение находится по формуле ξ = aτE/r (5); ξ2 = aτE/r2; ξ2 = 0.42/0.57 = 0.74 рад/с. Направление углового ускорения ε2 соответствует направлению вектора касательного ускорения aEτ (против хода часовой стрелки) (рис.2); Модуль скорости точки К VК = ω2КО2 где КО2 - кратчайшее расстояние от точки до оси вращения O2 z2. VK = ω2R2 = 0,88*0,81 = 0,71 м/с Направлен вектор скорости VК перпендикулярно к кратчайшему расстоянию КО2 и соответствует направлению угловой скорости ω2 (рис.2). Касательное ускорение точки К aКτ = ε2КО2 = ε2R2 aКτ = 0.74*0,81 = 0.6 м/с2 Направлен вектор касательного ускорения точки К перпендикулярно кратчайшему расстоянию от точки К до оси вращения, т. е. aКτ _|_КО2 и соответствует направлению углового ускорения ε2. Так как ремень нерастяжимый, то VМ = VK = 0,71 м/с aМτ= aКτ = 0.6 м/с2 Направления векторов VN и aNτпоказаны на рис.2. Из кинематики вращения тела 3 вокруг неподвижной оси вращения O3 z3: угловая скорость ω3 = VМ/МO3 где МO3 - кратчайшее расстояние от точки М до оси вращения O3 z3 . ω3 = VМ/R3 = 0,71/0.6 = 1,2 Направлена угловая скорость по часовой стрелке и соответствует направлению вектора скорости VМ (рис. 2)  E   K O2 O3 Рис. 2. Угловое ускорение ε3 = аМτ/МO3 = 0.6/0.6 = 1 Направление углового ускорения ε3 соответствует направлению вектора касательного ускорения aNτ(по часовой стрелке) (рис.2). Нормальное ускорение точки М: aМn = ω32MO3 aМn = ω32*R3 = 1,22*0.6 = 0.86 м/с2 Направлен вектор нормального ускорения по радиусу MО3 в сторону оси вращения (рис.2). Полное ускорение точки М есть векторная сумма двух ускорений aМ = aМn + aМτ Его величина: aМ = (aМn)2 + (aМτ)2; aМ = 0.74+ 0.36= 1,1 м/с2 Направление вектора aМ показано на расчетной схеме (рис.2) диагональю прямоугольника, построенного на векторах нормального и касательного ускорения как на сторонах. Так как вектор ускорения a1 и вектор скорости V1 груза 1 направлены в одну сторону и при этом ускорение есть величина постоянная, то груз 1, тела 2 и 3, а вместе с ними и точка М совершают равноускоренное движение. ОТВЕТ. V M = 0,71 м/с, aМ = 1,1 м/с2
| |||||||||||||||||||||||||||||||||||||||||||||
