Реферат Кинематика. Махметова А.Ш. Задание 1. Кинематика и динамика материальной точ. Кинематика и динамика материальной точки. Динамика твердого тела
 Скачать 0.59 Mb.
|
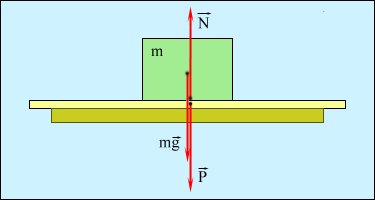 По определению, сила  и называется весом тела. Из приведенных выше соотношений видно, что  т. е. вес тела равен силе тяжести  , но эти силы приложены к разным телам! Рисунок 8 Вес тела и сила тяжести.  - сила тяжести,  - сила реакции опоры, - сила давления тела на опору (вес тела).  Если тело неподвижно висит на пружине, то роль силы реакции опоры (подвеса) играет упругая сила пружины. По растяжению пружины можно определить вес тела и равную ему силу притяжения тела Землей. Рассмотрим теперь случай, когда тело лежит на опоре (или подвешено на пружине) в кабине лифта, движущейся с некоторым ускорением  относительно Земли. Система отсчета, связанная с лифтом, не является инерциальной. На тело по-прежнему действуют сила тяжести и сила реакции опоры  но теперь эти силы не уравновешивают друг друга. По второму закону Ньютона  Сила  действующая на опору со стороны тела, которую и называют весом тела, по третьему закону Ньютона равна  Следовательно, вес тела в ускоренно движущемся лифте есть  Пусть вектор ускорения направлен по вертикали (вниз или вверх). Если координатную ось OY направить вертикально вниз, то векторное уравнение для можно переписать в скалярной форме: = m(g - a). В этой формуле величины P, g и a следует рассматривать как проекции векторов 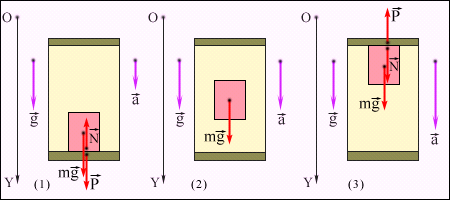,  и на ось OY. Так как эта ось направлена вертикально вниз, g = const > 0, а величины P и a могут быть как положительными, так и отрицательными. Пусть, для определенности, вектор ускорения направлен вертикально вниз, тогда a > 0 (рис. 9). Рисунок 9 Вес тела в ускоренно движущемся лифте. Вектор ускорения направлен вертикально вниз. 1) a < g, P < mg; 2) a = g, P = 0 (невесомость); 3) a > g, P < 0. Из формулы (*) видно, что если a < g, то вес тела P в ускоренно движущемся лифте меньше силы тяжести. Если a > g, то вес тела изменяет знак. Это означает, что тело прижимается не к полу, а к потолку кабины лифта («отрицательный» вес). Наконец, если a = g, то P = 0. Тело свободно падает на Землю вместе с кабиной. Такое состояние называется невесомостью. Оно возникает, например, в кабине космического корабля при его движении по орбите при выключенных реактивных двигателях. Если вектор ускорения направлен вертикально вверх, то a < 0 и, следовательно, вес тела всегда будет превышать по модулю силу тяжести. Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают космонавты, как при взлете космической ракеты, так и на участке торможения при входе корабля в плотные слои атмосферы. Проявление сил инерции и силы Кориолиса на Земле Среди сил инерции выделяют следующие: · простую силу инерции · центробежную силу, объясняющую стремление тел улететь от центра во вращающихся системах отсчёта; · силу Кориолиса, объясняющую стремление тел сойти с радиуса при радиальном движении во вращающихся системах отсчёта. Все инерциальные системы отсчета имеют право двигаться с постоянной скоростью относительно друг друга. Система отсчета, которая движется с переменной скоростью, будет уже неинерциальной. По отношению к такой системе отсчета законы механики перестают действовать. Действительно, если система движется с переменной скоростью  относительно инерциальной системы К, то правило сложения скоростей будет выглядеть: Тогда для ускорения одержим:   Где:  - ускорение материальной точки в системе К, - ускорение материальной точки в системе К - ускорение системы , относительно системы КУмножим все члены формулы на массу материальной точки m:  Или  И сразу видим, что сила, которая действует на материальную точку в системе , не равна силе, действующей на эту же материальную точку в системе К, как это было, когда обе системы были инерциальными. Они отличаются на величину -, которая называется силой инерции:  Таким образом, в неинерциальной системе отсчета появилась дополнительная сила - сила инерции, и именно в этом значении следует понимать заявление о том, что в неинерциальных системах отсчета законы механики не действуют. Особенности сил инерции 1. В отличие от других сил, силы инерции не являются силами взаимодействия. Нельзя указать тело, которое является источником сил инерции. Поэтому силы инерции иногда называют «фиктивными силами», или «псевдосилами». 2. Но силы инерции вполне реальны, их можно измерить. По появлению сил инерции можно судить об ускорении системы отсчета. . Силы инерции пропорциональны массе, как и силы тяготения. Если наперед неизвестно, движется ли система отсчета с ускорением, или тело находится в гравитационном поле, то отличить силы инерции и гравитации невозможно. Это утверждение составляет содержание знаменитого принципа Эквивалентности: Движение тела по отношению к неинерциальной системе отсчета эквивалентно его движению относительно инерциальной системы, под воздействием всех тел, которые реально взаимодействуют с ним, а также дополнительного поля тяготения. Силы инерции во вращающейся системе отсчета 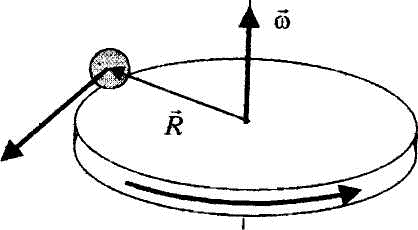 Выбреем как неинерциальную систему отсчета диск радиуса R, которая вращается вокруг собственной оси с постоянной угловой скоростью  (рис 10). Система неинерциальная, несмотря на равномерность вращения, поскольку каждая точка диска имеет нормальное ускорение, которое не равно нулю. Пускай материальная точка массой m по отношению к диску движется с постоянной скоростью  . Наблюдатель в этой системе зафиксирует нормальное ускорение материальной точки: Наблюдатель, который находится в неподвижной инерциальной системе отсчета, тоже констатирует, что материальная точка движется равномерно по кругу, но с другой линейной скоростью:  И с другим нормальным ускорением:  Выразим из этой формулы нормальное ускорение в неинерциальной системе отсчета:  Умножив уравнение на массу, получим силы:  Из полученного уравнения видно, что сила в неинерциальной системе отсчета равна силе в инерциальной системе отсчета плюс еще две силы инерции  - центробежная сила инерции и сила инерции Кориолиса.Центробежная сила инерции В общем случае при произвольном относительном размещении векторов угловой скорости и радиус-вектора материальной точки формула для центробежной силы инерции будет иметь такой вид:  Несмотря на сложные векторные произведения, центробежная сила всегда перпендикулярна оси вращения и направлена по радиусу от центра круга. Особенности центробежной силы: 1. действует как на неподвижное тело, так и на движущееся; 2. пропорциональна массе тела; . зависит от угловой скорости неинерциальной системы; . возрастает с отдалением от оси вращения Земля вращается относительно своей оси, поэтому она неинерциальная система. Центробежная сила также проявляется в изменении силы веса Р в зависимости от широты местности (Рис.11). Вес тела - векторная сумма силы тяготения, направленной к центру Земли и центробежной силы инерции, направленной перпендикулярно оси вращения:  По теореме синусов:  И  Угол  небольшой, поскольку центробежная сила мала по сравнению с весом. На полюсе центробежная сила равна нулю, а на экваторе она максимальна:  Таким образом, из-за центробежной силы вес тела на полюсе больше веса на экваторе на 0,35%. Разница невелика для обычного обитателя Земли. Но она имеет большое значение во время запуска космических ракет на орбиту Земли. Поэтому космодромы располагают как можно ближе к Экватору, где вес ракеты меньше. Если же не учитывать влияние сплюснутости Земли (≈0,2%), то ускорение силы тяготения на полюсе:  А на экваторе:  Для обычных расчетов обычно принимается определенное стандартное ускорение:  Действие центробежной силы инерции широко используют в технике: в центробежных насосах, сепараторах, центробежном регуляторе и т. д. При проектировании быстро вращающихся деталей машин - роторов турбин, компрессоров, электрических двигателей, двигателей внутреннего сгорания, винтов самолетов и вертолетов принимаются специальные меры для уравновешивания центробежных сил инерции. Например, в случае деталей, симметричных относительно оси вращения, производят их тщательную статическую и динамическую балансировку, так как малейшее смещение центра масс в сторону от оси вызывает при быстром вращении детали столь большие дополнительные нагрузки на ее подшипники, что они быстро разрушаются. В случае несимметричных деталей, например коленчатых валов, применяют специальные противовесы. При расчете на прочность быстро вращающихся деталей машин учет центробежных сил инерции совершенно необходим, так как эти силы но многих случаях играют определяющую роль. Кориолисова сила инерции Эта сила действует на материальную точку только тогда, когда неинерциальная система отсчета вращается, а материальная точка движется относительно нее. Кориолисова сила инерции не совершает работы в относительном движении материальной точки, так как эта сила направлена перпендикулярно скорости относительного движения точки. Следовательно, Кориолисова сила инерции служит примером гироскопических сил Силы инерции реально действуют на материальную точку в неинерциальной системе отсчета и могут быть в ней измерены, например с помощью пружинного динамометра. Сила Кориолиса одна из сил инерции, существующая во вращающейся системе отсчёта и проявляющаяся при движении в направлении под углом к оси вращения. Сила Кориолиса равна:  где m - точечная масса, - вектор угловой скорости, - вектор скорости движения точечной массы. Причина появления силы Кориолиса - в Кориолисовом ускорении. Для того, чтобы тело двигалось с Кориолисовым ускорением, необходимо приложение силы к телу, равной F = ma, где a - Кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности. F= − ma. Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции - центробежной силой, которая направлена по радиусу вращающейся окружности. В инерциальных системах отсчёта действует закон инерции, т.е каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса. Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки - то вправо. Сила Кориолиса проявляется в работе маятника Фуко. Маятник Фуко является математическим маятником, такой маятник, отклонённый от равновесного положения, совершает колебания в плоскости, неподвижной в инерциальной системе отсчёта (в данном случае - системе отсчёта, «связанной» со звёздами). Наблюдатель, находящийся на Земле и вращающийся вместе с нею, находится в неинерциальной (вращающейся) системе отсчёта и будет видеть, что плоскость колебаний маятника медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли. На Северном или Южном полюсе Земли (ось вращения Земли лежит в плоскости колебаний маятника) плоскость колебаний маятника Фуко совершает поворот на 360° за звёздные сутки (на 15° за звёздный час), на экваторе (ось вращения Земли перпендикулярна плоскости колебаний маятника) плоскость колебаний маятника Фуко неподвижна Кроме того, поскольку Земля вращается, то сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в северном полушарии более крутые - их подмывает вода под действием этой силы (закон Бэра - правило, согласно которому в северном полушарии реки, текущие в меридиональном направлении, подмывают правый берег, в южном полушарии - левый). Объясняется Кориолисовой силой, действующей на воду при её удалении от (приближении к) оси вращения Земли). В южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за возникновение циклонов и антициклонов. А также она приводит к наличию дополнительного бокового давления на рельсы, а, следовательно, их неравномерный износ, возникающих при движении поездов. Вопреки расхожему мнению, маловероятно, что сила Кориолиса полностью определяет направление закручивания воды в водопроводе - например, при сливе в раковине. Хотя в разных полушариях она действительно стремится закручивать водяную воронку в разных направлениях, при сливе возникают и побочные потоки, зависящие от формы раковины и конфигурации канализационной системы. По абсолютной величине создаваемые этими потоками силы превосходят силу Кориолиса, поэтому направление вращения воронки как в северном, так и в южном полушарии может быть как по часовой стрелке, так и против неё. 6. Релятивистская динамика Преобразование импульса и энергии В релятивистской динамике, так же как и в классической механике, импульс тела определяется как произведение массы на скорость. Но из условия, что фундаментальный закон сохранения импульса должен исполняться в любой инерциальной системе отсчета, выплывает, что (в отличии от классической механики) масса частицы зависит от ее скорости: (1) |