Реферат Кинематика. Махметова А.Ш. Задание 1. Кинематика и динамика материальной точ. Кинематика и динамика материальной точки. Динамика твердого тела

• Название: Кинематика и динамика материальной точки. Динамика твердого тела
• Анкор: Реферат Кинематика
• Дата: 20.10.2021
• Размер: 0.59 Mb.
• Имя файла: Махметова А.Ш. Задание 1. Кинематика и динамика материальной точ.docx
• Тип: Реферат; #251980
• страница: 1 из 4

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

АКАДЕМИЯ ГРАЖДАНСКОЙ АВИАЦИИ

КАФЕДРА «СОЦИАЛЬНО-ГУМАНИТАРНЫХ ДИСЦИПЛИН»





Реферат

На тему:«Кинематика и динамика материальной точки. Динамика твердого тела»

Преподаваетель: Беркутбаева Р. А.

Выполнил(a): студентка группы УВД-ОАП-21-2

Махметова А.Ш.

Алматы, 2021

Содержание:

1. 
   Кинематика.
   

2. 
   Динамика.
   

3. 
   Закон сохранения импульса и момента импульса .
   

4. 
   Работа и кинетическая энергия вращающегося тела.
   

5. 
   Движение в уентральном поле.
   

6. 
   Релятивисткая динамика.
   

1. Кинематика
Вывод формулы для нормального и тангенциального ускорения

При любом движении точки, кроме равномерного прямолинейного движения, скорость точки изменяется. Для характеристики быстроты изменения скорости точки в механике вводится векторная физическая величина, называемая ускорением.

Ускорением называется вектор а, равный первой производной по времени t от скорости этой точки;

Ускорение точки равно также второй производной по времени от радиус-вектора r этой точки:

Поскольку вектор ускорения при криволинейном движении сориентирован по отношению к скорости под произвольным углом, то разложим его на нормальную и тангенциальную составляющие:

Определим величину, направление и роль в изменении скорости нормального ускорения. Предположим, что:

= a_n.
Тогда:

= a·dt = a_n·dt.
Таким образом, вектор приращения скорости параллелен вектору нормального ускорения. Поскольку нормаль n перпендикулярна , а, следовательно, и вектору скорости, то всегда вектор приращения скорости также перпендикулярен v. В данном случае годограф представляет из себя окружность, и скорость изменяется только по направлению, сохраняясь неизменной по величине. Следовательно, направление вектора приращения скорости совпадает с вектором n.

Величину вектора a_n можно рассчитать из простых геометрических соображений.

Следовательно, в данном случае вектор приращения скорости параллелен вектору тангенциального ускорения. Вектора приращения скорости и тангенциального ускорения также направлены вдоль

Тангенциальное ускорение характеризует изменение скорости по величине. Вектор тангенциального ускорения равен

В общем случае, когда скорость изменяется по величине и направлению значение модуля вектора ускорения равно: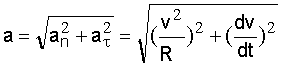
.
Сам вектор полного ускорения состоит из суммы двух слагаемых:

Нормальное ускорение точки характеризует быстроту изменения направления вектора скорости точки. Нормальное ускорение направлено всегда к центру кривизны траектории, так что его проекция на главную нормаль n не может быть отрицательной:

По этой причине нормальное ускорение точки часто называют также центростремительным ускорением. Нормальное ускорение точки равно нулю только в том случае, если точка движется прямолинейно.

Движение по окружности. Угловой путь, угловая скорость, угловое ускорение

При вращении твердого тела вокруг неподвижной оси все его точки движутся по окружностям, центры которых лежат на оси вращения, а плоскости окружностей перпендикулярны к ней. Точки тела, находящиеся на разных расстояниях от оси вращения, движутся по разным окружностям и в связи с этим все кинематические характеристики разных точек тела будут разными:

Но положение тела полностью определяется заданием угла поворота из некоторого начального положения. В этом случае говорят, что тело имеет одну степень свободы.

Рассмотрим движение точки, вращающейся вокруг оси, более подробно (рис 1).Передвигаясь по траектории, точка проходит путь и поворачивается на определенный угол . По аналогии пути вводят понятие углового пути , который равен углу поворота тела за время и направленный вдоль оси вращения так, что если смотреть вдоль него, то поворот тела наблюдается происходящим по часовой стрелке.

При рассмотрении движения материальной точки, использовался вектор перемещения 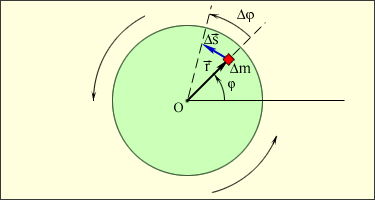, который является основой математического описания движения. По аналогии, для описания вращательного движения вводят понятие углового перемещения или вектора углового перемещения , являющейся аксиальным вектором (всегда направлены вдоль оси вращения).


Рис. 1
Следующей кинематической характеристикой вращательного движения есть угловая скорость - скорость изменения угла поворота, которая равна первой производной угла поворота по времени:

Это, конечно, мгновенная угловая скорость. Она направлена по оси вращения в соответствии с правилом буравчика или правого винта.

Если угловая скорость постоянна, то для характеристики движения часто вводят понятие периода вращения Т, т.е. времени, за которое тело совершает полный оборот, . Период связан с угловой скоростью формулой:

Число оборотов n, совершенное телом за единицу времени - частота. Это величина, обратная периоду:

Угловое ускорение - быстрота изменения угловой скорости с течением времени, равно первой производной угловой скорости и направлено вдоль оси вращения или равно второй производной по углу поворота:

Угловое ускорение - вектор, направленный по оси вращения. Он совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном.

2. 
   Динамика
   

Следствия из преобразования Галилея. Инварианты преобразований (инвариантность длины, времени, ускорении, уравнений Ньютона)

Как известно, описывать движение можно только в том случае, если задана система отсчета. Но систем отсчета существует множество, и в каждой из них характеристики одного и того же самого движения могут принимать разные значения. Поэтому, необходимо уметь переходить с одной системы отсчета в другую. При этом будем считать, что при рассмотрении небольших скоростей ( «c) справедливы законы классической механики. Когда речь идет о скоростях приближающихся к скорости света, справедливы законы специальной теории относительности (релятивистской механики).

Покажем, что законы механики Ньютона имеют одинаковый вид в двух инерциальных системах К и К’, движущихся относительно друг друга со скоростью U (рис. 2) Положение движущейся точки массой m относительно первой системы зададим радиус-вектором 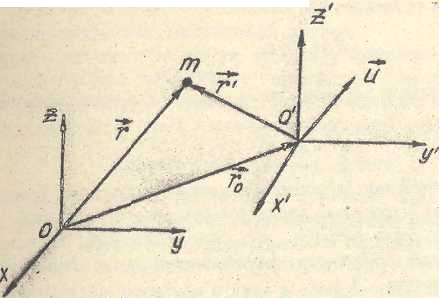, относительно второй - .


Рис, 2
Из рисунка видно, что связь между и следующая: (1)
(1)
Запишем ее для каждой координаты в отдельности: (2)

Эти формулы позволяют определить координаты материальной точки в системе К, если известны ее координаты в системе . Обратный переход: (3)

Такие уравнения называются преобразованиями координат Галилея. Они дают возможность вычислить координаты движущейся точки по отношению к системе К, если известны координаты ее в системе , и наоборот.

Связь скоростей точки и в разных системах получим, продифференцировав по времени формулу (1),

или (4)

Если в одной из инерциальных систем отсчета тело двигалось с постоянной скоростью , то и в другой оно также будет иметь постоянную скорость . Значит первый закон динамики будет выполняться в обеих системах отсчета.

Поскольку система К движется относительно системы К’ с постоянной скоростью, , то

т.е. ускорения в обеих системах одинаковы, а так как масса движущейся точки m не изменилась при переходе в другую систему, то второй закон динамики будет иметь такой же вид, как и в первой системе: (5)

Таким образом, законы классической механики инвариантны по отношению к преобразованиям Галилея.

В рассматриваемом случае длина отрезка и интервал времени не зависит от системы отсчета, т.е. если мы измерим в системе К длину какого-то предмета, то она будет точно такой в системе Аналогичное заключение можно сделать и относительно интервала времени между событиями, т.e. длина и время тоже инвариантны по отношению к преобразованиям Галилея.

2. 
   Закон сохранения импульса и момента импульса
   

Центр инерции. Аддитивность массы.

Центр масс системы материальных точек - точка, положение которой характеризует распределение массы системы в пространстве. Центр масс - это точка приложения внешних сил, действующих на систему, движущуюся таким образом, как будто суммарная масса системы тел сосредоточена в этой точке.

Аддитивность - свойства физических, геометрических и других величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разделении объекта на части: аддитивность массы тела означает, что масса тела равна сумме масс составляющих его частей.

Координаты центра масс системы тел определяются следующим образом: (1)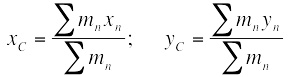

где и - массы и соответствующие координаты тел, входящих в систему.

Положение центра масс тела зависит от того, как распределяется по объему тела его масса. Центр масс не обязательно должен находиться в самом теле. Если тело движется поступательно под действием нескольких сил, значит, точка приложения равнодействующей этих сил находится в центре масс этого тела. Если направление прямой, вдоль которой действует сила, не проходит через центр масс тела, эта сила вызывает поворот тела.

При поступательном движении тела все его точки движутся с таким же ускорением, которое получает центр масс этого тела под действием равнодействующей внешних сил. Следовательно, для того чтобы описать поступательное движение тела, необходимо описать движение центра масс этого тела под действием равнодействующей внешних сил. При движении тела (механической системы) его центр масс движется так же, как двигалось бы под действием равнодействующей внешних сил материальная точка, имеющая массу, равную массе тела (системы). Поэтому, когда мы считаем тело материальной точкой, то имеем в виду центр масс данного тела.

Скорость центра масс механической системы равна отношению импульса этой системы к ее массе: (2)


Соответственно импульс системы равен произведению ее массы на скорость центра масс: . Подставив это выражение для р в уравнение получим закон движении центра масс: (3)

Теорема о движении центра масс системы. Закон сохранения центра массы

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил (центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору приложенных к системе внешних сил).

Этот закон показывает, что для изменения скорости центра масс системы необходимо, чтобы на систему действовала внешняя сила. Внутренние силы взаимодействия частей системы могут вызывать изменения скоростей этих частей (например, при разрыве снаряда на несколько осколков), но они не могут повлиять на суммарный импульс системы и скорость ее центра масс.

Из закона движения центра масс следует, что скорость центра масс замкнутой механической системы не изменяется с течением времени. Иными словами, центр масс замкнутой системы либо покоится, либо движется с постоянной скоростью относительно неинерциальной системы отсчета.

В качестве системы отсчета в механике часто пользуются системой центра масс поступательно движущейся системы отсчета, относительно которой центр масс рассматриваемой механической системы неподвижен. Из сказанного выше ясно, что система центра масс замкнутой механической системы инерциальная.

Закон сохранения движения центра масс.

Если главный вектор (векторная сумма) внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно.

2. 
   Работа и кинетическая энергия вращающегося тела.
   

Кинетическая энергия твердого тела складывается из кинетических энергий его частей Ei. Рассчитаем значение Ei для элементов твердого тела.

_i = m_i·v_i²/2 = m_i·w²·r_i²/2.
Кинетическая энергия твердого тела будет равна:

_к = w²/2·m_i·r_i² = I·w²/2. (8.13)
Заметим, что формула для расчета Eк похожа на выражение для определения кинетической энергии поступательного движения тела, только роль меры инертности в этом случае играет момент инерции, а не масса и характеристикой движения является угловая, а не линейная скорость твердого тела. Можно показать, что при произвольном движении твердого тела его кинетическая энергия Wt равна сумме кинетической энергии поступательного движения тела со скоростью v_c его центра масс и кинетической энергии вращения тела с угловой скоростью вокруг мгновенной оси, проходящей через центр масс

Рассчитаем работу силы, вызывающей вращательное движение тела вокруг некоторой оси и приложенной к произвольной точке этого тела.

При вращательном движении твердого тела под действием силы F работа равняется произведению момента этой силы на угол поворота.

Работа переменной силы при повороте тела на конечный угол равняется определенному интегралу от момента сил:
.

кинематический динамический точка тело

2. 
   Движение в центральном поле
   

Центральная сила - сила, которая всегда направлена по радиус-вектору, соединяющему материальную точку с некоторой точкой в пространстве, и зависит только от расстояния до этой точки (pис.