Классификация вычислительных приемов. Классификация вычислительных приемов. Методы работы педагога по. Классификация вычислительных приёмов
 Скачать 438.32 Kb. Скачать 438.32 Kb.
|
|
Классификация вычислительных приемов. Методы работы педагога по формированию вычислительного навыка Формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе. Эти навыки должны формироваться осознанно и прочно, так как на их базе строится весь начальный курс обучения математике. В начальных классах особое место занимает работа по формированию навыков устных вычислений, поскольку в течение четырех лет обучения учащиеся должны не только сознательно усвоить приемы устных вычислений, но и приобрести твердые вычислительные навыки. Устные вычисления способствуют лучшему усвоению приемов письменных вычислений. т.к. последние включают в себе элементы устных вычислений. Общеизвестно, что теоретической основой вычислительных приемов служат определения арифметических действий, свойства действий, и следствия, вытекающие из них. Имея это в виду можно выделить группы приемов вычислительных навыков в соответствии с их общей теоретической основой предусмотренной действующей программой по математике для начальных классов, что даст возможность использовать общие подходы в методике формирования соответствующих навыков. Вычислительный приём – это система операций, последовательное выполнение которых приводит к результату действия. Различают операции основные и вспомогательные. Основными называют операции, сразу дающие результат. Вспомогательными называют операции, которые лишь готовят к выполнению действия. Теоретической основой вычислительных приёмов служат определения арифметических действий, свойства действий и следствия, вытекающие из них. Имея это в виду и принимая во внимание методический аспект, можно выделить группы приёмов в соответствии с их общей теоретической основой. Классификация вычислительных приёмов. 1. Приемы, теоретическая основа которых — конкретный смысл арифметических действий. К ним относятся: приемы сложения и вычитания чисел в пределах 10 для случаев вида а + 2, а + 3, а + 4, а + 0; приемы табличного сложения и вычитания с переходом через десяток в пределах 20; прием нахождения табличных результатов умножения, прием нахождения табличных результатов деления. 2. Приемы, теоретической основой которых служат свойства арифметических действий. К этой группе относится большинство вычислительных приемов. Это приемы сложения и вычитания для случаев вида 53 ± 20, 47 ± 3, 30 – 6, 9 + 3, 12 – 3, 35 ± 7, 40 ± 23, 57 ± 32, 64 ± 18; аналогичные приемы для случаев сложения и вычитания чисел больших, чем 100, а также приемы письменного сложения и вычитания; приемы умножения и деления для случаев вида 14 × 5, 5 × 14, 81 : 3, 18 Ч 40, 180 : 20, аналогичные приемы умножения и деления для чисел больших 100 и приемы письменного умножения и деления. Общая схема введения этих приемов одинакова: сначала изучаются соответствующие свойства, а затем на их основе вводятся приемы вычислений. 3. Приемы, теоретическая основа которых — связи между компонентами и результатами арифметических действий. К ним относятся приемы для случаев вида 9 × 7, 21 : 3, 60 : 20, 54 : 18, 9 : 1, 0 : 6. При введении этих приемов сначала рассматриваются связи между компонентами и результатом соответствующего арифметического действия, затем на этой основе вводится вычислительный прием. 4. Приемы, теоретическая основа которых — изменение результатов арифметических действий в зависимости от изменения одного из компонентов. Это приемы округления при выполнении сложения и вычитания чисел (46 + 19, 512 – 298) и приемы умножения и деления на 5, 25, 50. Введение этих приемов также требует предварительного изучения соответствующих зависимостей. 5. Приемы, теоретическая основа которых — вопросы нумерации чисел. Это приемы для случаев вида а ± 1, 10 + 6, 16 – 10, 16 – 6, 57 Ч 10, 1200 : 100; аналогичные приемы для больших чисел. Введение этих приемов предусматривается после изучения соответствующих вопросов нумерации (натуральной последовательности, десятичного состава чисел, позиционного принципа записи чисел). 6. Приемы, теоретическая основа которых — правила. К ним относятся приемы для двух случаев: а × 1, а × 0. Поскольку правила умножения чисел на единицу и нуль есть следствия из определения действия умножения целых неотрицательных чисел, то они просто сообщаются учащимся и в соответствии с ними выполняются вычисления. В век компьютерной грамотности значимость навыков письменных вычислений, несомненно, уменьшилась. Вместе с тем, научиться быстро и правильно выполнять письменные вычисления важно для младших школьников как в плане продолжающейся работы с числами, так и в плане практической значимости этих навыков для дальнейшего обучения в школе. Приоритетными задачами в развитии российского образования являются формирование у учащихся личностных качеств, а также универсальных учебных умений, а также и способностей к самостоятельной учебной деятельности. Формирование у младших школьников вычислительных навыков остаётся одной из главных задач начального обучения математике, поскольку вычислительные навыки необходимы при изучении арифметических действий. Вычислительный навык – это высокая степень овладения вычислительными приёмами, это вычислительный приём, доведенный до автоматизма. Приобрести вычислительный навык – значит, для каждого случая знать какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро. В качестве сформированности полноценного вычислительного навыка можно выделить следующие критерии: правильность; осознанность; рациональность; обобщённость; автоматизм; прочность. О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции приводящие к решению. Формирование всякого вычислительного навыка включает в себя ряд этапов: I – подготовительный этап; II – ознакомление с новым вычислительным приемом; III – усвоение вычислительного приема и формирование вычислительного умения и навыка. В процессе работы важно предусмотреть ряд стадий в формировании у учащихся вычислительных навыков. На первой стадии закрепляется знание приема: учащиеся самостоятельно выполняют все операции, составляющие прием, комментируя выполнение каждой из них вслух и одновременно производя развернутую запись, если она была предусмотрена на предыдущем этапе. На второй стадии происходит частичное свертывание выполнения операций: учащиеся про себя выделяют операции, обосновывают выбор и порядок их выполнения, вслух же они проговаривают выполнение основных операций, то есть промежуточных вычислений. На третьей стадии происходит полное свертывание выполнения операций: учащиеся про себя выделяют и выполняют все операции, то есть здесь происходит свертывание и основных операций. Четвертая стадия характеризуется предельным свертыванием выполнения операций: учащиеся выполняют все операции в свернутом плане предельно быстро, то есть они овладевают вычислительными навыками. Это достигается в результате выполнения достаточного числа тренировочных упражнений. Названные стадии не имеют четких границ: одна постепенно переходит в другую. Выбирая методы работы по формированию вычислительных навыков на уроках математики, перед учителями встаёт вопрос, как сделать привычную и, казалось бы, однообразную работу эффективной, а значит интересной и увлекательной. Именно это и заставляет учителей постоянно придумывать что-то новое, совершенствовать уже известное. Решению указанных задач способствует применение в образовательном процессе технологии деятельностного метода, благодаря которому учитель имеет возможность на уроках независимо от их предметного содержания организовывать выполнение учащимися всего комплекса УУД, определенных ФГОС. При деятельностном подходе к обучению главная задача учителя – не «донести», «преподнести» и показать учащимся, а организовать совместный поиск решения, возникший перед ними задачи. Теперь процесс обучения представляет собой сложную динамическую систему, в которой в органичном единстве происходит взаимосвязанная деятельность учителя и ученика. В этой системе под руководством учителя учащиеся овладевают основами наук, способами деятельности и рациональными приемами работы. Задача учителя состоит не только в том, чтобы сообщать знания, а и управлять процессом усвоения знаний и способов деятельности. Задача ученика- овладевать системой знаний, способами их приобретения, переработки, сохранения и применения, воспитывая в себе необходимые качества личности. За основную структурную единицу процесса мышления принимается действие. Действие, как единица анализа деятельности учащегося. Учитель должен уметь не только выделять действия, которые входят в разные виды познавательной деятельности учащихся, но и найти их структуру, функциональные части, основные свойства и закономерности их становления. Избежать быстрой утомляемости и снижения внимания при выполнении вычислений поможет чередование различных видов деятельности, отказ от однообразных тренировочных упражнений, обучение приёмам действия контроля. Действие контроля должно присутствовать на каждом этапе выполнения вычислительного приёма. Только в этом случае возможно постоянное прослеживание хода выполнения учебных действий, своевременное обнаружение различных больших и малых погрешностей в их выполнении, а также внесение необходимых корректив в них. Обнаруженная ошибка в процессе вычислений позволит сохранить ребёнку внутренние силы, предотвратить преждевременную усталость. Для контроля в выполнении письменных вычислений целесообразно показать ученикам, как использовать опорные сигнал, например точки, напоминающие о том, что следует учесть перенесённую через разряд единицу. В связи с этим необходимо больше внимания уделять формированию действия контроля в процессе работы над вычислительными приёмами и навыками, так как организационное на уроке математики действие контроля, приводит к концентрации внимания всех учащихся, формирует в практической деятельности каждого ученика умение рассуждать, исключает ошибки в тетрадях, что позволяет совершенствовать умения осознанно выполнять вычислительные приёмы. Присутствие в вычислительных упражнениях элемента занимательности, игры, догадки, сообразительности, использование интересного наглядного материала – вот те основные приёмы активизации познавательной деятельности, реализация которых позволит решить в практике обучения и задачу формирования прочных вычислительных навыков, и задачу развития познавательных способностей учащихся. Использование на уроках математики заданий различного типа возбуждает у детей интерес, стимулирует их к активной деятельности и позволяет более прочно сформировать вычислительные навыки. !!!!!!! Классификация вычислительных приёмов. 1. Вычислительные приёмы, основанные на знании нумерации: - на знании последовательности натурального ряда чисел; (например, 5 + 1; 600 - 1); - на знании разрядного состава; (например, 54 - 50; 600 + 50); - на понятиях увеличить или уменьшить в 10; 100; 1000 и т. д. раз. (например, 5 × 10; 900 : 100). 2. Вычислительные приёмы, основанные на знании конкретного смысла арифметических действий: - сложение и вычитание по частям однозначных чисел; (например,5 + 2; 7 - 3); - сложение и вычитание с переходом через десяток; (например, 8 + 7; 12 - 5); - составление первого столбика таблицы умножения; (например, 8 × 8; 8 × 9). Конкретный смысл деления раскрывается на решении простых задач. 3. Вычислительные приёмы, основанные на знании взаимосвязей между результатом и компонентами арифметических действий: - вычитание вида «9 – а, 8 – а, 7 – а, 6 – а»; (например, 9 – 6; 8 – 5); - вычитание вида «12 - 5»; - составление третьего столбика на деление таблицы умножения; (например, 54 : б; 49 : 7); - деление двузначного числа на двузначное; (например, 51 : 17; 54 : 27). 4. Вычислительные приёмы, основанные на знании свойств арифметических действий: - переместительного закона сложения; (вида «а + 5, а + б, а + 7, а + 8, а + 9». Например, 8 + 6); -прибавления числа к сумме; (например, 34 + 2; 34 + 20); - прибавления суммы к числу; (например, 48 + 9; 42 + 15); - вычитания числа из суммы; (например, 34 – 2; 34 – 20); - вычитания суммы из числа; (например, 62 – 9; 95 – 12); -переместительного закона умножения; (например, 4 × 6; 5 × 9); - умножение суммы на число; (например, 27 × 3; 24 × 4); - деление суммы на число; (например, 54 : 3; 96 : 2); - умножение числа на сумму; (например, 54 × 12); - умножение числа на произведение; ( например. 38 × 20; 42 × 30); - деление числа на произведение; (например,620 : 20; 840 : 30). 5. Вычислительные приёмы, основанные на знании частных случаев выполнения арифметических действий с числами 1 и 0; (например, 84 : 1; 62 × 0). Формирование у младших школьников вычислительных навыков остаётся одной из главных задач начального обучения математике, поскольку вычислительные навыки необходимы при изучении арифметических действий. Этапы формирования вычислительных навыков Формирование у младших школьников вычислительных навыков остаётся одной из главных задач начального обучения математике, поскольку вычислительные навыки необходимы при изучении арифметических действий. Вычислительный навык – это высокая степень овладения вычислительными приёмами, это вычислительный приём, доведенный до автоматизма. Приобрести вычислительный навык – значит, для каждого случая знать какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро. В качестве сформированности полноценного вычислительного навыка можно выделить следующие критерии: - правильность; - осознанность; - рациональность; - обобщённость; - автоматизм; - прочность. О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции приводящие к решению. Формирование всякого вычислительного навыка включает в себя ряд этапов: I – подготовительный этап; II – ознакомление с новым вычислительным приемом; III – усвоение вычислительного приема и формирование вычислительного умения и навыка. Рассмотрим особенности каждого из этапов. 1. Подготовка к введению нового приема. На этом этапе создается готовность к усвоению вычислительного приема, а именно: учащиеся должны усвоить те теоретические положения, на которых основывается теоретический прием. Центральное же звено при подготовке к введению нового приема – овладение учеником основными операциями, которые войдут в новый прием. 2. Ознакомление с вычислительным приемом. На этом этапе ученики усваивают суть приема: какие операции надо выполнять, в каком порядке и почему именно так можно найти результат арифметического действия. Степень самостоятельности учащихся должна увеличиваться при переходе от приема к приему другой группы. 3. Закрепление знания приема и выработка вычислительного навыка. На данном этапе учащиеся должны твердо усвоить систему операций, составляющих вычислительный прием, и предельно быстро выполнять эти операции, то есть овладеть вычислительным навыком. В процессе работы важно предусмотреть ряд стадий в формировании у учащихся вычислительных навыков. На первой стадии закрепляется знание приема: учащиеся самостоятельно выполняют все операции, составляющие прием, комментируя выполнение каждой из них вслух и одновременно производя развернутую запись, если она была предусмотрена на предыдущем этапе. На второй стадии происходит частичное свертывание выполнения операций: учащиеся про себя выделяют операции, обосновывают выбор и порядок их выполнения, вслух же они проговаривают выполнение основных операций, то есть промежуточных вычислений. На третьей стадии происходит полное свертывание выполнения операций: учащиеся про себя выделяют и выполняют все операции, то есть здесь происходит свертывание и основных операций. Четвертая стадия характеризуется предельным свертыванием выполнения операций: учащиеся выполняют все операции в свернутом плане предельно быстро, то есть они овладевают вычислительными навыками. Это достигается в результате выполнения достаточного числа тренировочных упражнений. Названные стадии не имеют четких границ: одна постепенно переходит в другую. Задания, направленные на формирование вычислительных навыков в начальной школе На уроке математики формирование вычислительных навыков занимает большое место. Овладение вычислительными навыками имеет большое образовательное, воспитательное и практическое значение: —образовательное значение: устные вычисления помогают усвоить многие вопросы теории арифметических действий, а также лучше понять письменные приемы; —воспитательное значение: устные вычисления способствуют развитию мышления, памяти, внимания, речи, математической зоркости, наблюдательности и сообразительности; —практическое значение: быстрота и правильность вычислений необходимы в жизни, особенно когда письменно выполнить действия не представляется возможным (например, при технических расчетах у станка, в поле, при покупке и продаже). В своей работе учителя придерживаются определенных принципов. Один из них (наиболее важный) можно сформулировать следующим образом: работа в классе на каждом уроке должна выполняться всем классом, а не учителем и группой успевающих учеников. То есть необходимо создать такую ситуацию — ситуацию «успеха», при которой каждый ученик смог бы почувствовать себя полноценным участником учебного процесса. Ведь одна из задач учителя заключается не в доказательстве незнания или слабого знания ученика, а во вселении веры в ребенка, что он может учиться лучше, что у него получается. Нужно помочь ребенку поверить в собственные силы, мотивировать его на учебу. Одной из форм работы по формированию вычислительных навыков являются задания разных типов. Рассмотрим основные типы заданий: 1.Задания с использованием сравнений: Для активизации познавательной деятельности учащихся при формировании вычислительных можно использовать метод наблюдений. В процессе наблюдения учащиеся сравнивают, анализируют, делают выводы. Полученные таким образом знания являются более осознанными и тем самым лучше усваиваются. В качестве примера рассмотрим изучение такого вопроса, как изменение суммы в зависимости от изменения одного из слагаемых. В основе познания учениками данной зависимости лежит прием сравнения. Задание 1. Решите примеры и сравните их: 40 × 2, 40 × 4. Необходимо обращать внимание учеников на то, что в одном и в другом примере стоит знак « × », а первые множители одинаковы. Эти примеры схожи. Затем выявляются различия: в первом примере второй множитель равен 2, во втором 4, произведениев первом примере равно 80, а во втором – 160. Ребята отмечают, что во втором примере умножаем большее (4 > 2), поэтому и получаем большее произведение. Переходя к сравнению выражений подбираем такие выражения, в которых ученики смогут усмотреть различные признаки различия и сходства. Задание 2. На доске записаны примеры: 5 × 3, 7 × 3, 8 × 3, 24 : 3, 12 : 3, 6 : 3, Найдите сходство или различие записанных выражений. Ученики обычно указывают такие признаки сходства, как знак действия, затем обращают внимание на то, что в первой группе умножается число на 3, а во второй – делится число на 3. Затем целесообразно поставить вопрос: «Что произойдет с ответами примеров в первой группе и во второй? Почему ответы в первой группе больше, чем ответы во второй?» Очень полезно задание и такое: Задание 3. Что вы замечаете в данных примерах? 2 × 8, 3 × 8, 4 × 8, 6 × 8, 7 × 8, 8 × 8 Ученики должны обратить внимание не только на тот факт, что во всех примерах знак « × » и второе слагаемое везде равно 8, но и на то, что последовательность 2, 3, 4, … нарушена, т.к. пропущен пример 5 + 8. Подобные задания способствуют развитию математической наблюдательности учеников, их умению видеть сходства и различия, выявлять определенные закономерности. В процессе выполнения таких заданий уясняется смысл понятия « сравнить ». Так же могут предлагаться задания с ошибками, которые требуют исправления. Задание « Найди ошибку»: могут предлагаться задания, у которых уже дан знак отношения и одно из выражений, а другое выражение надо составить или дополнить: 8 · (10 : 2)=8 · 10 × …Выражения таких заданий могут включать различный числовой материал: однозначные, двузначные, трехзначные числа и величины. Выражения могут быть с разными действиями. Главная роль таких заданий – способствовать усвоению теоретических знаний об арифметических действиях, их свойствах, о равенствах, о неравенствах и др. Также они помогают выработке вычислительных навыков. 2.Задания на классификацию и систематизацию знаний. Умение выделять признаки предметов и устанавливать между ними сходство и различие — основа заданий на классификацию. Из курса математики известно, что при разбиении множества на классы необходимо выполнять следующие условия: 1) ни одно из подмножеств не пусто; 2) подмножества попарно не пересекаются; 3) объединение всех подмножеств составляет данное множество. Предлагая детям задания на классификацию, эти условия необходимо учитывать. 3.Задания на выявление общего и различного. Выделение существенных признаков математических объектов, их свойств и отношений — основная характеристика таких заданий. Благодаря им учащиеся могут самостоятельно «открывать» математические свойства и способы действий (правила), которые в математике строго доказываются. Задание 1. Рассмотрите рисунок и попробуйте быстро подсчитать, сколько окон в доме.  Дети могут предложить следующие способы: 3+3+3+3, 4+4+4 или 3 × 4 = 12; 4 × 3 = 12. Учитель предлагает сравнить полученные равенства, т. е. выявить их сходство и различие. Отмечается, что оба произведения одинаковые, а множители переставлены. Вывод: « Если множители переставить, то произведение не изменится » или « От перестановки множителей значение произведения не изменится ». 4.Задания с многовариантными решениями. Многовариантные задания — это система упражнений, выполнение которых поможет глубоко и осознано усвоить правило и выработать необходимый вычислительный навык на его основе. Задание 1. Запиши число 30 тремя одинаковыми цифрами и знаками действий. Постарайся найти несколько разных решений. Задание 2. Какое число надо прибавить к 25, чтобы получить круглое? 5.Задания с элементами занимательности. Такие задания, в основном, направлены на отработку вычислительных навыков. Элемент занимательности увлекает детей, они стремятся выполнить все действия правильно и посмотреть к чему это приведет. «Магические или занимательные квадраты» — это занимательная форма тренировки в сложении вычитания и размещения чисел. Решение магических квадратов увлекает школьников всех возрастов. 6.Задания на нахождение значений математических выражений. Предлагается в той или иной форме математическое выражение, требуется найти его значение. Эти задания имеют много вариантов. Можно предлагать числовые математические выражения и буквенные (выражение с переменной), при этом буквам придают числовые значения и находят числовое значение полученного выражения, например: — найдите частное чисел 40 и 8.- найдите значение выражения С × К, если С = 40, К = 8. Выражения могут предлагаться в разной словесной форме: 40 × 8; 40 умножить на 8 – делимое 40, делитель 8, найдите частное чисел 40 и 8 – делить 40 на 8 и т.д. Эти формулировки использует не только учитель, но и ученики. Выражения могут быть даны с ошибками, которые детям предстоит найти: Задание 1. Найди ошибки в выражениях: 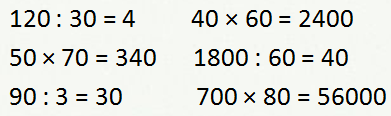 Выражения могут включать одно и более действий. Выражения с несколькими действиями могут включать действия одной ступени или разных ступеней, например: 47 + 24 – 56 72: 12 · 9 400 – 7 · 4 и др. Могут быть со скобками или без скобок: (90 – 42): 3, 90 – 42: 3. Как и выражения в одно действие, выражения в несколько действий имеют разную словесную формулировку, например: из 90 вычесть частное чисел 42 и 3 – уменьшаемое 90, а вычитаемое выражено частным чисел 42 и 3. Выражения могут быть заданы в разной области чисел: с однозначными числами (7 – 4), с двузначными (70 – 40, 72 – 48), с трехзначными (700 – 400, 720 – 480) и т. д., с натуральными числами и величинами (200 – 15, 25 м – 15 см). Однако, как правило, приёмы устных вычислений должны сводиться к действиям над числами в пределах 100. Так, случай вычитания четырехзначных чисел 7200 – 4800 сводится к вычитанию двузначных чисел (72 сотни – 48 сотен) и значит его можно предлагать для устных вычислений. Выражения можно давать и в форме таблицы: Задание 2. Заполни таблицы:  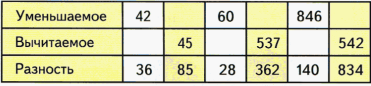 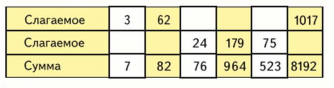 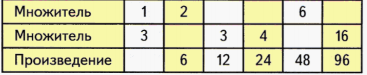 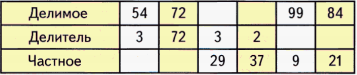 Так же такие задания могут быть представлены в виде раз личных «цепочек»: Задание 3: Реши цепочки: 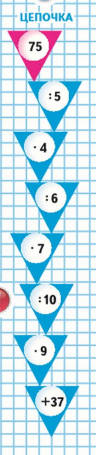 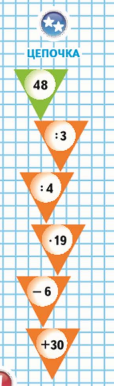  Основное значение заданий на нахождение значений выражений – выработать у учащихся твердые вычислительные навыки, а также они способствуют усвоению вопросов теории арифметических действий. 7.Комбинаторные задачи. Комбинаторика — один из разделов современной математики. Комбинаторные задачи служат средством развития мышления детей, воспитания у них умения применять полученные знания в различных ситуациях посредством выработки навыков и повторения пройденного. Умение выполнять разбиение множеств, составлять комбинации по определенным признакам и классифицировать лежит в основе разнообразных сфер человеческой деятельности. Задание 1. При умножении двух однозначных чисел получилось число 16 Чему были равны множители? Найди всевозможные решения. Задание 2. На складе находилось 7 полных бочонков меда, 7 наполовину заполненных медом и 7 пустых бочонков. Как распределить все бочонки между тремя покупателями так, чтобы каждый получил одинаковое количество меда и бочонков. (мед не нужно перекладывать из одного бочонка в другой.) Использование на уроках математики заданий различного типа возбуждает у детей интерес, стимулирует их к активной деятельности и позволяет более прочно сформировать вычислительные навыки. |
