Шпаргалка по физике УрФУ. Кластер с014 п графические задачи, кластеры Кинематика вращательного движения твердого тела. П ( 15 шт)
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
Сингл S014 П Кинематика вращательного движения твердого тела. Аналитические задачи, П (s014, 15 шт)1. [Уд1] (О) Вектор, равный по модулю углу поворота твердого тела и направленный вдоль оси вращения, называется … перемещением тела. :угловым 2. [Уд1] (О) Направление вектора углового перемещения тела связано с направлением вращения тела правилом … буравчика. :правого 3. [Уд1] (ВО1) При вращательном движении тела вокруг оси из векторов, являющихся кинематическими характеристиками движения, при любом характере вращения сонаправленными будут вектора 1) 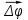 , , 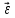 2) 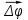 , , 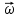 3) 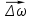 , , 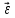 4) все вектора направлены одинаково при любом движении :2 4. [Уд3] (ВОМ) При вращательном движении тела вокруг оси из векторов, являющихся кинематическими характеристиками движения, при вращении могут быть направлены в противоположные стороны вектора следующих пар: 1) 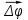 , , 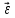 2) 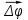 , , 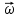 3) 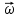 , , 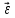 :1,3 5. [Уд1] (ВО1) Вектор угловой скорости материальной точки определяется формулой 1) 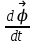 2) 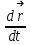 3) 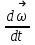 4) 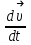 :1 6. [Уд1] (ВО1) Вектор углового ускорения материальной точки определяется формулой 1) 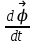 2) 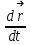 3) 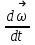 4) 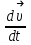 :3 7. [Уд1] (О) Частица движется вдоль окружности радиусом R= 1м в соответствии с уравнением 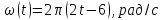 . Время движения до остановки равно … сек. . Время движения до остановки равно … сек.:3 8. [Уд1] (ВО1) Проекция угловой скорости тела на ось вращения зависит от времени согласно уравнению 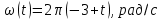 . Проекция углового ускорения при этом движении равна . Проекция углового ускорения при этом движении равна 1) 2π 2) –2π 3) 6π 4) – 6π :1 9. [Уд1] (ВО1) Частица движется вдоль окружности радиусом R = 1м в соответствии с уравнением  , где φ – в радианах, t–в секундах. Проекция угловой скорости через 2 с после начала движения равна , где φ – в радианах, t–в секундах. Проекция угловой скорости через 2 с после начала движения равна 1) 2π 2) –2π 3) 4π 4) -4π :4 1 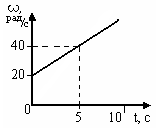 0. [Уд1] (ВО1) На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Уравнение, верно отражающее зависимость угловой скорости от времени, имеет вид 0. [Уд1] (ВО1) На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Уравнение, верно отражающее зависимость угловой скорости от времени, имеет вид 1) 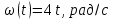 2) 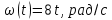 3) 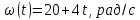 4) 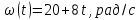 :3 1 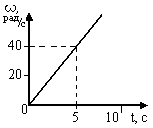 1. [Уд1] (ВО1) На графике представлена зависимость угловой скорости тела, вращающегося вокруг неподвижной оси, по окружности, от времени t. 1. [Уд1] (ВО1) На графике представлена зависимость угловой скорости тела, вращающегося вокруг неподвижной оси, по окружности, от времени t. Уравнение, верно отражающее представленную зависимость, имеет вид 1) 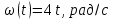 2) 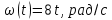 3) 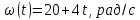 4) 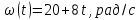 :2 1 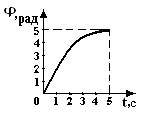 2.[Уд3] (ВОМ) На графике представлена зависимость угла поворота φ тела, вращающегося вокруг неподвижной оси, от времени t. Про характер движения рассматриваемого тела можно утверждать, что оно вращается 2.[Уд3] (ВОМ) На графике представлена зависимость угла поворота φ тела, вращающегося вокруг неподвижной оси, от времени t. Про характер движения рассматриваемого тела можно утверждать, что оно вращается 1) равноускоренно с начальной скоростью равной нулю 2) равноускоренно с отличной от нуля начальной скоростью 3) равнозамедленно с конечной скоростью равной нулю 4) равнозамедленно с отличной от нуля начальной скоростью :3,4 1 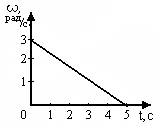 3. [Уд1] (О) На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. До остановки тело повернется на угол, равный … рад. (с округлением до десятых долей). 3. [Уд1] (О) На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. До остановки тело повернется на угол, равный … рад. (с округлением до десятых долей).:7,5 1  4. [Уд1] (О) На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Модуль углового ускорения равен … рад/с (с округлением до десятых долей). 4. [Уд1] (О) На графике представлена зависимость угловой скорости ω(t) тела, вращающегося вокруг неподвижной оси, от времени t. Модуль углового ускорения равен … рад/с (с округлением до десятых долей).:0,6 1 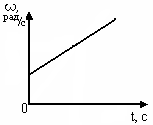 5. [Уд1] (ВО1) Угловая скорость точки, движущейся по окружности, изменяется с течением времени так, как показано на графике. Угол между векторами ускорения 5. [Уд1] (ВО1) Угловая скорость точки, движущейся по окружности, изменяется с течением времени так, как показано на графике. Угол между векторами ускорения 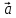 и мгновенной скорости и мгновенной скорости 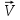 с течением времени с течением времени1) увеличивается 2) уменьшается 3) не изменяется :1 V 041 Динамика вращательного движения. Момент силы. Момент импульса. Момент инерции тел. кластер П( c041, 7 шт) 1. [Уд3] (ВОМ) Момент инерции однородного тела зависит от: 1) момента приложенных к телу сил при заданной оси вращения 2) выбора оси вращения 3) формы тела 4) массы тела 5) углового ускорения :2,3,4 2. [Уд1] (ВО1) И 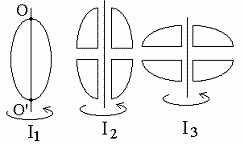 з жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси ОО. Для моментов инерции относительно оси ОО справедливо соотношение з жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси ОО. Для моментов инерции относительно оси ОО справедливо соотношение 1) I1< I2 < I3 2) I1= I2 = I3 3) I1< I2 = I3 4)I1> I2 > I3 :1 3 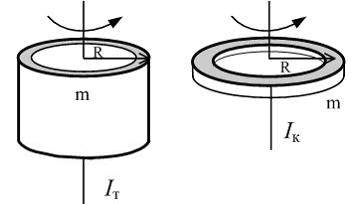 . [Уд1] (ВО1) Тонкостенная трубка и кольцо имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение . [Уд1] (ВО1) Тонкостенная трубка и кольцо имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение1) Iк = IТ 2) Iк > IТ 3) Iк < IТ :1 4 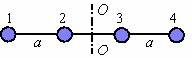 . [Уд1] (ВО1) Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы. Массы шариков слева направо: 1 г, 2 г, 3 г, 4 г. Если поменять местами шарики 2 и 3, то то момент инерции этой системы относительно оси О, перпендикулярной прямой а и проходящей через середину системы . [Уд1] (ВО1) Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы. Массы шариков слева направо: 1 г, 2 г, 3 г, 4 г. Если поменять местами шарики 2 и 3, то то момент инерции этой системы относительно оси О, перпендикулярной прямой а и проходящей через середину системы 1) увеличится 2) не изменится 3) уменьшится :2 5. [Уд1] (ВО1) Момент импульса 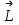 твердого тела относительно оси вращения рассчитывается по формуле твердого тела относительно оси вращения рассчитывается по формуле 1) 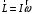 2) 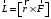 3) 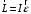 4) 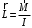 :1 6. [Уд1 (ВО1) Направление момента силы, вызывающего вращение тела, совпадает с направлением вектора 1) силы 2) изменения момента импульса 3) момента импульса тела в начальный момент времени 4) момента импульса тела в конечный момент времени :2 7. [Уд1] (ВО1) Направление изменения момента импульса вращающегося тела всегда совпадает с направлением вектора 1) момента силы 2) угловой скорости 3) момента импульса тела в начальный момент времени 4) момента импульса тела в конечный момент времени :1 синглы П(s041, 15 шт) 1 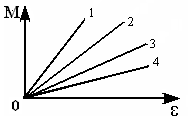 . [Уд1] (О) На рисунке приведена зависимость модуля моментов приложенных к телу сил от модуля углового ускорения тел. Наибольший момент инерции имеет тело под номером … . [Уд1] (О) На рисунке приведена зависимость модуля моментов приложенных к телу сил от модуля углового ускорения тел. Наибольший момент инерции имеет тело под номером …:1 2. [Уд1] (ВО1) Векторная форма основного закона динамики вращательного движения абсолютно твердого тела в импульсном виде – 1) 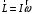 2) 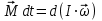 3) 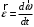 4)  :2 2. [Уд1] (ВО1) Формула, отражающая связь момента сил, действующих на тело, с моментом импульса этого тела – 1) 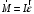 2) 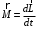 3)  4) 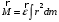 :2 3. [Уд1] (ВО1) На рисунке приведен график зависимости модуля результирующего момента сил, действующих на вращающееся твердое тело, от времени. Тело вращалось равномерно на интервале времени 1) от 0 до t1 2) от t1 до t2 3 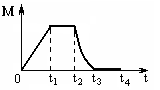 ) от t2 до t3 ) от t2 до t34) от t3 до t4 :4 4  . [Уд1] (ВО1) На рисунке приведен график зависимости модуля результирующего момента сил, действующих на вращающееся твердое тело, от времени. Тело вращалось с постоянным угловым ускорением на интервале времени . [Уд1] (ВО1) На рисунке приведен график зависимости модуля результирующего момента сил, действующих на вращающееся твердое тело, от времени. Тело вращалось с постоянным угловым ускорением на интервале времени 1) от 0 до t1 2) от t1 до t2 3) от t2 до t3 4) от t3 до t4 :2 5 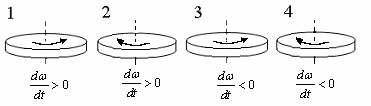 . [Уд3] (ВО) На рисунках стрелками показаны направления вращения дисков и указано, как изменяется угловая скорость со временем. Вращающий момент сил, направленный вниз, приложен к дискам, приведенным под номерами: … . [Уд3] (ВО) На рисунках стрелками показаны направления вращения дисков и указано, как изменяется угловая скорость со временем. Вращающий момент сил, направленный вниз, приложен к дискам, приведенным под номерами: …1) 1 и 2 2) 1 и 3 3) 1 и 4 4) 2 и 3 5) 2 и 4 6) 3 и 4 :4 6 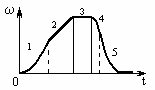 . [Уд1] (О) На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. . [Уд1] (О) На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения.Момент действующих на тело сил был постоянным и не равным нулю на участке … :2 7  . [Уд1] (О) На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. . [Уд1] (О) На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения.Момент импульса тела убывал на участках: … :4,5 8. [Уд1] (О) На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Максимальное по модулю угловое ускорение соответствует участку … :  4 49. [Уд1] (ВО1) Четыре шарика, размеры которых пренебрежимо малы, движутся по окружностям с одинаковой угловой скоростью. Массы шариков  и радиусы окружностей и радиусы окружностей  указаны на рисунках. Момент импульса относительно оси, проходящей через центр окружности, максимален у шарика … указаны на рисунках. Момент импульса относительно оси, проходящей через центр окружности, максимален у шарика … 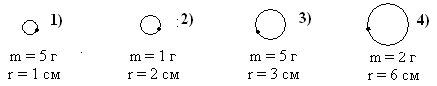 :4 10. [Уд1] (ВО1) На тело действует постоянный вращающий момент. Из ниже перечисленных характеристик вращательного движения в этом случае изменяется с течением времени пропорциональна квадрату времени следующая величина – 1) угол поворота 2) угловая скорость 3) угловое ускорение 4) момент импульса :1 11. [Уд1] (ВО1) На тело действует постоянный вращающий момент. Из перечисленных ниже величин изменяется со временем по линейному закону величина – 1) момент инерции 2) угловое ускорение 3) угловая скорость 4) кинетическая энергия вращения :3 12. [Уд1] (ВО1) Основное уравнение динамики вращательного движения – 1) 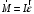 2) 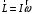 3) 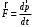 4)  :1 13. [Уд1] (ВО1) Формула, выражающая второй закон Ньютона для вращательного движения – 1) 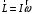 2)  3) 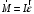 4) 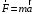 :3 1 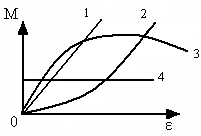 4. [Уд1] (О) На рисунке приведены различные виды графиков. Основному закону вращательного движения соответствует график…. 4. [Уд1] (О) На рисунке приведены различные виды графиков. Основному закону вращательного движения соответствует график….:1 15. [Уд1] (О) Верно указано направление момента силы для тела, совершающего равнозамедленное вращение, на рисунке … 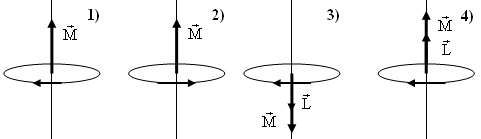 :1 Дисциплина: Физика Тема: 110 Физические основы молекулярной физики V114 – П Распределения Максвелла и Больцмана S114 – П Распределение Больцмана (3 задания) 1. Н 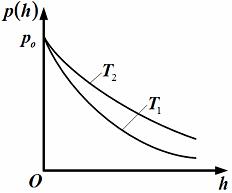 а рисунке представлены зависимости давления от высоты для изотермической атмосферы, которые описываются барометрической формулой а рисунке представлены зависимости давления от высоты для изотермической атмосферы, которые описываются барометрической формулой 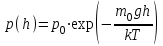 . Температуры связаны между собой соотношением . Температуры связаны между собой соотношением 1) T1 = T2 2) T1 > T2 3) T1 < T2 :3 2. Воздух у поверхности Земли находится при нормальных условиях (100 кПа и 00 С) и его температура и ускорение свободного падения g = 9,8 м/с2 не зависит от высоты. Молярная масса равна M = 2910-3 кг/моль. Тогда отношение давления P1 воздуха на высоте 1 км к давлению P2 на дне скважины глубиной 1 км составляет 1) 0,5 2) 0,8 3) 1,2 4) 1,5 :2 3. Если температуру воздуха и ускорение силы тяжести считать не зависящими от высоты(t = 100 С, g = 9,8 м/с2, и M = 2910-3 кг/моль), то плотность воздуха в e раз (e - основание натурального логарифма) меньше по сравнению с его плотностью на уровне моря на высоте … км. 1) 8,3 2) 6,5 3) 1,2 4) 4,7 :1 C 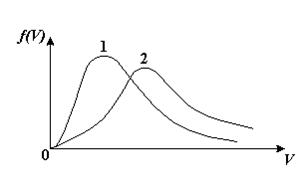 114 – П Распределение Максвелла – 13 заданий 114 – П Распределение Максвелла – 13 заданий1. Для распределения Максвелла по модулям скоростей молекул для разных газов при одинаковой температуре верны утверждения: 1) График 1 соответствует газу с большей массой молекул 2) График 2 соответствует газу с большей молярной массой. 3) Площадь под этими кривыми тем больше, чем больше молярная масса газа 4) Площади под этими кривыми одинаковы. :1,4 2. Верные утверждения: 1) функция распределения Максвелла f(v) зависит от массы молекулы газа 2) функция распределения Максвелла f(v) не зависит от температуры 3) f(v) является величиной размерной 4) f(v) носит экстремальный характер :1,3,4 3. При изменении температуры Т газа средняя квадратичная скорость молекул этого газа увеличилась в 3 раза. Тогда максимальное значение функции распределения Максвелла 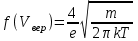 (e - основание натурального логарифма, VB - наиболее вероятная скорость молекул) … раз(а). (e - основание натурального логарифма, VB - наиболее вероятная скорость молекул) … раз(а).1) увеличится в 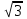 2) уменьшится в 9 3) уменьшится в 3 4) увеличится в 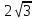 : 3 4. Правильные утверждения о средней квадратичной скорости ( 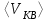 ) частиц системы, подчиняющейся распределению Максвелла: ) частиц системы, подчиняющейся распределению Максвелла:1) При одинаковой температуре 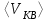 молекул различных идеальных газов одинакова. молекул различных идеальных газов одинакова.2) Средняя квадратичная скорость 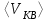 молекул газа при любой температуре меньше наиболее вероятной скорости. молекул газа при любой температуре меньше наиболее вероятной скорости.3) Чем больше масса молекулы газа, тем меньше 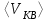 . .4) При возрастании температуры системы в четыре раза средняя квадратичная скорость 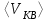 молекул увеличивается в два раза. молекул увеличивается в два раза.:3,4 5. Если средняя квадратичная скорость молекул водорода (M = 210-3 кг/моль) больше наиболее вероятной на V= 400 м/с, то температура газа равна … К. 1) 180 2) 381 3) 230 4) 450 :2 6. Если средняя квадратичная скорость молекул некоторого газа равна 500 м/с, то наиболее вероятная скорость составляет … м/с. 1) 327 2) 250 3) 630 4) 408 :4 7. Если при нагревании некоторого газа наиболее вероятная скорость молекул газа увеличилась в 2 раза, то средняя квадратичная скорость … раз(а). 1) увеличится в 4 2) уменьшится в 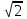 3) уменьшится в 8 4) увеличится в 2 :4 8. Если при нагревании некоторого газа средняя квадратичная скорость молекул газа увеличилась в 4 раза, при этом наиболее вероятная скорость … раз(а). 1) увеличится в 4 2) уменьшится в 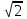 3) уменьшится в 8 4) увеличится в 2 :1 9. Три газа: водород, гелий и кислород находятся при одинаковой температуре T. Тогда значение f(Vвер) функции распределения Максвелла, соответствующее наиболее вероятной скорости молекул,.. 1)одинаково для всех газов 2) максимально для водорода 3) минимально для гелия 4) максимально для кислорода :4 10. Три газа: водород, гелий и кислород находятся при одинаковой температуре T. Тогда наиболее вероятная скорость Vвер… 1) у всех газов одинакова 2) у кислорода наибольшая 3) у гелия наименьшая 4) у водорода наибольшая : 4 11В статистике Максвелла функция распределения имеет вид 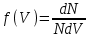 . НЕВЕРНОЕ утверждение о функции Максвелла – . НЕВЕРНОЕ утверждение о функции Максвелла – 1) f(V) - вероятность того, что скорость данной молекулы находится в единичном интервале скоростей вблизи заданной скорости V. 2) f(V)dV- вероятность того, что скорость данной молекулы заключена в интервале скоростей от V до V+dV. 3) f(V) - относительное число молекул, скорости которых заключены в интервале скоростей от V до V+dV. 4) f(V)NdV - абсолютное число молекул, скорости которых заключены в интервале скоростей от V до V+dV. :4 12Правильные утверждения о наиболее вероятной скорости Vвер частиц системы, подчиняющейся распределению Максвелла: 1) Наиболее вероятная скорость Vвер зависит от температуры и молярной массы идеального газа. 2) Скорость Vвер можно найти, приравняв нулю производную функции распределения Максвелла по скоростям: 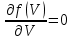 . .3) Чем больше молярная масса газа, тем меньше при данной температуре значение Vвер. 4) Vвер линейно возрастает с увеличением температуры. :1,2,3 13. . Н 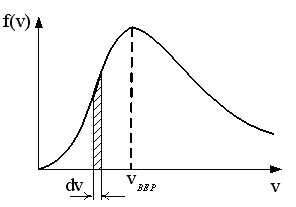 а рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где а рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 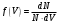 - доля молекул, скорости которых заключены в интервале от - доля молекул, скорости которых заключены в интервале от 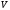 до до 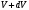 в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большеймолярной массой и таким же числом молекул, то в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большеймолярной массой и таким же числом молекул, то1) величина максимума уменьшится 2) площадь под кривой увеличится 3) максимум кривой сместится влево, в сторону меньших скоростей 4) максимум кривой сместится вправо, в сторону больших скоростей :3 ема: 121 Первое начало термодинамики V121П Первое начало термодинамики. S121 П Первое начало термодинамики (23 задания) 1. Для адиабатического процесса в идеальном газе справедливы утверждения: 1) В ходе процесса газ не обменивается энергией с окружающими его телами (ни в форме работы, ни в форме теплопередачи). 2) Если газ расширяется, то его внутренняя энергия уменьшается. 3) Если газ расширяется, то его внутренняя энергия увеличивается. 4) В ходе процесса изменяются параметры состояния газа – объем, давление, температура. : 2, 4 2 Правильные утверждения о внутренней энергии системы: 1) внутренняя энергия системы является функцией ее состояния – зависит от ее термодинамических параметров состояния 2) во внутреннюю энергию системы не входит механическая энергия движения и взаимодействия системы как целого 3) приращение внутренней энергии зависит от пути (способа) перехода системы из начального состояния в конечное 4) внутренние энергии двух тел, находящихся в тепловом равновесии друг с другом, всегда одинаковы : 1, 2 3. ). Двухатомному идеальному газу в результате изобарического процесса подведено количество теплоты 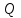 . На увеличение внутренней энергии газа расходуется часть теплоты . На увеличение внутренней энергии газа расходуется часть теплоты 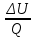 , равная , равная 1) 0,29 2) 0,71 3) 0,60 4) 0,25 :2 4. [Уд] (ВО1) Формулировками первого начала термодинамики могут служить утверждения: 1) В адиабатически замкнутой системе энтропия при любых процессах не может убывать. 2) Количество тепла, подведенное к системе, затрачивается на изменение ее внутренней энергии и на совершение системой работы против внешних сил. 3) При любом круговом процессе система может совершить работу, большую, чем подведенное к ней количество теплоты. 4)  , где S– энтропия системы, k–постоянная Больцмана, аW– термодинамическая вероятность. , где S– энтропия системы, k–постоянная Больцмана, аW– термодинамическая вероятность.: 2 5. [Уд1] (ВО1) В результате изобарического нагревания одного моля идеального двухатомного газа, имеющего начальную температуру  , его объем увеличился в 2 раза. Для этого к газу надо подвести количество теплоты, равное , его объем увеличился в 2 раза. Для этого к газу надо подвести количество теплоты, равное1) 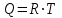 2) 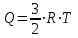 3) 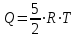 4) 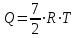 :4 6. [Уд1] (ВО1) Двум молям водорода сообщили 580 Дж теплоты при постоянном давлении. При этом его температура повысилась на … К. 1) 10 2) 27 3) 38 4) 45 :1 7. [Уд1] (ВО1) У водорода, взятом в количестве 2 моль при постоянном давлении, температура повысилась на 10 К. При этом ему сообщили количество теплоты, равное … Дж. 1) 370 2) 580 3) 640 4) 925 :2 8. [Уд1] (ВО1) Водороду, имеющему постоянный объем, сообщили 580 Дж теплоты и его температура повысилась на 10 К. Количество вещества составляет … моль. 1) 2,8 2) 3,5 3) 4,7 4) 6,8 :1 9. [Уд] (ВО1). Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты 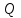 . На работу газа расходуется часть теплоты . На работу газа расходуется часть теплоты 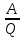 , равная , равная 1) 0,40 2) 0,75 3) 0,60 4) 0,25 :1 10. [Уд] (ВО1). Двухатомному идеальному газу в результате изобарического процесса подведено количество теплоты 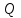 . На работу газа расходуется часть теплоты . На работу газа расходуется часть теплоты 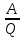 , равная , равная1) 0,41 2) 0,73 3) 0,56 4) 0,29 :4 11. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изобарического и кругового процессов в идеальных газах, приведены под номерами: 1) Q= U+ A 2) 0 = U + A 3) Q = U 4) Q = A :1, 4 12. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изохорического и изотермического процессов в идеальных газах, приведены под номерами: 1) Q= U+ A 2) 0 = U + A 3) Q = U 4) Q = A :3, 4 13. [Уд1] (ВОМ) Уравнения, выражающие первое начало термодинамики для изохорического и изобарического процессов в идеальных газах, приведены под номерами: 1) Q= U+ A 2) 0 = U + A 3) Q = U 4) Q = A :1, 3 14. [Уд1] (ВО1) Работа, совершаемая в изотермическом процессе, определяется формулой 1) 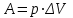 2) 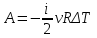 3) 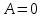 4) 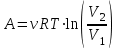 :4 15. [Уд1] (ВО1) Работа, совершаемая газом в изохорическом процессе, определяется формулой под номером 1) 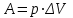 2) 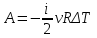 3) 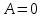 4) 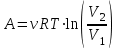 :3 16. [Уд1] (ВО) Внутренняя энергия идеального двухатомного газа выражается формулой 1) 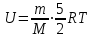 2) 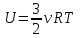 3)  4) 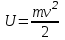 : 1 17. [Уд] (ВО1). Одноатомному идеальному газу в результате изобарического процесса подведено количество теплоты 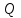 . На увеличение внутренней энергии газа расходуется часть теплоты . На увеличение внутренней энергии газа расходуется часть теплоты 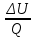 , равная , равная 1) 0,40 2) 0,75 3) 0,60 4) 0,25 :3 18. [Уд1] (ВО1) При изобарическом процессе в идеальном газе его объем возрос в два раза. Внутренняя энергия газа при этом 1) увеличилась в два раза 2) уменьшилась в два раза 3) не изменилась 4) увеличилась в 4 раза :1 19. [Уд1] (ВО1) Один моль одноатомного идеального газа, имеющий начальную температуру T = 250 К, нагрели изобарически. При этом его объем увеличился в 2 раза. Изменение внутренней энергии 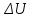 газа равно … кДж. газа равно … кДж.1) 2,7 2) 3,1 3) 3,8 4) 4,5 : 2 20. [Уд] (ВО1). Многоатомному идеальному газу в результате изобарического процесса подведено количество теплоты 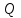 . На увеличение внутренней энергии газа расходуется часть теплоты . На увеличение внутренней энергии газа расходуется часть теплоты 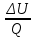 , равная , равная 1) 0,40 2) 0,75 3) 0,60 4) 0,25 :2 21. [Уд1] (ВО1) Внутренняя энергия идеального многоатомного газа выражается формулой 1) 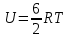 2) 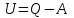 3) 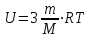 4) 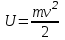 : 3 22. [Уд1] (ВО1) В результате изобарического нагревания одного моля идеального одноатомного газа, взятого при температуре T, его объем увеличился в 2 раза. Для этого к газу надо подвести количество теплоты, равное 1) 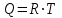 2) 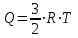 3) 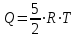 4) 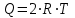 :3 23. [Уд1] (ВО1) При адиабатическом расширении ν= 2 моль одноатомного идеального газа совершена работа, равная 2493 Дж. При этом изменение температуры составило … К. 1) 100 2) 200 3) 300 4) 400 :1 С121 П Первое начало термодинамики ( Работа с графиками ) 12 заданий 1 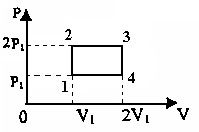 . [Уд1] (ВО) Одноатомный идеальный газ совершает круговой процесс, состоящий из двух изохор и двух изобар (см. рисунок). Отношение работы . [Уд1] (ВО) Одноатомный идеальный газ совершает круговой процесс, состоящий из двух изохор и двух изобар (см. рисунок). Отношение работы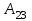 , совершенной газом на участке 2–3, к количеству теплоты , совершенной газом на участке 2–3, к количеству теплоты 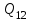 , полученного газом на участке 1–2, , полученного газом на участке 1–2, 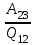 равно равно1) 0,5 2) 1 3) 1,33 4) 2,5 :3 2 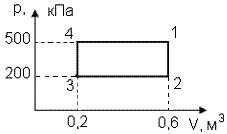 . [Уд] (ВО1) Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании газа к работе при охлаждении равно . [Уд] (ВО1) Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке. Отношение работы при нагревании газа к работе при охлаждении равно1) 5 2) 3 3) 1,5 4) 2,5 : 4. 3 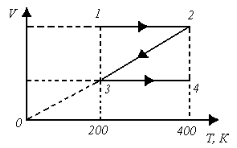 . [Уд1] (ВО1) Двухатомный идеальный газ, взятый в количестве 3,0 моль, совершает процесс, изображенный на рисунке. Изменение внутренней энергии U1-4 в ходе всего процесса, равно … кДж. . [Уд1] (ВО1) Двухатомный идеальный газ, взятый в количестве 3,0 моль, совершает процесс, изображенный на рисунке. Изменение внутренней энергии U1-4 в ходе всего процесса, равно … кДж.1) 7,5 2) 9,0 3) 12,5 4) 14,6 :3 4 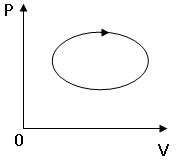 . [Уд] (ВОМ) Термодинамическая система совершила круговой процесс, изображенный на рисунке. При этом: . [Уд] (ВОМ) Термодинамическая система совершила круговой процесс, изображенный на рисунке. При этом:1) система обменивалась с окружающими телами теплом 2) внутренняя энергия системы изменилась по завершении этого кругового процесса 3) работа, совершаемая системой в этом круговом процессе равна нулю 4) работа, совершаемая системой в этом круговом процессе, отлична от нуля :1, 4 5 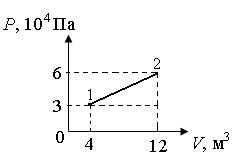 . [Уд1] (ВО1) При переходе из состояния1 в состояние 2 у двухатомного газа внутренняя энергия изменяется на … МДж. . [Уд1] (ВО1) При переходе из состояния1 в состояние 2 у двухатомного газа внутренняя энергия изменяется на … МДж.1) 0,70 2) 1,50 3) 2,80 4) 3,40 :2 6. [Уд1] (ВО1) Гелий совершает круговой процесс, состоящий из двух изохор и двух изобар (см. рисунок). Изменение внутренней энергии  газа на участке 1–2 равно газа на участке 1–2 равно1  ) 0,5 P1V1 ) 0,5 P1V12) 1,5 P1V1 3) 2 P1V1 4) 4 P1V1 :2 7  . [Уд1] (ВО1) Азот совершает круговой процесс, состоящий из двух изохор и двух изобар (см. рисунок). Количество теплоты, полученное газом . [Уд1] (ВО1) Азот совершает круговой процесс, состоящий из двух изохор и двух изобар (см. рисунок). Количество теплоты, полученное газом  от нагревателя от нагревателя1) 4 P1V1 2) 6,5 P1V1 3) 9,5 P1V1 4) 12 P1V1 :3 8 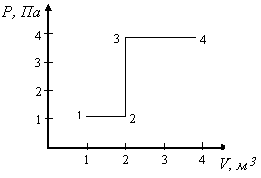 . [Уд1] (ВО1) При переходе из состояния 1 в состояние 4 внутренняя энергия двухатомного идеального газа … Дж. . [Уд1] (ВО1) При переходе из состояния 1 в состояние 4 внутренняя энергия двухатомного идеального газа … Дж.1) увеличилась на 22,5 Дж. 2) уменьшилась на 22,5 Дж. 3) увеличилась на 37,5 Дж. 4) уменьшилась на 37,5 Дж. :3 9. [Уд1] (ВО1) При переходе из состояния 1 в состояние 4 отношение количества теплоты 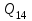  , полученного двухатомным газом к работе , полученного двухатомным газом к работе 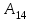 , совершенной газом в этом процессе, , совершенной газом в этом процессе, 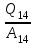 равно равно1) 1,5 2) 2,7 3) 4,6 4) 5,2 :4 1  0. [Уд1] (ВО1) Одноатомный идеальный газ, взятый в количестве 2,0 моль, совершает процесс 1 – 2 – 3 – 4, изображенный на рисунке. Работа 0. [Уд1] (ВО1) Одноатомный идеальный газ, взятый в количестве 2,0 моль, совершает процесс 1 – 2 – 3 – 4, изображенный на рисунке. Работа 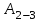 , совершаемая газом в процессе 2–3, равна … кДж. , совершаемая газом в процессе 2–3, равна … кДж.1) -1,4 2) -2,8 3) - 3,3 4) - 6,6 :3 1  1. [Уд1] (ВО1) Одноатомный идеальный газ, взятый в количестве 2,0 моль, совершает процесс 1 – 2 – 3 – 4, изображенный на рисунке. Количество теплоты, отданное газом 1. [Уд1] (ВО1) Одноатомный идеальный газ, взятый в количестве 2,0 моль, совершает процесс 1 – 2 – 3 – 4, изображенный на рисунке. Количество теплоты, отданное газом 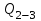 в процессе 2–3, равно … кДж. в процессе 2–3, равно … кДж.1) 5,1 2) 4,8 3) 8,3 4) 7,6 :3 1  2. [Уд1] (ВО1) При переходе из состояния 1 в состояние 4 внутренняя энергия двухатомного идеального газа изменилась на …….. Дж 2. [Уд1] (ВО1) При переходе из состояния 1 в состояние 4 внутренняя энергия двухатомного идеального газа изменилась на …….. Дж1) 22,5 2) 76,2 3) 58,1 4) 37,5 :4 – П Энтропия и второе начало термодинамики. S124 –П Энтропия и второе начало термодинамики (10 заданий) . 1 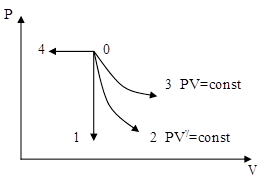 . [Уд1] (ВОМ). Система может перейти из состояния 0 в состояния 1,2,3,4 (см. рисунок). Энтропия системы уменьшается в процессах: . [Уд1] (ВОМ). Система может перейти из состояния 0 в состояния 1,2,3,4 (см. рисунок). Энтропия системы уменьшается в процессах:1) 0 1 2) 0 2 3) 0 3 4) 0 4 :1, 4 2 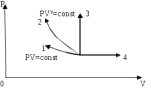 . [Уд1] (ВОМ). Система может перейти из состояния 0 в состояния 1,2,3,4 (см. рисунок). Энтропия системы возрастает в процессах: . [Уд1] (ВОМ). Система может перейти из состояния 0 в состояния 1,2,3,4 (см. рисунок). Энтропия системы возрастает в процессах:1) 0 1 2) 0 2 3) 0 3 4) 0 4 :3, 4 3. [Уд1] (ВОМ). Один моль гелия и один моль азота, находящиеся в закрытых сосудах, нагрели от температуры Т1 до температуры Т2. Тогда 1) изменения энтропий этих газов не зависят от объемов сосудов 2) изменения энтропий этих газов не зависят от скорости нагрева 3) ΔSN2 =ΔSHe 4) ΔSN2 >ΔSHe :2, 4 4. [Уд1] (ВО1). Изотермическое расширение одного моля азота проведено до удвоения объема. Такое же увеличение объема осуществлено для моля гелия. Тогда 1) ΔSN2 >ΔSHe 2) ΔSN2 <ΔSHe 3).Δ SN2 =Δ SHe 4) изменения энтропий этих газов зависят от скорости нагрева :3 5. [Уд1] (ВОМ). Правильные утверждения: 1) равновесие термодинамическое состояние – это такое состояние термодинамической системы, при котором все ее термодинамические параметры остаются постоянными сколь угодно долго. 2) термодинамический процесс – это любое изменение термодинамического состояния системы. 3) неравновесный процесс – процесс, состоящий из ряда следующих друг за другом равновесных состояний. 4) обратимый процесс всегда является равновесным процессом. : 1, 2, 4 6. [Уд1] (ВО1). Воду массой m = 0,1 кг нагревают от 0С до 100С и превращают в пар. Удельная теплоемкость воды cУД = 4,19103 Дж/кгК. Изменение энтропии при нагревании равно … Дж/К. 1) 131 2) 250 3) 347 4) 589 :1 7. [Уд1] (ВО1). При изобарическом расширении массы m = 8 г гелия от объема V1 = 10 л до объема V2 = 25 л приращение S энтропии равно … Дж/К. 1) 14,9 2) 38,1 3) 37,6 4) 43,5 :2 8. [Уд1] (ВО1). При изотермическом расширении массы m = 6 г водорода от давления p1 = 100 кПа до давления p2 = 50 кПа приращение S энтропии равно … Дж/К. 1) 17,3 2) 52,8 3) 87,6 4) 46,5 :1 9. [Уд1] (ВО1). Масса m = 10 г кислорода изохорически нагревается от температуры t1 = 500 C до температуры t2 = 1500 С, приращение S энтропии равно … Дж/К. 1) 1,75 2) 2,45 3) 8,76 4) 4,96 :1 10. [Уд1] (ВО1). Масса m = 10 г кислорода изобарически нагревается от температуры t1 = 500 C до температуры t2 = 1500 С, приращение S энтропии равно… Дж/К. 1) 1,75 2) 2,45 3) 7,63 4) 6,58 :2 C124 –П Тепловые двигатели (4 задания). 1. [Уд1] (ВО1). Н 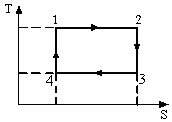 а рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Адиабатное расширение происходит на этапе а рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Адиабатное расширение происходит на этапе 1) 4 – 1 2) 2 – 3 3) 1 – 2 4) 3 - 4 :2. 2. [Уд1] (ВО1). Н  а рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Адиабатное сжатие происходит на этапе а рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Адиабатное сжатие происходит на этапе 1) 4 – 1 2) 2 – 3 3) 1 – 2 4) 3 - 4 :1. 3. [Уд1] (ВО1). Н  а рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Изотермическое расширение происходит на этапе а рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Изотермическое расширение происходит на этапе 1) 4 – 1 2) 2 – 3 3) 1 – 2 4) 3 - 4 :3. 4. [Уд1] (ВО1). Н  а рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Изотермическое сжатие происходит на этапе а рисунке изображен цикл Карно в координатах (Т,S), где S – энтропия. Изотермическое сжатие происходит на этапе 1) 4 – 1 2) 2 – 3 3) 1 – 2 4) 3 - 4 :4. |
