егэ5. Кодирование и декодирование информации
 Скачать 420 Kb. Скачать 420 Kb.
|
|
© К. Поляков, 2009-2018 5 (базовый уровень, время – 2 мин)Тема: Кодирование и декодирование информации. Что нужно знать: кодирование – это перевод информации с одного языка на другой (запись в другой системе символов, в другом алфавите) обычно кодированием называют перевод информации с «человеческого» языка на формальный, например, в двоичный код, а декодированием – обратный переход один символ исходного сообщения может заменяться одним символом нового кода или несколькими символами, а может быть и наоборот – несколько символов исходного сообщения заменяются одним символом в новом коде (китайские иероглифы обозначают целые слова и понятия) кодирование может быть равномерное и неравномерное; при равномерном кодировании все символы кодируются кодами равной длины; при неравномерном кодировании разные символы могут кодироваться кодами разной длины, это затрудняет декодирование закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова; закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова; условие Фано – это достаточное, но не необходимое условие однозначного декодирования. Пример заданияР-16. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.. Решение: Построим дерево для заданного двоичного кода: 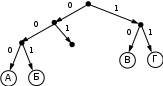 согласно условию Фано, код декодируется однозначно, если все используемые кодовые слова соответствуют листьям такого дерева; видим, что для заданных кодовых слов это условие выполняется может показаться, что ответ – 01, поскольку на эту ветвь можно «подвесить» букву Д, однако это не так – тогда будет некуда подвешивать оставшуюся букву – Е поэтому для того, чтобы добавить в это дерево две буквы (Д и Е) и сохранить выполнение условия Фано, нужно в узле 01 сделать развилку, тогда получается два свободных кода, 010 и 011, из них меньший – 010 Ответ: 010. Ещё пример заданияР-15. По каналу связи с помощью равномерного двоичного кода передаются сообщения, содержащие только 4 буквы: X, Y, Z, W; для кодировки букв используются кодовые слова длины 5. При этом для набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Для кодирования букв X, Y, Z используются 5-битовые кодовые слова: X: 01111, Y: 00001, Z: 11000. Определите 5-битовое кодовое слово для буквы W, если известно, что оно начинается с 1 и заканчивается 0. Решение: По условию кодовое слово для буквы W соответствует маске 1***0, где вместо звёздочек можно поставить 0 или 1. Найдем расстояния Хэмминга – количество позиций, в которых отличается это кодовое слово от известных кодовых слов букв X, Y и Z: X: 01111 Y: 00001 Z: 11000 W: 1***0 W: 1***0 W: 1***0 2+? 2+? 0+? Знаки вопроса обозначают неизвестные неотрицательные числа – количество различающихся позиций в тех битах, которые в кодовом слове для буквы W неизвестны. Как видим, наиболее критичная ситуация сложилась для пары Z-W. Для того, чтобы эти кодовые слова различались в трёх позициях, все неизвестные биты кодового слова буквы W должны иметь значения, обратные соответствующим битам кодового слова для буквы Z, то есть, W = 10110 Проверяем полученное кодовое слово: находим расстояние Хэмминга в парах X-W и Y-W: X: 01111 Y: 00001 Z: 11000 W: 10110 W: 10110 W: 10110 3 4 3 Как видим, для все пар расстояние не меньше трёх, что соответствует условию задачи. Ответ: 10110. Ещё пример заданияР-14. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; для буквы Б – кодовое слово 10. Какова наименьшая возможная сумма длин всех шести кодовых слов? Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений. Решение: это задание удобнее решать с помощью дерева; условие Фано выполняется тогда, когда все выбранные кодовые слова заканчиваются в листьях дерева построим дерево по известным кодовым словам: А – 0, Б – 10: 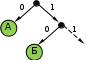 на оставшуюся свободную ветку нужно «повесить» 4 кодовых слова (для букв В, Г, Д, Е) если выбрать один код длиной 3 (В – 110), то оставшиеся 3 кода нужно «повесить» на одну ветку, так, что на ней нужно делать две развилки: 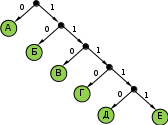 суммарная длина кодовых слов будет в этом случае равна 1 + 2 + 3 + 4 + 2·5 = 20 попробуем другой вариант: оставшиеся 4 кода повесить на 4 ветки одинаковой длины: 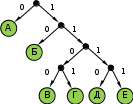 суммарная длина кодовых слов будет в этом случае меньше, чем в предыдущем случае: 1 + 2 + 4·4 = 19 Ответ: 19. Ещё пример заданияР-13. По каналу связи передаются сообщения, каждое из которых содержит 16 букв А, 8 букв Б, 4 буквы В и 4 буквы Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования: а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование); б) общая длина закодированного сообщения должна быть как можно меньше. Какой код из приведённых ниже следует выбрать для кодирования букв А, Б, В и Г? 1) А:0, Б:10, В:110, Г:111 2) А:0, Б:10, В:01, Г:11 3) А:1, Б:01, В:011, Г:001 4) А:00, Б:01, В:10, Г:11 Решение: сначала выберем коды, в которых ни одно кодовое слово не совпадет с началом другого (такие коды называю префиксными) для кода 2 условие «а» не выполняется, так как кодовое слово буквы В (01) начинается с кодового слова буквы А (0) для кода 3 условие «а» не выполняется, так как кодовое слово буквы В (011) начинается с кодового слова буквы Б (01) для кодов 1 и 4 условие выполняется, их рассматриваем дальше считаем общее количество битов в сообщении для кода 1: 16∙1 + 8·2 + 4∙3 + 4∙3 = 56 битов считаем общее количество битов в сообщении для кода 4: 16∙2 + 8·2 + 4∙2 + 4∙2 = 64 бита код 1 даёт наименьшую длину сообщения, поэтому выбираем его Ответ: 1. Ещё пример заданияР-12. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0, для буквы Б – кодовое слово 110. Какова наименьшая возможная суммарная длина всех четырёх кодовых слов? 1) 7 2) 8 3) 9 4) 10 Решение (способ 1, исключение вариантов): условие Фано означает, что ни одно кодовое слово не совпадает с началом другого кодового слова поскольку уже есть кодовое слово 0, ни одно другое кодовое слово не может начинаться с 0 поскольку есть код 110, запрещены кодовые слова 1, 11; кроме того, ни одно другое кодовое слово не может начинаться с 110 таким образом, нужно выбрать еще два кодовых слова, для которых выполняются эти ограничения есть одно допустимое кодовое слово из двух символов: 10 если выбрать кодовое слово 10 для буквы В, то остаётся одно допустимое трёхсимвольное кодовое слово – 111, которое можно выбрать для буквы Г таким образом, выбрав кодовые слова А – 0, Б – 110, В – 10, Г – 111, получаем суммарную длину кодовых слов 9 символов если же не выбрать В – 10, то есть три допустимых трёхсимвольных кодовых слова: 100, 101 и 110; при выборе любых двух их них для букв В и Г получаем суммарную длину кодовых слов 10, что больше 9; поэтому выбираем вариант 3 (9 символов) Ответ: 3. Решение (способ 2, построение дерева): условие Фано означает, что ни одно кодовое слово не совпадает с началом другого кодового слова; при этом в дереве кода все кодовые слова должны располагаться в листьях дерева, то есть в узлах, которые не имеют потомков; построим дерево для заданных кодовых слов А – 0 и Б – 110: 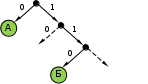 штриховыми линиями отмечены две «пустые» ветви, на которые можно «прикрепить» листья для кодовых слов букв В (10) и Г (111) 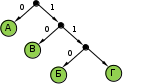 таким образом, выбрав кодовые слова А – 0, Б – 110, В – 10, Г – 111, получаем суммарную длину кодовых слов 9 символов Ответ: 3. Ещё пример заданияР-11. По каналу связи передаются сообщения, содержащие только 5 букв А, И, К, О, Т. Для кодирования букв используется неравномерный двоичный код с такими кодовыми словами: А — 0, И — 00, К — 10, О — 110, Т — 111. Среди приведённых ниже слов укажите такое, код которого можно декодировать только одним способом. Если таких слов несколько, укажите первое по алфавиту. 1) КАА 2) ИКОТА 3) КОТ 4) ни одно из сообщений не подходит Решение: прежде всего заметим, что для заданного кода не выполняется ни прямое, ни обратное условие Фано; «виновата» в этом пара А – И: код буквы А совпадает как с началом, так и с окончанием кода буквы И; больше ни для одной пары кодовых слов прямое условие Фано не нарушено это означает, что не все сообщения могут быть декодированы однозначно теперь нужно понять, какие последовательности могут быть декодированы неоднозначно; в данном случае очевидно, что сообщения АА и И кодируются одинаково: 00, поэтому все слова, где есть АА или И, не могут быть декодированы однозначно поэтому варианты 1 (КАА) и 2 (ИКОТА) отпадают на всякий случай проверим вариант 3: КОТ = 10110111; первой буквой может быть только К (по-другому сочетание 10 получить нельзя), аналогично вторая буква – только О, а третья – только Т Ответ: 3. Ещё пример заданияР-10. По каналу связи передаются сообщения, содержащие только 4 буквы П, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100. Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Решение (способ 1, исключение вариантов): код однозначно декодируется, если выполняется условие Фано или обратное условие Фано; в данном случае «прямое» условие Фано выполняется: с кода буквы О (0) не начинается ни один из двух других кодов; новый код не может начинаться с нуля (иначе нарушится условие Фано) начнём проверку с кодов длиной 1; единственный код, не начинающийся с нуля – 1 – не подходит, потому что с 1 начинаются два других кода: Т (111) и П (100 кодов длиной 2, начинающихся с 1, всего 2: 10 и 11, но их использовать нельзя, потому что с 10 начинается код буквы П, а с 11 – код буквы Т рассматриваем коды длиной 3, начинающиеся с 1; коды 100 и 111 уже заняты, а ещё два – 101 и 110 – свободны и их можно использовать, причём условие Фано выполняется в обоих случаях; поскольку нужно выбрать код с минимальным значением, выбираем 101 Ответ: 101. Решение (способ 2, построение дерева): условие Фано означает, что ни одно кодовое слово не совпадает с началом другого кодового слова; при этом в дереве кода все кодовые слова должны располагаться в листьях дерева, то есть в узлах, которые не имеют потомков; построим дерево для заданных кодовых слов О – 0, Т – 111 и П – 100: 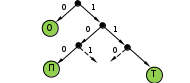 штриховыми линиями отмечены две «пустые» ветви, на которые можно «прикрепить» лист для кодового слова буквы С: 101 или 110; из них минимальное значение имеет код 101 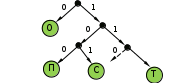 таким образом, выбрав кодовые слова А – 0, Б – 110, В – 10, Г – 111, получаем суммарную длину кодовых слов 9 символов Ответ: 101. Ещё пример заданияР-09. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать? 1) для буквы В – 101 2) это невозможно 3) для буквы В – 010 4) для буквы Б – 10 Решение: код однозначно декодируется, если выполняется условие Фано или обратное условие Фано; в данном случае «прямое» условие Фано выполняется: с кода буквы А (0) не начинается ни один другой код, оставшиеся короткие коды (Б, Г и Д) не совпадают с началом длинного кода буквы В; таким образом, при сокращении нужно сохранить выполнение условия Фано вариант 3 не подходит, потому что новый код буквы В начинается с 0 (кода А), поэтому условие Фано нарушено вариант 4 не подходит, потому что код буквы В начинается с 10 (нового кода б), поэтому условие Фано нарушено вариант 1 подходит, условие Фано сохраняется (все трёхбитные коды различны, ни один не начинается с 0) Ответ: 1. Ещё пример заданияР-08. По каналу связи передаются сообщения, содержащие только 4 буквы: А, И, С, Т. В любом сообщении больше всего букв А, следующая по частоте буква – С, затем – И. Буква Т встречается реже, чем любая другая. Для передачи сообщений нужно использовать неравномерный двоичный код, допускающий однозначное декодирование; при этом сообщения должны быть как можно короче. Шифровальщик может использовать один из перечисленных ниже кодов. Какой код ему следует выбрать? 1) А – 0, И – 1, С – 00, Т – 11 2) С – 1, И – 0, А – 01, Т – 10 3) А – 1, И – 01, С – 001, Т – 000 4) С – 0, И – 11, А – 101, Т – 100 Решение: сначала выберем коды, допускающие однозначное декодирование: это коды 3 и 4 (для них выполняется условие Фано), коды 1 и 2 не подходят для того, чтобы длина сообщения была как можно короче, должно выполнять правило: «чем чаще встречается буква, тем короче её код»; к сожалению, правило, приведённое выше, не совсем «хорошо» выполняется для кодов 3 и 4: в коде 3 длина кодового слова для буквы С больше, чем длина кодового слова буквы И (а хочется наоборот); для кода 4 длина кодового слова для буквы А – не самая маленькая из всех сравним коды 3 и 4, предполагая, что в сообщении буква А встречается раз, буква С – раз, буква И – раз и буква Т – раз; причём по условию задачи > > > при кодировании кодом 3 получаем сообщение длиной L3 = + 3 + 2 +3 при кодировании кодом 4 получаем сообщение длиной L4 = 3 + + 2 +3 находим разность: L4 – L3 = (3 + + 2 +3 ) – ( + 3 + 2 +3 ) = 2 – 2 поскольку > , получаем L4 – L3 > 0, то есть код 3 более экономичный Ответ: 3. Ещё пример заданияР-07. По каналу связи передаются сообщения, содержащие только 4 буквы: Е, Н, О, Т. Для кодирования букв Е, Н, О используются 5-битовые кодовые слова: Е - 00000, Н - 00111, О - 11011. Для этого набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Какое из перечисленных ниже кодовых слов можно использовать для буквы Т, чтобы указанное свойство выполнялось для всех четырёх кодовых слов? 1) 11111 2) 11100 3) 00011 4) не подходит ни одно из указанных выше слов Решение: код, рассмотренный в условии задачи, относится к помехоустойчивым кодам, которые позволяют обнаружить и исправить определенное количество ошибок, вызванных помехами при передаче данных; количество позиций, в которых отличаются два кодовых слова одинаковой длины, называется расстоянием Хэмминга код, в котором расстояние Хэмминга между каждой парой кодовых слов равно d, позволяет обнаружить до d-1 ошибок; для исправления r ошибок требуется выполнение условия d ≥ 2r + 1 поэтому код с d = 3 позволяет обнаружить одну или две ошибки, и исправить одну ошибку. легко проверить, что для заданного кода (Е - 00000, Н - 00111, О - 11011) расстояние Хэмминга равно 3; в таблице выделены отличающиеся биты, их по три в парах Е-Н и Н-О и четыре в паре Е-О: Е – 00000 Е – 00000 Н – 00111 Н – 00111 О – 11011 О – 11011 теперь проверяем расстояние между известными кодами и вариантами ответа; для первого ответа 11111 получаем минимальное расстояние 1 (в паре О-Т), этот вариант не подходит: Е – 00000 Н – 00111 О – 11011 Т - 11111 Т - 11111 Т - 11111 для второго ответа 11100 получаем минимальное расстояние 3 (в парах Е-Т и О-Т): Е – 00000 Н – 00111 О – 11011 Т - 11100 Т - 11100 Т - 11100 для третьего ответа 00011 получаем минимальное расстояние 1 (в паре Н-Т) , этот вариант не подходит: Е – 00000 Н – 00111 О – 11011 Т - 00011 Т - 00011 Т - 00011 таким образом, расстояние Хэмминга, равное 3, сохраняется только для ответа 2 Ответ: 2. Ещё пример задания:Р-06. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа. 1) для буквы Б – 01 2) это невозможно 3) для буквы В – 01 4) для буквы Г – 01 Решение (1 способ, проверка условий Фано): для однозначного декодирования достаточно, чтобы выполнялось условие Фано или обратное условие Фано; проверяем последовательно варианты 1, 3 и 4; если ни один из них не подойдет, придется выбрать вариант 2 («это невозможно»); проверяем вариант 1: А–00, Б–01, В–011, Г–101, Д–111. «прямое» условие Фано не выполняется (код буквы Б совпадает с началом кода буквы В); «обратное» условие Фано не выполняется (код буквы Б совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит; проверяем вариант 3: А–00, Б–010, В–01, Г–101, Д–111. «прямое» условие Фано не выполняется (код буквы В совпадает с началом кода буквы Б); «обратное» условие Фано не выполняется (код буквы В совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит; проверяем вариант 4: А–00, Б–010, В–011, Г–01, Д–111. «прямое» условие Фано не выполняется (код буквы Г совпадает с началом кодов букв Б и В); но «обратное» условие Фано выполняется (код буквы Г не совпадает с окончанием кодов остальных буквы); поэтому этот вариант подходит; правильный ответ – 4. Решение (2 способ, дерево): построим двоичное дерево, в котором от каждого узла отходит две ветки, соответствующие выбору следующей цифры кода – 0 или 1; разместим на этом дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах, составляющих путь от корня до данной буквы (красным цветом выделен код буквы В – 011):  здесь однозначность декодирования получается за счёт того, что при движении от корня к любой букве в середине пути не встречается других букв (выполняется условие Фано); теперь проверим варианты ответа: предлагается перенести одну из букв, Б, В или Г, в узел с кодом 01, выделенный синим цветом видим, что при переносе любой из этих букв нарушится условие Фано; например, при переносе буквы Б в синий узел она оказывается на пути от корня до В, и т.д.; это значит, что предлагаемые варианты не позволяют выполнить прямое условие Фано хочется уже выбрать вариант 2 («это невозможно»), но у нас есть еще обратное условие Фано, для которого тоже можно построить аналогичное дерево, в котором движение от корня к букве дает её код с конца (красным цветом выделен код буквы В – 011, записанный с конца): 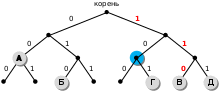 видно, что обратное условие Фано также выполняется, потому что на пути от корня к любой букве нет других букв в заданных вариантах ответа предлагается переместить букву Б, В или Г в синий узел; понятно, что Б или В туда перемещать нельзя – перемещённая буква отказывается на пути от корня к букве Г; а вот букву Г переместить можно, при этом обратное условие Фано сохранится правильный ответ – 4. Ещё пример задания:Р-05. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код: А–1, Б–000, В–001, Г–011. Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. 1) 00 2) 01 3)11 4) 010 Решение: заметим, что для известной части кода выполняется условие Фано – никакое кодовое слово не является началом другого кодового слова если Д = 00, такая кодовая цепочка совпадает с началом Б = 000 и В = 001, невозможно однозначно раскодировать цепочку 000000: это может быть ДДД или ББ; поэтому первый вариант не подходит если Д = 01, такая кодовая цепочка совпадает с началом Г = 011, невозможно однозначно раскодировать цепочку 011: это может быть ДА или Г; поэтому второй вариант тоже не подходит если Д = 11, условие Фано тоже нарушено: кодовое слово А = 1 совпадает с началом кода буквы Д, невозможно однозначно раскодировать цепочку 111: это может быть ДА или ААА; третий вариант не подходит для четвертого варианта, Д = 010, условие Фано не нарушено; правильный ответ – 4.
Еще пример задания:Р-04. Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится 1) 4B16 2) 41116 3)BACD16 4) 102316 Решение: из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный последовательность БАВГ кодируется так: 01 00 10 11 = 1001011 разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем 1001011 = 0100 10112 = 4B16 правильный ответ – 1.
Еще пример задания:Р-03. Решение (вариант 1, декодирование с начала): здесь используется неравномерное кодирование, при котором декодирование может быть неоднозначным, то есть, заданному коду может соответствовать несколько разных исходных сообщений попробуем декодировать с начала цепочки, первой буквой может быть B или E, эти случаи нужно рассматривать отдельно пусть первая буква – E с кодом 011, тогда остается цепочка 0100011000 для кода 0100011000 первой буквой может быть только B с кодом 01, тогда остается 00011000 ( начало исходной цепочки – EB?) для кода 00011000 первой буквой может быть только A с кодом 000, тогда остается 11000, а эта цепочка не может быть разложена на заданные коды букв поэтому наше предположение о том, что первая буква – E, неверно пусть первая буква – B с кодом 01, тогда остается цепочка 10100011000 для кода 10100011000 первой буквой может быть только D с кодом 10, тогда остается 100011000 (можно полагать, что начало исходной цепочки – BD?) для кода 100011000 первой буквой может быть только С с кодом 100, тогда остается 011000 (начало исходной цепочки – BDC?) Несмотря на то, что среди ответов есть единственная цепочка, которая начинается с BDC, здесь нельзя останавливаться, потому что «хвост» цепочки может «не сойтись» для кода 011000 на первом месте может быть B (код 01) или E (011); в первом случае «хвост» 1000 нельзя разбить на заданные коды букв, а во втором – остается код 000 (буква А), поэтому исходная цепочка может быть декодирована как BDCEA правильный ответ – 3
Решение (вариант 2, декодирование с конца): для кода 0110100011000 последней буквой может быть только А (код 000), тогда остается цепочка 0110100011 для 0110100011 последней может быть только буква E (011), тогда остается цепочка 0110100 для 0110100 последней может быть только буква C (100), тогда остается цепочка 0110 для 0110 последней может быть только буква D (10), тогда остается 01 – это код буквы B таким образом, получилась цепочка BDCEA правильный ответ – 3
Решение (вариант 3, кодирование ответов): в данном случае самое простое и надежное – просто закодировать все ответы, используя приведенную таблицу кодов, а затем сравнить результаты с заданной цепочкой получим 1) EBCEA – 01101100011000 2) BDDEA – 011010011000 3) BDCEA – 0110100011000 4) EBAEA – 01101000011000 сравнивая эти цепочки с заданной, находим, что правильный ответ – 3.
Еще пример задания:Р-02. Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=0, Б=10, В=110. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы? 1) 1 2) 1110 3) 111 4) 11 Решение (вариант 1, метод подбора): рассмотрим все варианты в порядке увеличения длины кода буквы Г начнем с Г=1; при этом получается, что сообщение «10» может быть раскодировано двояко: как ГА или Б, поэтому этот вариант не подходит следующий по длине вариант – Г=11; в этом случае сообщение «110» может быть раскодировано как ГА или В, поэтому этот вариант тоже не подходит третий вариант, Г=111, дает однозначное раскодирование во всех сочетаниях букв, поэтому… … правильный ответ – 3.
Решение (вариант 2, «умный» метод): для того, чтобы сообщение, записанное с помощью неравномерного по длине кода, однозначно раскодировалось, требуется, чтобы никакой код не был началом другого (более длинного) кода; это условие называют условием Фано как и в первом решении, рассматриваем варианты, начиная с самого короткого кода для буквы Г; в нашем случае код Г=1 является началом кодов букв Б и В, поэтому условие Фано не выполняется, такой код не подходит код Г=11 также является началом другого кода (кода буквы В), поэтому это тоже ошибочный вариант третий вариант кода, Г=111, не является началом никакого уже известного кода; кроме того, ни один уже имеющийся код не является началом кода 111; таким образом, условие Фано выполняется поэтому правильный ответ – 3.
Еще пример задания1:Р-01. Черно-белое растровое изображение кодируется построчно, начиная с левого верхнего угла и заканчивая в правом нижнем углу. При кодировании 1 обозначает черный цвет, а 0 – белый. Для компактности результат записали в шестнадцатеричной системе счисления. Выберите правильную запись кода. 1) BD9AA5 2) BDA9B5 3) BDA9D5 4) DB9DAB Решение: «вытянем» растровое изображение в цепочку: сначала первая (верхняя) строка, потом – вторая, и т.д.:
в этой полоске 24 ячейки, черные заполним единицами, а белые – нулями:
поскольку каждая цифра в шестнадцатеричной системе раскладывается ровно в 4 двоичных цифры, разобьем полоску на тетрады – группы из четырех ячеек (в данном случае все равно, откуда начинать разбивку, поскольку в полоске целое число тетрад – 6):
переводя тетрады в шестнадцатеричную систему, получаем последовательно цифры B (11), D(13), A(10), 9, D(13) и 5, то есть, цепочку BDA9D5 поэтому правильный ответ – 3.
Еще пример задания:Р-00. Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110). Определите, какое число передавалось по каналу в виде 01010100100111100011? Решение: сначала разберемся, как закодированы числа в примере; очевидно, что используется код равномерной длины; поскольку 2 знака кодируются 10 двоичными разрядами (битами), на каждую цифру отводится 5 бит, то есть 2 → 00101 и 3 → 00110 как следует из условия, четыре первых бита в каждой последовательности – это двоичный код цифры, а пятый бит (бит четности) используется для проверки и рассчитывается как «сумма по модулю два», то есть остаток от деления суммы битов на 2; тогда 2 = 00102, бит четности (0 + 0 + 1 + 0) mod 2 = 1 3 = 00112, бит четности (0 + 0 + 1 + 1) mod 2 = 0 но бит четности нам совсем не нужен, важно другое: пятый бит в каждой пятерке можно отбросить! разобъем заданную последовательность на группы по 5 бит в каждой: 01010, 10010, 01111, 00011. отбросим пятый (последний) бит в каждой группе: 0101, 1001, 0111, 0001. это и есть двоичные коды передаваемых чисел: 01012 = 5, 10012 = 9, 01112 = 7, 00012 = 1. таким образом, были переданы числа 5, 9, 7, 1 или число 5971. Ответ: 5971. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
