Кольца Ньютона. Кольца Ньютона
 Скачать 23.54 Kb. Скачать 23.54 Kb.
|
|
Кольца Ньютона. Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны. Рис.7. 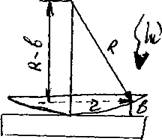 Наблюдаются кольца Ньютона и с системой соприкасающихся плосковогнутой и плосковыпуклой линз с большим радиусом кривизны, причем радиус кривизны плосковогнутой линзы должен быть больше радиуса кривизны плосковыпуклой линзы. Роль тонкого клина, от поверхности которого отражаются когерентные волны, играет воздушный зазор между стеклянной пластинкой и линзой (рис.7). Вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают. Луч света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора. Отраженные лучи когерентны и при их наложении возникают полосы равной толщины. При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении - эллипсов. Определим оптическую разность хода отраженных лучей и найдем радиусы колец Ньютона при нормальном падении света на пластину. В этом случае sinQ1 = О и D равна удвоенной толщине зазора (предполагается n0 = 1). Из рис. 7 следует, что R2 = (R – b)2 + r2 » R2 – 2Rb + r2, (12) где R - радиус кривизны линзы, r - радиус окружности, всем точкам которой соответствует одинаковый зазор толщиной b. Считаем b2 < 2Rb, тогда из (12) получим, что b = г2/2R. Чтобы учесть возникающее при отражении от стеклянной пластинки изменение фазы на p, нужно к D = 2b = r2/R прибавить lо/2. Тогда оптическая разность хода лучей окончательно запишется так D = r2/R + lо/2. (13) В точках, для которых D = m'lо = 2m'(lо/2), возникают максимумы, в точках, для которых D = (m' + 1/2)lо =(2m'+ 1)(lо/2),- минимумы интенсивности. Оба условия можно объединить в одно: D = mlо/2, m = 1, 2, 3, … (13а) причем четным значениям m будут соответствовать максимумы, а нечетным -минимумы интенсивности. Приравняв(13) и (13а) и разрешив получившееся уравнение относительно r, найдем радиусы светлых и темных колец Ньютона: rm = ÖRlо(m- 1)/2, (m =1,2,3,...). (14) Четным значениям m соответствуют радиусы светлых колец, нечетным m - радиусы темных колей. Значению m =1 соответствует точка касания пластинки и линзы (г = 0). В этой точке наблюдается минимум интенсивности, обусловленный изменением фазы волны на p при отражении световой волны от стеклянной пластинки. Измеряя расстояния между полосами интерференционной картины для тонких пластин или радиусы колец Ньютона, можно определить длины волн световых лучей и, наоборот, при известной длине волны lо найти радиус кривизны линзы R. Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны, появляющейся при отражении света от стеклянной пластины. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на l0/2, т.е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот. При освещении оптической системы не монохроматическим, а белым светом наблюдается совокупность смещенных друг относительно друга интерференционных полос (колец), образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску. |
