Кольца Ньютона
 Скачать 355 Kb. Скачать 355 Kb.
|
|
Компьютерная лабораторная работа «Кольца Ньютона» Цель работы 1) познакомится с кольцами Ньютона, с интерференцией – причиной их возникновения; выяснить, чем отличается картина в отражённом и проходящем свете, какова роль показателей преломления линзы и пластинки и среды между ними; 2) определить радиус кривизны линзы, используя линейную зависимость квадратов радиусов светлых колец Оборудование и программное обеспечение персональный компьютер с операционной системой Windows; программа «Newton_new». Подготовка к работе По настоящему описанию и литературе из библиографического списка изучить следующие вопросы: 1. Что такое интерференция? Как возникает интерференция в тонких плёнках? 2. Как получаются кольца Ньютона? Нарисуйте схему. 3. Получить связь между радиусом колец Ньютона r, радиусом кривизны выпуклой поверхности линзы R и толщиной зазора bмежду линзой и пластиной. 4. Получить формулу, устанавливающую связь между 5. Почему для 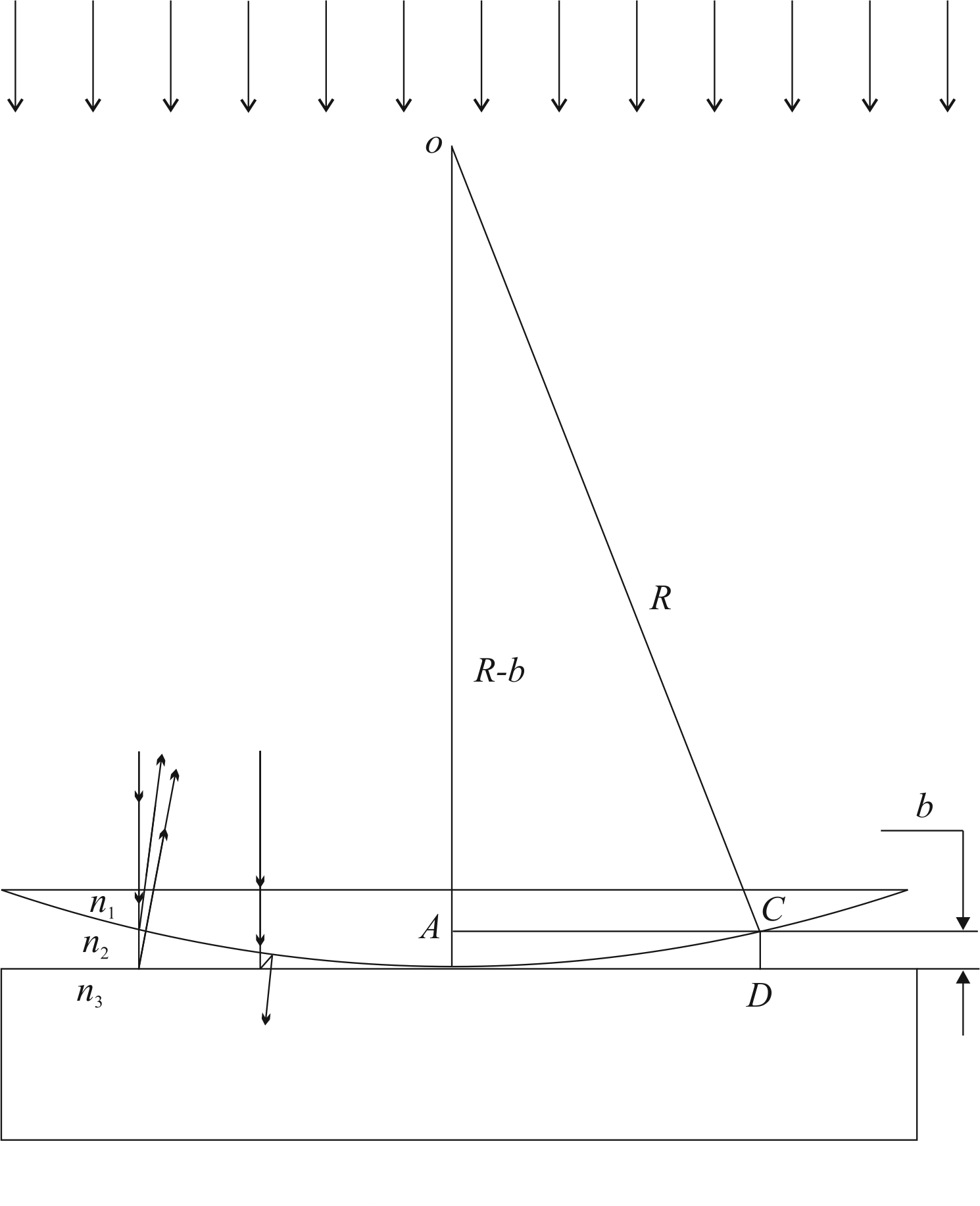 Рис. 1.1. Схема установки для наблюдения колец Ньютона Вопросы для допуска к лабораторной работе 1. Что такое интерференция света? 2. Что такое некогерентные волны? Когерентные волны? 3. Каковы условия максимума и минимума на разность фаз? 4. Что такое оптическая разность хода? 5. Запишите условия максимума и минимума на оптическую разность хода. Теория метода измерений На рис. 1 изображена схема установки для наблюдения колец Ньютона. Радиус R кривизны выпуклой поверхности линзы в опыте Ньютона был около 10 м, поэтому ясно, что масштаб на этом рисунке не выдержан. Отрезок AC на рисунке – радиус r кольца Ньютона. Радиус линзы R велик по сравнению с r – радиусом колец, и поэтому угол падения света на внутреннюю поверхность линзы Связь между радиусом колец Ньютона r, радиусом кривизны выпуклой поверхности линзы R и толщиной зазора b между верхней поверхностью плоскопараллельной стеклянной пластинки и нижней поверхностью линзы найдём по теореме Пифагора из прямоугольного треугольника ACO (рис.1): Раскроем скобки: 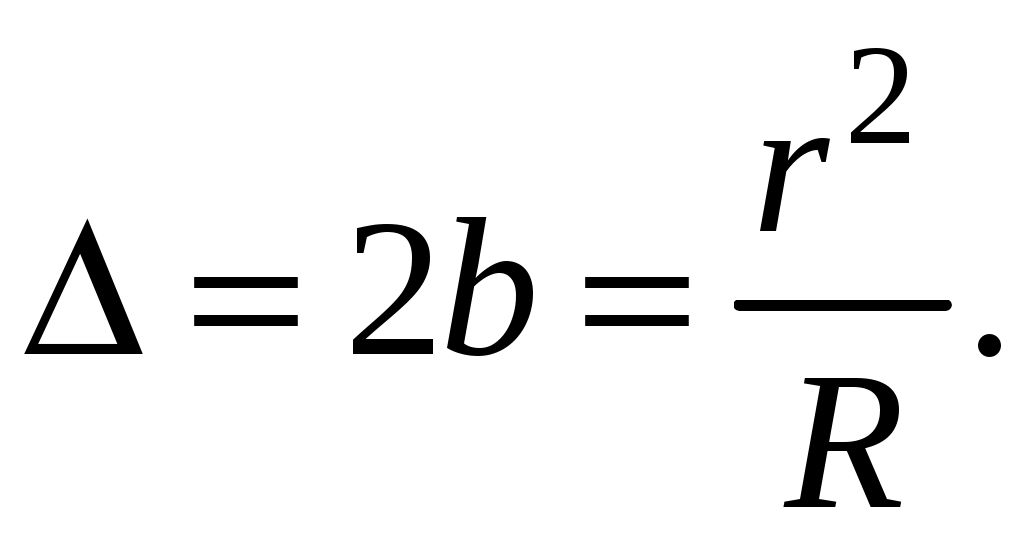 (1.1) (1.1)Оптическая разность хода Рассмотрим четыревозможные ситуации, приведённые на рис.1.2. 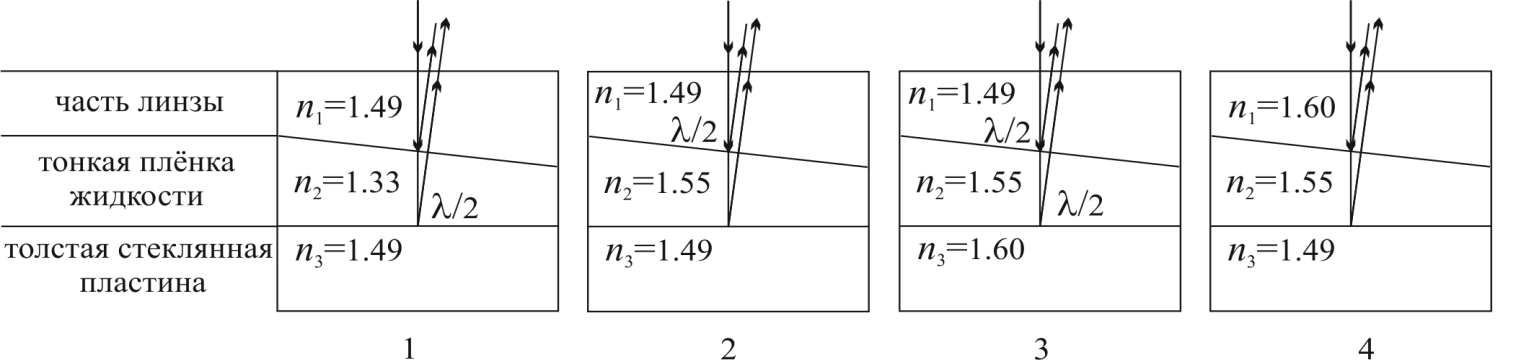 Рис. 1.2. Различные возможные соотношения показателей преломления линзы, прослойки и пластины На этом рисунке изображены четыре варианта схемы установки для наблюдения колец Ньютона. У Ньютона тонкой плёнкой был воздух, в нашей программе в качестве прослойки с показателем преломления n2 используются жидкости с показателями преломления от 1,33 (вода) до 1,95 (фосфор) (6 различных значений, не считая воздуха). В качестве показателей преломления n1 и n3могут быть выбраны значения, характерные для стекла – от 1,49 (лёгкий крон) до 2,19 (сверхтяжёлый флинт), а также алмаз – n1 = 2,42. На рис. 1.2 изображен ход лучей в отражённом свете при различныхсочетаниях показателей преломления. 1. В первом случае отражение от более плотной среды происходит на границе n2–n3, с добавлением к 2. Во второмслучаеотражение отболее плотной среды происходит на границеn1 –n2, здесь возникает добавка к разности хода 3. В третьем случае обе границы n1 –n2 и n2–n3 отражают со скачком разности хода на 4. В четвёртомслучае картина также начинается со светлогопятна, потому что оба отражения происходят от оптически менее плотной среды, и никаких скачков разности хода не наблюдается. Получим формулу для радиусов колец Ньютона в отражённом свете, когда В этом случае оптическая разность хода 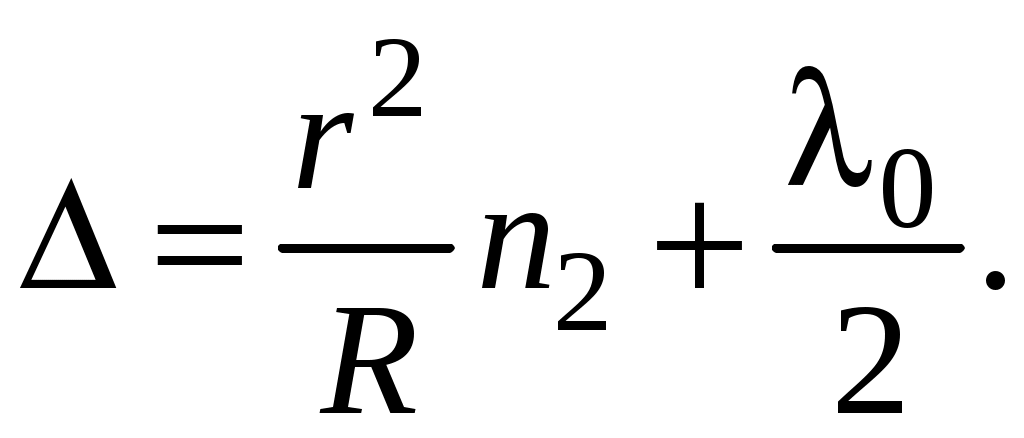 (1.2) (1.2)Для светлых колец используем условие максимума при интерференции двух волн: Из (1.2) и (1.3) получим: 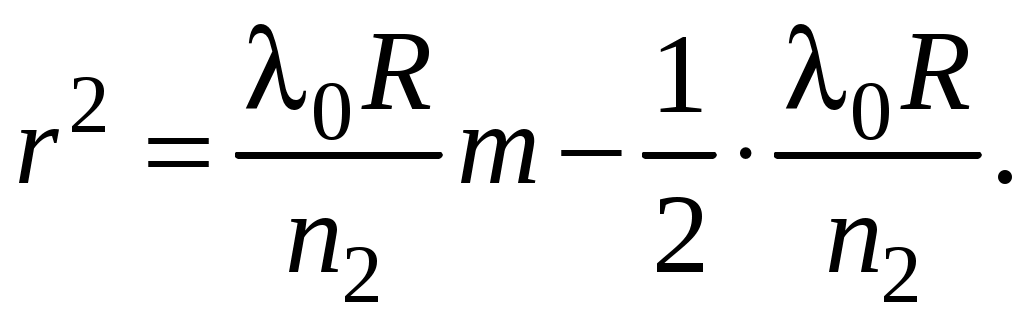 (1.4) (1.4)и 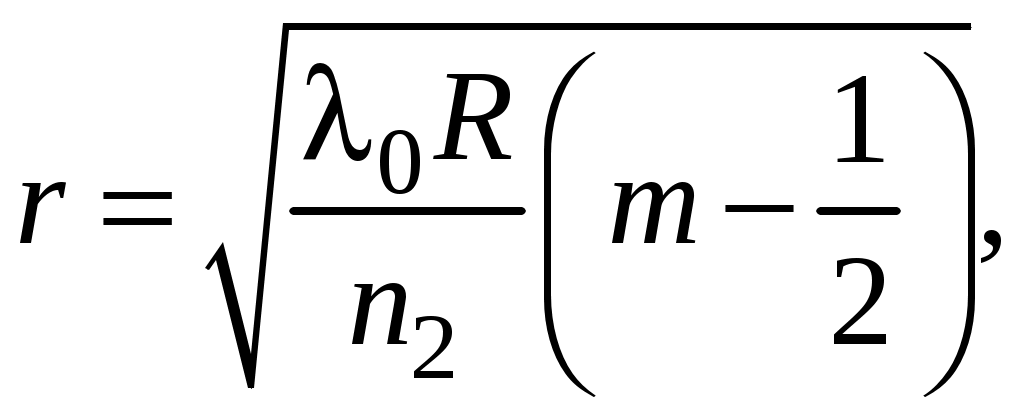 (1.5) (1.5)где m = 1, 2, 3… – номер светлого кольца. Метод определения радиуса кривизны линзы Функцию (1.4) можно рассматривать как линейную зависимость квадратов радиусов колец 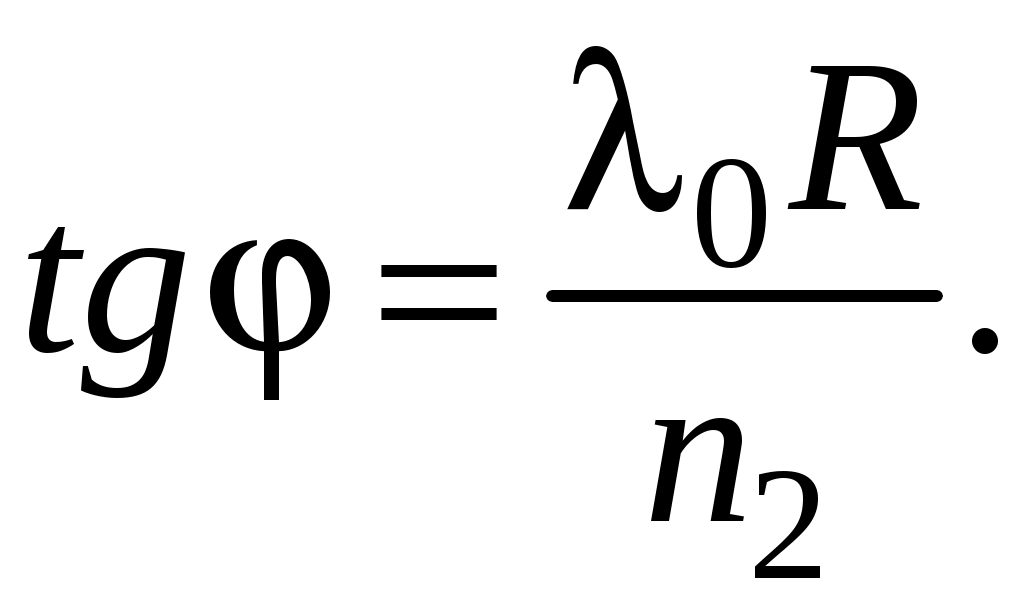 (1.6) (1.6)С другой стороны, тангенс угла наклона графика линейной функции – это отношение приращения функции к приращению аргумента: 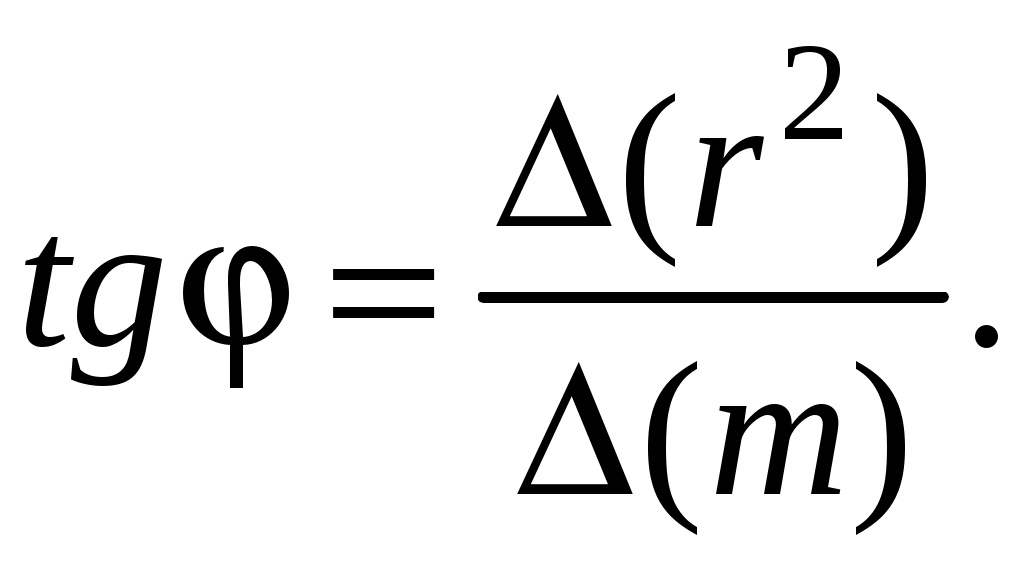 (1.7) (1.7)Приравнивания правые части формул (1.6) и (1.7), получим формулу для определения радиуса кривизны линзы: 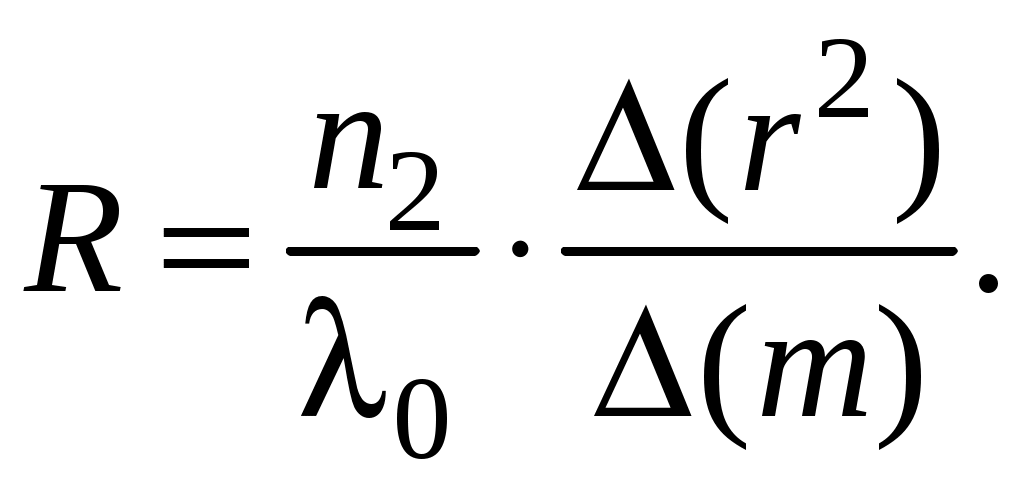 (1.8) (1.8)Задание 1 Знакомство с виртуальной демонстрацией колец Ньютона Порядок выполнения задания 1 1.Запустите программу «Newton_new», хорошо рассмотрите рисунки на главнойстранице экрана. 2. Выберите в строке меню пункт «Демонстрация». Нажимая на пункты «Кольца в отражённом свете», «Кольца в проходящем свете», ознакомьтесь с соответствующими интерференционными картинами. Чем они различаются? 3. Управляющий элемент «Длина волны 4. Управляющий элемент «Показатели преломления», находящийся у правого края окна программы и состоящий из трёх бегунков, позволяет изменять показатель преломления линзы n1 и пластинки n3 в диапазоне от 1,49 до 2,42, а также показатель преломления прослойки между линзой и пластинкой n2 в диапазоне от 1,00 до 1,95. Перемещая бегунки при помощи мыши, установите значения показателей преломления, соответствующие рис. 1.2, последовательно воспроизведя все четыре комбинации. Зарисуйте и сравните полученные интерференционные картины. Сделайте выводы. Задание 2 Определение радиуса кривизны линзы Порядок выполнения задания 2 1. Перейдите в раздел «Лабораторная работа», выбрав соответствующий пункт меню, а в нём – подпункт «Интерференционная картина». На экране появятсякольца в отражённом свете. Сначала необходимо выбрать и записать в таблицу (табл. 1) значения длины волны света и показателей преломления линзы, прослойки и пластинки (конкретные численные значения могут быть указаны преподавателем). Таблица 1.1 Определение радиуса кривизны линзы
2. Нажмите на кнопку «Ввести радиусы», расположенную в правом нижнем углу окна программы, и в появившемся окне введите (в миллиметрах) радиусы пяти первых светлых колец Ньютона, определяя их на глаз с точностью до сотых долей миллиметра по имеющейся на экране шкале. Запишите эти значения, также, в табл. 1. После этого нажмите кнопку «Подтвердить». 3. Перейдите к определению радиуса кривизны выпуклой поверхности линзы R. Для этого в пункте меню «Лабораторная работа» выберите подпункт «Определение радиуса кривизны линзы». Вы увидите на экране автоматически построенный компьютером по введенным Вами значениям график зависимости квадратов радиусов светлых колец 4. Нажмите кнопку «Проверить», в появившемся окне введите полученное Вами значение радиуса кривизны линзы. После этого программа выдаст правильный ответ и выставит Вам оценку. 5. Сделайте вывод, как зависят радиусы колец Ньютона от их номеров. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Тюшев А.Н. Физика в конспективном изложении. Ч. 2. Колебания. Волны.Волновая оптика. – Новосибирск, СГГА, 2002.– С. 62–63. 2. Тюшев А.Н., Дикусар Л.Д. Курс лекций по физике. Ч. 3. Колебания и волны. Волновая оптика: учеб.пособие. – Новосибирск: СГГА,2011. – С. 103–107. 3. Трофимова Т.И. Курс физики: учеб.пособие. – М.: Академия, 2015. – С. 324–327. Приложение 1 Образец оформления титульного листа
| |||||||||||||||||||||||||||||||||||||||||||||
