cosy.
6.
ex.
X.
0.
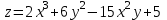 функциясы үшін А(1;-1) нүктесіндегі функциясы үшін А(1;-1) нүктесіндегі 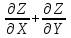 өрнегінің мәнін тап: өрнегінің мәнін тап:
9
19
0
-9
- 1
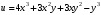 функциясы үшін функциясы үшін 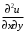 -ті тап: -ті тап:
6(x+y)
3x+4y
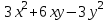
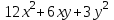
24x+6y
x=y=1 болғанда 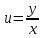 функциясы үшін функциясы үшін 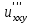 -ті тап: -ті тап:
2.
–6.
3.
0.
6.
x=y=1 болғанда 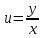 функциясы үшін функциясы үшін 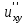 -ті тап: -ті тап:
–1.
2.
0.
1.
3.
у'=cos3x дифференциалдық теңдеуді шеш.
 sin3x+C. sin3x+C.
sin3x+C.
-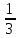 sin3x+C. sin3x+C.
3sin3x+C.
-3sin3x+C.
у'=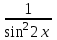 дифференциалдық теңдеуді шеш. дифференциалдық теңдеуді шеш.
-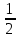 ctg2x+С. ctg2x+С.
ctg2x+С.
-2tg2x+C.
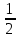 ctg2x+C. ctg2x+C.
tg2x+C.
F(x, y, y’,…,y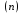 )=0 түріндегі дифференциалдық теңдеу қандай теңдеу деп аталады: )=0 түріндегі дифференциалдық теңдеу қандай теңдеу деп аталады:
n-ші ретті.
1-ші ретті.
2-ші ретті.
3-ші ретті.
n-1-ші ретті.
Бірінші ретті теңдеуді шеш 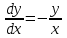 : :
y=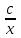 . .
y=c*x.
y=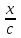 . .
y=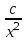 . .
y=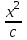 . .
Жалпы интегралдың геометриялық мағынасы:
қисықтар жиынтығы.
бір қисық сызық.
екі қисық сызық.
үш қисық сызық.
төрт қисық сызық.
(1+x)*ydx+(1-y)*xdy=0 теңдеуін шешіңдер:
ln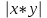 +x-y=c. +x-y=c.
ln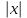 +x-y=c. +x-y=c.
ln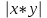 +x+y=c. +x+y=c.
ln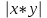 -x-y=c. -x-y=c.
ln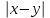 +x*y=c. +x*y=c.
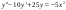 сызықтық біртекті емес дифференциалдық теңдеудің дербес шешімінің түрін анықта: сызықтық біртекті емес дифференциалдық теңдеудің дербес шешімінің түрін анықта:
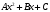
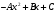
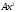
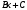
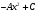
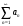 , мүшелірі оң санды қатардың, , мүшелірі оң санды қатардың, 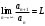 - Даламбер белгісі бойынша жинақталу егер : - Даламбер белгісі бойынша жинақталу егер :
L<1.
L>1.
L=1.
L=0.
L= -1.
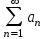 санды қатардың қажеттілік шарты: санды қатардың қажеттілік шарты:
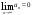 . .
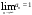 . .
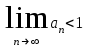 . .
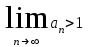 . .
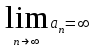 . .
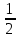 + +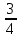 + +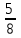 + +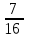 +... қатарын +... қатарын 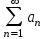 түрінде жаз: түрінде жаз:
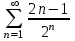 . .
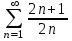 . .
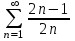 . .
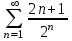 . .
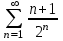 . .
1+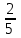 + +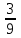 + +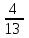 +... қатарын +... қатарын 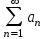 түрінде жаз, мұндағы түрінде жаз, мұндағы 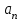 -қатардың жалпы мүшесі. -қатардың жалпы мүшесі.
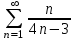 . .
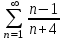 . .
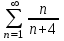 . .
<variant>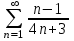 . .
<variant>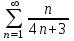 . .
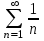 қатары қатары
Гармоникалық.
Коши.
Даламбер
Логарифмдік.
Бигармониялық.
Жинақталу интервалын тап: 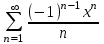 . .
(-1;1).
-1.
1.
(0;1).
0
Жинақталу интервалын тап: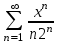 . .
(-2;2).
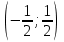 . .
-2.
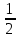 . .
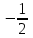 . .
Жинақталу интервалын тап: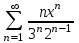 . .
(-6;6)
-6.
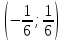
6.
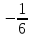
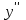 -тап , егер -тап , егер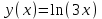 : :
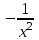
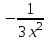
3.
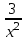
3lnx.
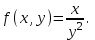 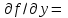 : :
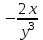 . .
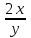 . .
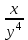 . .
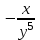 . .
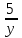 . .
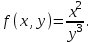 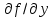 : :
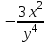 . .
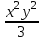 . .
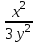 . .
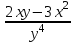 . .
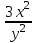 . .
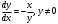 теңдеуінің жалпы шешімін тап: теңдеуінің жалпы шешімін тап:
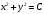
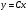
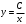
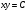
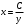
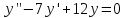 біртекті дифференциалдық теңдеудің жалпы шешімін тап: біртекті дифференциалдық теңдеудің жалпы шешімін тап:
y=C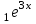 + C + C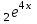 . .
y=C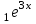 + C + C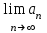 . .
y=C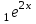 + C + C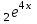 . .
y=C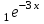 + C + C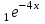 . .
y=C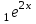 + C + C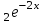 . .
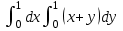 интегралын есептеңіз: интегралын есептеңіз:
1
2
-2
-1
0
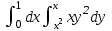 интегралынесептеңіз: интегралынесептеңіз:
1/40
1/20
1
3/40
-1/40
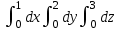 интегралынесептеңіз: интегралынесептеңіз:
6
0,6
7
0,3
10
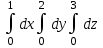 интегралынесептеңіз: интегралынесептеңіз:
6
1
5
8
2
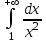 меншіксіз интегралы неге тең? меншіксіз интегралы неге тең?
1
0
-1
2
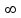
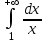 меншіксіз интегралы неге тең? меншіксіз интегралы неге тең?
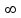
0
1
-1
2
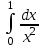 меншіксіз интегралы неге тең? меншіксіз интегралы неге тең?
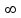
0
1
-1
2
Есепте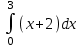 : :
10,5
21
0,5
20
0,1
Есепте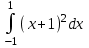 : :
8/3
5/3
0
–8/3
1/3
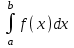 шамасының мағынасы? шамасының мағынасы?
фигураның ауданы
функцияның кесіндідегі орта мәні
доғаның ұзындығы
фигураның көлемі
жұмыс
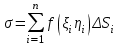 … деп аталады … деп аталады
интегралдық қосынды
интегралдық көбейткіш
вектордың қосындысы
квадраттық қосынды
кубтық қосынды
Есепте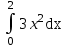 . .
8
–8
–6
6
3
Есепте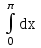 . .
π
0
–π
x
x + C
Анықталған интегралдың геометриялық мағынасы, бұл:
қисық сызықты трапецияның ауданы
дөңгелектің ауданы
шаршының ауданы
тіктөртбұрыш ауданы
сәйкес пластинаның ауданы
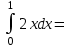
1
0
– 1
2
–2
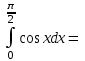
1
0
–1
2
–2
Z=arctg(xy) функциясының 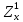 (1;2) мәнін тап. (1;2) мәнін тап.
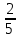
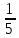
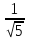
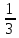
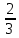
Z=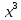 +4 +4 y-6x y-6x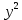 + +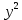 функциясының функциясының 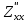 туындысын тап. туындысын тап.
6x+8y
6x-2y
8x-12y+2
14x-4y
3 +8xy-6 +8xy-6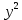
Z=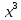 +4 +4 y-6x y-6x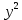 + +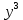 функциясының функциясының 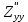 туындысын тап. туындысын тап.
-12x+6y
4 -12x+6y -12x+6y
8x-12y
-12x+6xy
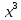 +4 +4 -12x -12x
ƒ(x,y)=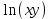 функциясының dZ(1;1) туындысын тап. функциясының dZ(1;1) туындысын тап.
dx+dy
dx-dy
dx+2dy
2dx-dy
3dx-2dy
Z=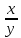 функциясының dZ дифференциалын тап. функциясының dZ дифференциалын тап.
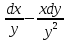
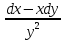
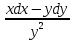
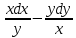
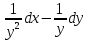
Z= +xy+ +xy+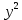 -2x-y функцияның кризистік нүктесін тап. -2x-y функцияның кризистік нүктесін тап.
(1;0)
(0;1)
(1;1)
(0;0)
(-1;-1)
Z=(x-1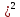 -2 -2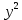 функцияның экстремум нүктесін тап. функцияның экстремум нүктесін тап.
экстремумы жоқ
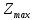 =0 =0
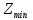 =0 =0
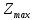 =1 =1
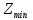 =1 =1
Z=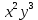 функциясы берілген.Табу керек dZ. функциясы берілген.Табу керек dZ.
2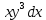 +3 +3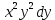
2x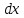 +3 +3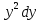
3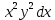 +2 +2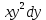
3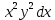 +3 +3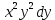
6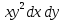
Z= -xy+ -xy+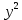 +3x-2y+1 функциясының dZ(1;1) мәнін тап. +3x-2y+1 функциясының dZ(1;1) мәнін тап.
4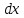 - -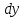
4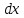 + +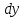
-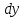
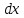 - -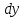
4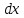 -3 -3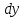
Z=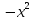 - -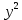 +xy+3y кризистік нүктесін тап. +xy+3y кризистік нүктесін тап.
(1;2)
(2;1)
(-1;2)
(-1;-2)
(1;-2)
Мына xy'-y=0 теңдеуін шеш.
y=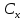
y=x+C
y=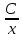
y=C
y=x
y'=ycosx теңдеуін шеш.
y=C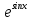 y=C y=C
y=C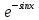 y= y= +C +C
y=sinx+C y=2x+C
y=-sinx+C y=C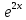
y=Csinx x=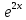 +C +C
2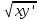 =y теңдеуін шеш. =y теңдеуін шеш.
y=C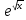
y=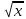 +C +C
y=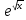 +C +C
y=C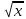
y=C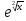
y'-2y=0 теңдеуін шеш.
y=С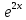
y=2x+C
y=Cx+2
y=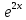 +C +C
y=C
xy'=2y теңдеуін шеш.
y=C
y= +C +C
y=2x+C
y=C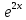
x=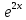 +C +C
2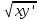 =y теңдеуін шеш. =y теңдеуін шеш.
y=C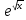
y=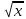 +C +C
y=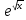 +C +C
y=C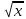
y=C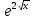
( +3)y'=xy теңдеуін шеш. +3)y'=xy теңдеуін шеш.
y=C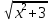
y=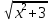 +C +C
y=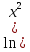 +3)+C +3)+C
y=C( +3) +3)
y=C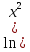 +3) +3)
y'=2xy теңдеуін шеш.
y=C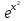
y=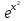
y=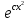
y=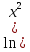 +C) +C)
y=2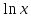 +C +C
y'=ytgx теңдеуін шеш.
y=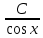
y=C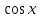
y=-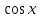 +C +C
y=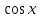 +C +C
y=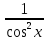 +C +C
xy'=1 теңдеуінің x=e болғанда y=3 шартты қанағаттандыратын шешімін тап.
y=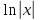 +2 +2
y=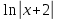
y=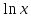 +2 +2
y=4-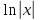
y=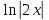
y'=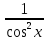 теңдеуінің x= теңдеуінің x=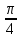 болғанда y=2 шешімін тап. болғанда y=2 шешімін тап.
y=3-ctgx
y=1+ctgx
y=2-ctgx
y=3-tgx
y=1+tgx
y'=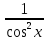 теңдеуінің x= теңдеуінің x=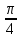 болғанда y=3 шешімін тап. болғанда y=3 шешімін тап.
y=tgx+2
y=4-tgx
y=3tgx
y=ctgx+2
y=4-ctgx
y″-4y'=0 теңдеуін шеш.
y=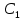 + +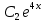
y=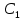 + +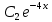
y=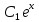 + +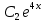
y=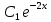 + +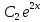
y=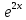 ( (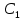 + +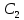 x) x)
y″+9y=0 теңдеуін шеш.
y=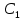 cos3x+ cos3x+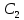 sin3x sin3x
y=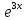 ( (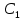 cosx+ cosx+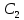 sinx) sinx)
y=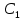 + +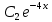
y=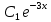 + +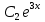
y=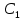 + +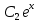
Мына 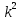 +1=0 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет. +1=0 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.
y″+y=0
y″+y'=0
y″+1=0
2y″+1=0
2y″+y=0
Мына 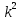 +k=0 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет. +k=0 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.
y″+y'=0
y″+y=0
y″+1=0
y″+y'+1=0
y″+y'+y=0
Мына 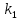 =-1, =-1, 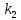 =2 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет. =2 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.
y″-y'-2y=0
y″+y'-2y=0
y″+y'+2y=0
y″-y'+2y=0
y″+2y'-y=0
Мына k=2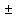 i сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет. i сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.
y″-4y'+5y=0
y″+4y'+5y=0
y″-3y'+2y=0
y″+3y'+2y=0
y″+2y'+y=0
Сандық қатарлар жинақты болады, егер
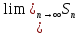 =S =S
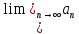 =0 =0
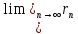 =0 =0
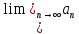 <1 <1
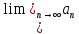 >1 >1
Сандық қатарлардың жинақты болуының қажетті шартын көрсет
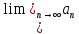 =0 =0
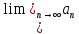 =s =s
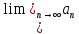 < <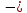 1 1
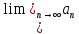 >1 >1
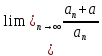 <1 <1
Мына 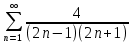 қатардың қосындысын тап? қатардың қосындысын тап?
S=2 және қатар жинақтары
қатар жинақсыз
s=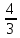
S=0
s=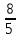
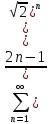 қатарының жинақтылығын зертте қатарының жинақтылығын зертте
жинақты
жинақсыз
шартты жинақты
абсолютті жинақты
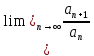 >1 >1
Қатардың жинақтылығын зертте 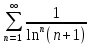
жинақты
жинақсыз
шартты жинақты
абсолютті жинақты
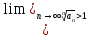
Қатардың жинақтылығын зертте 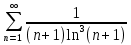
жинақты
жинақсыз
шартты жинақты
абсолютті жинақты
c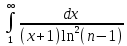
Кезек таңбалы қатардың жинақтылығын зертте 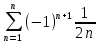
шартты жинақты
абсолютті жинақты
жинақсыз
жинақты
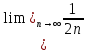 =0 =0
Қатардың жинақтылық облысын тап 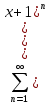
қатар [-3;1) аралығында жинақты
-3
-3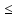 x x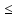 1 1
-3 1
-2
Қатардың жинақтылық облысын тап 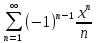
-1 1
-1≤x<1
-1≤x≤1
-1
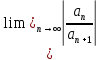 >1 >1
|
 Скачать 0.95 Mb.
Скачать 0.95 Mb.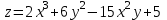
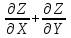 өрнегінің мәнін тап:
өрнегінің мәнін тап: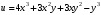
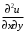 -ті тап:
-ті тап: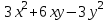
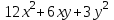
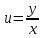 функциясы үшін
функциясы үшін 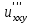 -ті тап:
-ті тап: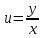 функциясы үшін
функциясы үшін 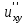 -ті тап:
-ті тап:
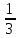 sin3x+C.
sin3x+C.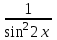 дифференциалдық теңдеуді шеш.
дифференциалдық теңдеуді шеш. ctg2x+С.
ctg2x+С. 
 )=0 түріндегі дифференциалдық теңдеу қандай теңдеу деп аталады:
)=0 түріндегі дифференциалдық теңдеу қандай теңдеу деп аталады: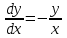 :
: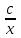 .
. 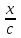 .
.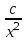 .
.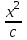 .
.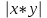 +x-y=c.
+x-y=c. 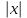 +x-y=c.
+x-y=c.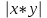 +x+y=c.
+x+y=c.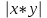 -x-y=c.
-x-y=c.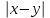 +x*y=c.
+x*y=c.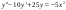
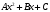
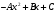
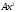
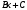
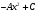
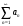
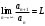 - Даламбер белгісі бойынша жинақталу егер :
- Даламбер белгісі бойынша жинақталу егер :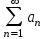
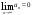
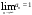
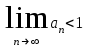
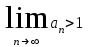
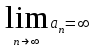
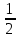
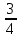 +
+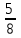 +
+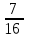 +... қатарын
+... қатарын 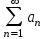 түрінде жаз:
түрінде жаз: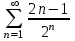 .
. 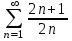 .
. 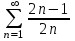 .
. 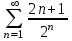 .
. 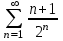
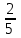 +
+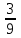 +
+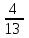 +... қатарын
+... қатарын 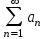 түрінде жаз, мұндағы
түрінде жаз, мұндағы 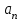 -қатардың жалпы мүшесі.
-қатардың жалпы мүшесі.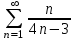
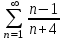
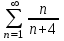 .
. 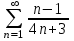 .
. 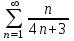 .
. 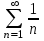
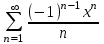 .
.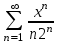 .
.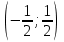
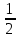
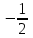
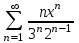 .
.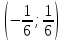
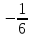
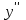
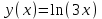 :
: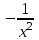
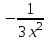
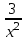
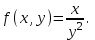
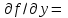
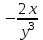
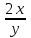
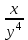
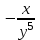
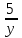
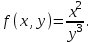
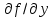
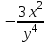
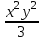
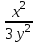
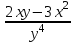
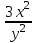
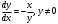
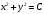
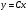
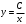
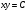
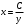
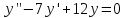
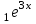 + C
+ C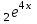 .
.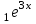 + C
+ C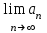 .
.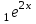 + C
+ C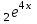 .
.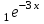 + C
+ C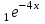 .
.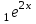 + C
+ C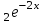 .
.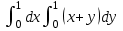
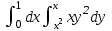
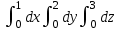
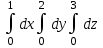
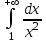
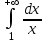
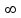
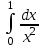
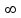
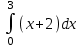 :
: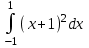 :
: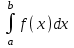
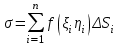
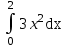 .
.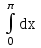 .
.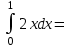
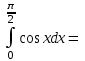
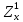 (1;2) мәнін тап.
(1;2) мәнін тап.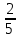
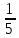
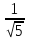
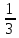
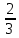
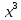 +4
+4 y-6x
y-6x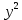 +
+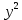 функциясының
функциясының 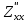 туындысын тап.
туындысын тап. +8xy-6
+8xy-6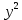
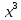 +4
+4 y-6x
y-6x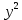 +
+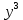 функциясының
функциясының 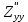 туындысын тап.
туындысын тап. -12x+6y
-12x+6y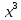 +4
+4 -12x
-12x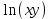 функциясының dZ(1;1) туындысын тап.
функциясының dZ(1;1) туындысын тап.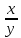 функциясының dZ дифференциалын тап.
функциясының dZ дифференциалын тап.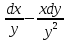
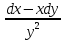
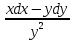
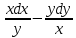
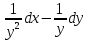
 +xy+
+xy+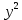 -2x-y функцияның кризистік нүктесін тап.
-2x-y функцияның кризистік нүктесін тап.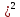 -2
-2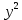 функцияның экстремум нүктесін тап.
функцияның экстремум нүктесін тап.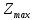 =0
=0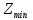 =0
=0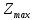 =1
=1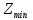 =1
=1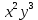 функциясы берілген.Табу керек dZ.
функциясы берілген.Табу керек dZ.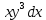 +3
+3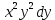
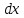 +3
+3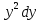
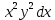 +2
+2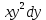
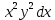 +3
+3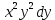
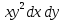
 -xy+
-xy+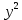 +3x-2y+1 функциясының dZ(1;1) мәнін тап.
+3x-2y+1 функциясының dZ(1;1) мәнін тап.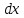 -
-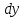
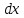 +
+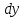
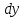
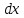 -
-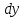
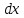 -3
-3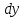
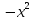 -
-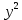 +xy+3y кризистік нүктесін тап.
+xy+3y кризистік нүктесін тап.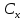
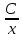

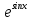

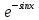
 +C
+C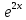
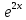 +C
+C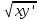 =y теңдеуін шеш.
=y теңдеуін шеш.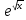
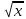 +C
+C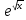 +C
+C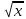
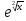
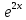
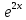 +C
+C

 +C
+C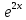
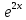 +C
+C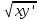 =y теңдеуін шеш.
=y теңдеуін шеш.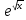
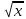 +C
+C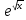 +C
+C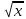
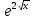
 +3)y'=xy теңдеуін шеш.
+3)y'=xy теңдеуін шеш.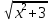
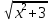 +C
+C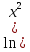 +3)+C
+3)+C +3)
+3)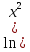 +3)
+3)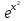
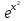
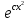
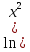 +C)
+C)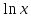 +C
+C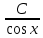
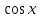
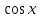 +C
+C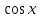 +C
+C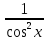 +C
+C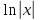 +2
+2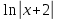
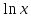 +2
+2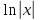
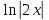
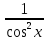 теңдеуінің x=
теңдеуінің x=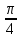 болғанда y=2 шешімін тап.
болғанда y=2 шешімін тап.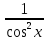 теңдеуінің x=
теңдеуінің x=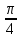 болғанда y=3 шешімін тап.
болғанда y=3 шешімін тап.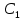 +
+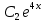
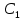 +
+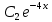
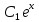 +
+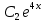
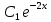 +
+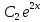
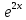 (
(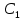 +
+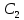 x)
x)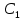 cos3x+
cos3x+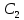 sin3x
sin3x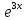 (
(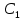 cosx+
cosx+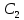 sinx)
sinx)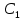 +
+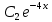
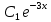 +
+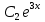
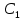 +
+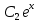
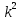 +1=0 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.
+1=0 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.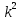 +k=0 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.
+k=0 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет. 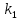 =-1,
=-1, 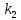 =2 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.
=2 сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.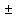 i сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет.
i сипаттамалық теңдеуге сәйкес келетін дифференциалдық теңдеуді көрсет. 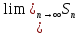 =S
=S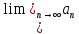 =0
=0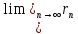 =0
=0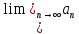 <1
<1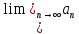 >1
>1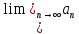 =0
=0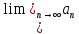 =s
=s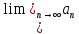 <
<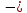 1
1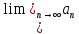 >1
>1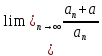 <1
<1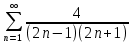 қатардың қосындысын тап?
қатардың қосындысын тап?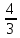
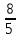
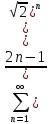 қатарының жинақтылығын зертте
қатарының жинақтылығын зертте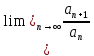 >1
>1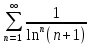
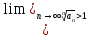
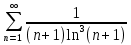
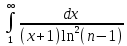
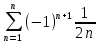
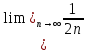 =0
=0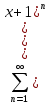
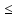 x
x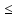 1
1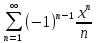
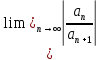 >1
>1