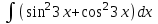
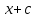
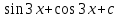
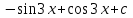
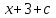
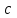
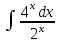 = =
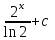
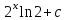
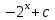
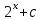
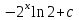
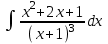 = =
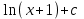
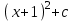
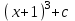
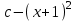
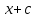
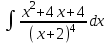 = =
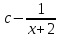
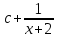
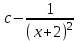
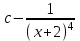
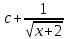
Есепте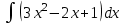
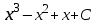
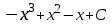
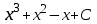
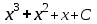
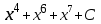
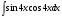 = =
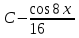
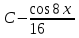
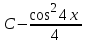
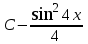
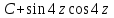
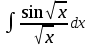 = =
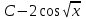
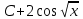
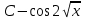
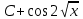
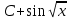
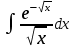 = =
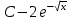
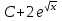
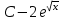
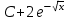
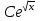
Табыңыз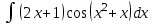
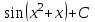
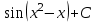
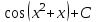
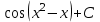
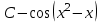
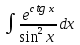 = =
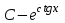
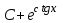
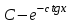
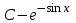
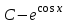
Есепте: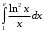 : :
1/3.
1.
–1/3.
2/3.
–2/3.
Есепте: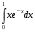 : :
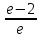 . .
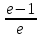 . .
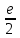 . .
e – 1.
e – 2.
Анықталмаған интегралды тап: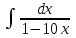 . .
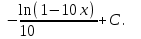
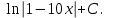
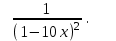
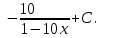
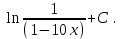
х = 5, у = 0, у =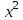 сызықтарымен шектелген фигураның ауданын тап: сызықтарымен шектелген фигураның ауданын тап:
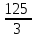 . .
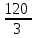 . .
125.
1/3.
120.
х = 0, х = , у = 0, у = sinx сызықтарымен шектелген фигураның ауданын тап:
2.
1.
–1.
0.
–2.
х = 2, у = 0, у = 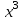 сызықтарымен шектелген фигураның ауданын тап: сызықтарымен шектелген фигураның ауданын тап:
4.
2.
½.
¼.
0.
Есепте: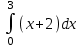 : :
10,5.
21.
0,5.
20.
0,1.
Интегралды тап: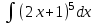 : :
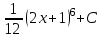 . .
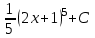 . .
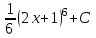 . .
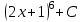 . .
½ 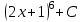 . .
Есепте: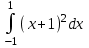 : :
8/3.
5/3.
0.
–8/3.
1/3.
<question>у = 0, у = 3х – 3, х = 2 сызықтарымен шектелген фигураның ауданын тап:
3/2.
2.
3.
½.
6.
у = 0, у = х, х = 4 сызықтарымен шектелген фигураның ауданын тап:
8.
2.
4.
6.
1.
Анықталмаған интегралды тап: 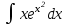 . .
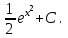
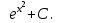
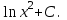
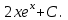
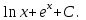
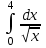 анықталған интегралдың мәні: анықталған интегралдың мәні:
4
0
2
1
-2
Есепте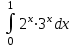 : :
5/ ln 6.
6ln 6.
4ln 6.
5ln 6.
ln 6.
Есепте: 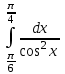 : :
1 - 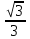 . .
1 + 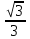 . .
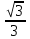 . .
-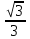
1 + 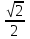 . .
Есепте: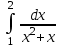 : :
ln 4/3.
ln 3.
ln 1/3.
ln 5/3
ln 2.
Есепте: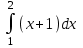 : :
5/2.
½.
3/2.
0.
2.
Ньютона-Лейбниц формуласы:
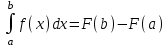 . .
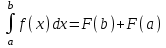 . .
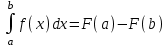 . .
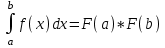 . .
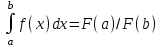 . .
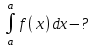 : :
0.
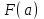 . .
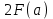 . .
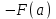 . .
1.
Анықталған интегралдың келесі қасиетін жалғастырып аяқта. Интегралдау шектерінің орнын ауыстырғанда:
интегралдың таңбасы өзгереді.
интеграл екі еселенеді.
интеграл өзгермейді.
интеграл нөлге тең болады.
интегралдың таңбасы өзгереді және интеграл өзгермейді.
Денені Ох өсін айналдыра бұрғаннан пайда болған дененің көлемі қандай формула арқылы өрнектеледі?:
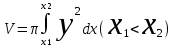 . .
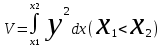 . .
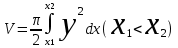 . .
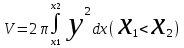 . .
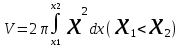
Денені Оу өсін айналдыра бұрғаннан пайда болған дененің көлемі қандай формула арқылы өрнектеледі ?:
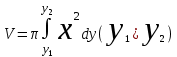 . .
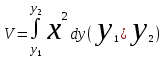 . .
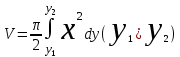 . .
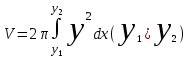 . .
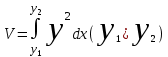 . .
Сөйлемді аяқта: егер 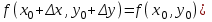 болса, онда болса, онда 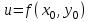 функциясы функциясы 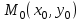 нүктесінде … болады: нүктесінде … болады:
дифференциалданатын.
үзілісті.
экстремальды.
үзіліссіз.
шексіз аз.
Егер u=f(x,y) функциясының жоғарғы ретті үзіліссіз аралас туындылары бар болса, онда келесі қатынас орындалады:
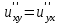 . .
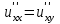 . .
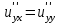 . .
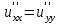 . .
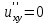 . .
Егер 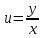 болса, болса, 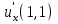 - ті есепте: - ті есепте:
–1.
-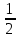 . .
1.
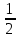 . .
-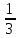 . .
Егер Z=ylnx болса, 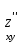 -ті есепте: -ті есепте:
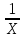
Y
X
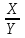
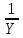
z=f(х,у) функцияның х бойынша дербес туындысы деп аталады:
∆х→0 ұмтылғанда функцияның х бойынша дербес өсімшесінің х аргументтің өсімшесіне қатынасының шегін айтады, бұл жағдайда қалған аргумент өзгеріссіз қалады.
∆х→0 ұмтылғанда функцияның х бойынша дербес өсімшесінің у аргументтің өсімшесіне қатынасының шегін айтады.
∆у→0 ұмтылғанда функцияның у бойынша дербес өсімшесінің у аргументтің өсімшесіне қатынасының шегін айтады, бұл жағдайда қалған аргумент өзгеріссіз қалады.
∆у→0 ұмтылғанда функцияның у бойынша дербес өсімшесінің х аргументтің өсімшесіне қатынасының шегін айтады.
∆х→0 ұмтылғанда функцияның у бойынша дербес өсімшесінің х аргументтің өсімшесіне қатынасының шегін айтады, бұл жағдайда қалған аргумент өзгеріссіз қалады.
Егер 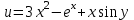 болса, болса, 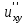 -ті есепте: -ті есепте:
|
 Скачать 0.95 Mb.
Скачать 0.95 Mb.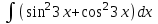
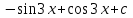
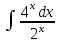
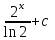
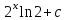
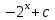
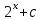
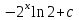
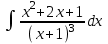
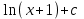
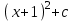
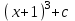
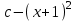
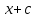
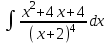
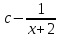
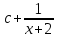
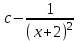
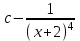
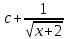
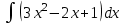
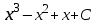
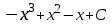
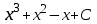
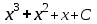
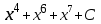
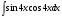
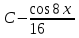
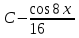
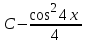
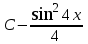
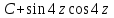
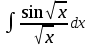
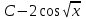
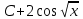
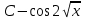
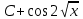
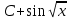
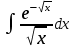
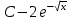
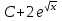
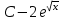
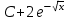
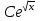
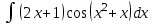
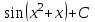
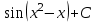
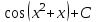
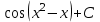
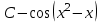
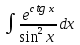
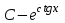
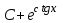
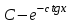
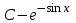
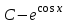
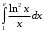 :
: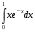 :
: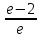
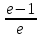
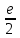
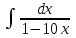 .
. 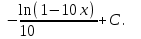
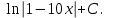
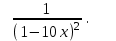
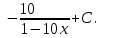
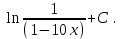
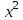 сызықтарымен шектелген фигураның ауданын тап:
сызықтарымен шектелген фигураның ауданын тап: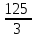
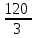
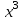 сызықтарымен шектелген фигураның ауданын тап:
сызықтарымен шектелген фигураның ауданын тап: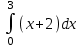 :
: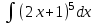 :
: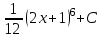
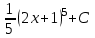
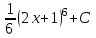
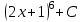
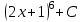 .
.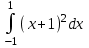 :
: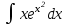 .
. 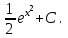
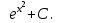
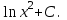
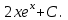
 :
: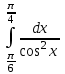 :
: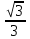 .
. 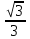 .
. 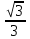
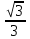
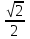 .
.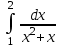 :
: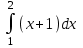 :
: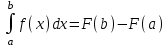
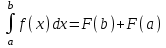
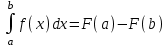
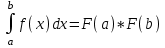
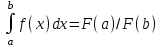
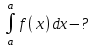
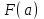
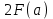
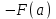
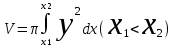
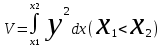
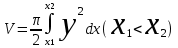
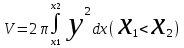
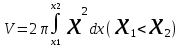
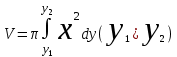
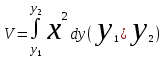
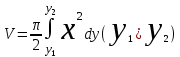
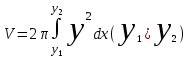
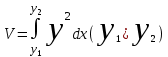
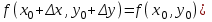 болса, онда
болса, онда 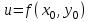 функциясы
функциясы 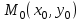 нүктесінде … болады:
нүктесінде … болады: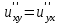
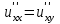
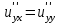
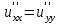
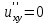
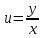 болса,
болса, 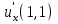 - ті есепте:
- ті есепте: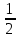 .
. 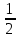
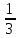 .
.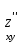 -ті есепте:
-ті есепте: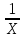
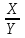
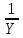
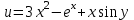 болса,
болса, 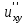 -ті есепте:
-ті есепте: 